基于一维数据逐段均匀条件下的参考分布研究*

张乃今， 张正军， 赵慧秀

(南京理工大学 理学院，南京 210094)

0 引 言

聚类分析是对样本观测值聚集分类的一种探索性分析，其基本思想是通过在研究对象在特征空间上的差异等方面依据相应指标对对象进行分类。虽然无法解释样本观测值分类的合理性，但可以解决很多实际问题，因此仍被广泛应用[1-3]。现如今已经产生很多种估计最佳聚类数的方法[4-7]， 2000年Hastie等提出了Gap Statistic(GS)方法，方法在k-means算法的基础上解决了其他聚类方法无法将数据分成一类的问题。随后几年，学者们在类内离散度的表示、参考分布的选取等方面对GS 方法进行了改进，或将其他方法结合起来处理问题[8-11]。

GS方法引入了一个参考分布，用Gap统计量刻画参考分布下样本观察值与期望值之间的差异，从统计角度解释了样本数据分类的合理性。由此可以看出，选择合适的参考分布对于GS方法十分重要。目前已经理论证明出在一维情况且成员(类)的分布函数形式(退化分布除外)为对数凹的情况下[12]，应选取均匀分布作为参考分布，但对于其他条件下的分布没有相关理论证明。

对此，提出在非对数凹及一维逐段均匀的条件下研究GS方法的参考分布。应用k-means算法对数据进行聚类，假设聚类后的数据是逐段均匀分布，计算不同聚类数下的类内平方和，在给定条件下通过理论证明在这种情况下，总体均匀分布仍是使得类内平方和最大的情况。

1 逐段均匀条件下参考分布研究

在样本容量为p的情况下，对不同分布的数据空间，采用k-means聚类算法分别对其进行聚类，假设每一簇数据都是均匀分布。对于一维数据，总体均匀分布是类内平方和最大的情况。

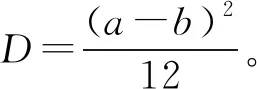
因此，在[0,1]区间上，

(2) 当k=n,n=2,3,…,p时，

设在[0,a1]区间上P(X∈I1)=α1，

在[a1,a1+a2]区间上P(X∈I2)=α2,

⋮

在[a1+a2+…+an-1,1]区间上P(X∈In)=1-α1-α2-…-αn-1=αn。令an=1-a1-a2-…-an-1，如图1所示。

图1 一维情况Fig.1 One-dimensional situation

则有

(1)

用Lagrange乘数法对其求极值，设

(2)

解方程组：

(3)

可以看出，当α1a1=α2a2=…=αnan=-6λ时,Dn(α1,α2,…,αn,a1,a2,…,an)取极值。此时

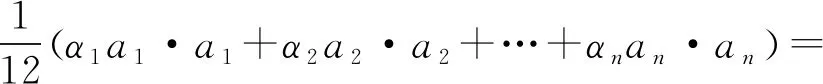
(4)

已知

α1+α2+…+αn-1=1,a1+a2+…+an-1=1

故

(5)

由均值不等式可知

(6)

所以

(7)

则

(8)

即

(9)

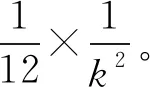
2 实证分析

应用k-means算法，选择了不同的数据集进行聚类，并计算分成各类后的类内平方和。从图2-图7中可以看出，不管各数据集聚类后的类内平方和logWk随着k值怎样变化，这6种数据集的类内平方和均小于总体均匀分布时的类内平方和。说明假设是合理的。

图2 iris数据集 图3 glass数据集 图4 seeds数据集
Fig.2 irisdata set Fig.3 glass data set Fig.4 seeds data set

图5 balance数据集 图6 haberman数据集 图7 wine数据集
Fig.5 balance data set Fig.6 haberman data set Fig.7 wine data set

3 结束语

聚类分析能够获得数据的分布状况，观察每一簇数据的特征，集中对具有相似特征的数据做进一步处理，还可以作为其他算法的预处理步骤。GS方法从统计角度解释了样本数据分类的合理性，补充了聚类分析在分类准确性方面的不足。对于GS方法来说，选择合适的参考分布至关重要。