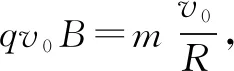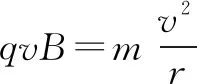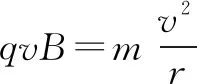巧借边界“相切” 突破高考难点
——例析带电粒子在磁场中的轨迹圆或磁区极值问题
邹韩仕
(广东省汕头市澄海苏北中学 515829)
“带电粒子在磁场中的运动”是历年高考中的一个高频考点,而“带电粒子在有界磁场中运动”的极值问题则是此考点中的一个难点.粒子在磁场中的运动轨迹可能是一个完整的圆或一段圆弧,而有界磁场可以有一个、二个或三个边界,磁区也可以是矩形、正方形、圆形、三角形、环形等.粒子在有界磁场中运动时,也往往会涉及到求轨迹圆最大值(最小值)或磁区最小面积等多类极值问题.尽管此类问题思维容量大,对学生的数学能力、空间想象能力要求也比较高,但通过挖掘问题本质,寻求问题的思维共性,就能得以有效解决.本文拟例析如何利用轨迹圆与磁场边界“相切”这一基本特点,突破带电粒子在有界磁场中运动时出现的轨迹圆或磁区极值问题这一难点,进而提出解决问题的有效策略.
一、凸现一个“模型”
带电粒子在磁场中的运动的轨迹“模型”就是一个“圆”,这个“圆”灵活多变,可平移,可缩放,可旋转,处理问题时可视实际需要进行灵活变通.
二、抓住一条“主线”
定圆心、画轨迹、找半径;找临界(如粒子运动时轨迹恰好与某一磁场边界相切或恰好离开边界上某点);再利用几何关系(通常要在直角三角形中构建半径和给定的几何量之间的几何关系)求半径,是解决此类问题的一条主线.
三、明确一个“关键”
圆心的确定,是解决问题的“关键”.定圆心通常有以下三种方法:
(1)半径相交法:已知入射方向和出射方向时,可通过入射点和出射点作垂直于入射方向和出射方向的直线,两条直线的交点就是圆弧轨道的圆心(如图1中P为入射点,M为出射点).

(2)中垂线法:已知入射方向和出射点的位置,可以通过入射点作入射方向的垂线,连接入射点和出射点,作其中垂线,这两条垂线的交点就是圆弧轨道的圆心(如图2中P为入射点,M为出射点).
(3)角平分线法:若已知粒子入射方向和出射方向,及轨迹半径R,但不知粒子的运动轨迹,则可作出此两速度方向夹角的平分线,在角平分线上与两速度方向直线的距离为R的点即为圆心(此法多用在粒子在有界磁场中运动时轨迹与边界相切,但“切点”不确定的情况).带电粒子在匀强磁场中的圆周运动具有对称性,应用对称性可以快速地确定运动的轨迹.
①带电粒子如果从一直线边界进入又从该边界射出,则其轨迹关于入射点和出射点线段的中垂线对称,入射速度方向、出射速度方向与边界的夹角相等;
② 在圆形磁场区域内,沿径向射入的粒子,必沿径向射出.
四、把握一个“联结点”

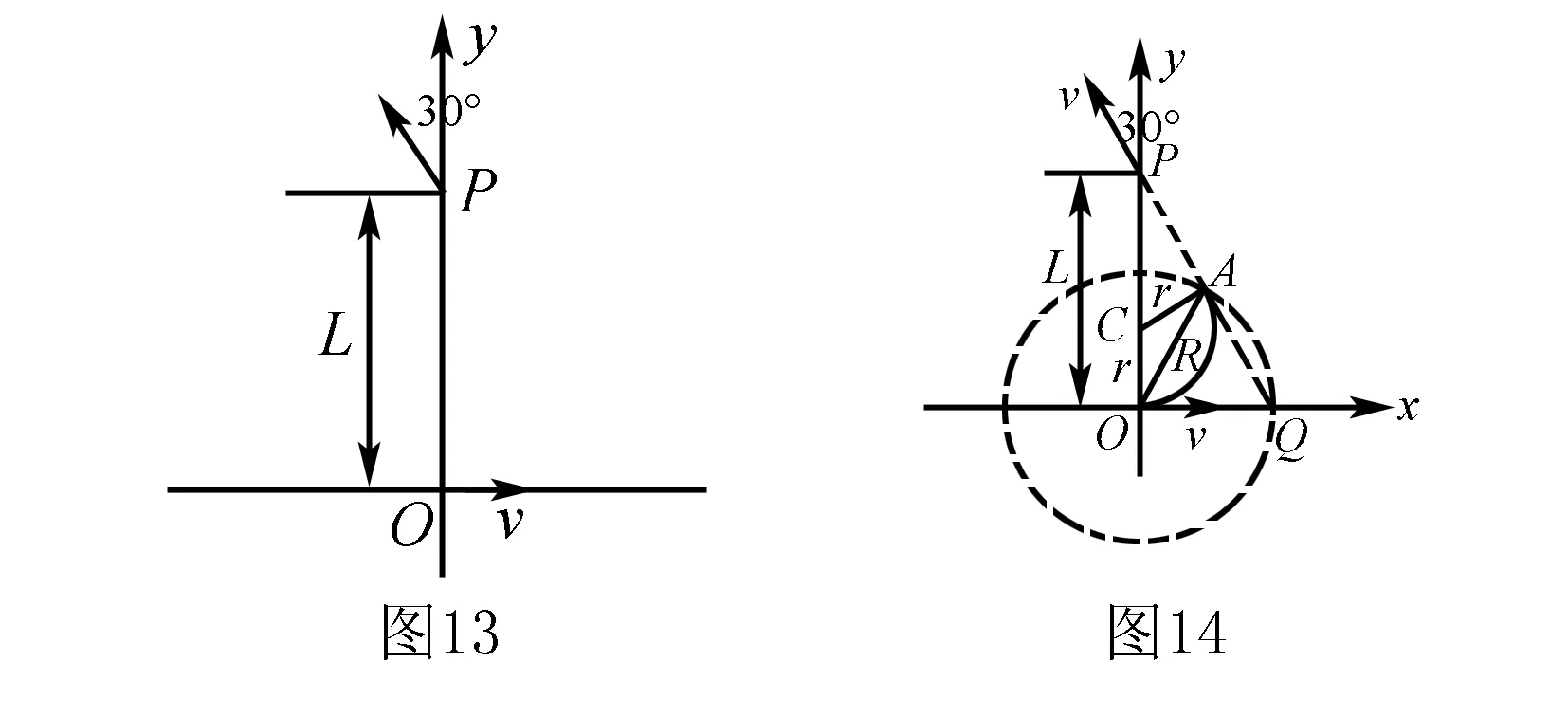
五、带电粒子在磁场中运动出现轨迹圆或磁区极值问题分析
1.磁场区域已知,求轨迹圆的相关极值问题
情境1 磁区为带状
例1如图3所示,匀强磁场的磁感应强度为B,宽度为d,边界为CD和EF.一电子从CD边界外侧以速率v0垂直匀强磁场射入,入射方向与CD边界间夹角为θ.已知电子的质量为m,电荷量为e,为使电子能从磁场的另一侧EF射出,求电子的速率v0至少多大?

解析当入射速率v0很小时,电子会在磁场中转动一段圆弧后又从CD一侧射出,速率越大,轨道半径越大,当轨道的边界与EF相切时,电子恰好不能从EF射出,如图4所示.电子恰好射出时,由几何知识可得:
r+rcosθ=d①

由①②得:

情境2 磁区为矩形

例2一足够长的矩形区域abcd内充满磁感应强度为B、方向垂直纸面向里的匀强磁场,矩形区域的左边界ad长为L,现从ad中点O垂直于磁场射入一速度方向与ad边夹角为30°、大小为v0的带正电粒子,如图5所示.已知粒子电荷量为q,质量为m(重力不计):若要求粒子能从ab边射出磁场,v0应满足什么条件?
解析当粒子轨迹恰好与cd边相切时,是粒子能从ab边射出磁场区域时轨迹圆半径最大的情况,设此半径为R1,如图6所示.则有
可得:R1=L
当粒子轨迹恰好与ab相切时是粒子能从ab边射出磁场区域时轨迹圆半径最小的情况,设此半径为R2,如图7所示


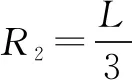
故粒子从ab边射出的条件为R2 情境3 磁区为三角形 例3如图8所示,在一底边长2L,θ=45°的等腰三角形区域内(O为底边中点)有垂直纸面向外的匀强磁场.现有一质量为m,电量为q的带正电粒子从静止开始经过电势差为U的电场加速后,从O点垂直于AB进入磁场,不计重力与空气阻力的影响.则: 磁感应强度B为多少时,粒子能以最大的圆周半径偏转后打到OA板? 解析粒子经电场加速射入磁场时的速度为v,则 如图9,要使圆周半径最大,则粒子的圆周轨迹应与直角边AC边恰好相切,设圆周半径为R 由洛仑兹力提供向心力: 情境4 磁区为环形 例4如图10所示,在以O为圆心,内外半径分别为R1和R2的圆环区域内,存在辐射状电场和垂直纸面的匀强磁场,内外圆间的电势差U为常量,R1=R0,R2=3R0.一电荷量为+q,质量为m的粒子从内圆上的A点进入该区域,不计重力.则:图11中,若粒子从A点进入磁场,速度大小为υ3,方向不确定,要使粒子一定能够从外圆射出,磁感应强度应小于多少? 思维共性:在磁场区域已知时,不管有界磁区为何种形状,解决问题的突破口在于:把握粒子可缩放而出现最大或最小轨迹圆与磁场边界 “相切”这一关键临界信息.例1、例2虽为求带电粒子v0的极值,例3、例4虽为求磁感应强度B的极值,但本质上、方法上是相同的,最终都应转化为求轨迹圆半径的极值. 2.磁场区域未知,而轨迹圆(圆弧)已知,求“约束”磁区的最小面积 情境1 磁区为圆形 例5一匀强磁场,磁场方向垂直于xy平面,在xy平面上,磁场分布在以O为中心的一个圆形区域内.一个质量为m、电荷量为q的带电粒子,由原点O开始运动,初速为v,方向沿x正方向.后来,粒子经过y轴上的P点,此时速度方向与y轴的夹角为30°,P到O的距离为L,如图13所示.不计重力的影响.求磁场的磁感强度B的大小和xy平面上磁场区域的最小半径R. 解析粒子在磁场中受洛仑兹力作用,作匀速圆周运动,设其半径为r, 据此并由题意知,粒子在磁场中的轨迹的圆心C必在y轴上,且P点在磁场区之外.过P沿速度方向作延长线,它与x轴相交于Q点.作圆弧过O点与x轴相切,并且与PQ相切,切点A即为粒子离开磁场区的地点.这样也求得轨迹圆的圆心C,如图14所示. 由图中几何关系得L=3r② 情境2 磁区为三角形 例6如图15所示,在倾角为30°的斜面OA的左侧有一竖直档板,其上有一小孔P,现有一质量m=4×10-20kg,带电量q=+2×10-14C的粒子,从小孔以速度v=3×104m/s水平射向磁感应强度B=0.2T、方向垂直纸面向里的一正三角形区域.该粒子在运动过程中始终不碰及竖直档板,且在飞出磁场区域后能垂直打在OA面上,粒子重力不计.求:正三角形磁场区域的最小边长. 解析如图16当粒子的运动轨迹与正三角形磁场区域的ac边和ab边都相切时,正三角形磁场区域的面积最小.由几何关系可得最小边长为L,即 Lcos30°=r+2rcos30° ① 由牛顿第二定律可得 则粒子在磁场中做圆周运动的半径 联立①②③得L=0.946 m 情境3 磁区为矩形 例7如图17,为可测定比荷的某装置的简化示意图,在第一象限区域内有垂直于纸面向里的匀强磁场,磁感应强度大小B=2.0×10-3T,在X轴上距坐标原点L=0.50 m的P处为离子的入射口,在Y上安放接收器,现将一带正电荷的粒子以v=3.5×104m/s的速率从P处射入磁场,若粒子在y轴上距坐标原点L=0.50 m的M处被观测到,且运动轨迹半径恰好最小,设带电粒子的质量为m,电量为q,不计其重力.则: 为了在M处观测到按题设条件运动的上述粒子,在第一象限内的磁场可以局限在一个矩形区域内,求此矩形磁场区域的最小面积,并在图中画出该矩形. 解析如图18,当轨迹圆与矩形磁区的边界刚好“相切”是矩形磁场区域出现“最小面积”的临界条件,所求的最小矩形是MM1P1P,该区域面积 S=2r2① 联立①②并代入数据得S=0.25m2 矩形如图18中MM1P1P(虚线) 思维共性:求磁区圆的最小面积,关键是先定好轨迹圆半径的圆心(需用角平分线法).不管有界磁区为何种形状,此三类磁场区域出现“最小面积”的情况均有异曲同工之妙:轨迹圆与磁区的边界刚好“相切”是磁场区域出现“最小面积”的临界条件,具有“最小面积”的磁区(圆、三角形或矩形等)将轨迹圆“约束”起来. 带电粒子在磁场中运动时出现轨迹圆最大值(最小值)或磁区最小面积等多类极值问题,教学中需要教师及时帮助学生进行比较分类、分析归纳,通过抓住“圆”这一基本物理模型,提炼问题共性,即不管是磁区已知求轨迹圆大小极值,或轨迹圆可求进而求磁区面积极值,都有轨迹圆与磁区边界“相切”这一明显临界特征.画好圆,找出边界“切点”,再结合几何关系求解轨迹圆半径这一重要联结点,进而视问题情况进行适当的参数转换,则问题能迎刃而解.