临近空间飞行器的鲁棒控制器设计

王 鉴，赵宏宇，钟继鸿，王孟渝，蔡志俊

(上海机电工程研究所，上海 201109)

0 引 言

近几年来，临近空间飞行器的战略价值引起了世界各国的重视，同时也因其显著的优点和军民两用的潜在价值而成为研究热点。但从整体发展水平看，临近空间飞行器的广泛应用目前仍处于关键技术攻关阶段。

临近空间飞行器具有发射平台多样、飞行速度快、可机动、多弹道变化、突防能力强和能够打击时间敏感目标等突出优势，对传统的防空反导防护体系提出了严峻的挑战。

临近空间飞行器的飞行高度和马赫数跨度范围较大，气动特性变化剧烈，且无法预知飞行扰动[1]。为解决这一问题，尝试采用H∞混合灵敏度鲁棒控制方法，引入加权函数，由加权函数直接反映系统的各项性能指标，研究被控对象的鲁棒性，同时验证系统的性能改善情况。

1 混合灵敏度控制思想

飞行器的不确定性反馈控制系统结构如图1所示。

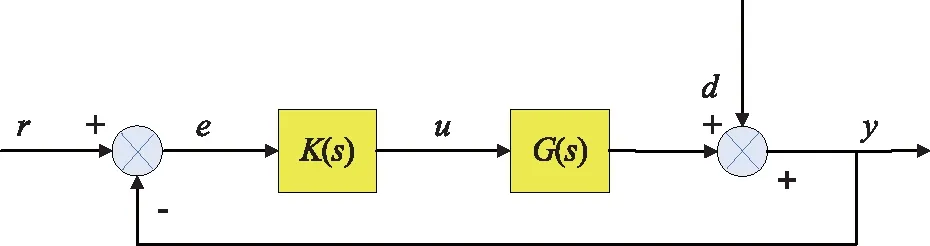
图1 飞行器不确定性反馈控制系统结构Fig.1 Structure of flight vehicle’s uncertainty feedback control system

式中：r、e、u、d和y分别是被控系统的外部输入、误差信号、控制器输出、外部扰动输入和被控系统的输出的测量值；G(s)为被控对象；K(s)为所设计的H∞混合灵敏度鲁棒控制器。

定义灵敏度函数S(s)为

(1)

式中：S(s)是干扰d与输出y以及误差e与输入r之间的闭环传递函数。S(s)越小，系统的干扰抑制能力越强，系统的跟踪误差越小。

定义补灵敏度函数T(s)为

(2)

由于T(s)制约系统输出信号的大小，因此，T(s)决定系统鲁棒稳定性[2]。

综上，为了使被控制系统具备鲁棒性，且可抑制干扰输入和精确跟踪指令信号，希望控制系统的S(s)奇异值和T(s)奇异值能够同时达到最小。

由于扰动具有低频特性，模型不确定性往往是由于忽略高频特性引起的，因此可在不同频段设计S(s)和T(s)。引入性能加权函数WS(s)、控制器输出加权函数WR(s)和鲁棒加权函数WT(s)，并修改飞行器的不确定性反馈控制系统为标准H∞控制结构，如图2所示。

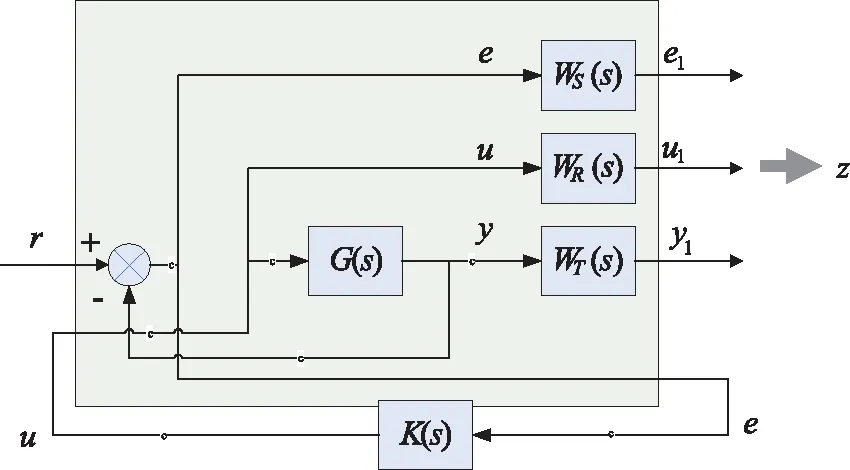
图2 标准控制结构Fig.2 Standard control structure

图2中，z是被控制的输出；e1、u1、y1分别为e、u、y被控制的输出。

则系统从输入r到输出z的传递函数为

(3)

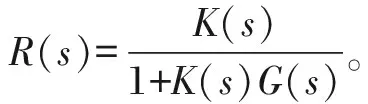
H∞混合灵敏度最优控制问题的本质为：设计控制器K(s)，使被控对象系统稳定，并且满足Tzr<γ(γ为系统的性能指标)，提高系统性能。

2 纵向H∞混合灵敏度鲁棒控制器设计

2.1 飞行器纵向运动方程

以某型临近空间飞行器为被控对象，通过求取飞行器在给定高度和飞行速度的平衡状态，在平衡点对其数学模型进行小扰动线性化处理，并忽略机体和舵面下洗的动力系数小量，得到飞行器空中飞行的纵向短周期运动的状态空间方程为[3]

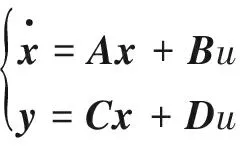
(4)

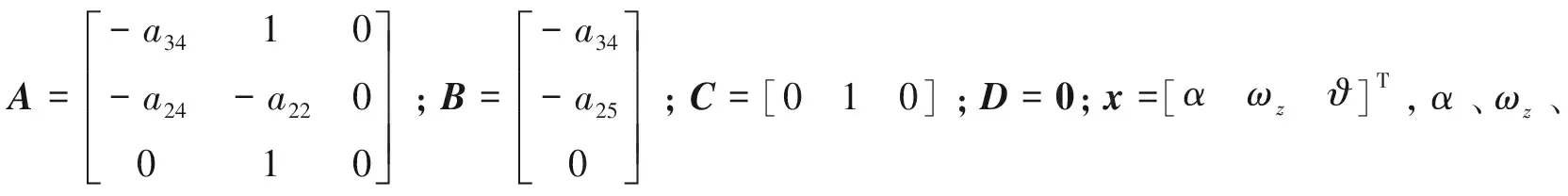
2.2 纵向H∞混合灵敏度鲁棒控制器设计

纵向控制器的首要任务是保证飞行器精确跟踪整个飞行基准弹道。

临近空间飞行器的飞行包线宽广，气动特性变化剧烈，是复杂的时变不确定性系统，其不确定性包括：模型的动态特性偏差、大包线内的飞行参数剧烈变化以及大气扰动等不确定性干扰。采用H∞混合灵敏度鲁棒控制方法，引入加权函数，使得被控系统具备鲁棒性和较高的系统性能，可快速跟踪指令信号，有效抑制各项不确定性干扰。

基于实际情况，如果在高度回路设计鲁棒控制器，将会导致系统纵向控制器的阶次过高，不符合实际工程应用需求。因此，在俯仰角回路采用H∞混合灵敏度鲁棒控制设计方法。为了使系统稳定，并且降低控制器阶次，采用比例法设计系统的增稳回路。

俯仰角回路H∞混合灵敏度鲁棒控制器的设计结构如图3所示[4]。

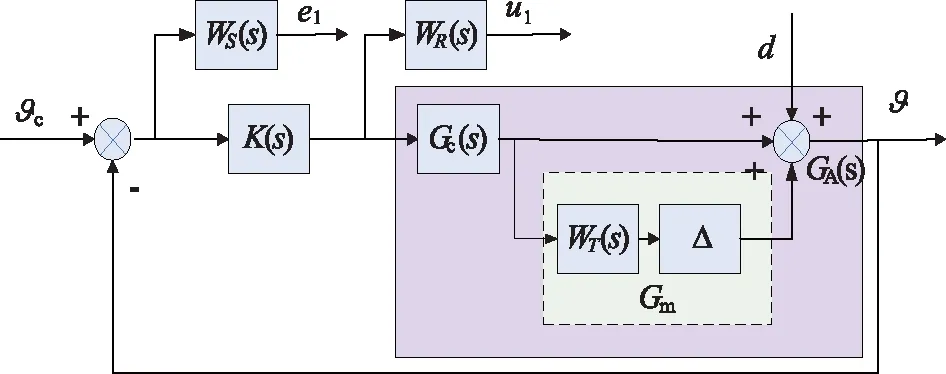
图3 H∞混合灵敏度鲁棒控制器的结构Fig.3 Structural block diagram of mixed sensitivity robust controller

图3中：ϑc为输入俯仰角指令；Gc(s)为标称控制对象；GA(s)为实际控制对象；Gm为非结构型输出端不确定性模型；d为外界干扰输入；ϑ为回路实际俯仰角输出。

增加角速度和攻角内反馈回路作为系统的增稳回路，控制模型不确定的范围。

在保证系统稳定性的

前提下，降低系统纵向控制器的阶次。最终设计的标称控制对象Gc(s)如图4所示。

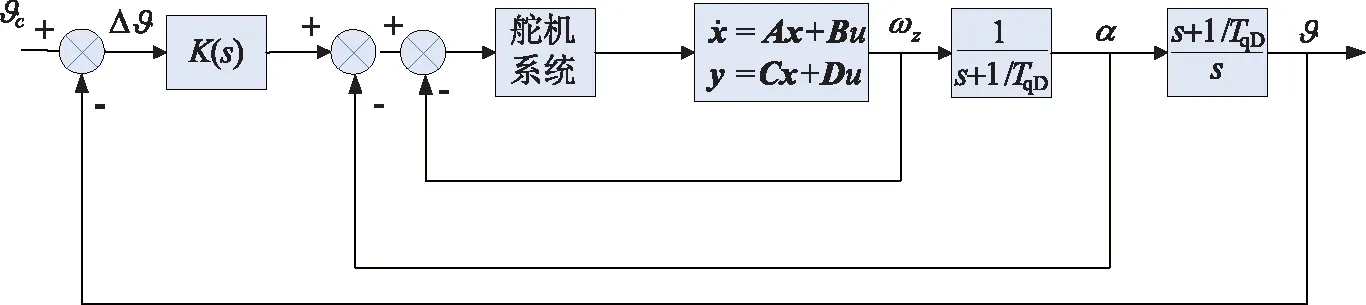
图4 标称控制对象Gc(s)结构Fig.4 Block diagram of nominal control object Gc(s)

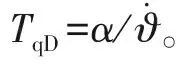
2.3 选取标称控制对象

标称控制对象的选取过程为：首先，分析飞行器的飞行包线并选定合适的特征点；其次，绘制特征点处数学模型的奇异值Bode图，选取奇异值居中的那个特征点作为标称控制对象[5]。

某型临近空间飞行器从0Ma开始加速爬升，当飞行速度为4Ma时进行高空巡航飞行[6]。由于飞行器在加速爬升阶段的飞行高度和飞行马赫数跨度范围较大，气动特性变化剧烈。为此，选取加速爬升阶段的6个飞行状态作为特征点，设计纵向通道的H∞混合灵敏度鲁棒控制器。所选取的6个特征点的飞行状态如表1所示。

表1 6个飞行状态特征点Tab.1 Six flight state characteristic points

绘制选定特征点的奇异值 Bode 图，如图5所示。

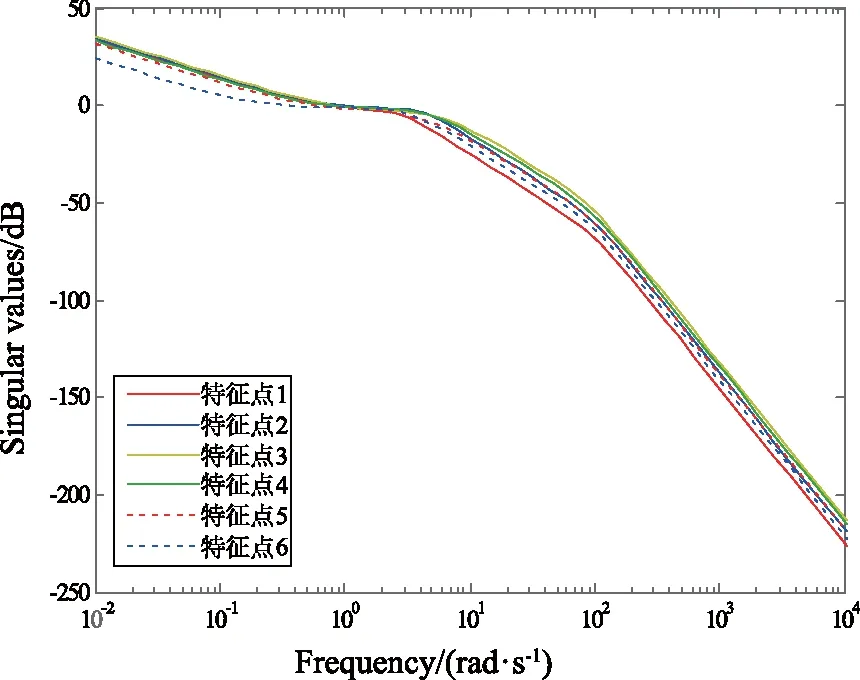
图5 选定的6个特征点的奇异值Bode图Fig.5 Singular value Bode graphs of six selected characteristic points

由图5可以看出，虽然6个特征点的曲线规律类似，但是飞行器的空域跨度较大，综合衡量，选取特征点4(Ma=1.5，H=10 km)所对应的状态空间模型作为标称控制对象，进行H∞混合灵敏度鲁棒控制器的设计分析。

2.4 选取加权函数

H∞混合灵敏度鲁棒控制器设计的本质是由加权函数直接反映系统的各项性能指标要求。当选定标称控制对象后，加权函数的选取就成为设计控制器至关重要的一步，合理的加权函数可以提高系统的动态品质、系统鲁棒性以及系统的抗干扰能力等。

1) 设计性能加权函数WS(s)

WS(s)是对灵敏度函数S(s)的加权函数，根据系统性能的要求而选取。WS(s)应具有积分特性或者高增益低通特性，以增强对干扰的抑制能力。在低频段，WS(s)的增益值应尽量大，以使S(s)尽量小，这样可以有效抑制干扰的影响或精确地跟踪输入信号。在高频段，为了使被控系统的超调量在一定的范围内，宜将WS(s)的幅值设置在0.1～0.8区间范围内，此时对应的S(s)的增益为0 dB，且在全频域范围内，S(s)的最大奇异值小于WS-1(s)的最大奇异值[7]。

本文在保证系统鲁棒稳定的前提下，设计的性能加权函数为

(5)

在Matlab/Simulink中绘制WS-1(s)和S(s)的奇异值特性曲线，如图6所示。

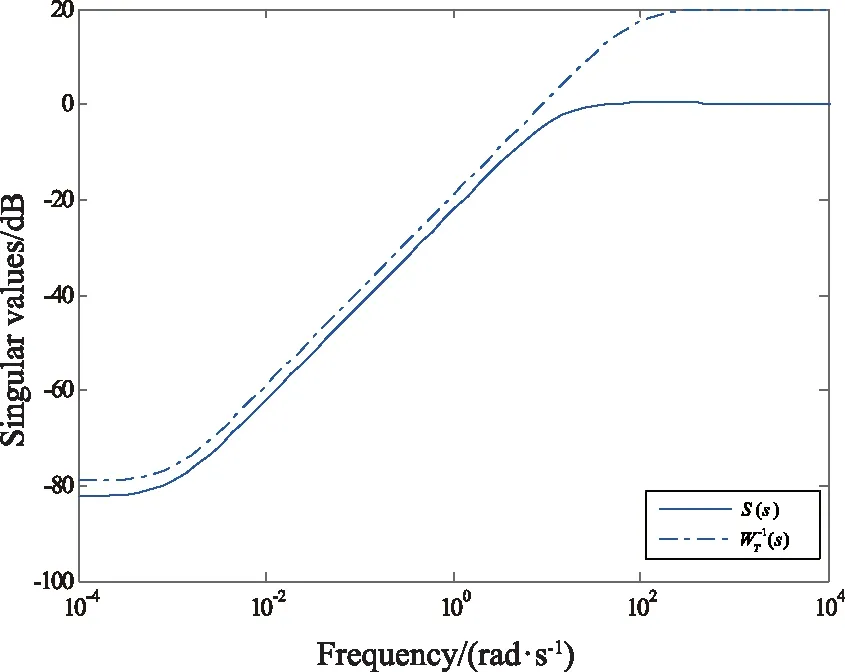
图6 WS-1(s)和S(s)的奇异值特性曲线Fig.6 Singular value characteristic curve of WS-1(s) and S(s)

由图6可知，灵敏度函数S(s)的最大奇异值在全频域内小于WS-1(s)的最大奇异值，设计的WS(s)满足性能加权函数的设计要求。

2) 选取鲁棒加权函数WT(s)

WT(s)是对补灵敏度函数T(s)的加权函数，代表乘性摄动的范数界，反映系统对鲁棒稳定性要求，即系统高频性能需求。因此，在高频段，选取具有高通特性的WT(s)函数，以消除模型不确定性的影响。此外，为了抑制高频干扰的影响，WT(s)应具备较大的高频段增益及较小的低频段增益。在低频段，模型参数变化引起的等效模型误差的最大奇异值应大于WT(s)的最大奇异值。

模型不确定性用输出端乘性不确定性表示时，Gc(s)和Gci(s)的关系为

Gci(s)=(I+Gmi(s))Gc(s)

(6)

即

Gmi(s)=(Gci(s)-Gc(s))Gc-1(s)

(7)

式中：i=1,2,3,5,6；Gc(s)为标称控制对象数学模型；Gci(s)为其他特征点数学模型；Gmi(s)为非结构型输出端不确定型模型；I为单位矩阵。

对标准控制对象Gc(s)选取加权函数WT(s)时，首先，根据WT(s)的最大奇异值与模型参数变化引起的等效模型误差的最大奇异值的关系，初步设计鲁棒加权函数WT(s)，即计算选定的特征点处Gmi(s)的奇异值，并保证在有效频段内Gmi(s)的最大奇异值大于WT(s)的最大奇异值。然后，在高频段，为了抑制高频干扰的影响，WT(s)的高频增益应尽量高，并结合实际情况，选取低阶次的WT(s)。

设计的鲁棒加权函数为

(8)

在Matlab/Simulink中绘制非结构型输出端不确定型模型Gmi(s)的奇异值与WT(s)的奇异值的关系，如图 7所示。

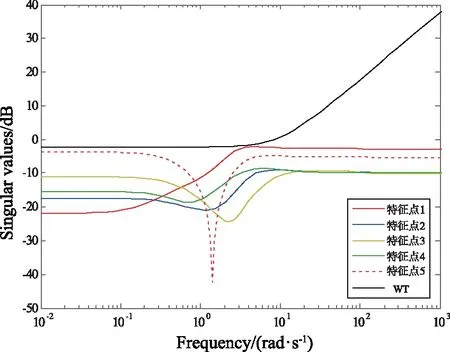
图7 Gmi(s)与WT(s)的奇异值关系图Fig.7 Singular value relation diagram of Gmi(s)and WT(s)

由图7可知，设计的WT(s)满足非结构型输出端不确定型模型的设计要求。此外，绘制WT-1(s)和T(s)的奇异值特性曲线，如图8所示。

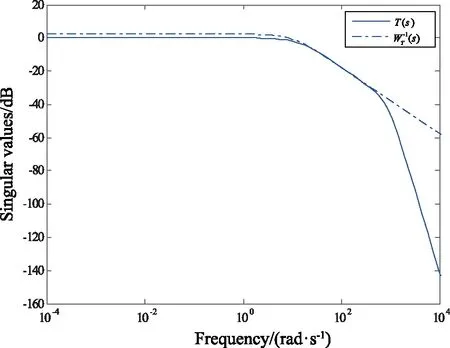
图8 WT-1(s)和T(s)的奇异值特性曲线Fig.8 Singular values characteristic curvesof WT-1(s) and T(s)

由图8可知，补灵敏度函数T(s)的最大奇异值在全频域内小于WT-1(s)的幅值，满足设计要求，并且灵敏度函数WT-1(s)的最大奇异值在全频域内小于T(s)的最大奇异值，证明选取的加权函数在保证系统鲁棒性的情况下可使系统的性能最优化。

3) 选取控制器输出加权函数WR(s)

为了使设计的控制器具备工程意义，防止控制器的输出过大，需引入控制器输出加权函数WR(s)以限制控制量的大小。此外，引入WR(s)还应保证系统具有足够的带宽。通常，WR(s)选为一个合适的常数形式。

本文中，控制器输出加权函数取值为

WR(s)=0.000 1

(9)

选定加权函数后，以标称控制对象为纵向控制器设计对象，通过Matlab的鲁棒控制工具箱的augtf及hinfsyn函数设计H∞混合灵敏度鲁棒控制器[8]。根据混合灵敏度H∞次优控制理论，设计的H∞混合灵敏度鲁棒控制器为

(10)

3 鲁棒控制器性能仿真验证

为了进一步验证设计的H∞混合灵敏度鲁棒控制器的性能指标，采用某型临近空间飞行器的线性化模型进行性能仿真验证。

利用Matlab软件，仿真验证在H∞混合灵敏度鲁棒控制器的控制下某型临近空间飞行器在6个选定特征点的时域频域响应特性。

1) 时域响应特性验证

各特征点的单位阶跃响应如图9所示。在H∞混合灵敏度鲁棒控制器的控制下，系统在选定特征点处的时域响应特性良好，超调量较小，上升时间较短，响应较快。

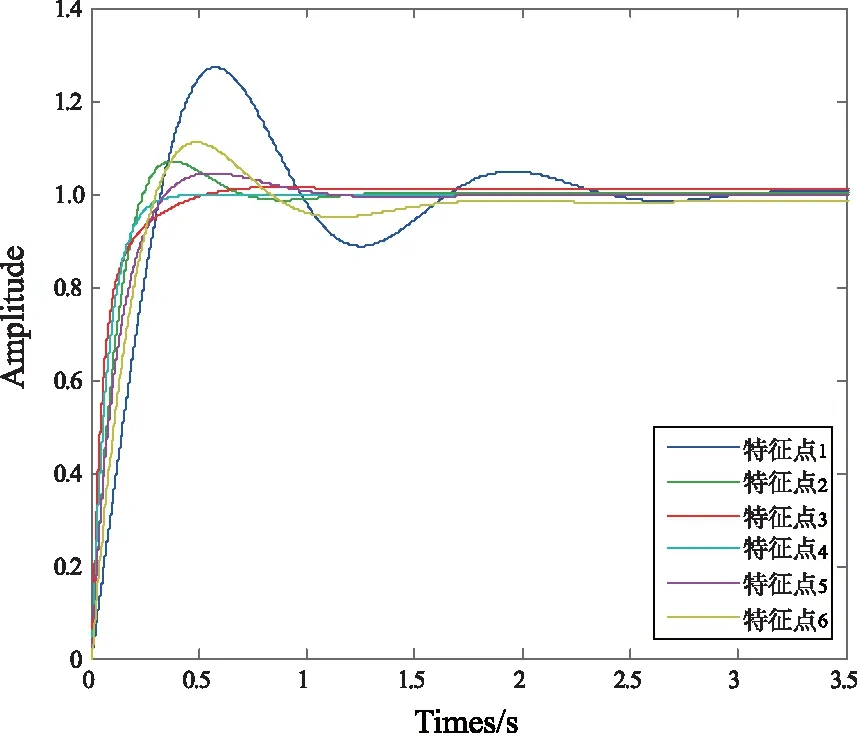
图9 各特征点的单位阶跃响应Fig.9 Unit step response of each characteristic point

2) 频域响应特性验证

各特征点的频域响应如图10～15所示。

(1) 特征点1(Ma=0.5，α=3°)

由图10可知，幅值裕度γ=43.6 dB(频率F=471 rad·s-1)，相角裕度h=42.2°(F=5.11 rad·s-1)。

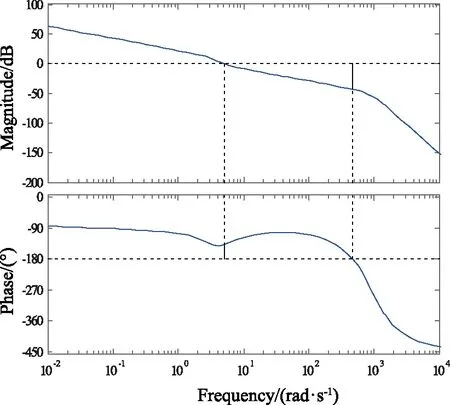
图10 特征点1频域响应曲线Fig.10 Frequency domain response curve of characteristic point 1

(2) 特征点2(Ma=0.8，α=0°)

由图11可知，γ=35.8 dB(F=471 rad·s-1)，h=73.8°(F=9.29 rad·s-1)。

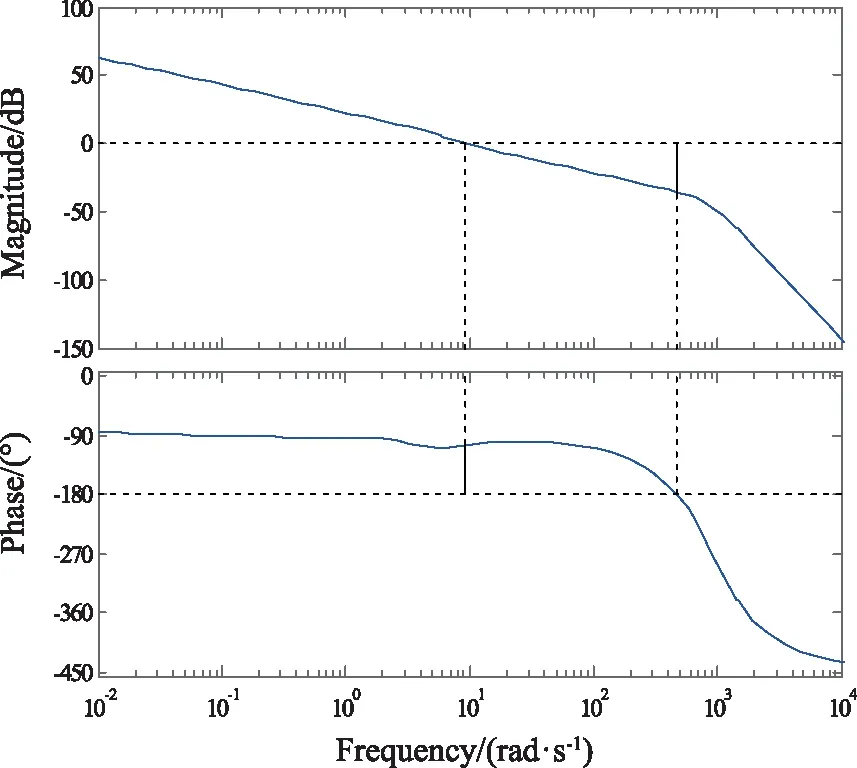
图11 特征点2频域响应曲线Fig.11 Frequency domain response curve of characteristic point 2

(3) 特征点3(Ma=1.2，α=0°)

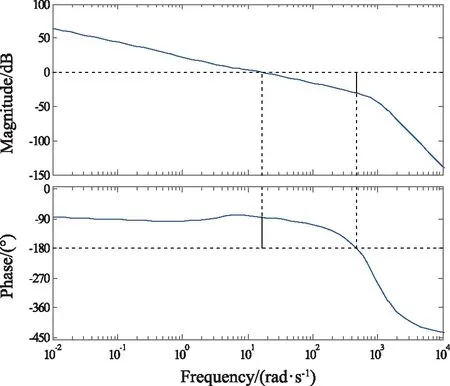
图12 特征点3频域响应曲线Fig.12 Frequency domain response curve of characteristic point 3

由图12可知，γ=30.2 dB(F=471 rad·s-1)，h=94.8°(F=16.6 rad·s-1)。

(4) 特征点4(Ma=1.5，α=0°)

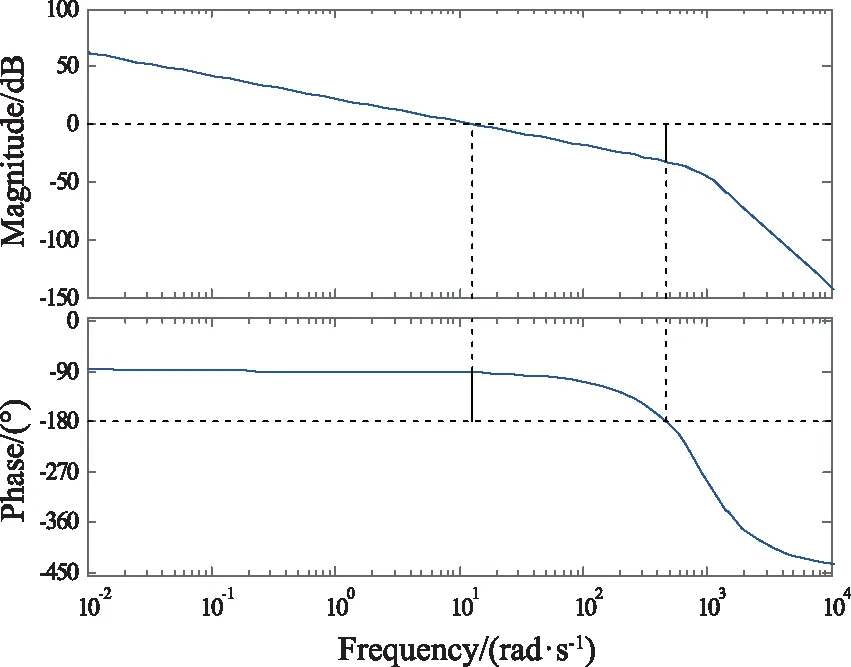
图13 特征点4频域响应曲线Fig.13 Frequency domain response curve of characteristic point 4

由图13可知，γ=32.5 dB(F=471 rad·s-1)，h=87.6°(F=12.9 rad·s-1)。

(5)特征点5(Ma=2，α=3°)

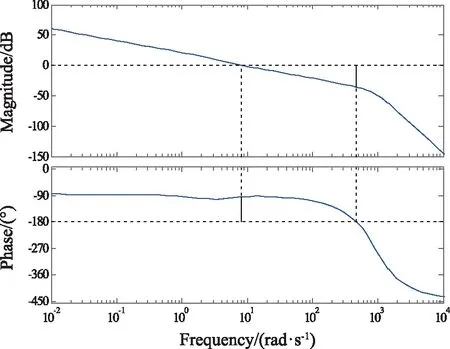
图14 特征点5频域响应曲线图Fig.14 Frequency domain response curve of characteristic point 5

由图14可知，γ=35.8 dB(F=471 rad·s-1)，h=85.1°(F=8.15 rad·s-1)。

(6) 特征点6(Ma=4，α=3°)

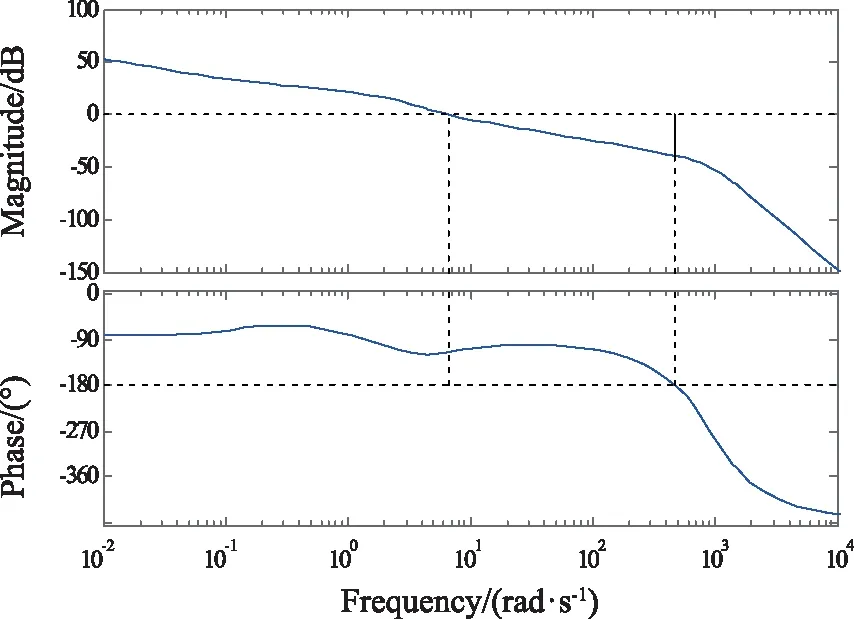
图15 特征点6频域响应曲线图Fig.15 Frequency domain response curve of characteristic point 6

由图15可知，γ=39.2 dB(F=471 rad·s-1)，h=65.6°(F=6.56 rad·s-1)。

由图 10至图 15可知，在H∞混合灵敏度鲁棒控制器的控制下，系统在6个选定的特征点处的频域特性响应良好。幅值裕度大于30 dB，相角裕度基本大于60°，最大可达94.8°，具备较强的鲁棒性。

综上，在所设计的H∞混合灵敏度鲁棒控制器的控制下，某型临近空间飞行器可快速地响应指令信号，并且系统具备较强的鲁棒性，系统的时域频域特性满足工程指标。

4 结束语

本文首先介绍了应用H∞混合灵敏度鲁棒控制的意义及其控制思想；然后，通过选取合适的标称控制对象和设计合理的加权函数，设计了飞行器纵向H∞混合灵敏度鲁棒控制器；最后，仿真验证了飞行器的时域频域响应特性。结果表明，设计的控制器可使被控对象具备良好的时域频域特性，具有很好的工程参考价值。