基于扩张状态观测器的有限时间收敛制导律

陈泽宏,钟继鸿,赵宏宇,王 鉴

(1. 空军驻上海地区第一军事代表室，上海 201109； 2. 上海机电工程研究所，上海 201109)

0 引 言

考虑到导引头测量信息的特点，目前应用最广泛的制导律是比例导引律和修正比例导引律。比例导引律易于实现且导弹具有较好的弹道特性，能满足导引律的基本要求。但是，由于初始误差、导弹速度变化、目标机动等对比例导引律的影响，导弹需用过载变化很大，甚至在弹目接近过程中会出现需用过载过早饱和而导致比例导引性能大大下降，最终脱靶量过大的情况。随着目标的机动性能和速度不断提升，末端制导信息存在不连续变化，经典导引规律的不足日益凸现。随着现代控制理论的发展，许多学者提出了新的现代导引律[1-5]。根据技术指标的要求，在引入性能指标函数基础上利用极小值原理得到的最优制导律，在拦截非机动目标或者小机动目标时能取得良好的制导效果。滑模变结构制导律的设计思想比较简单，在解决参数不确定的非线性控制系统问题的时候有很大优势。许多研究者针对大机动目标设计了变结构导引律，还有类似基于人工智能的制导律、微分对策制导律等。

然而，上述大多数制导律都是基于渐近稳定性或者指数稳定性方法设计的，只有当时间趋于无穷时，视线角速度才会为零，而实际上末制导过程的时间是有限的。同时，在上述制导律设计中往往没有考虑导弹动力学特性的影响，如果考虑制导末端的制导控制回路特性，弹目视线角速度实际上将趋向于发散，导弹需用过载将急剧增大，可能导致制导回路失稳。因此，上述制导律的主要缺点是存在视线角速度收敛时间和稳定控制系统动态响应的问题。基于非线性系统的有限时间稳定性方法，文献[6]提出了一种使视线角速度有限时间收敛的制导律。根据有限时间收敛控制理论，文献[7]应用滑模变结构控制方法设计了一种考虑导弹稳定控制系统二阶动态特性的有限时间收敛导引律。

制导控制回路是探测制导系统与稳定控制系统组成的非线性级联系统，因此反步控制设计方法适用于考虑导弹稳定控制系统动态特性的制导律设计。在末制导中，对制导系统而言，主要的干扰其实是目标的机动和测量噪声。在未考虑稳定控制系统动态特性的制导律中，造成脱靶量变大的最主要原因是导弹加速度响应滞后于制导指令，严重时甚至会使制导回路失稳。 在本文中，为提高闭环制导系统的性能，考虑到稳定控制系统为一阶环节，利用反步设计方法，在进行制导律设计时结合了加速度指令的积分控制，并根据平行接近导引法思想，推导了一种新的有限时间制导律。理论分析证明，该方法能够在弹目交会前使弹目视线角速度收敛到零。为了对目标机动进行有效补偿，本文将扩张状态观测器(extended state observer, ESO)的反步设计应用到有限时间制导律中，对弹目视线角速度的跟踪与目标机动估计问题进行了研究。

1 弹目相对运动模型

为了便于问题分析，考虑平面制导问题，弹目运动示意图如图1所示。在参考坐标系oxz中，导弹(M)与目标(T)之间的连线为视线，视线与ox轴夹角q为视线角，R为弹目相对距离，vM、vT分别为导弹和目标的速度，aMq、aTq分别为导弹和目标垂直于视线的加速度，aMR、aTR分别为导弹和目标沿着视线方向的加速度。

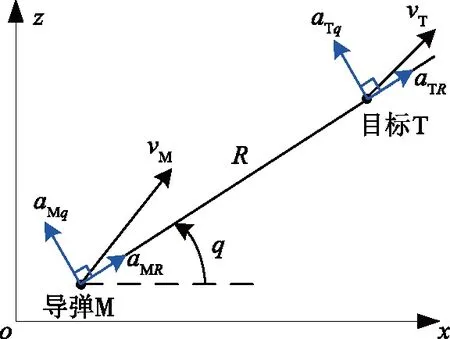
图1 弹目相对运动示意图Fig.1 Schematic diagram of missile-target relative motion

根据图1所示几何关系可得

(1)

实际中导弹响应加速度指令是动态的，因此在本文中考虑导弹稳定控制系统为一阶惯性环节,其表达式为

(2)

式中：τ为加速度响应时常数；u为加速度控制指令。

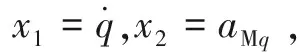
(3)

(4)

2 有限时间收敛制导律

经典飞行力学指出，无论目标进行何种机动飞行，当采用平行接近导引时，导弹需用法向过载总是小于目标机动时的法向过载，这样可减小对导弹机动性能的要求。根据平行接近法思想，在末制导过程中，要求视线角速度尽可能快地收敛到零。

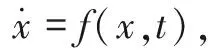
(5)

本文利用反步设计方法，有限时间收敛制导律设计分为以下3个部分内容。

2.1 制导控制回路指令设计

导引头可测得弹目视线角速度，然后通过制导指令形成装置产生导弹加速度指令。根据平行接近法，设计的制导指令应使得式(3)有限时间稳定，即x1→0。对此有如下定理。

定理1：若设计的虚拟制导指令x2c为

(6)

(7)

将式(6)代入式(7)得

(8)

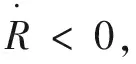
由此可得

(9)

2.2 稳定控制回路指令设计

设计加速度控制指令u，使得x2有限时间跟踪上x2c。在式(4)中取状态反馈控制为

u=τk+x2

(10)

式中：k为待设计的控制量。

由于存在导弹加速度动态响应过程，x2与x2c存在误差，即跟踪误差。定义加速度跟踪误差e=x2-x2c，则有

(11)

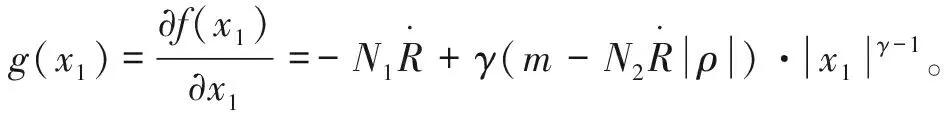
将式(3)代入到式(11)可得

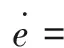
(12)

将x2=e+x2c代入式(3)可得

(13)

定理2：对于式(12)和式(13)，若取控制量k为

(14)

则加速度跟踪误差e和弹目视线角速度x1有限时间收敛到零。

证明：选取新的Lyapunov函数为V2=V1+|e|，则有

(15)

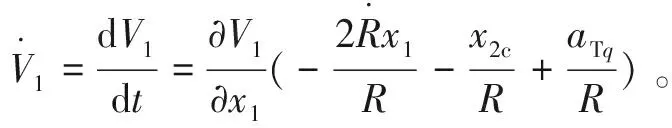
(16)

将式(14)代入式(12)，并整理可得

(17)

则有

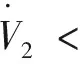
(18)

由于δ>‖aTq‖且g(x1)>0，R>0，则有并且所以由式(18)可得

(19)

对于任意常数p、x、y，当p≥1时有(|x|+|y|)1/p≤|x|1/p+|y|1/p成立，则由式(19)可得

(20)

根据引理1可知，弹目视线角速度x1和加速度跟踪误差e有限时间收敛到零。

2.3 基于ESO的制导控制回路指令设计与实现

由式(6)可得

(21)

将式(3)代入式(21)可得

(22)

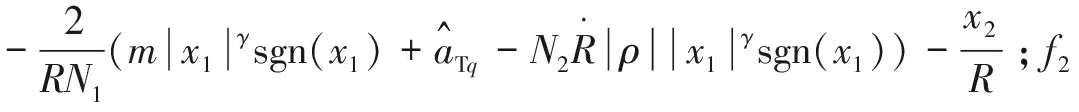
对式(22)设计ESO可得

(23)

式中：

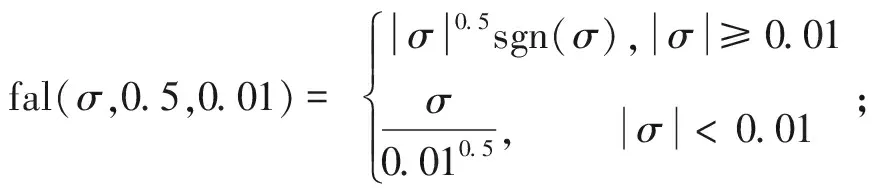
z1跟踪弹目视线角速度x1；z2跟踪系统模型的干扰项与未知部分f2。由此可得弹目视线角速度估计和目标机动估计值。由此可得

(24)

式中：ω1=(f1(z1,x2)+z2)/b+ω。同理，对式(24)设计ESO可得

(25)

式中：x1c为期望弹目视线转动角速度，令x1c=0以实现平行接近导引；z3跟踪控制量ω1。由此可得，基于ESO的有限时间收敛制导指令为

(26)

3 仿真验证

在末制导段考虑导引头测量噪声进行仿真。假设导弹加速度响应时常数为τ=0.4 s，初始位置为xM(0)=4 000 m、zM(0)=500 m，速度vM=1 000 m/s。目标初始位置为xT(0)=16 000 m、zT(0)=3 500 m，速度vT=800 m/s。假定导弹初始弹道偏角指向目标。导弹可用加速度为400 m/s2。仿真中，目标飞行方式分别设为平飞和aT=100 sin(2πt/5) m/s2的正弦机动，并在相同的初始条件下与增强型比例导引(augmented proportional navigation，APN)方法进行对比。

1) 目标平飞

弹目视线角速度和导弹加速度的仿真结果如图2和图3所示，目标平飞时加速度估计如图6(a)所示，脱靶量见表1。

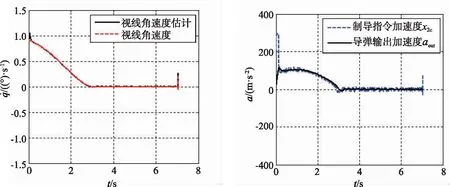
(a) 弹目视线角速度 (b) 加速度指令与输出图2 本文制导律仿真结果Fig.2 Simulation results of guidance law in this paper

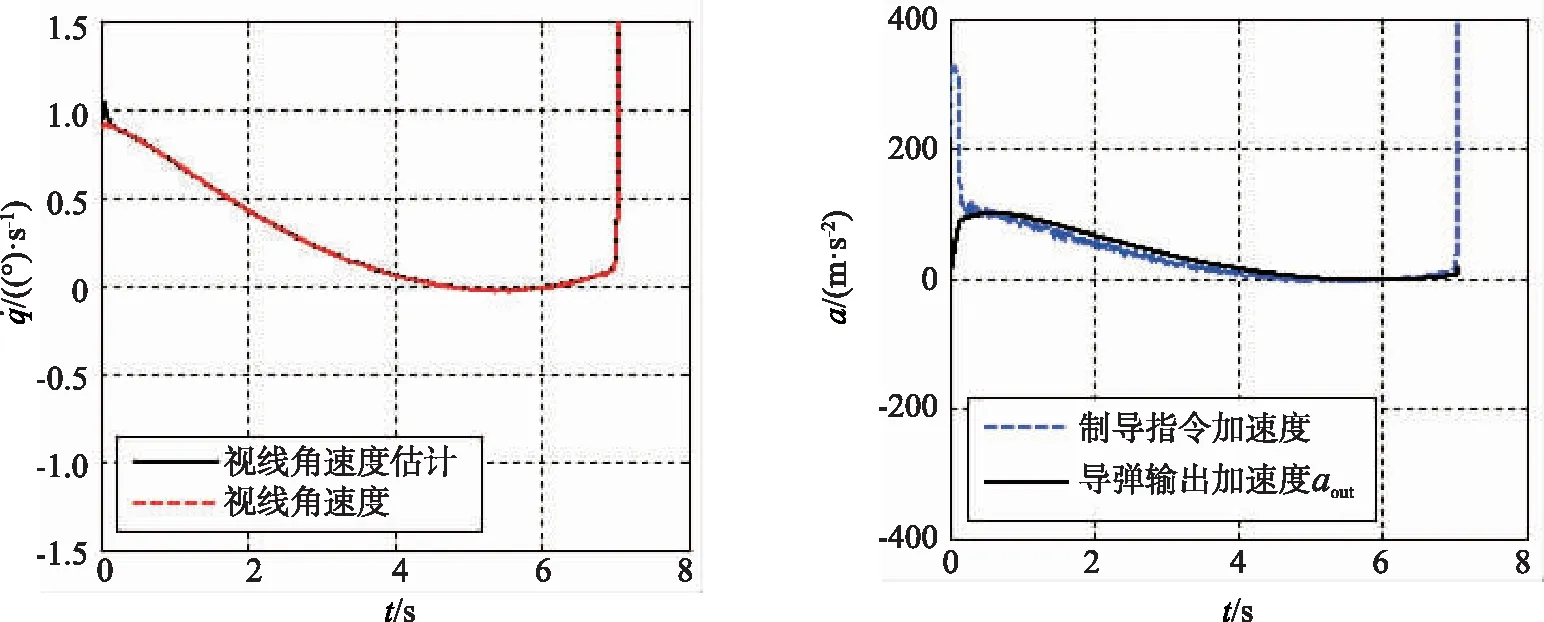
(a) 弹目视线转率 (b) 加速度指令与输出图3 APN制导律仿真结果Fig.3 Simulation results of APN guidance law

2) 目标正弦机动

弹目视线角速度和导弹加速度的仿真结果如图4和图5所示，目标正弦机动时加速度估计如图6(b)所示，脱靶量见表1。

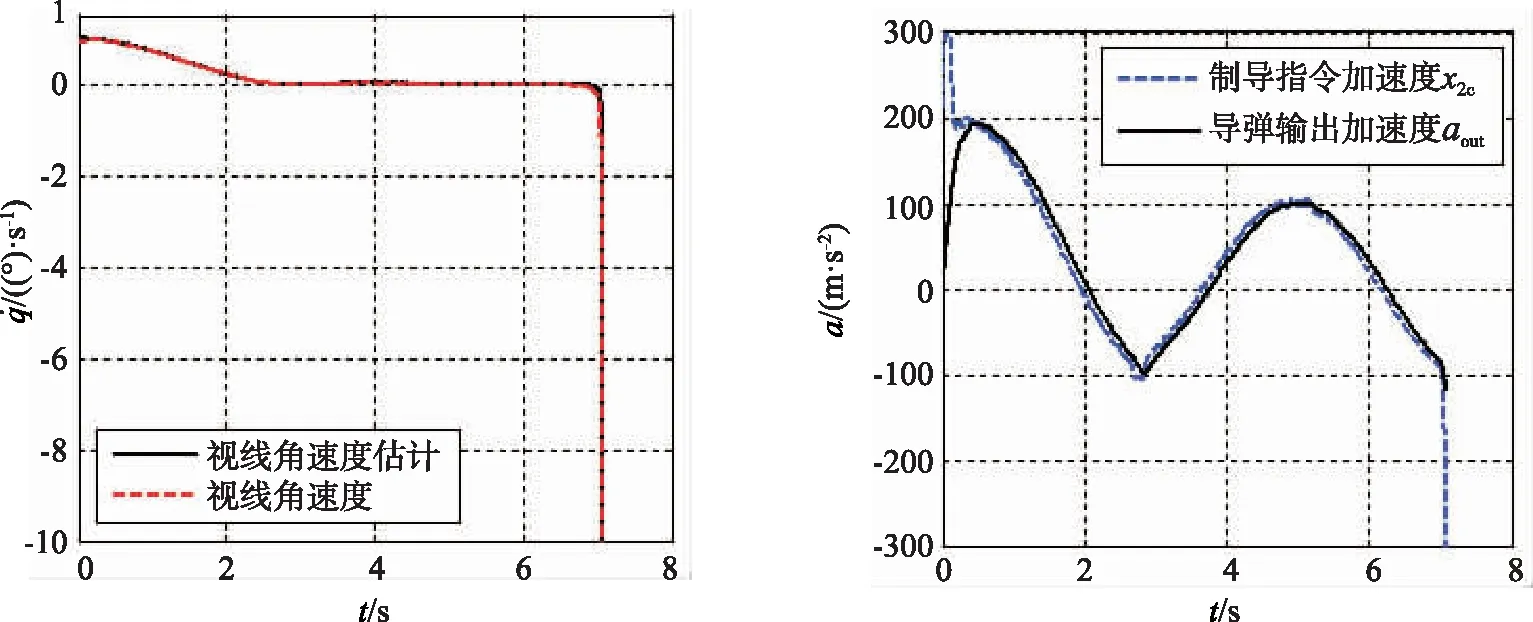
(a) 弹目视线转率 (b) 加速度指令与输出图4 本文制导律仿真结果Fig.4 Simulation results of guidance law in this paper

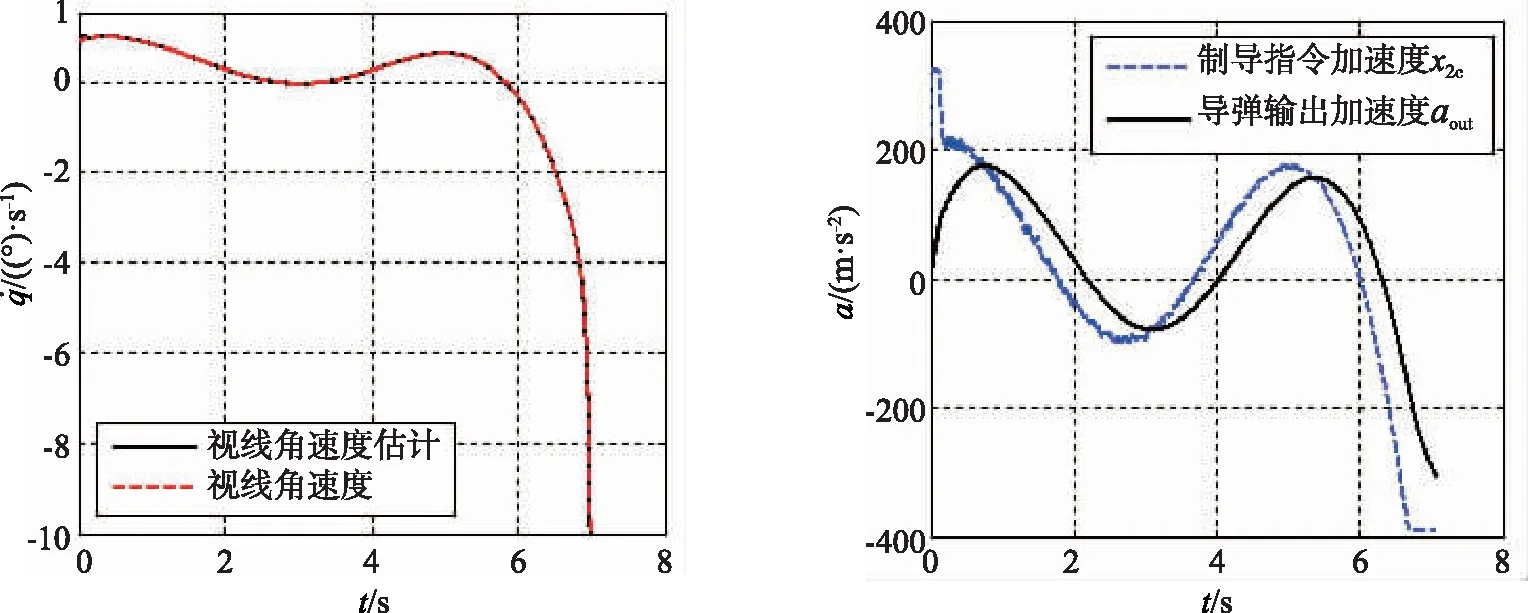
(a) 弹目视线转率 (b) 加速度指令与输出图5 APN制导律仿真结果Fig.5 Simulation results of APN guidance law

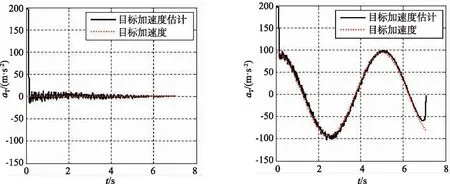
(a) 平飞情况下 (b) 正弦机动情况下图6 基于ESO的目标加速度估计结果Fig.6 Target acceleration estimation based on ESO

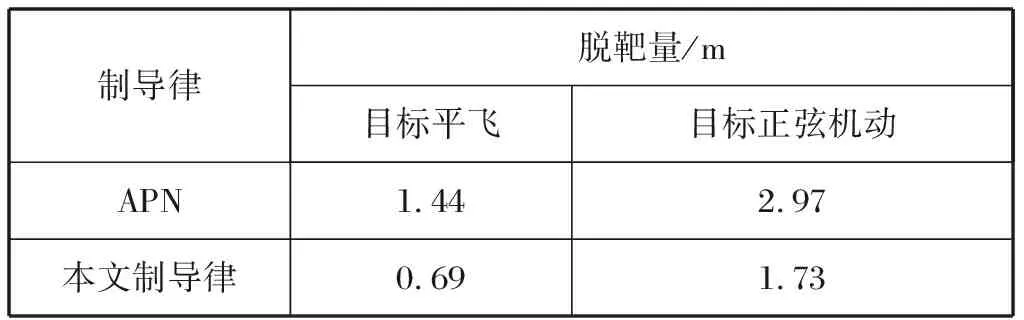
表1 目标平飞和正弦机动情况下的脱靶量Tab.1 Miss Distance when target in level flightand sinusoidal maneuver

图2～5中，(a)图表明：在本文所设计的制导律下，视线角速度能够在有限时间内收敛到零附近；目标正弦机动情况下视线角速度最后才发散，目标平飞情况下视线角速度不发散，所以制导精度较高。由于APN设计过程中忽略了加速度响应延迟，所以平飞和机动情况下视线角速度均较早发散，导致脱靶量较大。

图2～5中，(b)图给出了两种制导律下的加速度指令和导弹加速度的变化过程。可以看出：制导过程开始时，本文所设计制导律下的导弹加速度相对较大，视线角速度能够快速地收敛到零附近；而APN下的导弹初始加速度相对较小，所以视线角速度收敛慢，在目标机动情况下APN末端所需加速度较早被限幅，且加速度响应滞后于指令。从图4(b)中可见导弹输出加速度能够快速准确跟踪加速度指令，这是因为本文在制导律设计中考虑了稳定控制系统的动态特性。

图6给出了采用ESO方法估计得到的目标加速度情况。ESO方法能够快速收敛并准确估计出目标加速度，在末端时弹目距离较近，ESO估计值与实际值的误差变大，因此，在实际应用时弹目交会前0.5 s不再接入目标加速度补偿，以保证制导精度。

4 结束语

本文考虑导弹稳定控制系统的动态特性，通过扩张状态观测器对目标机动进行补偿，设计了一种有限时间收敛制导律。通过理论分析和仿真验证可知，该制导律能够使视线角速度在有限时间内收敛到零附近。与APN相比，本文所设计制导律的加速度跟踪指令滞后小，导弹末端加速度小，制导精度更高，对机动目标具有鲁棒性。