三阱Duffing-Van der Pol系统的分支与混沌

石艳香

(山西大学 数学科学学院, 山西 太原 030006)

0 引言

本文考虑如下带有两个外力项和五次非线性项的三阱Duffing-Van der Pol系统

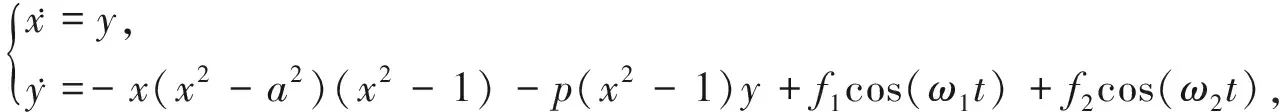
(1)

这里,x表示位移,p>0,00,且ωj>0(j=1,2)是实参数。fj和ωj(j=1,2)分别是两个外力的振幅和频率。

系统(1)本质上等价于Duffing和Van der Pol振子的组合,在非线性振子模型中都具有广泛的应用,其丰富的分支集结构、分支道路、混沌动力学以及锁相现象的研究见[1-6]。 Jing和Wang[7]给出在周期扰动下带有两个外力项的Duffing系统混沌存在的条件。 Jing[8]给出在周期扰动下Duffing-Van der Pol方程产生混沌的条件。 在周期扰动下的三阱Duffing系统的混沌存在标准见Jing[9]。 由同宿或者异宿分支产生的混沌的必要条件由Yang[10]给出。 近年,有关典型振子的混沌动力学有了丰富的研究结果。 Feng[11]用扩展的pade方法研究了非对称非线性动力系统的混沌起始阈值,包括外周期激励下具有阻尼的双阱和三阱系统,建立了Melnikov函数,证明了系统运动是有规律的。 Bala Shunmuga Jothi[12]通过数值分析研究了耦合四阱Duffing-Van der Pol振子的分支与混沌,包括无扰动、单个外力、两个外力、一个外力和有界噪声激励四种情形。 Miwadinou[13]研究了一类化学振子的非线性动力学,该振子是经修正的带有一个外力和三次非线性项的Van der Pol-Duffing振子,利用Melnikov方法分析确定了化学振子中出现混沌的区域边界,研究了约束参数对混沌阈值的影响。 同年,Miwadinou[14]通过Melnikov方法研究了幅值调节力驱动的混合Rayleigh-Liénard振子的混动运动。 Shen[15]基于Melnikov方法研究了具有位移和速度时滞反馈并带有谐波激励的Duffing振子的分支与混沌行为,建立了产生Smale马蹄混沌的必要条件。 目前,国内外文献中对系统(1)的混动动力学研究还较少。

1 非扰动系统的不动点和相图

若p=f1=f2=0,方程组(1)可以写成如下非扰动形式

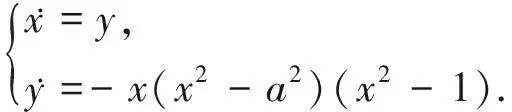
(2)

系统(2)是一个Hamiltonian系统,Hamiltonian函数为

三阱势能函数为

通过对系统(2)不动点(xj,yj)的稳定性分析,可以得到如下结论。

引理[7-9]系统(2)有五个不动点:(0,0),(1,0)和(-1,0)是中心,(a,0)和(-a,0)是鞍点。(a,0)和(-a,0)通过两条异宿轨道连接,(a,0)通过一条同宿轨道连接自身,(-a,0)通过另一条同宿轨道连接自身。

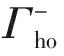
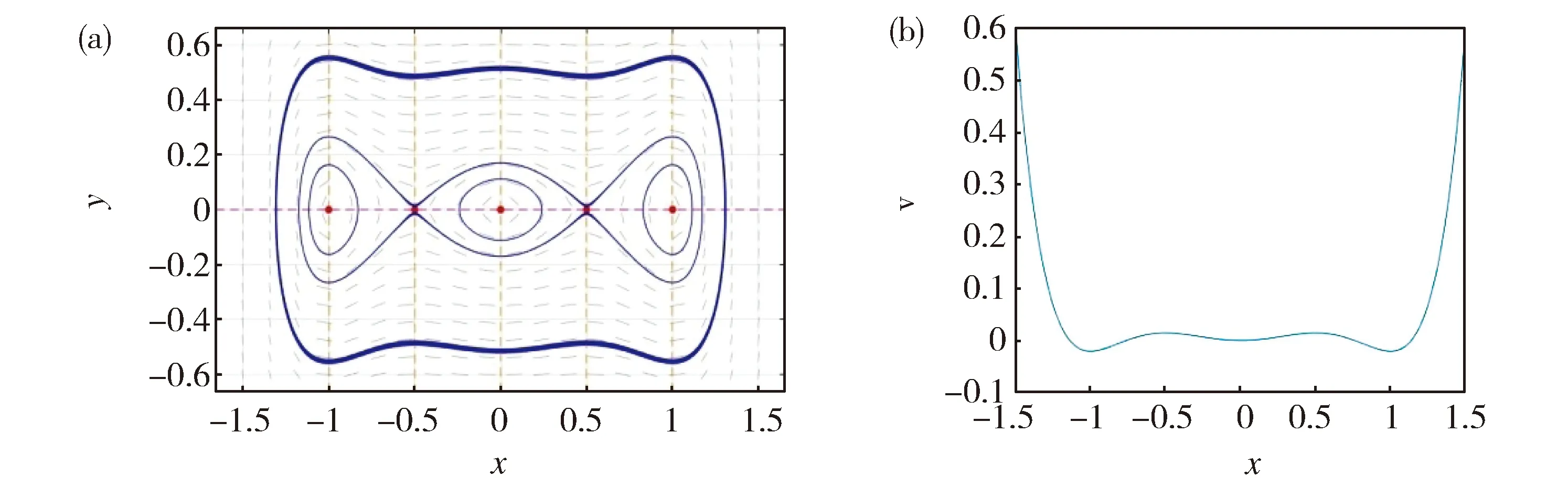
Fig.1 Phase portrait and potential of the system (2) for a=0.5图1 系统(2)的相图和势能图,这里a=0.5

2 周期扰动下系统的混沌

方程组(1)可写成如下自治形式

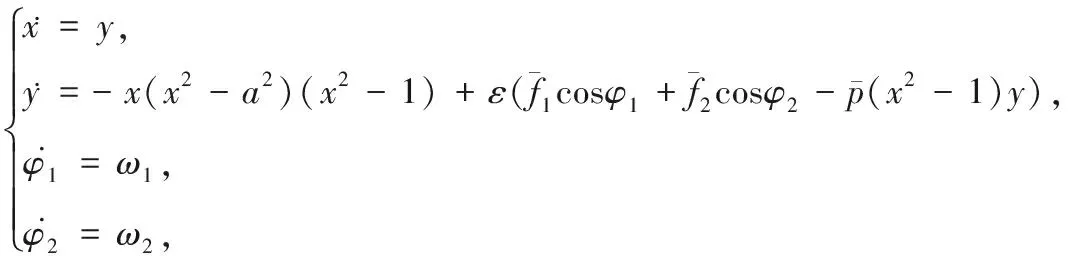
(3)

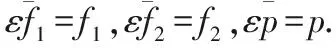
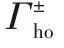
(4)

这里t0是Poincaré映射与横截面相交的时间。

(5)

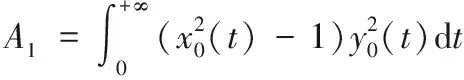
或者

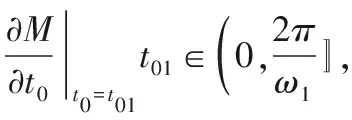
定理1 系统(3)在

p=R1(f1,f2,ω1,ω2)

发生同宿分支,这意味着若ε>0充分小,则横截同宿轨道存在,系统(3)可能产生混沌。

(6)

或者

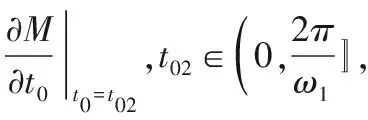
定理2 系统(3)在

p=R2(f1,f2,ω1,ω2)

发生异宿分支,这意味着若ε>0充分小,则横截异宿轨道存在,系统(3)可能产生混沌。

3 数值模拟

本节利用数值模拟来验证上一节所得到的理论结果,同时进一步发现系统新的复杂动态。

计算分支条件(5)和(6)的算法基本上包括两步:用四阶Runge-Kutta方法求解微分方程(2)得到(x0(t),y0(t));求积分得到A1,A2,Ihom1,Ihom2,Ihet1和Ihet2。

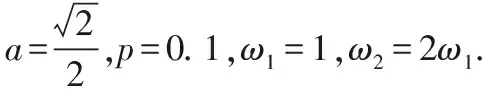
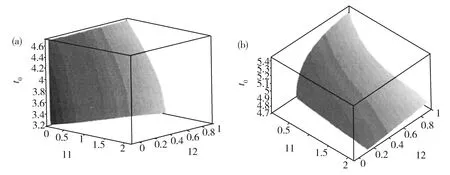
(a) Homoclinic bifurcation curved surface of M(t0)=0(5);(b) Heteroclinic bifurcation curved surface of M(t0)=0(6).Fig.2 Bifurcation curved surface in the (f1,f2,t0) plane for (a)同宿分支曲面M(t0)=0(5);(b)异宿分支曲面M(t0)=0(6)图2 (f1,f2,t0)空间的分支曲面,这里

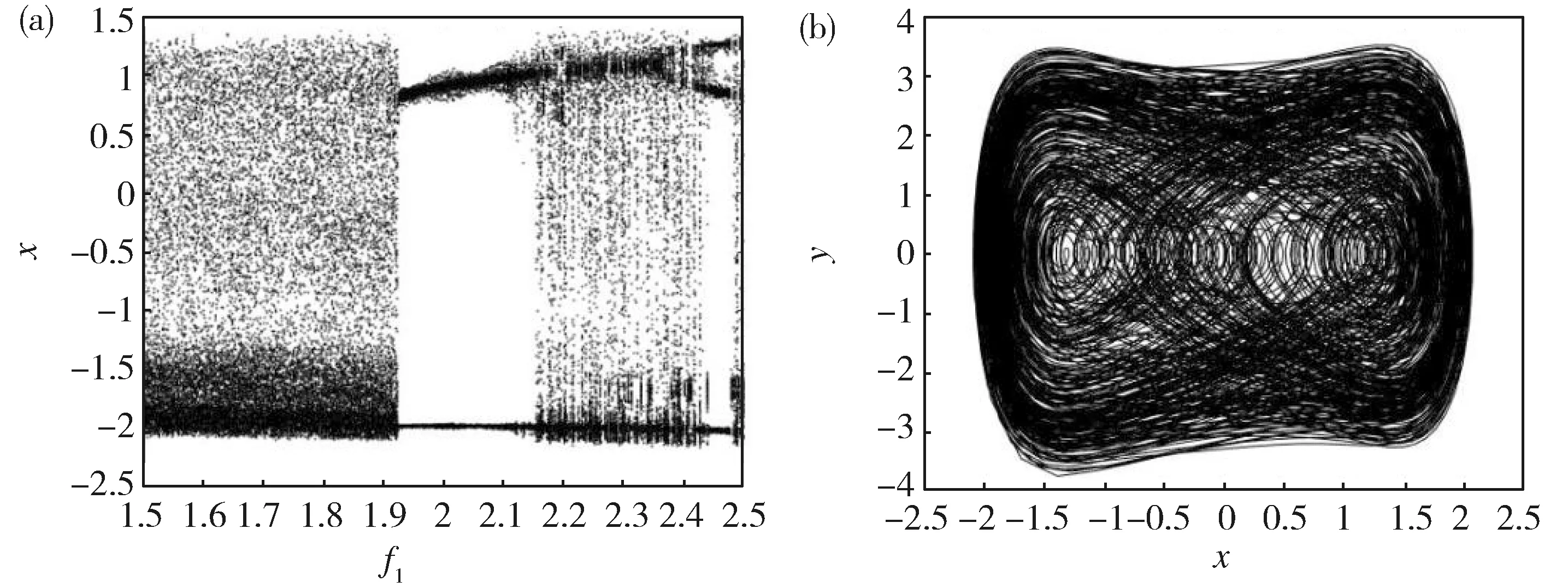
Fig.3 (a)Bifurcation diagram of the system (1) in (f1,x) plane for (b)Phase portrait of the system (1) for f1=1.8图3 (a)系统(1)在(f1,x)平面上的分支图,这里处的相图

接下来,利用数值模拟,研究系统(1)在周期和拟周期扰动下的动态行为。分支参数考虑如下五种情形。

(1)a是分支参数(0≤a≤1),固定p=1,f1=0.1,f2=0.2,ω1=1,ω2=1.5;

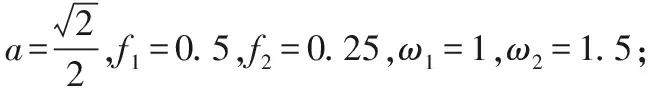
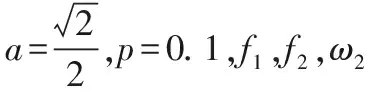
情形(1)图4(a)为系统(1)在(a,x)平面上的分支图。图4(b)给出a=0.5处的相图。

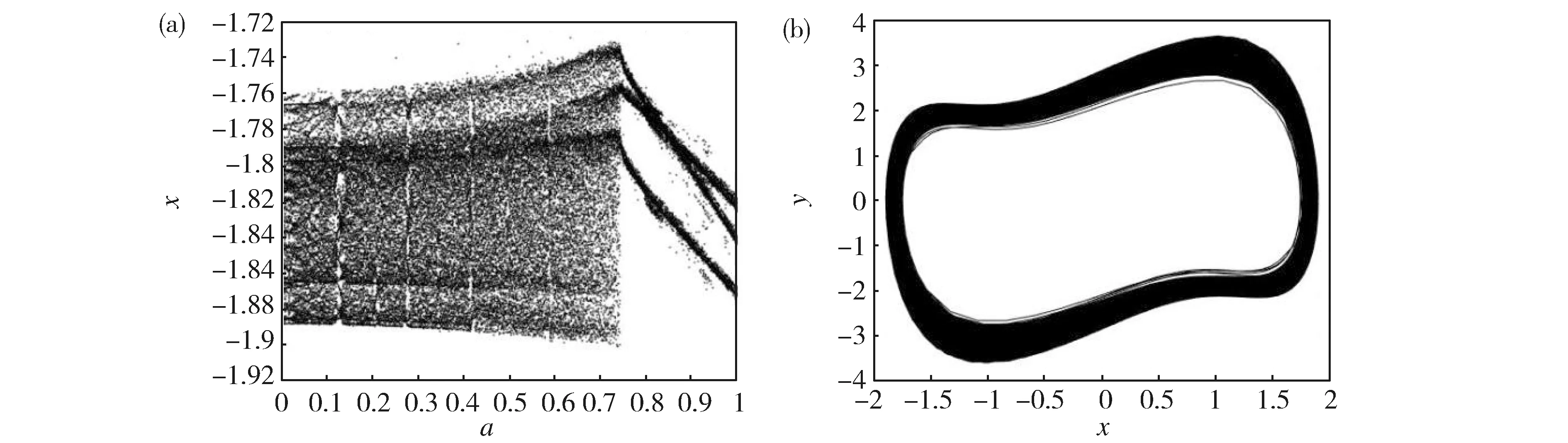
Fig.4 (a)Bifurcation diagram of the system (1) in (a,x) plane for p=1,f1=0.1,f2=0.2,ω1=1,ω2=1.5;(b)Phase portrait of the system (1) for a=0.5图4 (a)系统(1)在(a,x)平面上的分支图,这里p=1,f1=0.1,f2=0.2,ω1=1,ω2=1.5;(b)a=0.5处的相图

情形(2)图5(a)为系统(1)在(p,x)平面上的分支图。从图中可以发现,在p≈1处发生了逆倍周期分支,系统从混沌状态进入周期状态。图5(b)给出p=0.5处的相图。

Fig.5 (a) Bifurcation diagram of the system (1) in (p,x) plane for (b) Phase portrait of the system (1) for p=0.5图5 (a)系统(1)在(p,x)平面上的分支图,这里处的相图

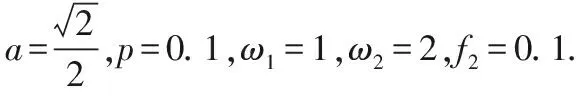
Fig.6 (a) Bifurcation diagram of the system (1) in (f1,x) plane for (b) Amplified bifurcation diagram of (a) in 1.8≤f1≤2.2; (c) Amplified bifurcation diagram of (a) in 2.3≤f1≤2.7;(d) Phase portrait of the system (1) for f1=2.47图6 (a)系统(1)在(f1,x)平面上的分支图,这里(b)对应于(a)在1.8≤f1≤2.2上的局部放大分支图;(c)对应于(a)在2.3≤f1≤2.7上的局部放大分支图;(d)f1=2.47处的相图

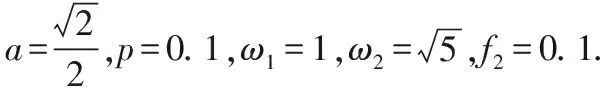
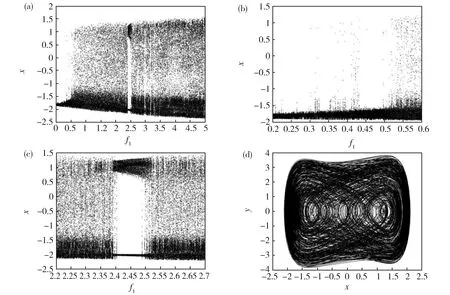
Fig.7 (a)Bifurcation diagram of the system (1) in (f1,x) plane for (b) Amplified bifurcation diagram of (a) in 0.2≤f1≤0.6; (c) Amplified bifurcation diagram of (a) in 2.2≤f1≤2.7;(d) Phase portrait of the system (1) for f1=2图7 (a)系统(1)在(f1,x)平面上的分支图,这里(b)对应于(a)在0.2≤f1≤0.6上的局部放大分支图;(c)对应于(a)在2.2≤f1≤2.7上的局部放大分支图;(d)f1=2处的相图

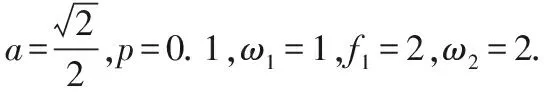
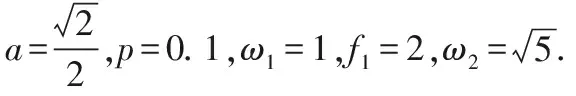
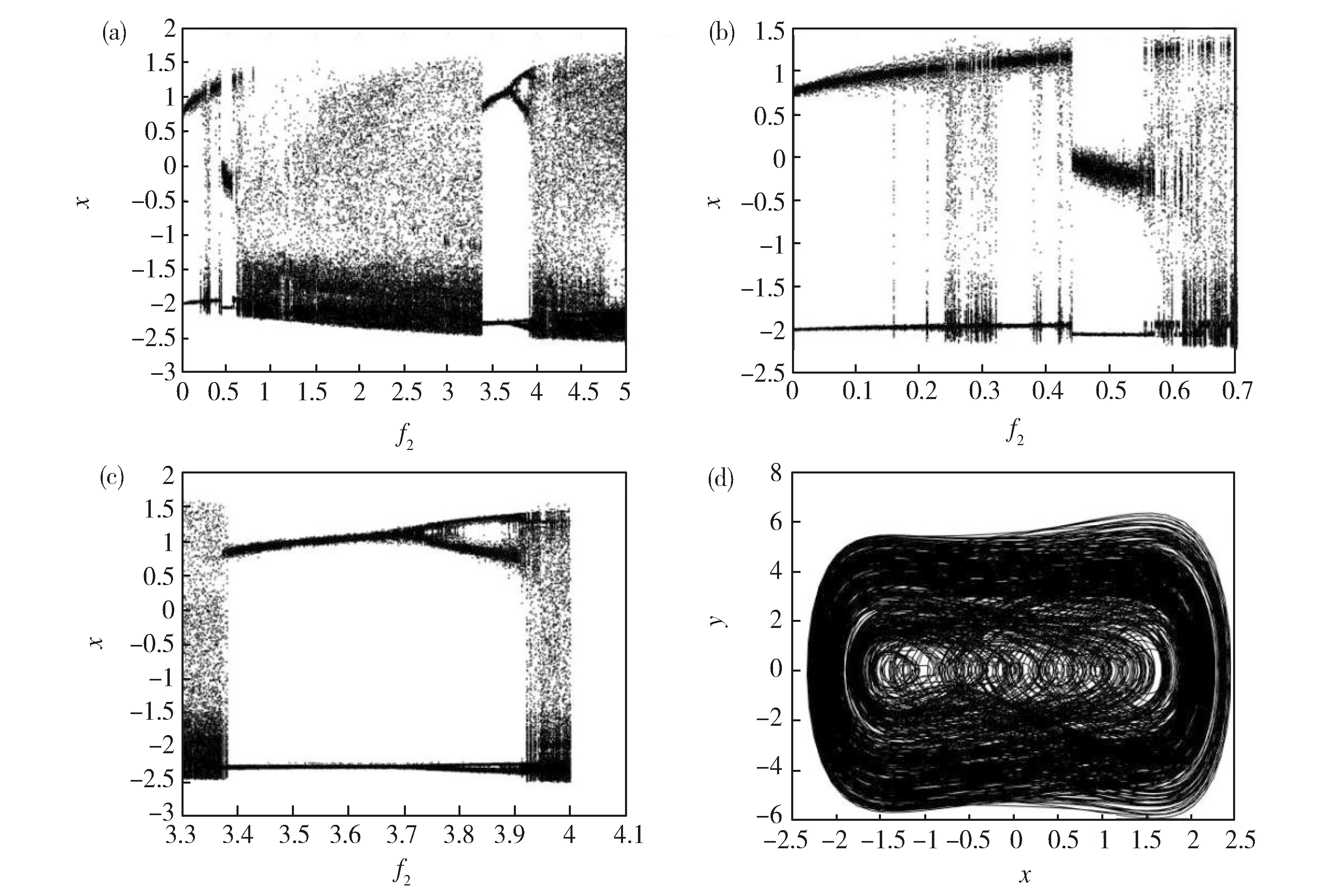
Fig.8 (a) Bifurcation diagram of the system (1) in (f2,x) plane for (b) Amplified bifurcation diagram of (a) in 0≤f2≤0.7;(c) Amplified bifurcation diagram of (a) in 3.3≤f2≤4; (d) Phase portrait of the system (1) for f2=2图8 (a)系统(1)在(f2,x)平面上的分支图,这里(b)对应于(a)在0≤f2≤0.7上的局部放大分支图;(c)对应于(a)在3.3≤f2≤4上的局部放大分支图;(d)f2=2处的相图

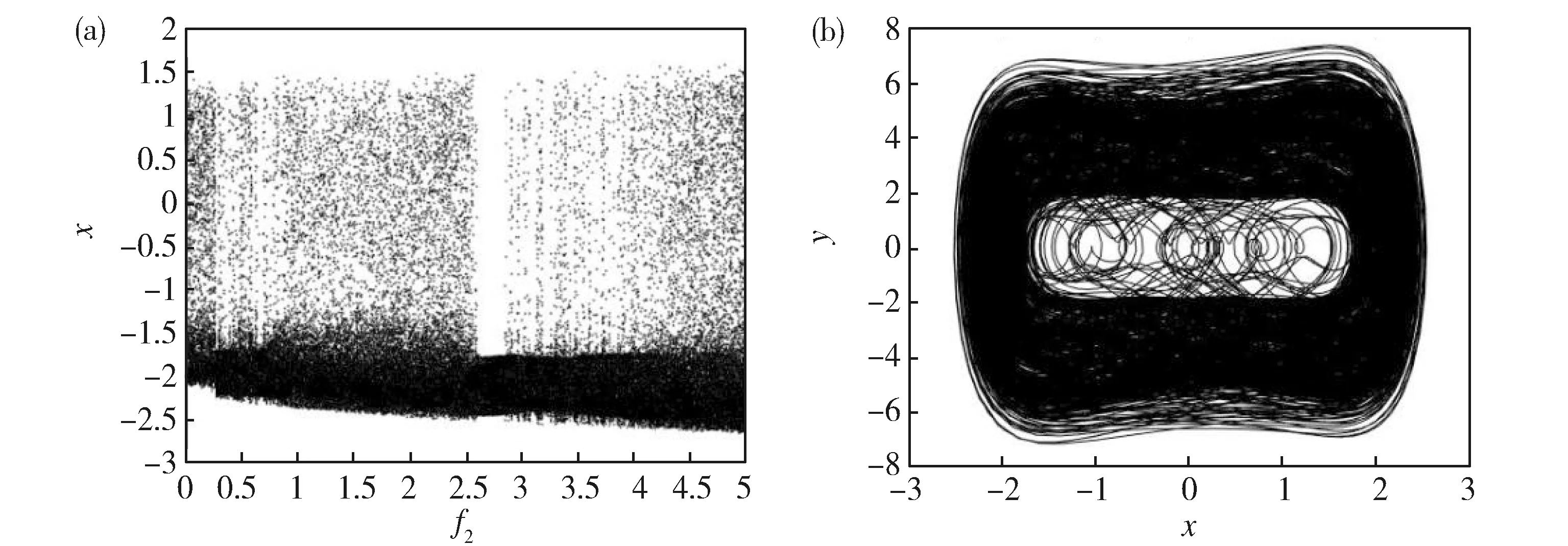
Fig.9 (a) Bifurcation diagram of the system (1) in (f2,x) plane for (b) Phase portrait of the system (1) for f2=3图9 (a)系统(1)在(f2,x)平面上的分支图，这里处的相图

Fig.10 (a) Bifurcation diagram of the system (1) in (ω1,x) plane for (b)Phase portrait of the system (1) for ω1=2图10 (a) 系统(1)在(ω1,x)平面上的分支图，这里处的相图

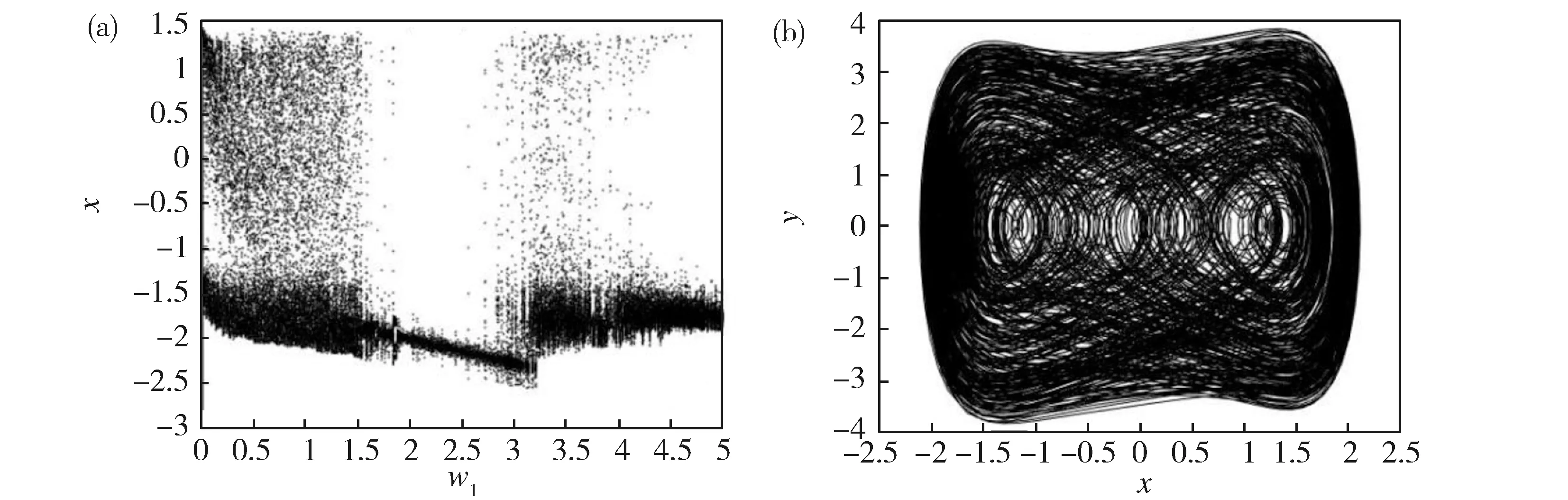
Fig.11 (a) Bifurcation diagram of the system (1) in (ω1,x) plane for (b)Phase portrait of the system (1) for ω1=1图11 (a) 系统(1)在(ω1,x)平面上的分支图，这里处的相图

4 结论

本文利用Melnikov方法研究了一类带有五次非线性恢复力和两个外力项的Duffing-Van der Pol系统的同宿、异宿分支,得到系统在周期扰动下可能产生横截同宿和异宿轨道,即产生混沌的必要条件。借助数值模拟不仅验证了理论分析结果,同时对拟周期扰动下的系统动力学进行了分析。通过研究系统随不同参数变化的分支图和相图,展现了系统具有复杂的动力学性质,包括经历倍周期进入混沌,逆倍周期进入周期轨道,带有复杂周期窗口的混沌区域,周期轨道以及拟周期轨道与混沌行为的交替转变。结论和带有三次非线性恢复力和一个周期外力项的双阱Duffing-Van der Pol系统的动力学性质相比有明显的不同。