基于改进锁相环的电动汽车用PMSM转子位置辨识方法

徐 达，杨 绿*，吴怀超，袁 焱，何 锋

(1.贵州大学机械工程学院，贵州 贵阳550025；2.贵阳航空电机有限公司，贵州贵阳550025)

永磁同步电机(Permanent Magnet Synchronous Motor，PMSM)具有高功率密度、高效率、弱磁升速能力强等特点，是电动汽车的主要动力源之一。PMSM的矢量控制需要准确的转子位置信息作为参考，编码器和旋转变压器的使用会导致电机体积增大和可靠性降低等问题，但无位置传感器技术可用于替代物理传感器的使用，为上述问题提出解决方案。在无位置传感器转子位置辨识方法中，电机反电动势因含有转子位置信息被广泛应用于转子位置辨识。滑模观测器具有结构简单、易于实现、鲁棒性强，且对被控对象参数变化不敏感等特点，被广泛应用于永磁同步电机无位置传感器控制[1]。

在传统的滑模观测器设计中，将sign函数作为滑模切换函数，因其为分段函数，会导致抖振现象。为消除传统滑模观测器的抖振效应，可重新设计滑模观测器前端的低通滤波器，文献[2]在低通滤波器的基础上引入了可调节相差的卡尔曼滤波器，文献[3]在转子位置辨识环节引入了自适应陷波滤波器来替代低通滤波器；或设计平滑的开关函数[4-5]；或应用更加准确的控制系统模型，如文献[6]建立了全阶离散滑模观测器，文献[7]则对负载转矩扰动进行估计和补偿；文献[8]根据低通滤波器的截止频率和电机电角速度设计了相位补偿方法。以上方法的控制对象均为低通滤波器的输出信号。然而，在控制系统设计中，不希望在一个控制系统中存在多个控制环节串联的设计，因为其会造成系统时间常数增大，干扰信号放大等不利影响。

在电机转子位置辨识中，利用两相反电动势构造反正切函数辨识转子位置的方法，将会放大抖振效应和电流微分相的影响，因而具有更好控制效果的锁相环被广泛用于转子位置估计。然而，文献[9]中的锁相环无法同时在电机正转和反转工况下进行转子位置辨识，且鲁棒性较差。

本文基于滑模观测器，在含有PMSM转子位置信息的反电动势辨识中，将低通滤波器的输出信号纳入滑模观测器，引入了新的锁相环用于估算正反转情况下的电机转子位置，并对改进的辨识方法进行了仿真验证。

1 滑模观测器设计

滑模观测器辨识转子位置的基本思路为，利用给定电流和反馈电流之间的误差来重构电机的反电动势，并用观测得到的两反电动势相位关系，估算转子位置和速度。将估算得到的电流值与实际电流值的误差作为输入，通过观测器控制sign函数的开关状态，其输出作为反电动势的估计值，经低通滤波器得到最终的反电动势值。在α-β两相静止坐标系下，凸极式永磁同步电机的扩展电动势的简化表达式为

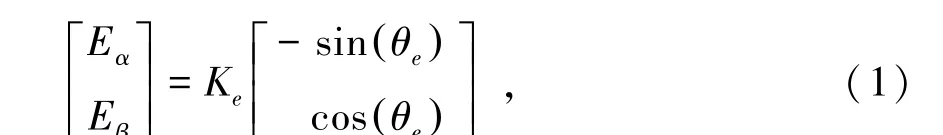
式中:系数Ke=(Ld-Lq)(ωeid-piq)+ωeψf，θe为转子电角度，p为微分算子，Ld、Lq、id、iq分别为d轴和q轴的电感和电流，ωe为电角速度，ψf为永磁体磁链。

式(1)中电机反电动势公式包含转子位置的全部信息，且与定子电流，电流微分和转子转速有关。为便于构建滑模观测器，采用PMSM电流表达式为

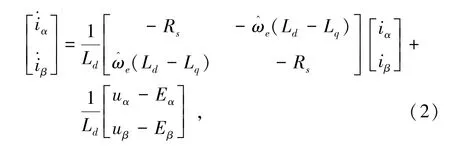
式中:Rs为定子电阻，ω＾e为电角速度估计值，uα、uβ和iα、iβ分别为 α轴、β轴的电压和电流。为获得反电动势的观测值，设计滑模观测器如下:

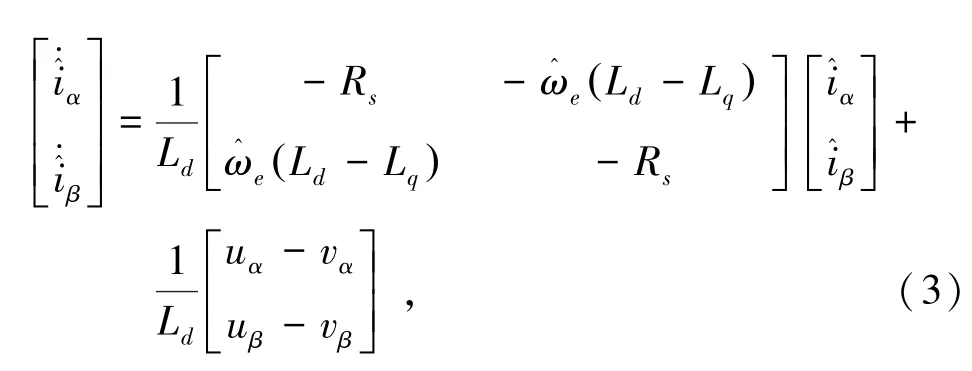
将式(4)带入式(3)并与式(2)做差，得到定子电流的误差方程为

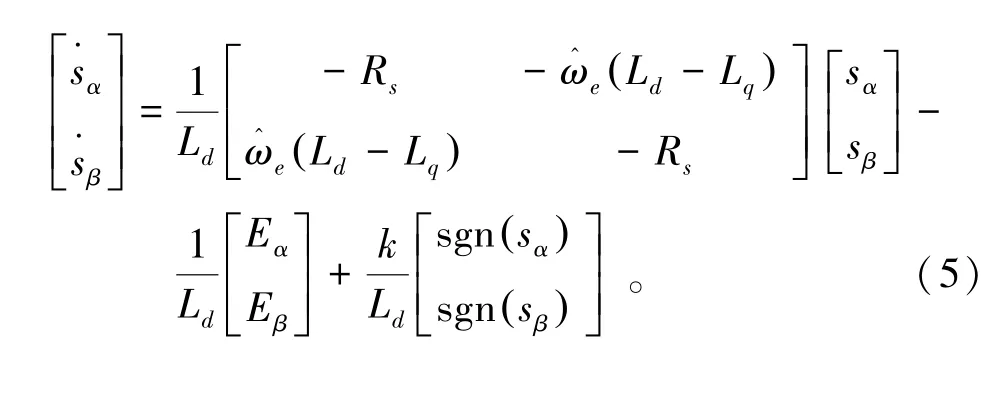
若增益k为足够大的正实数，则此滑模观测器为渐进稳定。当估计电流达到所设定的滑模区域时，其估计值将逐渐收敛于实际值附近。此时，sn=0，n=0趋近于零。为了减少其开关产生的抖振现象对控制系统的影响，需要在其前端加一低通滤波器。低通滤波器的输出信号为

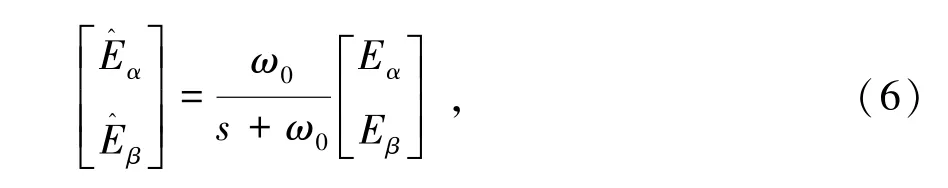
式中，ω0为低通滤波器的截止频率。在选择滤波器截止频率的时候，应选择截止频率较低且接近信号频率的，此时滤波效果最好但相位延迟却最大。本文将低通滤波器输出量α和β引入滑模观测器，滑模观测器(Sliding Mode Observer，SMO)设计如图1所示，将式(3)改写为式(7)。需注意，式(7)观测得到的电流值为式(3)中的两倍。

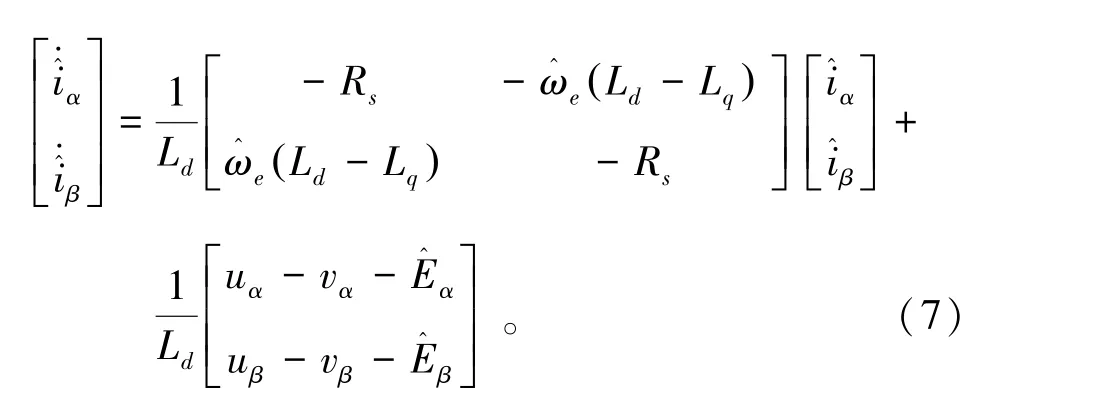
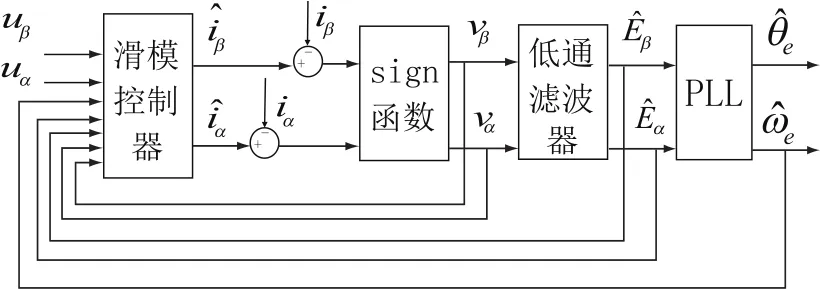
图1 改进的滑模观测器原理框图Fig.1 the diagram of modified SMO

2 锁相环设计

传统的锁相环(Phase Lock Loop，PLL)通过构造正弦函数，将式(1)中的两相反电动势引入实际转子位置和估测转子位置之差ε的表达式为

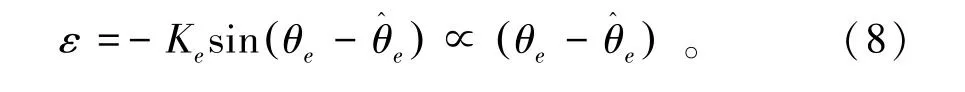
通过使用PI控制器使误差ε保持在很小的范围内，其原理框图如图2所示，图中kp和ki分别是PI控制器的比例因子和积分因子。文献[10-11]介绍了锁相环的模型归一化和参数整定方法。

锁相环的设计一般适用于正负输入的情况，在永磁同步电机的转子位置辨识得到了广泛地应用，但是其无法同时处理电机转子正向和负向转动时所产生的误差信息。这是因为传统锁相环具有多个平衡点，且每个平衡点相距π。可依据锁相环系统的敛散性将平衡点分为两类，可以收敛的是稳定点，而不能收敛的是鞍点。是否收敛取决于转速的方向，当转速反向时，锁相环系统状态始终向鞍点移动，但无法在鞍点保持收敛状态，此时转子位置辨识系统将无法保持稳定。

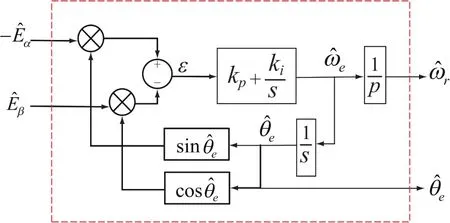
图2 传统锁相环结构框图Fig.2 the diagram of traditional PLL

传统锁相环系统的动态方程为

式中:位置误差，eθ=θe-e，转速误差eω=ωe-e。

传统锁相环系统的稳定性可以由Jacobian矩阵得到

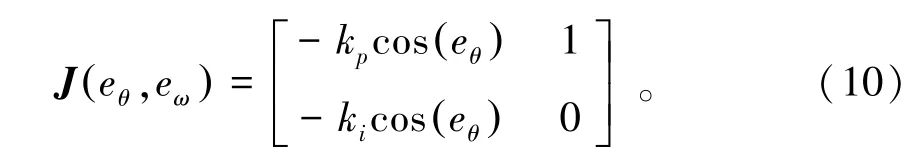
通过计算行列式的特征值，就可以获得理论平衡点。图3为传统锁相环的相位图，是电机正转，kp=1和ki=2时，转子位置误差和转速误差的轨迹图。轨迹中有两个鞍点，相位为±π；有三个稳定点，相位为±2π和0。图4为电机反转(ε→-ε)工况下的相位图，误差值符号反向使锁相环系统的稳定点产生180°的相移，造成鞍点和稳定点位置互换，其轨迹中有三个鞍点，±2π和0，两个稳定点±π。综上所述，当电机转子正转时，锁相环的稳定点相位与系统输入相匹配；当转速方向反向时，系统输入信号也发生反向，其对应的稳定点和鞍点相比原系统产生了180°的相移，鞍点和稳定点位置互换，使转子位置辨识误差无法收敛，造成系统无法保持稳定，最终导致了控制系统鲁棒性差的结果。为了解决传统锁相环转子位置辨识系统只可以单方向辨识转子位置的问题，可设计转速方向跟随的锁相环，以动态调整PI观测器的kp和ki值。

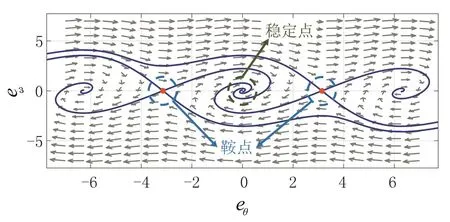
图3 正转时传统锁相环的相位图Fig.3 the phase graph of traditional PLL when positively rotating

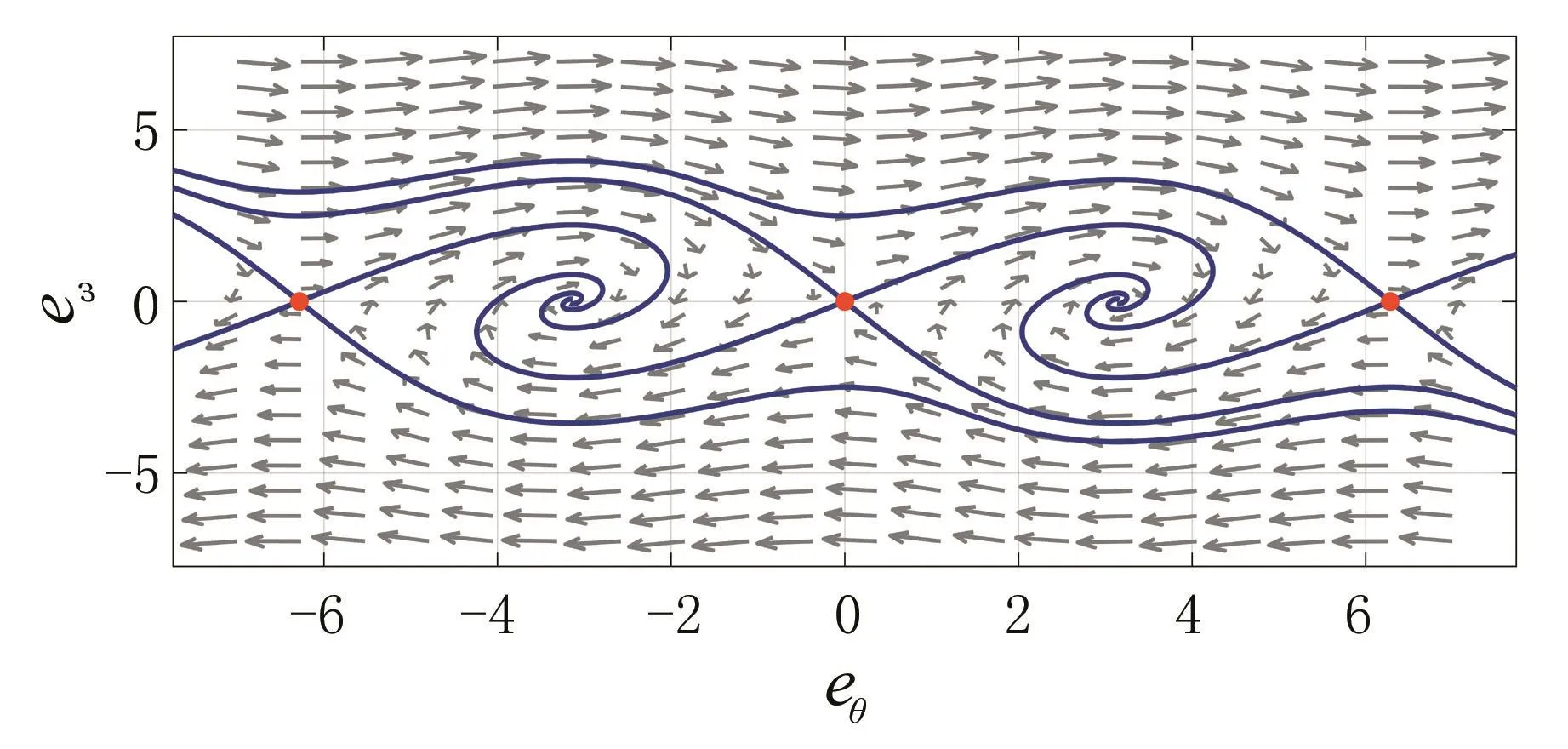
图4 反转时传统锁相环的相位图Fig.4 the phase graph of traditional PLL when negatively rotating

为了改进原锁相环方法无法适应换向工况的缺陷，参照文献[12]，设计新锁相环理论框图如图5。为了不引入增益Ke的误差，在第一步使用除法；并在第二步构造含有转子位置信息的正切函数。其表达式为

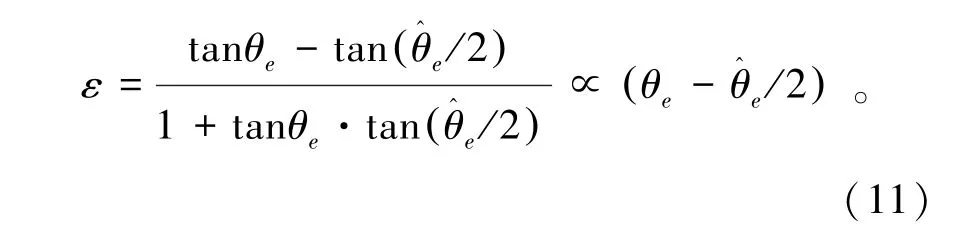
此改进锁相环与传统锁相环相比，在误差函数中消除了增益Ke的影响，而且具有较大范围的灵敏度；当速度反向时，多增加一个自由度，不会导致误差参数的符号改变，所以PI控制器参数不经整定也可适用于电机正转和反转工况。

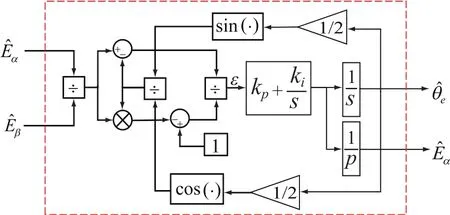
图5 改进锁相环的结构框图Fig.5 the diagram of proposed PLL

改进锁相环平衡点的位置与正切函数相关，正切函数在单周期内为单调函数，周期为π。画出相位图轨迹如图6，没有鞍点和稳定点的变化，而只具有稳定点。无论转速方向，系统中的转子位置和速度误差都向零位运动，整个转子位置辨识系统进入锁相状态。

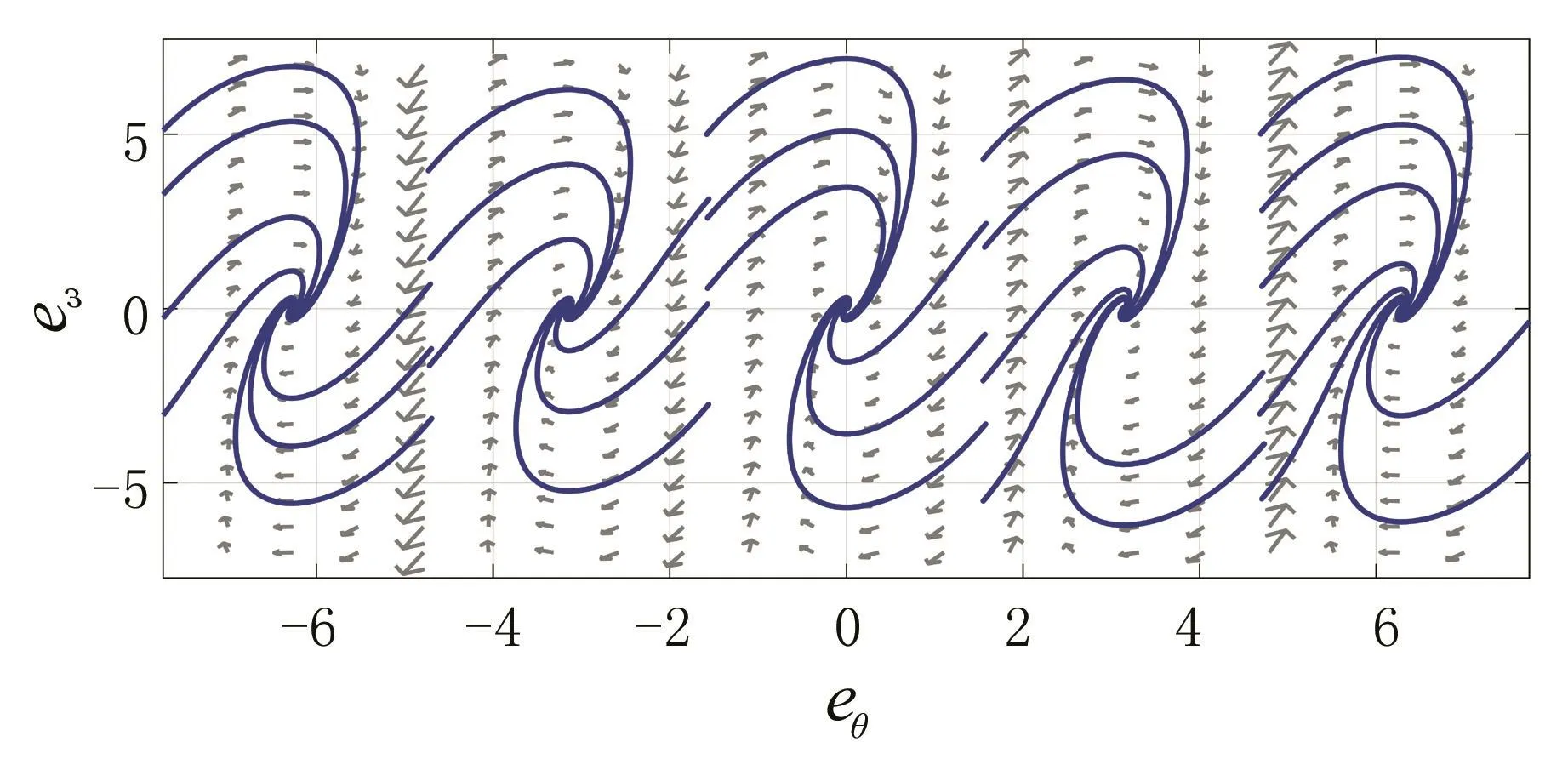
图6 改进锁相环的相位图Fig.6 the phase graph of proposed PLL

3 仿真验证

基于MATLAB/Simulink仿真平台搭建了电动车用PMSM无位置传感器转子位置辨识模型。电机参数如表1[13]。

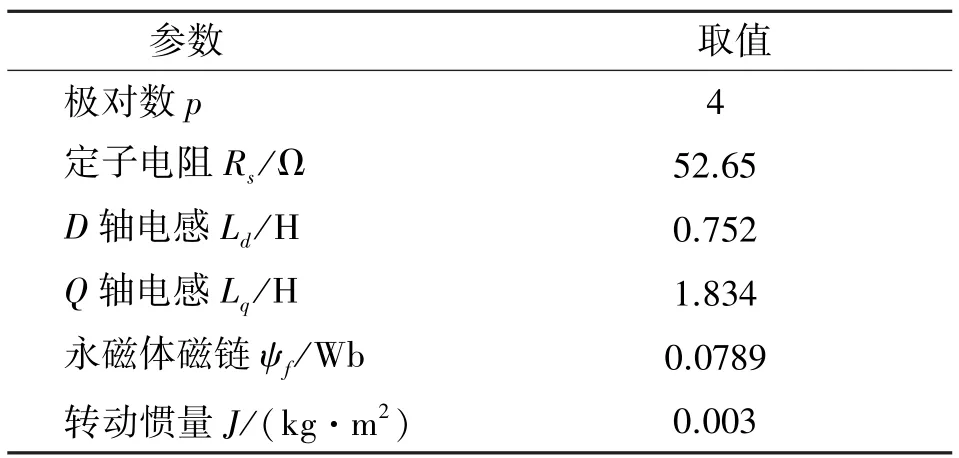
表1 电机参数表Tab.1 the motor parameter table

为了验证转子位置辨识方法的动态跟踪性能，给定电机转速斜坡信号输入，并在0.2～0.4 s施加5 N·m的脉冲转矩，以模拟负载突变的工况。实际转子位置和辨识转子位置如图7，转子位置辨识误差如图8。在起步阶段转子位置辨识出现较大幅度震荡，但位置误差能够快速收敛于0.15 rad附近。0.2 s时，位置辨识误差突增0.05 rad，但又快速减小，在0.4 s负载撤去后，转子位置辨识精度提高。

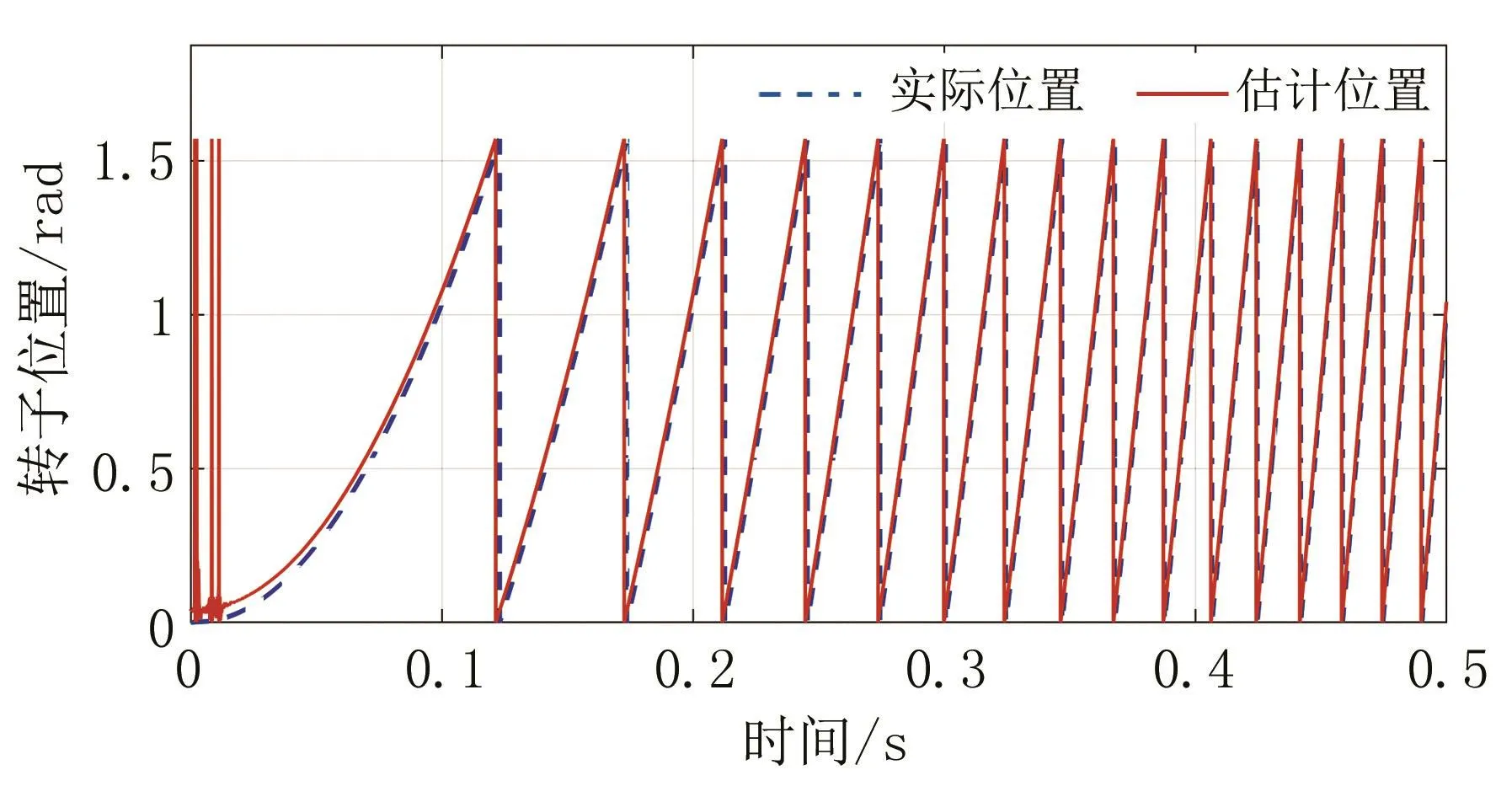
图7 速度斜坡信号输入的转子位置对比图Fig.7 the position comparison with ramp speed signal

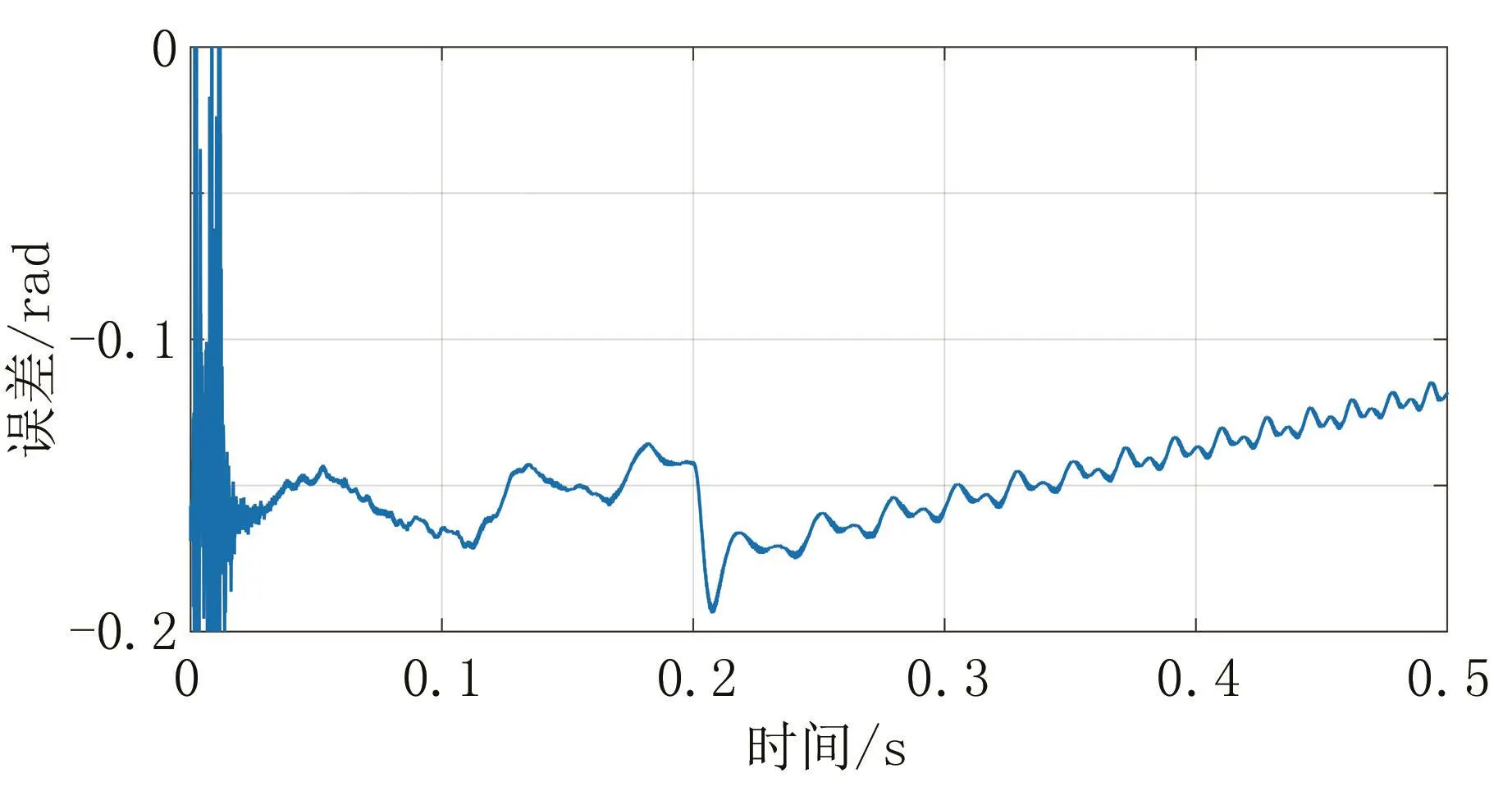
图8 速度斜破信号输入的转子位置误差图Fig.8 the position error with ramp speed signal

为了验证改进转子位置辨识方法的速度反向辨识功能的有效性，在电机启动时给定1000 r/min的转速阶跃信号，在0.2～0.4 s时，电机匀减速至-1000 r/min后保持匀速。同时，在0.2～0.4 s施加15 N·m的脉冲转矩。实际转子位置和辨识转子位置如图9，转子位置辨识误差如图10。在速度反向的过程中，在速度跨越零点时产生了震荡，但很快收敛，估计转子位置能够较好地跟踪实际转子位置。

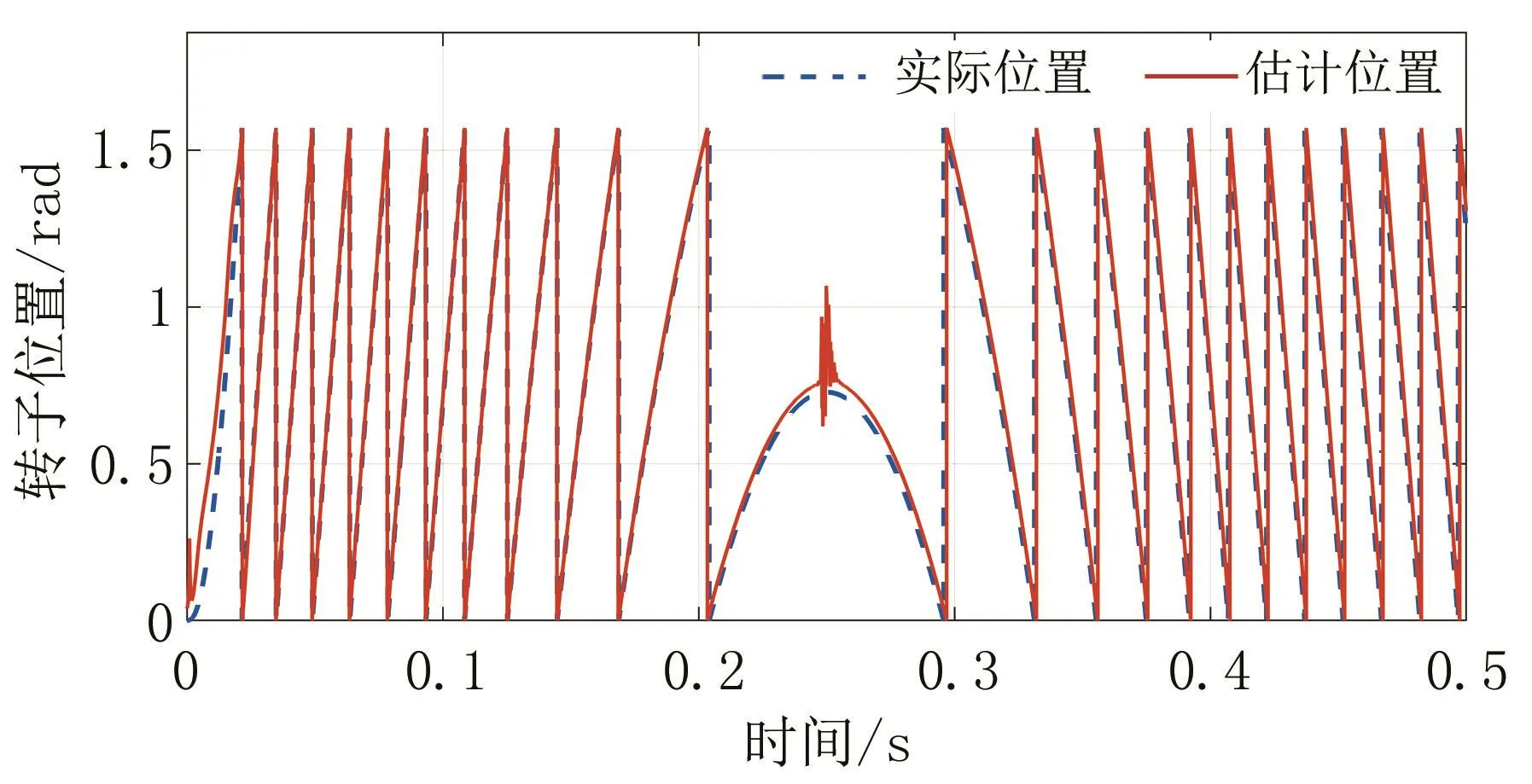
图9 速度反向的转子位置对比Fig.9 the position comparison with reversed speed signal

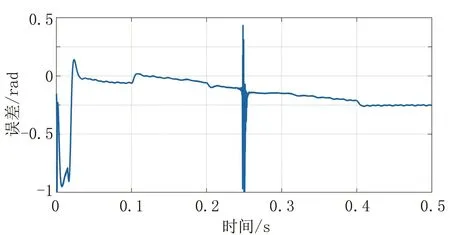
图10 速度反向的转子误差Fig.10 the position error with reversed speed signal

4 结语

本文将低通滤波器的输出纳入滑模观测器中，缓解了相位滞后的问题，并从系统稳定点设计的角度证明了此系统的鲁棒性。仿真结果表明，基于改进锁相环的永磁同步电机无位置传感器转子位置辨识方法具有良好的动态特性和鲁棒性，且改进的锁相环可以进行无方向差别的转子位置辨识，该方法在建立模型时无需考虑参数归一化的问题，而且避免了传统锁相环在速度反向时，需调节PI观测器参数的问题，降低了转子位置辨识系统的复杂度和设计难度。