一类分数阶阻尼系统的可控性

秦海勇，梁家辉，路 奕

(1.齐鲁师范学院 数学学院，山东济南250200；2.山东大学 控制科学与工程学院，山东 济南250061)

最近几年，分数阶微积分在软物质、光学、工程学、流变学、量子力学、信号处理、反常扩散和图像处理等领域得到广泛应用，国内外学者取得一系列的重要结果。文献[1]研究了分数阶微积分在汽车空气悬架半主动控制中的应用，有效地抑制车身共振，提高乘坐舒适性。文献[2]研究分数阶在基于滑模控制技术的永磁同步电机控制中的应用，有效地消减传统永磁同步电机滑模控制系统中的震动，还保持了系统对参数和外部扰动的强鲁棒性，使得系统达到了较高的综合控制性能。文献[3-7]研究了分数阶微积分在胶凝原油、人工冻土遗传、沥青胶砂、图像去噪和固体材料方面的应用。文献[8-11]基于分数阶微积分理论，研究了宽带噪声、1/4悬架模型时滞反馈控制和经济波动模型稳定性等方面问题，这些应用研究都取得有效成果。利用分数阶微分方程建立的控制系统模型比整数阶控制系统模型，更能准确描述相关系统的特性，这主要表现在分数阶微积分对事物的描述具有记忆性，而整数阶没有这样的性质。因此，研究分数阶微分方程理论在控制系统中的应用具有重要的理论和应用价值。

本文研究如下线性分数阶阻尼动力系统

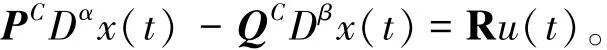
同时，考虑如下非线性分数阶阻尼系统PCDαx(t)-QCDβx(t)=R u(t)+G f(t，x(t)，x′(t))。其中1＜ α ≤2，0＜ β≤1，u∈L2(J，Rm)，x∈Rn，P，Q，G是n×n矩阵，R是n×m矩阵，并且f∶J×Rn×Rn→Rn是一个连续函数。

采用逐次逼近的迭代方法来证明非线性分数阶阻尼系统的可控性。

1 预备知识以及引理

定义1[12]米塔格-累夫勒(Mittag-Leffer)函数定义为

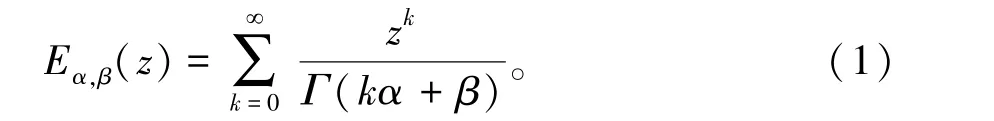
其中α ＞0，β＞0，z∈C。特别地，当β=1时，简记为

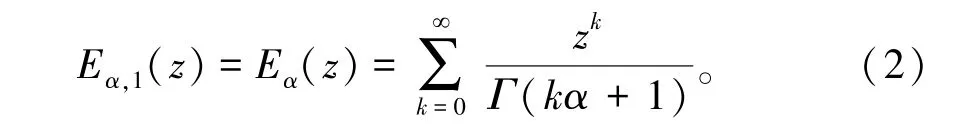
性质1[12]

其中

特别地，当k=0时，

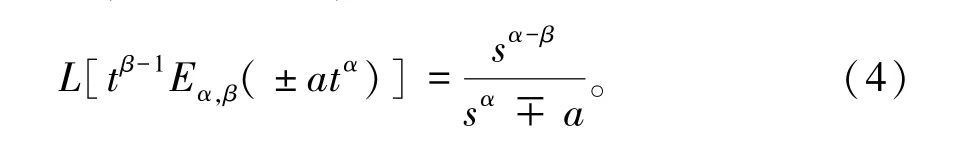
定义2[13-14]米塔格-累夫勒矩阵函数为

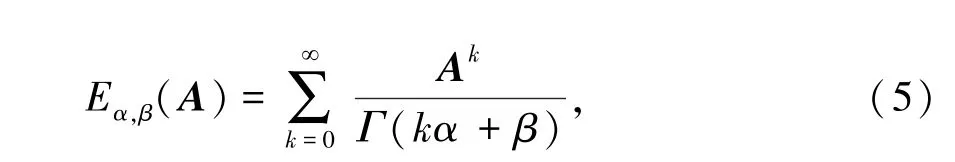
其中，A是n×n矩阵。

性质2[14-15]

特别地，当k=0时，

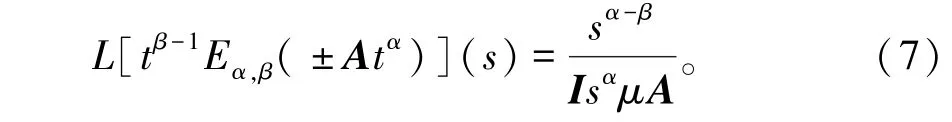
这里的α、β大于0，I是单位矩阵。

定义3[16]卡普托(Caputo)分数阶导数

当a=0时，简单记C0Dα为CDα，由定义可得Caputo分数阶导数的拉普拉斯变换[12]为

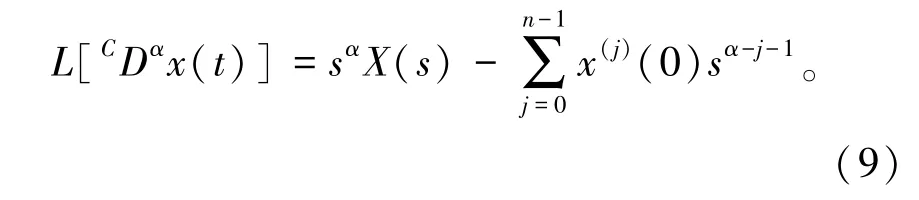
当0＜α≤1时，

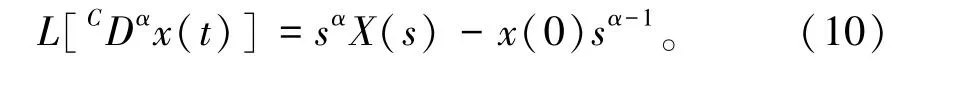
当1＜α≤2时，

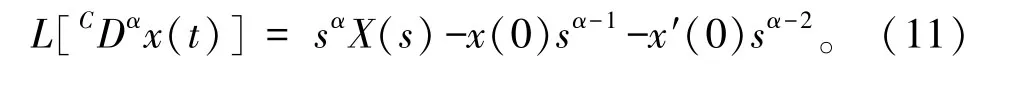
定义4[14]对于柯西问题

其中t∈[0，T]∶=J，1＜ α≤2，0＜ β≤1，A是n×n矩阵，这个方程的初值解如下:

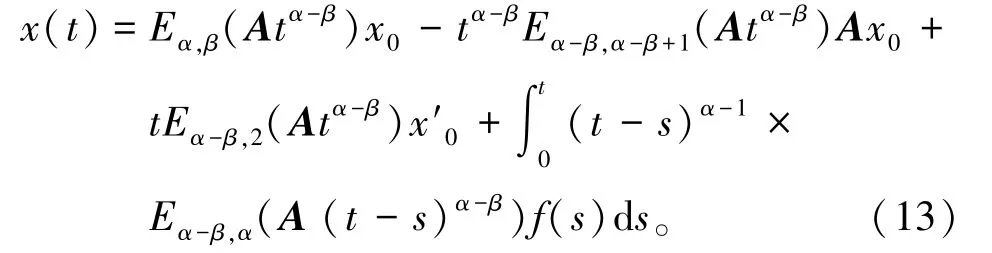
如果对于每一个向量x0，x′0，x1∈Rn，都存在一个控制f(t)∈L2(J，Rm)，使得方程有解为(13)，且x(0)=x0，并且满足x(T)=x1，那么称(12)在J上是可控的。

引理1[14]设分数阶线性系统由下列分数阶微分方程表示

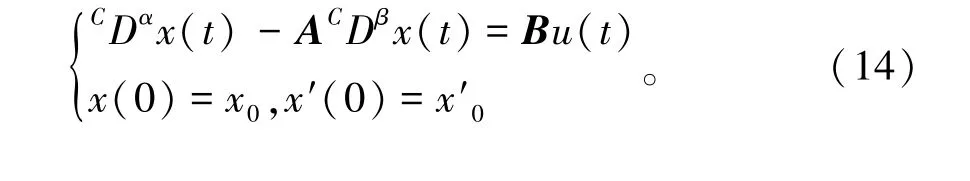
其中t∈[0，T]∶=J，1＜ α≤2，0＜ β≤1，x∈Rn，u∈L2(J，Rm)，A、B分别是n×n和n×m矩阵。当且仅当格兰姆矩阵

可逆时，(14)是可控的。并且相应的解可以写成

这里

2 主要结果

定理1设P，Q是n×n矩阵，R是n×m矩阵，线性动力系统由下列分数阶微分方程表示

其中t∈[0，T]∶=J，1＜ α≤2，0＜ β≤1，x∈Rn，u(t)∈L2(J，Rm)。

当满足下列条件(i)，(ii)时，系统(16)是可控的。

(i)矩阵P可逆。

(ii)当且仅当格兰姆矩阵

可逆。其中，控制函数

这里，

证明:对(16)式方程两边同时进行拉普拉斯变换得

移项并两边同时左乘逆矩阵(P sα-Q sβ)-1，得

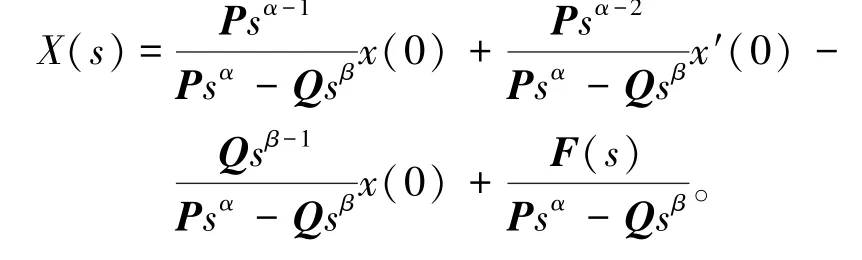
由于矩阵P可逆，所以

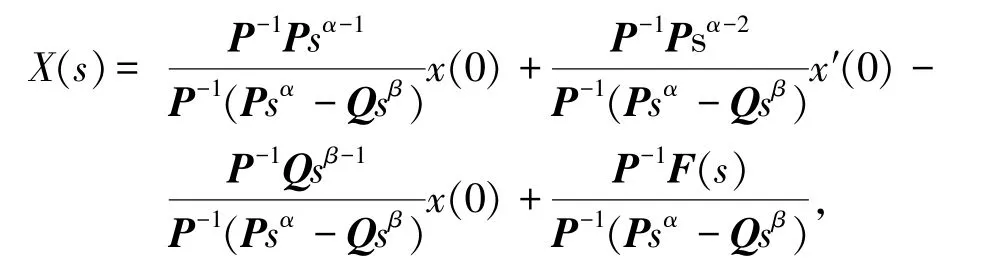
即

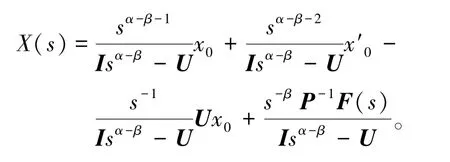
其中I为单位矩阵，F(s)=L[R u(t)]，矩阵U=P-1Q。再对上式进行拉普拉斯逆变换得

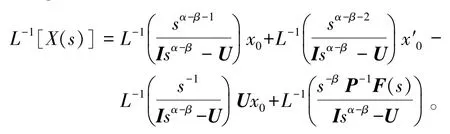
再用拉普拉斯逆变可得方程的解为

因此，由引理1知，(16)式在J上是可控的。

注1：从定理1可以看出，引理1是定理1特殊情况。在矩阵P=I的情况下，即可得到引理1的结果。

下面考虑如下非线性分数阶动力系统

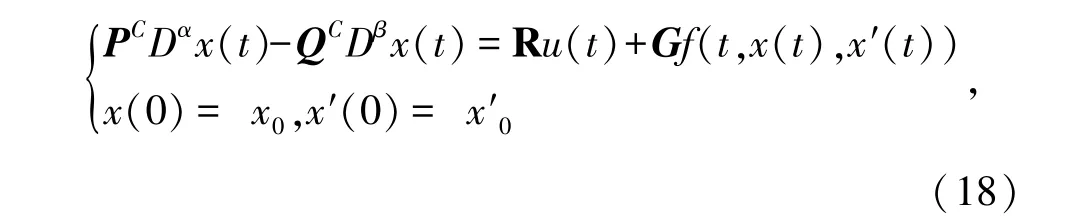
其中t∈J，x∈Rn，u∈L2(J，Rm)，0＜β≤1，1＜α≤2，P，Q，G是n×n矩阵，R是n×m矩阵，其中P是可逆矩阵，并且f∶J×Rn×Rn→Rn是一个连续函数。

我们定义

为巴拿赫空间，其范数是

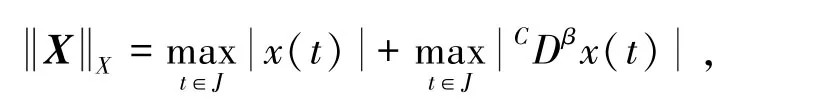
其中0＜β≤1。为了方便，记U=P-1Q，V=P-1R，C=P-1G。

并假设以下式子成立:

定理2设(18)式中函数f满足条件(I)和(II)，若分数阶线性系统(16)在J上是可控的，则非线性分数阶系统(18)在J上也是可控的。

(I)存在连续函数w(t)使得

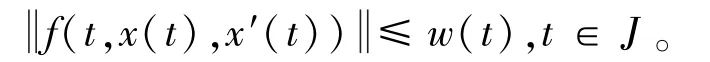
(II)存在连续二元函数 μ(s，t)，v(s，t)始终大于零，使得

其中 μ(s，t)∶J×J→R，v(s，t)∶J×J→R。

证明：由于P是可逆矩阵，所以(18)式可以转化为等价方程

要证明(18)可控，只需证明(19)式可控即可。下面证明(19)式是可控的。

设函数列为{xn(t)}，并定义

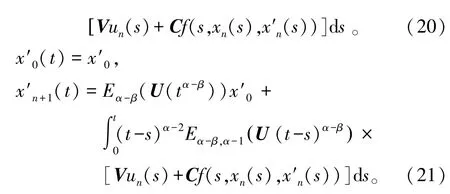
其中

显然有

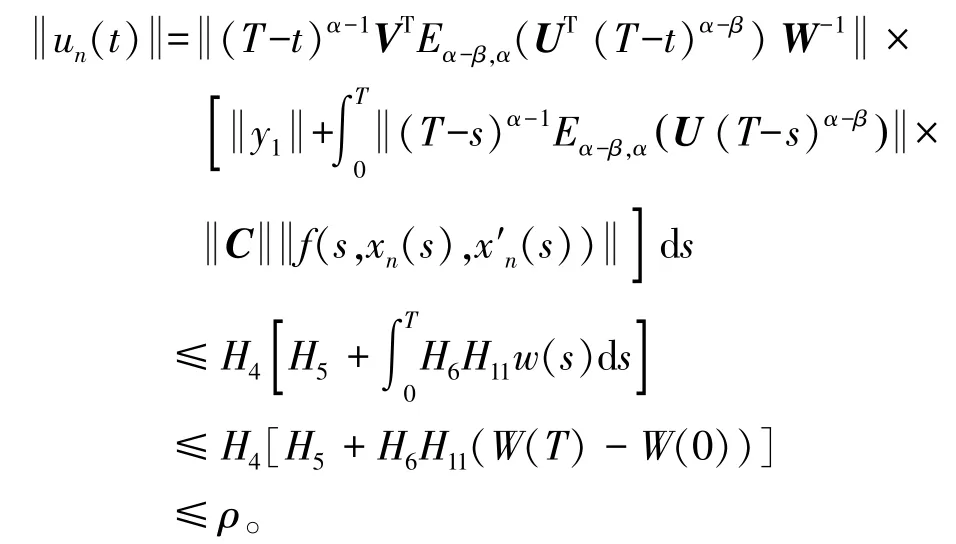
其中W(t)是w(t)的一个原函数，并且

因此有

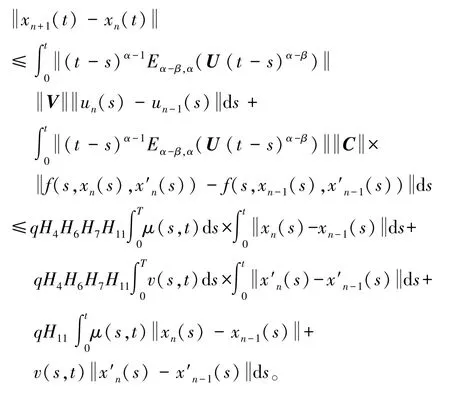
由于μ(s，t)，v(s，t)在有界闭矩形J×J上，所以分别存在正数N＞0，M＞0使得μ(s，t)≤N，v(s，t)≤M。所以

进一步有

由于W(t)是在[0，T]上连续，所以有界。因此存在R0＞0，θ＞0使得

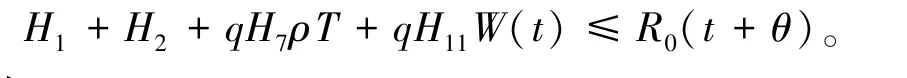
另外

由于W(t)是在[0，T]上连续，所以有界。因此存在L0＞0，δ＞0使得

假设T≥0，并用数学归纳法可得到下边不等式

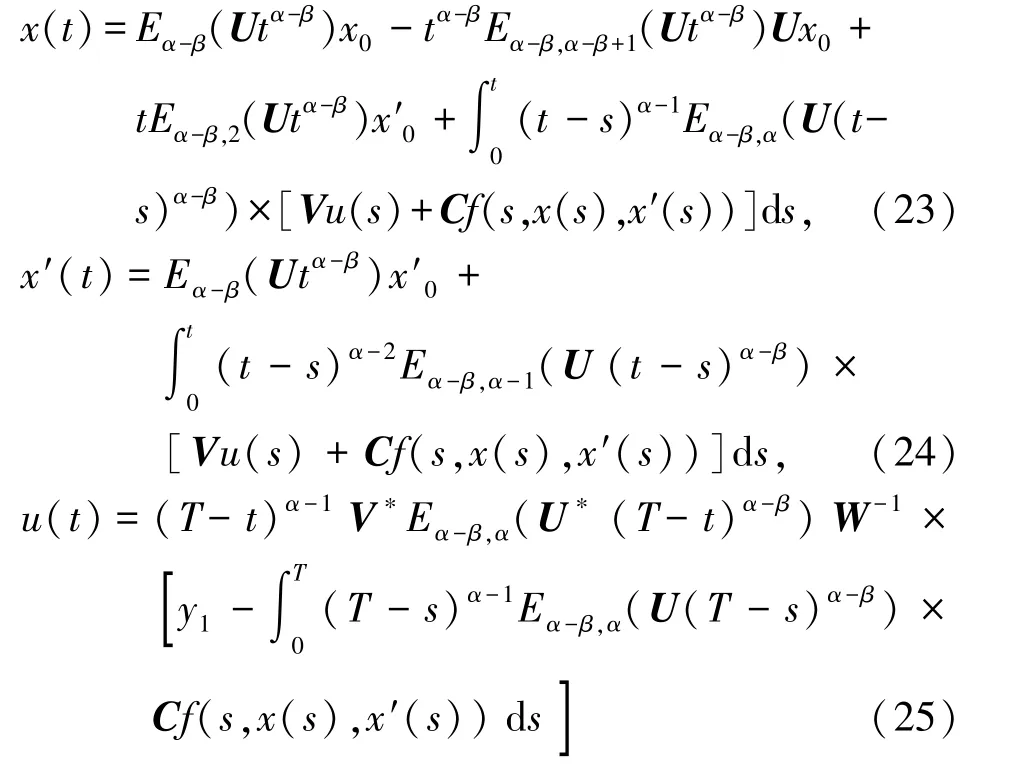
分别看成是(20)、(21)、(22)式左右两边同时取极限而得到的。

并且有

很显然当n→∞时有CDβxn+1(t)→CDβx(t)。这说明函数列xn(t)的极限是方程的解。

又因为

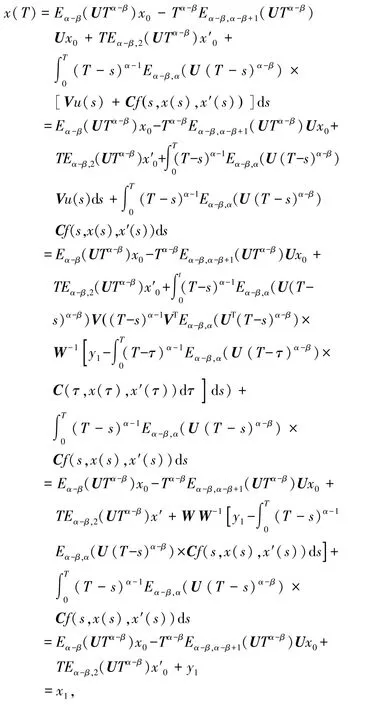
根据可控性的定义知，系统(19)在J上是可控的，所以(18)式在上J可控。证毕。

3 数值例子

考虑下列非线性分式系统

其中，t∈[0，2]，初始条件为x0将方程(26)与(18)比较可知，P=

所以格兰姆矩阵W可逆，相应的分数阶线性系统在[0，2]上是可控的。显然，系统中的非线性项f(t，x(t)，x′(t))在[0，2]上是连续的有界函数，满足条件(II)。 可取 μ(s，t)=v(s，t)=2，定理2的条件(I)、(II)都满足，因此分数阶非线性系统(26)在[0，2]上是可控的。这时可以得到该系统的状态轨迹(图1)和控制函数(图2)。

图1 状态轨迹Fig.1 Trajectory of states

图2 控制轨迹Fig.2 Trajectory of control

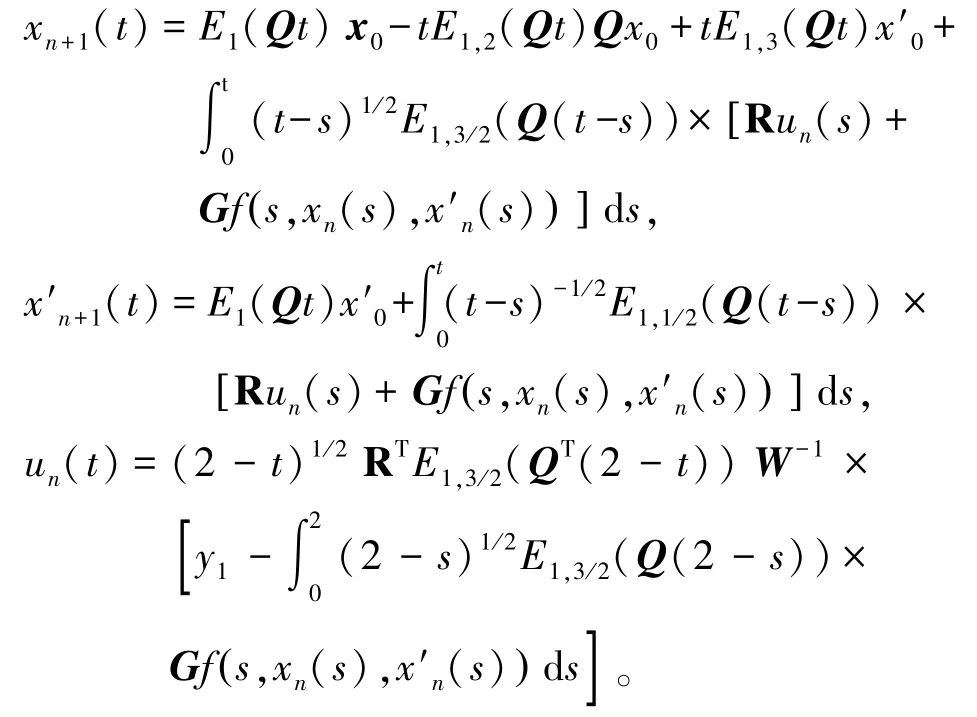
其中n=0，1，…，使用Matlab仿真，即得到图1和图2。

4 结论

在本文中，通过逐次逼近的方法证明了非线性阻尼系统的可控性，并利用数值解的方法仿真了实例，证实了结论的有效性和可行性。