基于活动网络的体系能力依赖关系分析方法*

郑 剑,刘俊先,陈 涛,李清韦

(国防科技大学信息系统工程重点实验室,湖南长沙 410073)

随着信息化水平的提高,军事体系的网络化特点也越来越突出,关系越来越复杂。体系的建设和管理对体系的评估产生强烈的需求,而能力评估是体系评估的重点。当体系有多项能力时,如何分析它们之间的相互关系,如影响、依赖、包含等,对开展后续评估工作十分重要。

国内外对系统的研究已较完备,但对体系的研究还处在新兴阶段。John H. Gauthier等用一组适应性指标来量化动态体系的效率和有效性,并评估适应性指标在对体系的适应性性能量化方面的有用性[1]。赵青松等在针对体系的目的、能力和任务要求等关系分析和研究的基础上,提出了体系任务-能力概念格这一思想,并且探讨分析了针对任务目标的体系能力相关问题,还提出了体系能力关联的抽取算法以及体系能力关联集的相关计算方法[2]。但上述方法未能较好地分析体系能力之间的关系问题。

本文针对体系能力评估中依赖关系,研究体系、能力、活动的概念及内涵,提出基于活动体系能力建模方法,建立活动网络,构建环路查找算法，找出其中所有环路,提出基于活动环路的能力依赖关系分析方法

1 体系能力概念与建模

1.1 能力的相关概念与模型

能力是为了达到一定的目标,在规定的要求和前提下,采用不同方式方法执行一组活动的本领。活动形成能力,体系能力的实现是通过活动效果来体现的,所以能力评估的对象应该是活动效果。活动是由执行者完成,执行时消耗和产生资源。所以应该以活动为起点对能力进行评估,经过活动的效果,找出能力和效果之间的对应关系,利用对活动效果的评估来对能力进行评估。条件由当前法规标准所决定影响。执行者不单单指人才力量,还和信息系统以及装备设施相关联。并且通过相应训练,可以提升活动和能力。

基于上述分析,本文建立了体系能力的概念模型,如图1所示。

图1 体系能力的概念模型

体系的目标是要完成一定的使命及任务,因此针对每一任务要有完成该任务的能力,这样根据可能的任务,可以确定体系最高能力。每项任务可以分解为一系列活动[3],对每项活动都要遵循一定的准则或约束,在一定的资源(人才、技术、设施等)的支撑下,产生预先计划的输出,因此每项活动对应着一项体系能力。对活动进行进一步分解分析,可以得到支撑活动完成需求的下一层活动,每一项活动对应着一项体系的能力。分解活动直至一定的粒度,则可以得到对应的层次体系能力。

1.2 能力建模方法

能力建模方法

基于以上分析，可以按照如下步骤来对体系能力进行建模：

1)分析体系使命任务，记所有使命任务为{missioni}，其中missioni表示第i项使命任务，对每一任务生成一项体系顶层能力，记顶层能力集合为{capi}，其中capi表示第i项能力。

2)对任务missioni进行分析，建立其活动模型，设所有活动集合为{acti}，其中acti表示第i项活动，则对顶层能力capi，建立其子能力capj，其中acti与capj相对应。

3)根据活动的分解关系，逐层建立分能力或子能力指标。

由活动分解关系矩阵CAA可知，某活动分解对应子活动可用CAA的相应行向量表示，CAA的元素为0/1， 0/1表示活动acti是否可分解得到活动actj，若可分解得到，则值为1，反之则为0。若某活动相应行向量元素全为0，可知该活动为最底层节点活动，不可再分解。

能力分解关系矩阵为CCC定义与活动分解关系矩阵CAA类似，某能力分解对应子能力可用CCC的相应行向量表示，CCC的元素为0/1， 0/1表示能力capi是否可分解得到能力capj，若可分解得到，则值为1，反之则为0。若某能力相应行向量元素全为0，可知该能力为最底层分能力，不可再分解。

为了分析能力的影响依赖关系，在分析活动时，要刻画活动之间的各种关系(信息关系、资源流关系等)。记所有活动间的关系矩阵为CAR，CAR的元素为0/1， 0/1表示活动acti是否有信息/资源输出到活动actj。

记所有活动集合为SA={acti}，所有能力集合为SC={capi}，活动分解关系矩阵为CAA，能力分解关系矩阵为CCC，活动与能力映射关系矩阵为CAC，活动间的关系矩阵为CAR，则体系能力可以用六元组建模，即

SoS-cap=SA，SC，CAA，CCC，CAC，CAR

(1)

设某陆军武器装备体系中含有一项使命任务，即陆军部队执行攻打敌阵地任务，记该使命任务为mission1，对该任务生成一项体系顶层能力即突破占领敌阵地能力，记该顶层能力为cap1。对使命任务为mission1进行分析，设所有顶层作战活动集合为{acti}，则对能力cap1，建立其子能力capj，其中actj与capj相对应，根据作战/信息活动的分解关系，逐层建立分能力或子能力指标。同时建立其活动模型，如图2所示。其中，快速占领能力与指挥控制、综合保障等活动相对应，火力突击能力与战场感知、火力打击等活动相关。

其中该使命任务最终可分解为13个活动，记所有活动集合为SA={acti，1≤i≤13}，其中，act1：陆军攻打阵地，act2：快速占领，act3：后勤保障，act4：特种突袭，act5：火力突击，act6：立体攻防，act7：信息保障，act8：指挥控制，act9：战场感知，act10：综合保障，act11：防空反导，act12：火力打击，act13：兵力突击。所有的能力集合为SC={capi，1≤i≤7}，其中cap1：陆军攻打阵地能力，cap2：快速占领能力，cap3：后勤保障能力，cap4：特种突袭能力，cap5：火力突击能力，cap6：立体攻防能力，cap7：信息保障能力。活动与能力映射关系矩阵为CAC活动分解关系矩阵为CAA，能力分解关系矩阵为CCC，分别如表1、表2和表3所示。图中箭头表示为该活动相对应能力。

活动与能力映射关系矩阵为CAC，如表1所示。

活动分解关系矩阵为CAA如表2所示。

能力分解关系矩阵为CCC如表3所示。

2 体系的活动网络环路查找方法

活动产生能力，体系能力的实现是通过活动效果来体现的，所以能力评估的对象应该是活动效果，对能力的识别分析是在活动的基础上进行的。而对体系能力进行分解，可得到最底层的活动。由活动分解关系矩阵CAA可知，若某活动相应行向量元素全为0，可知该活动为最底层节点活动，不可再分解。记所有最底层活动集合为

(2)

图2 陆军武器装备体系任务与能力关系图

表1 陆军武器装备体系作战能力对活动映射矩阵

表2 陆军武器装备体系活动分解关系矩阵

表3 陆军武器装备体系能力分解关系矩阵

(3)

cij=1表示活动acti有到actj的信息，否则为0。基于活动网络遍历可能存在的活动回路，即所有闭合的没有重复节点和边的路。

其中，n×n矩阵M称为图D的可达性矩阵。

环路分析通常是找出给定的活动网络中存在的回路，对这些回路进行分析探讨。信息交流通常是形成一个完整的回路，即在环路中进行传递。根据OODA环理论，指挥控制作战的特点是按照观察—判断—决策—行动( OODA) 环路进行的战斗[4-5]，作战网络中必然存在很多环。而本文中的活动网络是根据体系任务分解得到的，通常一个任务完成是需要信息在活动中交流传递构成一个回路，这样根据环路分析显得更有意义。

本文采用邻接表方法来贮存有向图，利用深度优先遍历算法，使得给定一个活动网络有向图后，能够快速找出该图中含有的全部回路[6]。

3 基于活动环路的能力依赖关系分析方法

3.1 基于活动环路的能力依赖关系分析

对体系能力进行分解，可得到最底层的活动。记给定活动网络D中的环路为σi，其中共有n个环路，则所有环路集合记为S环={σi，1≤i≤n}。

由上所述，由最底层的活动可以得到所对应底层所有能力之间的依赖关系。而能力分解关系矩阵CCC中相应行向量可表示高层次能力分解对应子能力。所以根据最底层能力之间的依赖关系，同样可以得出所有能力之间的依赖关系。

首先对体系能力进行建模，建立其活动模型，并且进行逐层分解，并建立其对应分能力，直至分解到最底层活动。然后从底层活动出发，基于其交互关系分析得到活动网络图，分析其中所有环路关系，找出回路中的活动所对应的能力之间的依赖关系，进而得到底层所有能力之间的依赖关系，利用能力分解关系矩阵CCC，进而可以得出所有不同层次能力之间的依赖关系。流程如图3所示。

图3 体系能力依赖关系分析流程图

所有层次能力之间的依赖关系即活动网络体系能力之间的依赖关系可以用一个矩阵CD来表示，CD中的元素为

3.2 能力依赖关系级别划分

活动网络体系能力依赖关系可用一个CD来表示。则可对这个矩阵进行级别划分来明确各能力之间的层次关系。

首先通过可达性矩阵，给出可达集以及先行集的定义。

如体系能力SC={capi，1≤i≤n}，可达性矩阵为CD=(dij)，则∀capi∈SC的可达集为

R(capi)={capj|capj∈SC，dij=1}

(4)

capi的先行集为

A(capi)={capj|capj∈SC，dji=1}

(5)

这两个集合在可达性矩阵中是很直观的。这个矩阵里，沿着capi行横着看，所有元素为1的列相对的能力都应该属于R(capi)；沿着capi列竖着看，所有元素为1的相对的能力都应该属于A(capi)。

如某能力capi为顶级能力，由于capi不能到达更高级能力，因此该能力的可达集R(capi)中只有capi本身以及和它同一级的强连接能力；且先行集A(capi)只有它自己以及能够达到它的下一级能力和与它同一级别的强连接能力。这样一来，就顶级能力capi来看，先行集A(capi)与可达集A(capi)的交集与R(capi)一样，因此提出能力capi为顶级能力的条件为

R(capi)=R(capi)∩A(capi)

(6)

即可给出最上级能力集的定义如下：

体系能力SC={capi，1≤i≤n}的最上级能力集为

T=capi|capi∈SC且R(capi)=R(capi)∩A(capi)

获得顶级能力之后，将这些顶级能力先除去，同理即可获得下一级别的能力。一步步进行下去，能把各能力划分成一级级。如果用L1，L2，…，LK表示从上到下的各级，则体系能力SC的级别划分可用式(7)表示

π(SC)={L1，L2，…，LK}

(7)

具体按以下步骤反复进行。

1)Lj={capi∈SC-L0-L1-…-Lj-1|Rj-1(capi)∩Aj-1(capi)=Rj-1(capi)}

这里，L0=∅，Lj表示第j级，j≥1

Rj-1(capi)={capi∈SC-L0-L1-…-Lj-1|mij=1}

2)SC-L0-L1-…-Li=∅时，级别划分完毕；反之，若SC-L0-L1-…-Li≠∅Ø，则令j=j+1，返回步骤1)。

根据步骤1)和2)，可以容易地给出级别划分算法的程序框图。给定n阶可达性矩阵CD后，公式R(capi)=R(capi)∩A(capi)等价于

dij≤dji，j=1，2，…，n

(8)

满足条件(8)的能力为最上级能力，将这些能力对应的行和列从CD中暂时划掉，从而获取一个低阶矩阵，反复使用条件(4)、(5)，便能够让各个级别的能力区分开来。

3.3 同一级别的能力关键度比较

在前文中，对能力依赖关系进行级别划分，来明确各能力之间的层次关系，还可对同一级别的能力关键度进行比较，进而得出同一级别各能力重要程度。本文对能力的比较是对体系当前状态的能力进行分析，所以认为与时间没有关系。

在作战过程中有大量的信息和数据交换，而且都是定向的，由此在作战活动网络图中形成了一条条的环路，类似于OODA环的环路。作战活动网络图与普通的网络图虽有许多相似之处，但也存在诸多不同。利用判定普通网络图中关键节点方法来判断作战活动网络图的“关键节点”明显是行不通的[7-8]，故本文围绕如何确定活动网络图中的活动的关键程度展开了研究。

本文利用活动所经过环路的数目来确定活动的环路值，同一活动经过环路的数目越多，其环路值越大。对活动的环介数进行定义：定义为活动自身经过环路的数目与所有活动中经过环路最多的数目的比值，符号为CL，值域为[0，1]。当某一作战活动环路值为1时，即表示在整个活动网络图中，其经过的环路数目最多；当某一作战活动环路值为0时，即表示在整个作战活动网络图中，其经过的环路数目为0。

利用上文中环路查找算法找出活动网络图中所有活动所经过环路的数目，即可确定活动的环介数，环介数越大，说明其关键度越大，即对体系起重要作用的程度越高。可认为该活动所对应的能力在同一级别的能力中关键度更高，即重要程度更高。

4 案例研究

假设某装备体系中含有三项任务，由前文所述的对能力活动的建模方法，分别对这三项任务进行层次分解，根据其分解关系，逐层建立分能力或子能力指标。建立其活动模型，如图4所示。

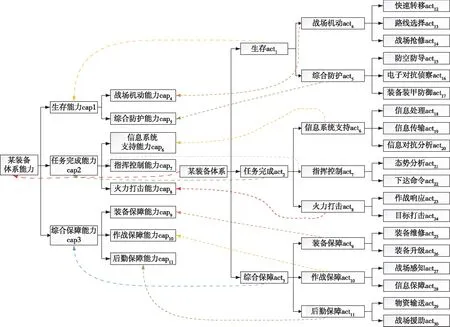
图4 某武器装备体系任务与能力关系图

其中，该武器装备体系最终可分解为30个活动，记所有活动集合为SA={acti，1≤i≤30}， 可相对应分解得到11个能力，记所有的能力集合为SC={capi，1≤i≤11}。

表4 底层能力之间依赖关系矩阵

对该关系图进行级别划分，发现所有能力都在同一级别，即每个能力的重要性一致。可得出结论，底层能力之间相互依赖，不能缺失某一能力，否则其他能力会受到影响。找出该关系图其中所有环路，并对各能力关键度进行比较，结果如表5所示。可知cap8火力打击关键度最高，重要程度最大，cap9装备保障关键度最低，重要程度最小。

表5 各能力环路数与关键度

图5 底层能力依赖关系图

根据底层能力依赖关系图，利用能力分解关系矩阵CCC，进而得出所有顶层能力间的相互依赖关系，见表6。

表6 顶层能力之间依赖关系矩阵CD

进一步分析发现，所有顶层能力都在同一级别，即每个能力的重要性一致。可得出结论，顶层能力之间相互依赖，不能缺失某一能力，否则其他能力会受到影响，且都在同一环路中，关键度相同。

5 结束语

本文建立能力概念模型以及提出对体系能力建模的一种方法，构建了体系的活动模型并利用模型对能力和活动关系进行分析。根据活动及活动间的信息交互关系，建立活动网络。利用能力分解关系矩阵，进而得出所有不同层次能力之间的依赖关系。可对能力依赖关系进行级别划分，来明确各能力之间的层次关系，还可对同一级别的能力关键度进行比较，进而得出同一级别各能力重要程度。