平面简谐波波函数中相位演变的“上下游”理解法

李泽朋 周青军 魏通 杜明润

(中国民航大学理学院 天津 300300)

大学物理的授课过程中，平面简谐波波函数的理解和掌握是重要的知识点，是学生们学习过程中容易出错的知识疑点，该知识的理解对后续波的叠加、驻波以及波的干涉等知识学习至关重要，这要求学生更方便和高效地掌握平面简谐波波函数的求解方法[1～3].

平面简谐波的波源振动为简谐振动，该振动在均匀各向同性介质中沿单一方向传播，传播方向上各处介质重复波源振动形式，仅相位与波源不同.在讲授求解平面简谐波波函数时，一般给定振源的振动方程；或在已知传播方向上，给定某一参考点(如坐标原点)的振动方程，利用任意点与参考点间相位超前或落后，求得任意一点的振动函数，即平面简谐波波函数[3～6].但比较任意点与参考点间相位超前或落后问题对部分学生稍显抽象，不易深刻理解.为方便理解平面简谐波波函数求解过程中相位超前或落后问题，本文提出将相位演变行为与 “河流上下游(相位河)”形象地对应起来，可以方便理解相位的超前或落后行为，同时弱化传播方向在波函数求解过程中的影响，可方便快捷地理解和求得平面简谐波波函数表达式.

1 “相位河上下游”理解法用于平面简谐波波函数求解过程的相位演变

波传播方向上质点相位各不相同，相位反应了各点振动与波源(或已知参考点)相比振动的超前或落后关系.假定平面简谐波在各向同性均匀介质中传播，且传播过程中没有能量损失(传播介质不变)，只需求解得到任意点与参考点间的相位差即可求解得到任意点平面简谐波波函数.因此，为便于理解平面简谐波传播过程的相位演变问题，将波沿传播方向的相位演变形象地看做“相位河”的流动.特别强调的是，“相位河”的流动是平面简谐波在传播方向上相位演变的形象化对应，并不意味着波传播过程中参与振动的各处质点元沿传播方向“流动”.利用“相位河”形象理解法，在求解平面简谐波波函数过程中，可以根据“相位河”上下游间的形象差别关系，方便地求出任意点与参考点间的振动早晚或相位差别，进而方便地写出待求任意点平面简谐波波函数.

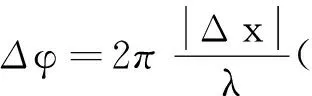
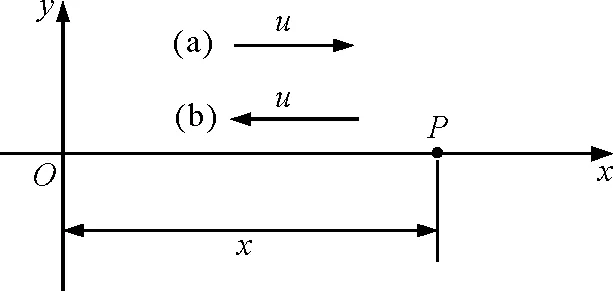
图1 平面简谐波传播示意图

一平面简谐波(横波)在各向同性均匀介质中沿x轴传播(图1)，已知坐标原点O的振动方程为

y=Acos(ωt+φ)

(1)

按照前述提到的“相位河上下游”形象化理解方式，(a)向右传播时任意点P与参考点(已知点)O相比，在“相位河”中位于已知点O的“ 下游”，P点振动晚于参考点O，则在参考点O的振动方程式(1)相位部分减去落后的相位差

(2)

(|Δx|为参考点传播到P点的距离)，即得到P点振动方程

(3)

(b)当波向左传播时，任意点P与参考点(已知点)O比较，在“相位河”中位于已知点O的“上游”，P点振动早于参考点O，需在参考点O的振动方程式(1)相位部分加上超前的相位差式(2)，可得到任意点P点振动方程

(4)

式(3)和式(4)即为任意点P(右传/左传)波函数.

上述示意题目模型较为理想，因此“相位河上下游”形象化理解并求解波函数过程，表面看来没有方便许多，但后续例题将会展示该方法在求解波函数中的快捷作用.该方法不仅可以形象化理解相位超前/落后关系，同时该形象化方法还可以降低波函数求解过程中波传播方向的分类要求(例2有涉及)，因此属于简单、实用、形象化方法.在平面简谐波波函数的学习过程中，涉及的题目类型多样，可在不同情形下使用该方法.

2 例证

【例1】一平面简谐波以速度u=20 m/s沿x轴正向直线传播,如图2所示，波长为10 m，已知A点简谐运动方程为

yA=3×10-2cos(4πt)

(5)

y,t单位分别为m,s. 若以B为坐标原点，表达出该波的波函数.

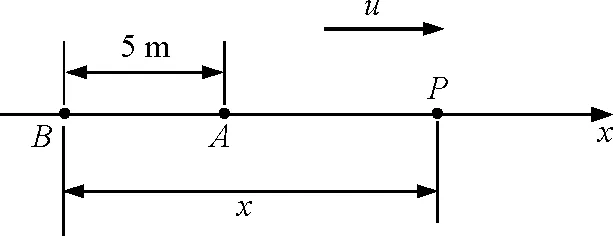
图2 平面简谐波传播示意图

分析解答：按照参考书常见的求解过程，波向右传播，A点与B(坐标原点)点相比相位落后，计算B点相位超前A点

(6)

得到B点的振动方程为

y=3×10-2cos(4πt+π)

(7)

此方程即为参考点(原点)的振动方程. 依据该波沿x轴正向传播，将任意点P坐标带入相应标准方程

(8)

便得到任意点的振动方程即为该平面简谐波波函数.

上述求解过程的思路为先求出原点(参考点)B的振动方程，结合波传播方向，将任意点坐标x带入标准方程，即得到波函数方程.

若采用前述介绍的“相位河上下游”理解法，经判断，任意点P位于“相位河”中已知点A的“下游”，P点振动与已知点A相位差为

(9)

依据“下游点”减去相位差，将已知A点振动方程式(5)相位部分减去式(9)，即可得到任意点P的振动方程

(10)

(11)

即为任意点波函数.利用该方法求解过程较为简单.

“相位河上下游”理解法在求解含反射情形下反射波函数时，更为方便.

【例2】如图3所示，一列波以波速u沿x轴正向传播，已知原点O振动方程为

y=Acos(ωt+φ)

(12)

距离原点L处有一墙面(反射面M)，求反射波在P点的波函数(墙面反射时，无能量损失，但存在半波损失).

图3 平面简谐波入射和反射传播示意图

分析解答：按照参考书的常见求解流程，考虑入射波向右传播，根据原点O的振动方程式(12)，入射波传播方向上任意点P的振动方程为

(13)

该波继续向右传播到M点，将M点坐标代入，得到入射波M点的振动方程为

(14)

波在M点反射后由于存在半波损失，因此反射波M点的振动方程为

(15)

之后该波向左传播.

(16)

化简得到其振动波函数为

(17)

考虑到P点的任意性，式(17)即为反射波的波函数.

若按本文提出的“相位河上下游”理解法：不论传播方向向左或是向右，反射波中P点的相位与已知点(参考点)O相比位于“相位河下游”，因此与参考点O的振动相比，其相位落后；按照总共传播距离(“相位河”相位演变)来计算(下游方向)相位落后.从O点传播到M点，再反射至P点，共计传播距离为(2L-x), 考虑到中间反射一次，因此具有附加相位差π，反射波到达P点后，P点最终的振动函数为

(18)

式(18)即为P点的反射波函数.

因此，采用该理解方式求解此类习题时，过程较为简单便捷，且因反射引起的传播方向改变时也可以简单处理.

3 结束语

“相位河上下游”法是笔者教学实践中提出的一种处理简谐波问题的教学方法，它可以形象化理解波传播中的相位超前和落后关系，且在等效求解过程中对波传播方向分类要求低，求解过程中可忽略不同波传播方向的区别或传播方向的改变.在面对复杂问题(如反射波)时，弱化了波传播方向在求解波函数过程中的影响，将传播方向这一影响因素与相位的超前与落后归结在一起，可将理解平面简谐波波函数的求解过程变得形象化和简单化.