Mathematica在大学物理教学中的应用举例*
赵文丽 高峰 王永刚 曹学成
(山东农业大学信息科学与工程学院 山东 泰安 271018)
1 引言
大学物理是理工农林学科学生必修的一门基础课,每年都会有大批的大学一二年级的学生学习这门课程.作为一门公共基础课程,大学物理有其自身的特点:一方面,大学物理问题的解决涉及到许多高等数学方面的计算,求解过程复杂,有些情况没有解析结果,也往往不能得到直观的物理图像,这是不利于教学过程的;另一方面,基础物理课内容多,学时少,每节课授课内容量都很大,很多知识点不能深入讲解.近年来更是面临着学时一再被压缩的窘境,这就导致学生从课堂中获取的知识量大为减少.因此,物理教师必须寻找一些新的教学方法,以期在有限的课堂时间里向学生传递更多的信息.美国Wolfram公司生产的一款数学软件Mathematica在设计的过程中考虑了在物理学方面应用的方便性[1],很适合研究物理问题,它强大的计算功能和图像功能可以用于辅助物理教学与研究.比如董键主编的一部教材讨论了Mathematica在力学、光学、电磁学等方面的应用[2].柳宏德用Mathematica获得了任意摆角下的单摆周期近似公式[3].杨能彪应用Mathematica进行物理理论计算和物理现象可视化的研究[4],获得了一些有意义的结论.本文则试图通过Mathematica设计力学、电磁学中一些问题的解决方案,探索Mathematica在大学物理教学中的应用.
2 单摆的小角问题
单摆模型是力学中很重要的物理模型,普通物理教材中提到[5],在小角度摆幅下,单摆的运动近似为简谐振动,其周期、振幅等物理量有精确的解析解,并且周期与振动振幅无关.那么究竟这个“小角度”需要小到什么程度呢?现在可以利用教学软件Mathematic来探索这一问题.
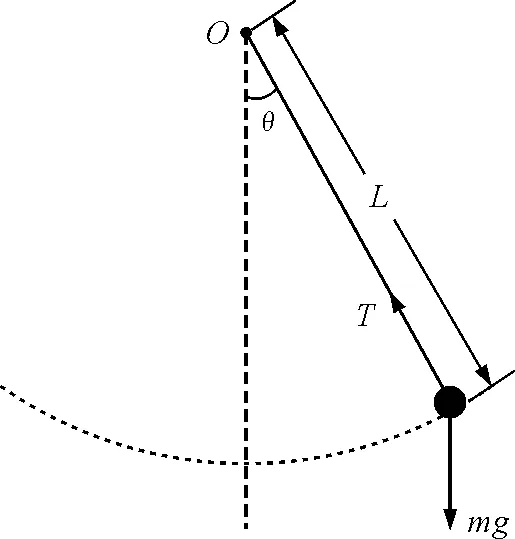
图1 单摆模型
设系统所在的地球为惯性参考系,摆线不计质量且不可伸缩(如图1),单摆的摆长为1.5 m,重力加速度取9.8 m/s2.采用自然坐标系,摆线在竖直方向时摆角取零,摆球在右侧摆角取正,切向正方向为摆角增大的方向,考虑摆线带动下摆球在竖直平面内的运动,显然小球没有沿着摆线所在的法线方向运动,而在其垂直的切线方向,切向力为
Gτ=-mgsinθ
切向加速度可以表示为
则根据牛顿第二定律有摆球的运动方程
maτ=-mgsinθ
(1)
两边消去小球质量可得
(2)
在小角近似下,sinθ≈θ,该方程有解析解,可以得出周期公式
(3)
如果摆角为任意的角度,单摆的周期也不再有解析解,那么小角近似的周期公式便不再适用了.要求解微分方程(2),用Mathematica的“NDSolve”命令即可,因为它就是专门求解微分方程的数值解的工具.从数值解容易得出不同初始条件下的振幅和周期.如输入初始位置θ=0,初速度v=0.3 m/s,可得,角振幅和周期的数值解分别为0.067767°和2.839 27 s.输入不同的初始条件,就可以得出对应的角振幅和周期.为此,可以求出在摆动角振幅从0~90°范围内对应的周期的数值解,同时,为了能够精确找到周期满足公式(3)的小角近似的定量条件,可以对数值解进行n(n=4,5,6,7)次多项式拟合,取若干不同的角振幅对应周期的数值解和拟合解相比较如表1所示.从表1中所取的6种情况可以看出,n=4,5时,某些角振幅下拟合值与数值计算解不能完全吻合,而n=6,7时,二者则完全吻合,因此,拟合多项式的次数取6已足够.拟合公式为式(4).
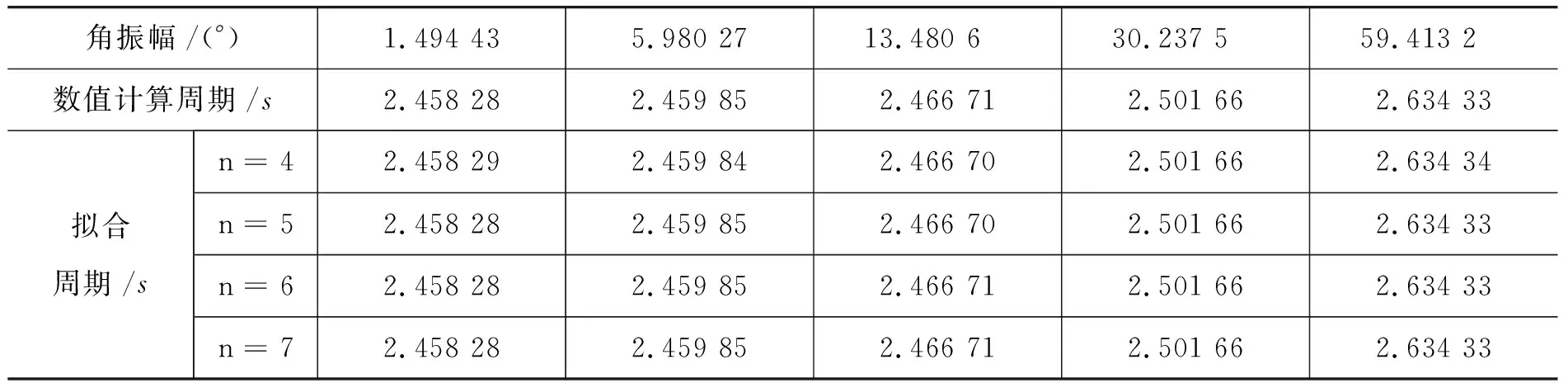
表1 不同角振幅对应周期的数值解和拟合解
T=2.458 18-2.814 99×10-6θ+4.717 02×
10-5θ2-2.044 44×10-8θ3+1.365 28×10-9θ4-
7.230 52×10-12θ5+5.550 18×10-14θ6
(4)
图2是周期随着角振幅变化的关系图,圆点是数值解,曲线是拟合公式所得,从图中可以看出数值计算点与拟合曲线符合得非常好,要计算任意角振幅对应的周期,可以用该拟合公式.

图2 单摆周期随角振幅的变化
另外,图2还表明周期是随着角振幅的增大而增大的,尽管变化是很缓慢的.那么究竟角振幅要小到多少之内,周期就不会变化了?基于这样的疑问,可以用拟合公式计算相同初始条件下的周期,再与数值计算的结果相比对,表2列出了若干角振幅在0.1°到1.2°对应的周期,结果发现,角振幅小于0.5°时,周期便不再变化,该体系做简谐振动.
所以,从计算所得到的6位有效数字来看,0.5°以下才算是小角度.这样,关于单摆“小角度”的说法获得了定量的表示.但是,有的物理教材认为这个角度可以是15°甚至可以超过20°[6,7],这是因为,基础物理实验室用来测单摆周期所用的秒表,精度为0.01 s,计算发现如果取这样的精度,角振幅在10°以内周期完全相同,即使角振幅达到20°,误差也不会超过0.1%.

表2 0.1°~1.2°之间不同角振幅对应的周期
3 均匀带电细圆环全空间的电势分布和场强分布
均匀带电细圆环是静电场的一个重要的物理模型.如图3所示,设环的半径为R,环的电荷线密度为λ(λ>0),根据带电圆环的对称性,选择柱坐标如图3所示,设环心位于O点,带电圆环在Oxy平面,φ是圆环上任意点P′与O点的连线P′O与y轴之间的夹角.空间任意一点P距离Oxy平面为z,与z轴的距离为ρ,P所在的与z轴垂直的平面上距离z轴相等的点电势相同,所以可以认为P点就在Oyz平面上,坐标为(0,ρ,z),根据电势叠加原理,P点的电势是圆环上所有电荷在该点产生的电势之和
(5)
令
R2+z2+ρ2=a 2Rρ=b
则得到
(6)
该式中的积分为椭圆积分,其结果可以用Mathematica内置的椭圆函数表示
(7)
令
得到电势全空间的分布如图4所示,从图中可以看出,在靠近线圈的位置即(0,ρ,z)=(0,1,0),电势有极大值,其他位置电势依次降低,距离线圈很远的位置,电势为零.在线圈内部的平面内,电势比线圈外部高.
考虑到电荷分布的对称性,可以先计算Oyz平面内的电场分布,因为电场强度矢量与电势的微分关系为
(8)
根据式(8)画出的Oyz平面内的电力线如图5所示.

图5 均匀带电细圆环在Oyz平面内的电力线
很显然,电力线关于z轴对称,将y>0或者y<0范围内的电力线绕z轴旋转任意角度就可以得出空间其他位置的电力线.
最后,取z轴这个特殊的位置进行计算,可以得出通过圆环中心轴上的场强分布和电势分布如图6所示.

图6 均匀带电细圆环中心轴的电场强度和电势分布
以上应用Mathematica处理均匀带电细圆环的电势与电场强度问题的过程是先计算全空间的整体分布,再具体到轴线上.解决问题的过程可以加深学生对电场强度和电势这两个物理量以及二者之间关系的理解,其结果用图像的形式表示出来,使学生能够从整体上把握该体系的电场强度和电势分布.这种由一般到特殊的方法好处在于能让学生在处理物理问题的过程中着眼于大局,从更高的层面去分析问题.
4 结论
本文用Mathematica软件对力学和电磁学中两个重要的物理模型进行了深入的研究,给出了单摆小角度的定量解释以及均匀带电细圆环全空间的电势和电场强度分布.这种探索对于教师教学过程以及学生学习过程是非常有益的,而且通过编程计算作图的结果可以直观呈现给学生,加深学生对知识点的理解,提高课堂效率.物理学的问题五花八门,层出不穷,而Mathematica软件的计算和绘图功能强大,所以,Mathematica在物理问题的研究以及辅助物理教学方面的应用前景是非常广阔的.

