扩散声场作用下C/SiC复合材料薄壁结构的全频段响应分析
张永杰,陈利斌,张菩仁,王 喆
(1. 北京强度环境研究所,北京 100076; 2. 中国船舶工业系统工程研究院,北京 100094)
0 引言
航天器在飞行过程中会受到严酷的噪声载荷作用[1-2],其主要来源包括发动机的喷流噪声和湍流边界层引起的脉动压力噪声。前者主要在发射和起飞阶段产生,后者则是再入、巡航阶段最重要的噪声来源。噪声载荷会引起结构振动和交变应力,不仅会影响航天器重要仪器设备的正常工作,而且会导致结构的疲劳破坏[3]。新一代航天器中大量采用复合材料,使得声致振动频带宽(10 Hz~10 kHz)、量级大,因此,进行大量级、宽频带噪声载荷作用下的结构全频段应力场分析,并通过结构设计加以控制具有非常重要的意义。
声振响应计算方法主要有边界元法、有限元法、统计能量法以及混合模型法等。用有限元法和边界元法进行时域分析可得到结构具体位置的位移、速度、加速度以及应力等动态响应结果。但航天器所经历的声振环境覆盖整个高中低的全频段,使用有限元法和边界元法进行计算时,一方面模型的单元数量会随着频率的增大而急剧增加,导致计算成本过高;另一方面有限元法和边界元法是基于结构的确定性物理参数,而实际工程结构的真实参数与其名义参数有所不同,且高频振动时结构对于物理参数微小的变化都非常敏感,会导致计算结果与真实响应结果间存在较大的偏差。因此,有限元法和边界元法并不完全适用于全频段的声振响应分析[4]。统计能量法(SEA)主要用来预测噪声激励下的结构振动响应及内部噪声情况,弥补了有限元法在声振响应分析领域的不足,主要应用于结构振动响应的高频段分析[5-6]。为了进行全频段的声振响应分析,混合模型方法的研究逐渐兴起[7-8],其中有限元-统计能量混合模型法(hybrid FE-SEA method)与其他方法相比具有更广泛的工程适用性和发展前景,已成为声振分析的一种有力工具[4,9-10]。
统计能量分析中的变量是子系统的振动能量,主要依赖于子系统的振动速度均方根值,因此,使用有限元-统计能量混合模型进行声振响应分析,主要是计算结构的加速度响应[9-12],关于声振的应力场分析研究较少。而复合材料与各向同性材料的力学本构关系不同,其声振应力场分析颇为复杂。这些均给通过声振应力场进行航天器疲劳分析的研究带来困难。
本文着眼于扩散声场作用下复合材料薄壁结构的全频段应力场分析,在混响室内进行自由状态下的C/SiC复合材料薄壁结构的噪声试验;建立扩散声场与正交各向异性复合材料薄壁结构相互作用的有限元-统计能量(FE-SEA)混合模型;基于模态应力恢复方法获取结构应力场分布结果并进行分析。
1 模态应力恢复方法
在模态空间中,结构的位移可由模态振型及模态坐标的线性组合表示为[13]
式中:M、C、K分别为质量矩阵、阻尼矩阵和刚度矩阵;q为模态坐标;为模态振型。
根据模态应力恢复理论,随机载荷下的模态响应可以模态互谱矩阵Sqq表示为[13]
式中E代表平均。若考虑n个模态,则Sqq(ω)为n×n阶矩阵。
假设在有限元某节点i上,力和应力等响应量的个数为m,则它们的均方值响应为

式中pi表示节点i上的模态坐标矩阵,为k×m阶矩阵。
如果求得有限元模型中某节点的模态应力矢量为
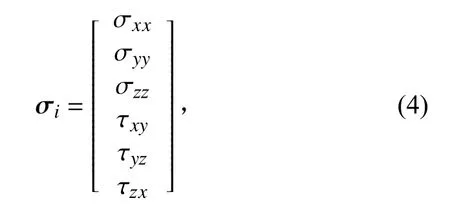
则Von Mises应力的RMS值为

式中:trace表示矩阵的迹,定义为矩阵对角线上的元素之和;对称矩阵A的定义为

式中sym表示A的对称元素。
2 混响室噪声试验
整个噪声试验系统由混响室、气源、声源、声谱控制、声测量和结构响应测量6个主要子系统组成。试件为厚度1.5 mm的C/SiC复合材料薄壁结构,长380 mm、宽260 mm,通过橡皮绳悬吊在70 m3混响室内,模拟自由边界条件。C/SiC复合材料为正交各向异性材料,其力学性能参数如表1所示。

表1 C/SiC 复合材料力学性能参数Table 1 Mechanical parameters of the C/SiC composites
在复合材料平板上布置3个振动传感器进行平板的声振加速度响应测量,以平板的几何中心为原点,3个加速度测点的坐标分别为(40, 95)、(-40,-95)和(45, -95),单位mm。在平板的附近和周围布置传声器,进行声场测量。试验设备及测点位置如图1所示。混响室噪声试验中加载的总声压级为140 dB,在声载荷以及结构响应稳定后,测量混响室内扩散声场以及C/SiC复合材料薄板上的振动加速度响应。混响室内传声器获取的声谱如图2所示。

图1 C/SiC复合材料薄壁结构的混响室噪声试验Fig.1 Experiment of C/SiC composite thin plate structure in the reverberant chamber
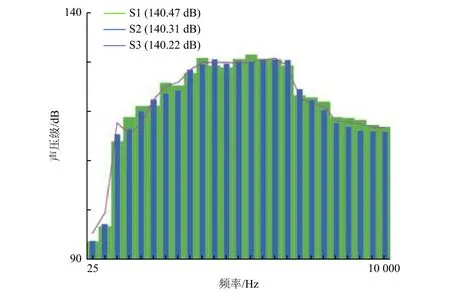
图2 140 dB噪声载荷下声场测点声谱Fig.2 The sound spectrum of the diffusive sound field (SPL=140 dB)
3 FE-SEA混合模型
使用正交各向异性材料本构关系,建立1.5 mm厚C/SiC复合材料薄壁结构的有限元模型并求解模态。模态频率的试验结果与计算结果如表2所示,各阶模态振型的试验与计算结果较为吻合,表明该有限元模型在低频段是准确的。
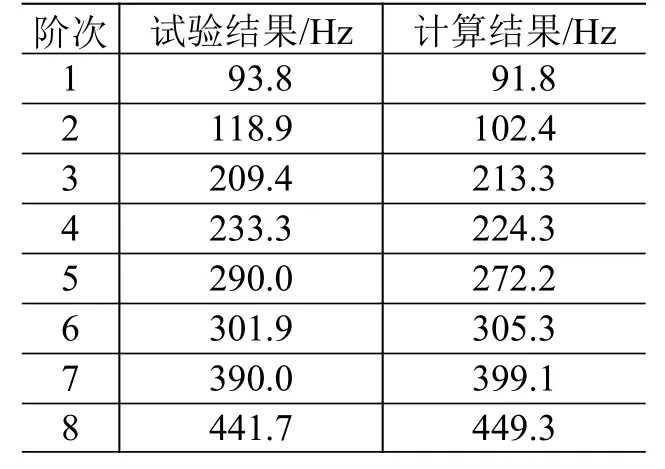
表2 自由状态模态频率试验与计算结果对比Table 2 Comparison between the tested and calculated modal frequencies under free boundary conditions
对混响室内3个传声器获取的声谱求平均,作为声载荷(如图3所示)。在VA One软件中使用有限元子系统对薄壁结构进行建模,使用半无限流体(SIF)统计能量子系统对声辐射的空气进行建模,使用扩散声场(DAF)进行声载荷施加。最终建立的扩散声场环境下的FE-SEA混合模型如图4所示。
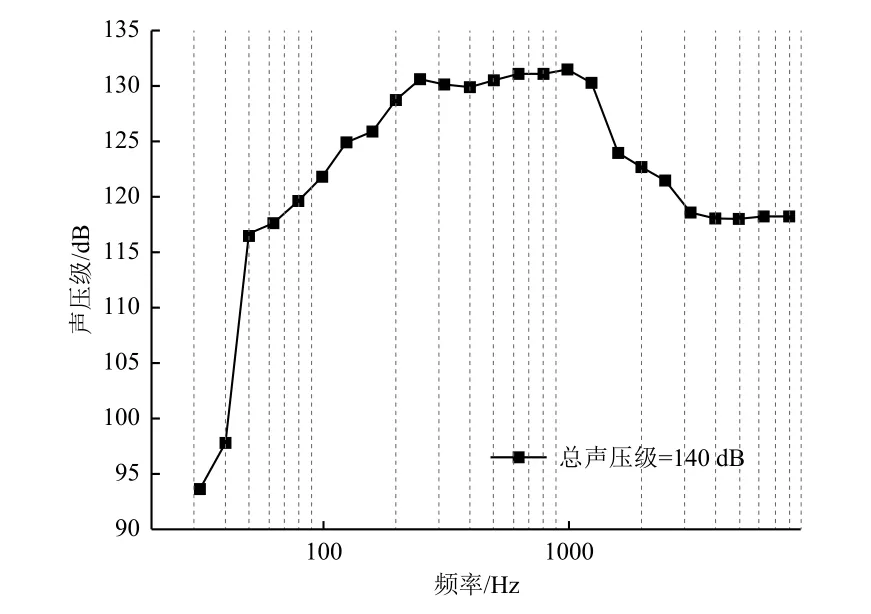
图3 扩散声场载荷Fig.3 Loading of diffusive sound field

图4 混响室噪声试验的FE-SEA混合模型Fig.4 Hybrid FE-SEA model for acoustic test in the reverberant chamber
4 应力场及加速度响应结果分析
计算得到薄壁结构8000 Hz以内的加速度响应均方根分布云图如图5所示,可以看出:除了4个尖角位置的响应最大外,板的边沿和中心区域的振动响应也较大,其加速度均方根值在9g~14g之间,其他区域则在5g~9g之间。计算结果与试验结果吻合。
图6所示为加速度测点3和对应位置的计算功率谱密度的对比曲线,可以看出:在整个分析频率范围内,2条曲线的变化趋势以及峰值位置一致,但在100 Hz以下差别较大。这是由于试验测试中结构悬吊边界引起结构整体的振动响应。
图7所示为基于模态应力恢复方法计算的扩散声场作用下C/SiC复合材料薄壁结构的应力场分布云图。其中Mises应力均方根值的最大和最小值分别位于平板的短边中央和四角。通过图5与图7的比较可以看出,扩散声场作用下的复合材料薄壁结构的应力场分布与加速度场分布规律并不相同。

图5 加速度响应均方根值分布云图Fig.5 Cloud map of root mean square value of acceleration response
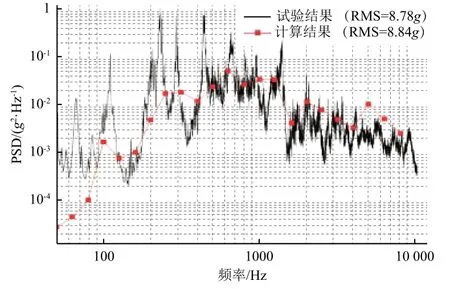
图6 加速度响应计算与试验结果对比Fig.6 Comparison between the simulation result and the experimental result of acceleration response
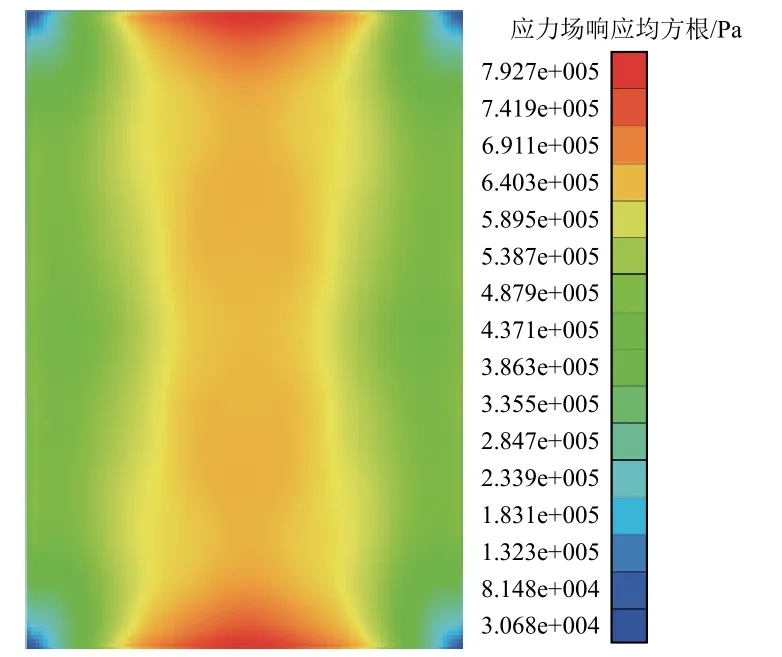
图7 应力场响应均方根值分布云图Fig.7 Root mean square value field of the Von Mises stress
图8所示为噪声场声谱、声载荷到结构的输入功率以及结构辐射到空气中的功率曲线。可以看出:相对于扩散声场载荷,结构吸收的功率在以100 Hz为中心频率的频带内有1个峰值,并且在1500 Hz以后吸收声能较多,在以5000 Hz为中心频率的频带内有1个峰值。表明结构在以100 Hz为中心频率的频带内吸收功率较多,而辐射功率很小,从而形成响应峰值。结构辐射到空气中的功率在以5000 Hz为中心频率的频带内出现了峰值,表明在该频带内结构不仅能从声场中吸收大量能量转化为结构的振动能量,而且向空气中辐射较多声能量,即该频带内声场与结构的波长耦合效应最强。
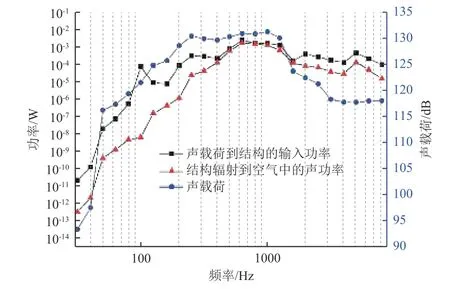
图8 扩散声场声谱、声载荷到结构的输入功率以及结构辐射到空气中的声功率曲线Fig.8 The sound spectrum of the DAF, the power input of DAF to the structure, and the structure's acoustic radiation to the SIF

式中:B为弯曲刚度,B=Eh3/[12(1-ν2)],其中,E为弹性模量,h为薄壁厚度,ν为泊松比;ω为圆频率;ρ为材料密度;fc为临界频率。
C/SiC薄壁结构的振动以面内弯曲振型为主,将C/SiC薄壁结构的厚度和材料参数(弹性模量E1和泊松比 ν13)代入式(7),计算得到临界频率为5262 Hz,处于以5000 Hz为中心频率的频带内。说明在临界频率处,结构振型能够与声场发生很好的耦合,结构不仅能从声场中吸收大量能量,而且能向空气中辐射较多声能。
5 结束语
本文针对扩散声场作用下复合材料薄壁结构的全频段应力场分析问题,在混响室内进行自由状态下的C/SiC复合材料薄壁结构的噪声试验;建立了扩散声场与正交各向异性复合材料薄壁结构相互作用的有限元-统计能量混合模型;并基于模态应力恢复方法计算得到了结构的应力场分布;通过分析复合材料薄壁结构的弯曲波长与声波波长之间的关系,揭示了噪声载荷与结构的波长耦合效应。
研究结果表明:模态应力恢复方法可用于全频段声振应力场分析的FE-SEA混合模型中,该模型计算的应力场可进一步用于声疲劳分析。

