满足高铁桥梁双重性能需求的新型减震装置研发及力学性能研究

李雪红， 孙 磊， 徐秀丽， 王 蕊

(南京工业大学 土木工程学院，南京 211816)

从以往的地震灾害可知，高铁的事故率偏高。在青海玉树地震中，40%以上的铁路桥梁出现了轨道折角，可能导致高速运行的列车发生脱轨事故[1]。2008年的汶川地震之后，中国铁道学会召开了“地震灾害对铁路的影响及对策”学术交流会。与会专家普遍认为，我们应从传统的“抗震”设计理念中走出来，应该用“减隔震”的设计理念来代替以往的抗震理念[2]。

采用减震装置减小地震响应的优点目前已被无数专家学者肯定。最早提出减隔震概念的是在1881年,日本学者河合浩藏[3]。随后掀起了一股减隔震研究的浪潮[4-6]。很多减隔震产品被应用到建筑上后，其有效性还在实际地震中得到了验证[7]。如1994年美国Northridge地震中采用减、隔震技术设计的南加州福尼亚大学医院，震后完好无损，迅速投入抢险救灾中。

与建筑结构相比，桥梁虽引入减、隔震设计较晚，但在国内外公路桥梁结构中已有广泛发展。美国、新西兰、日本和欧洲的一些国家已将减、隔震设计纳入桥梁抗震规范中[8]。范立础等[9]概述了国外的桥梁减、隔震技术的发展，与我国桥梁减隔震技术的研究和发展进行了对比，讨论了结构采用减隔震技术的一些特点并提出了促进我国桥梁减、隔震发展的意见。普通公路桥梁中大跨度的柔性结构主要采用具有减震耗能作用的液体黏滞阻尼器、弹塑性软钢阻尼支座、LUB速度锁定支座、调谐质量阻尼器(TMD)、调谐液体阻尼器(TLD)等装置以增大阻尼，实现减小结构地震响应的目的[10-12]。目前的减隔震措施大多是针对公路桥梁或一般的铁路桥梁，针对高铁桥梁特殊的结构特性及高速运行的列车的行车安全性需求所做的研究尚较少，还缺少成熟有效的减隔震措施。

本文借鉴黏滞型阻尼器的设计思想，研发出一种适用于高铁桥梁的新型耗能减震装置(以下简称新型装置)。该装置在地震发生时，盆式支座剪断瞬间，可抵抗较大的冲击作用，提供足够的刚度，保证高铁桥梁的整体刚度不发生突变，并且控制轨道不出现较大变形和较大振动，保证高速运行的列车在地震发生时的行车安全性，并提供列车减速制动的时间；随后，该装置发挥耗能作用，减小高铁桥梁的地震响应，保证桥梁的抗震安全性。即，该装置既可以保证高速运行的列车的行车安全性，亦可以保证高铁桥梁的抗震安全性，具有双重性能。

对该装置进行耗能性能及抗冲击性能试验。通过试验，分析该新型耗能减震装置在低速稳态输入下，不同运动频率和速度对其耗能能力的影响；分析在高速瞬时输入下的抗冲击性能及冲击力相关性；提出阻尼力公式，为实际工程应用提供理论依据。

1 新型装置的设计和工作机理

本文利用结构耗能减震控制技术，结合土木工程领域应用广泛的黏滞阻尼墙和圆筒式黏滞阻尼器的设计思想[13]，研发满足高铁桥梁双重性能需求的新型耗能减震装置。其汲取黏滞流体流经节流孔产生阻尼力的液体黏滞阻尼器的优点、由黏滞阻尼材料的剪切阻抗产生阻尼力的黏滞阻尼墙的优点以及结合滚珠丝杠副的变直线运动为旋转运动的机械传动原理来进行创新构思。

本新型装置具体构造设计如图1所示，包括传递部分和阻尼部分。

传递部分如图2所示，由螺母旋转式滚珠丝杠副组成，丝杠受力时带动螺母旋转，将直线运动变成旋转运动。阻尼部分包括密封圈、阻尼筒、黏滞液体、螺钉。各阻尼筒同轴线嵌套设置如图3所示。阻尼筒奇数层与螺母相连，偶数层与另一端相连。阻尼筒奇偶层间留有间隙填充黏滞液体且间隙两侧设有密封圈确保黏滞液体处于密封环境内。阻尼部分通过螺钉与传递部分相连。传递部分的螺母通过螺钉带动阻尼筒旋转。本新型装置在耗能的同时可有效控制墩梁间的相对位移，控制轨道的变形。可通过调整阻尼筒的层数、长度、阻尼筒直径、阻尼筒层间间隙及滚珠丝杠副的螺距来改变阻尼力。

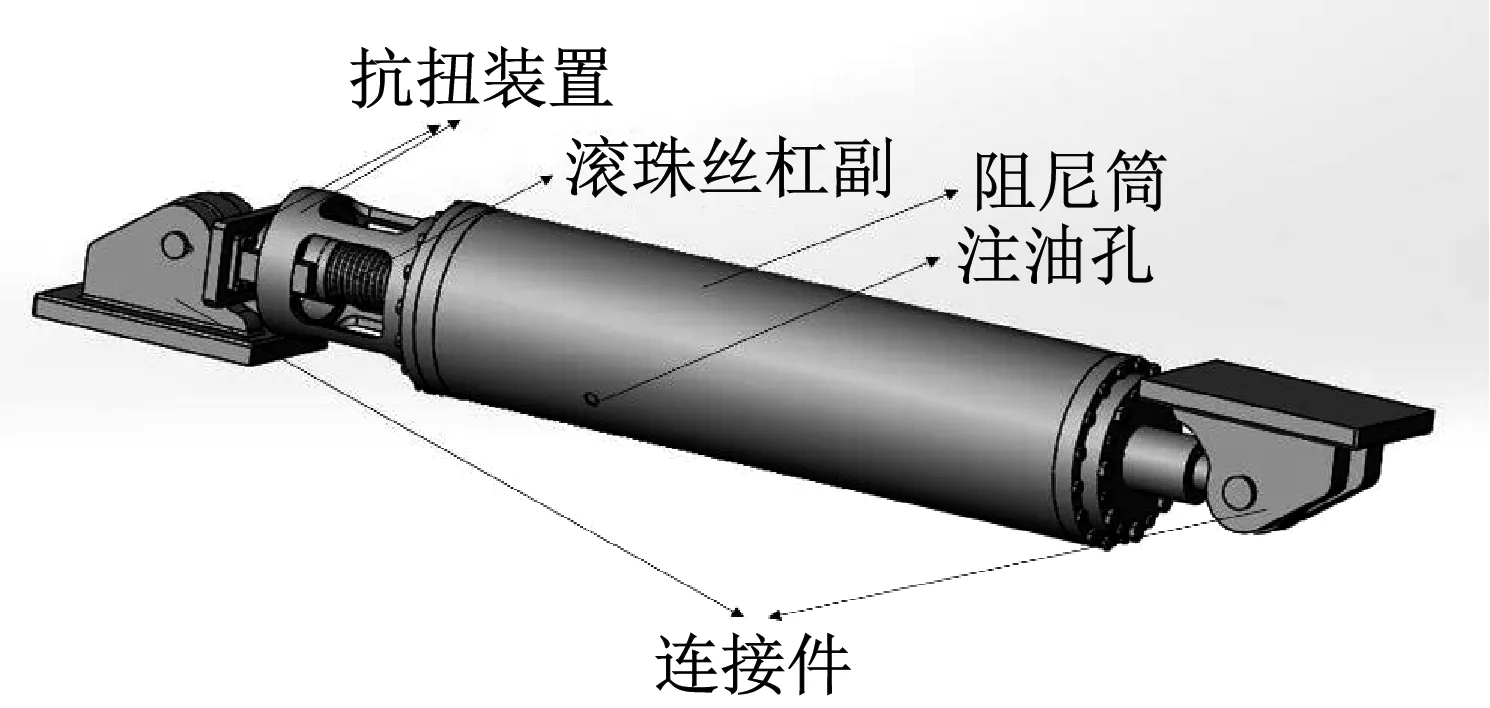
(a) 总装图

(b) 剖面图

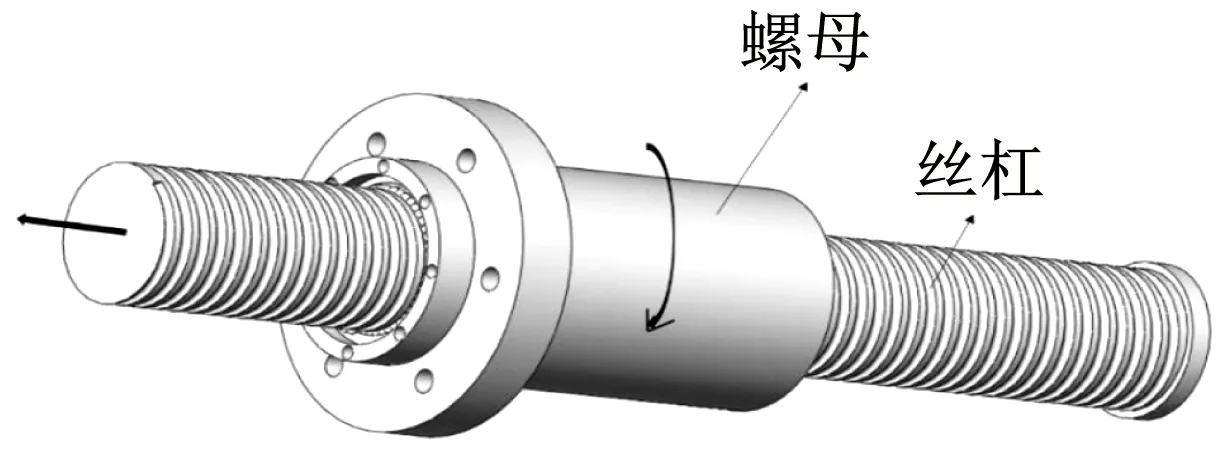
图2 原理示意图(滚珠丝杠副)

图3 阻尼筒设置

2 新型装置的耗能性能研究

2.1 试验工况

根据新型耗能减震装置的工作原理，通过设置不同的加载频率、加载速度，采用低周反复试验验证该装置的耗能能力并分析耗能能力与加载频率、加载速度等的相关性。试验工况如表1所示，图4为试验现场。

根据实验设备的实际加载能力确定加载制度。实验采用正弦激励法，位移控制加载，位移、速度与时间的关系如式(1)、(2)所示：

表1 低周反复试验加载工况

图4 实验现场

S(t)=S0·sin(2πft)

(1)

V(t)=S0·2πf·cos(2πft)

(2)

2.2 加载频率对耗能能力的影响

图5为温度保持一定(3 ℃)，不同位移幅值(2 mm、3 mm、4 mm、5 mm)时，各加载频率下的装置的滞回曲线。

由图5可知，在不同位移幅值时，阻尼力随加载频率的变化规律相似，均随着加载频率的增加而增大，以位移幅值4 mm为例，加载频率0.01 Hz、0.015 Hz、0.02 Hz和0.025 Hz对应的最大阻尼力依次为102 kN、159 kN、177 kN和235 kN。并且，滞回曲线所包围的面积随加载频率的增大亦逐渐增大，耗能能力逐渐增强；除此之外还可看出，各工况下滞回曲线均有明显倾斜且随加载频率增加，倾斜程度有一定的增大趋势，即该装置的刚度随加载频率的增加而增大。

(a) 2 mm (b) 3 mm (c) 4 mm (d) 5 mm

从实验结果可看出，所有工况的滞回曲线中均有一个1 mm长，阻尼力为0 kN的传动失效部分。这一现象的出现与本文新型装置上的扭矩平衡装置的构造设计存在一定关联。为使平衡筒不影响平衡销上下方向的自由移动，将平衡筒上销槽的宽度设置成比平衡销的宽度大1 mm。

2.3 加载速度对耗能能力的影响

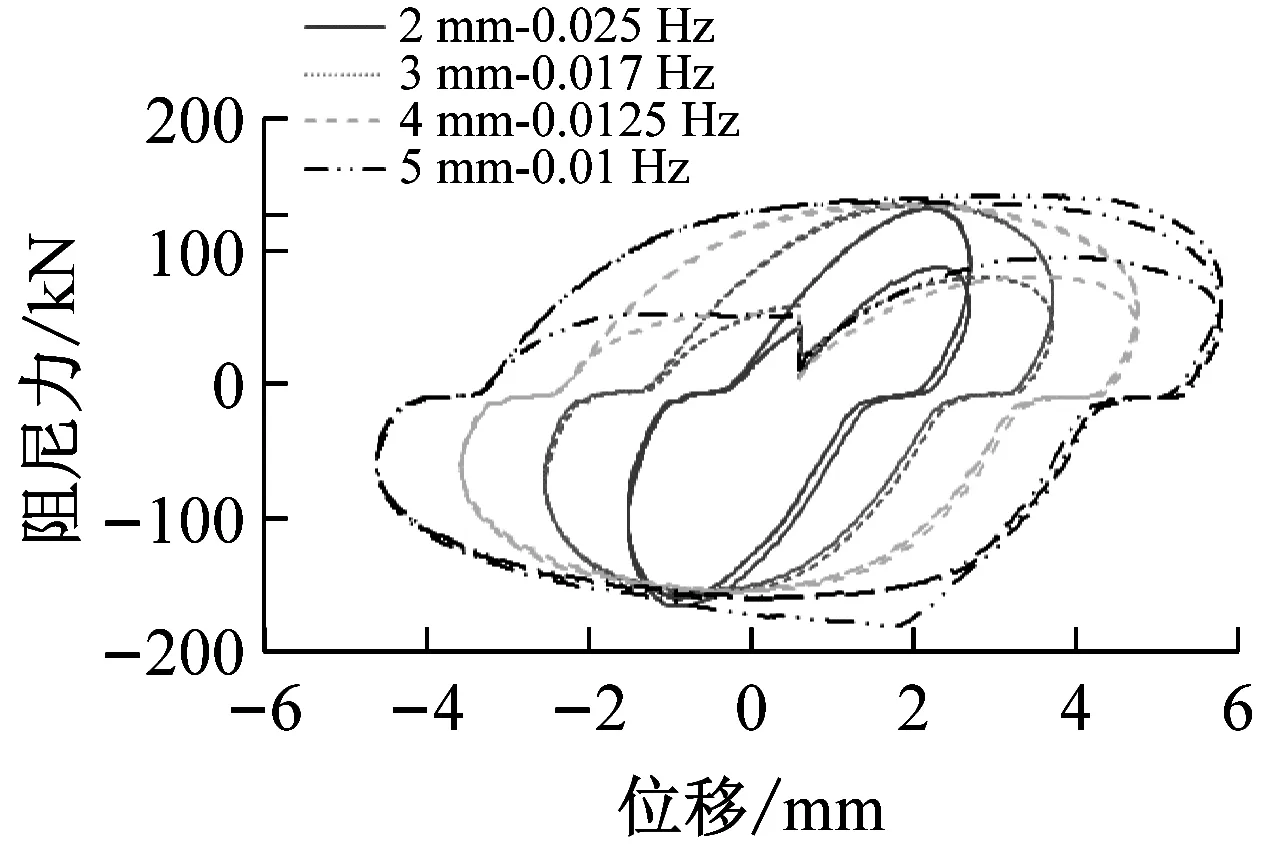
温度依然取室内温度3 ℃，最大加载速度保持Vmax=0.157 mm/s、0.314 mm/s、0.628 mm/s一定，所得滞回曲线如图6所示。

(a) Vmax=0.157 mm/s

(b) Vmax=0.314 mm/s

(c) Vmax=0.628 mm/s

由图6可以看出当加载速度Vmax保持为0.157 mm/s、0.314 mm/s和0.628 mm/s不变时，各工况下的阻尼力最大值分别保持在83～89 kN、137～141 kN和235～242 kN之间。考虑实验误差的影响，可以认为当最大加载速度保持一定时，各工况下的最大阻尼力保持一致。

除此之外，由图7还可以看出，随着加载速度的增大，该新型装置的阻尼力不断增大，当速度从0.157 mm/s增加到0.314 mm/s时，阻尼力增大64.7%，当速度从0.314 mm/s增加到0.628 mm/s时，阻尼力最大值增大71.4%。即新型装置的耗能能力随最大加载速度的增加而增大。

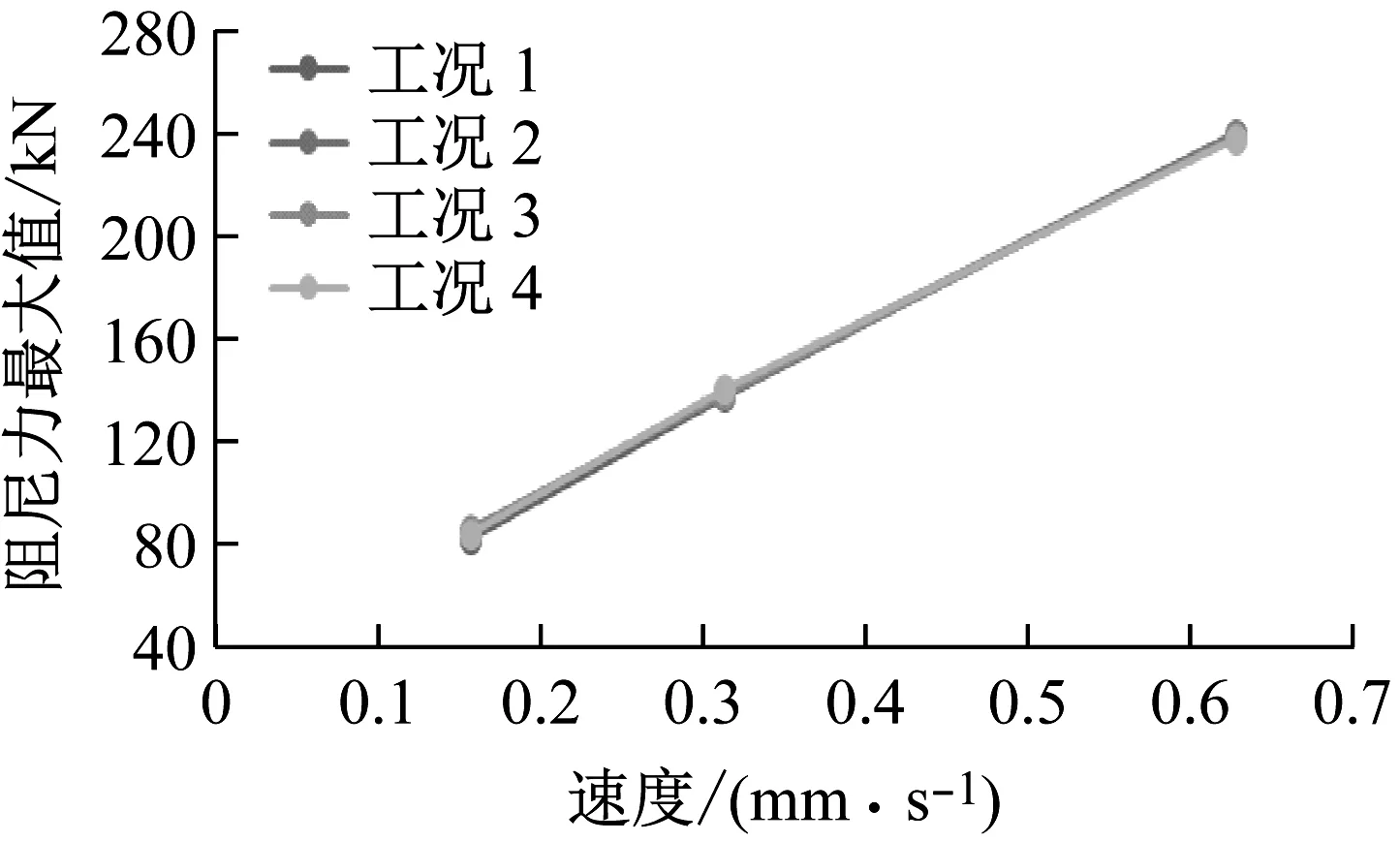
图7 不同工况下阻尼力最大值

3 新型装置的抗冲击性能试验研究

3.1 试验工况

本文的新型耗能减震装置应满足高铁桥梁的双重性能需求。首先该装置应有较强的耗能能力，减小地震发生时高铁桥梁的地震响应；其次，该装置在地震发生时，支座剪断瞬间，能够承受较大的冲击作用，并能够提供较大的刚度，使桥梁的整体刚度不发生突变，从而使轨道不出现较大变形，保证高速运行的列车能够有一定的减速时间，使之不发生脱轨或倾覆的安全事故，或降低其发生概率。因此，需要对所研发的装置的抗冲击性能及在冲击力作用下的位移情况进行深入研究。

根据新型耗能减震装置的工作原理，通过设置不同的冲击力、冲击频率来验证其抗冲击性能及位移，并分析与冲击频率、冲击力的相关性。

考虑实验设备的实际加载能力，确定每组实验工况的加载制度，实验采用正弦激励法，力控制加载，力与时间的关系表达式为：

F(t)=f0·sin(2πft)

(3)

实验工况见表2，表中F(kN)为冲击力,f(Hz) 为加载频率。

表2 冲击试验加载工况

3.2 抗冲击性能

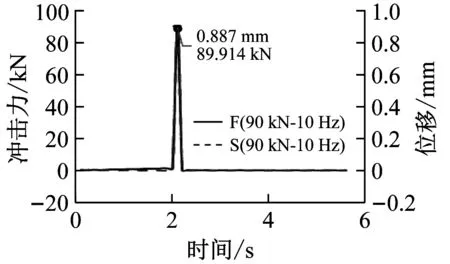
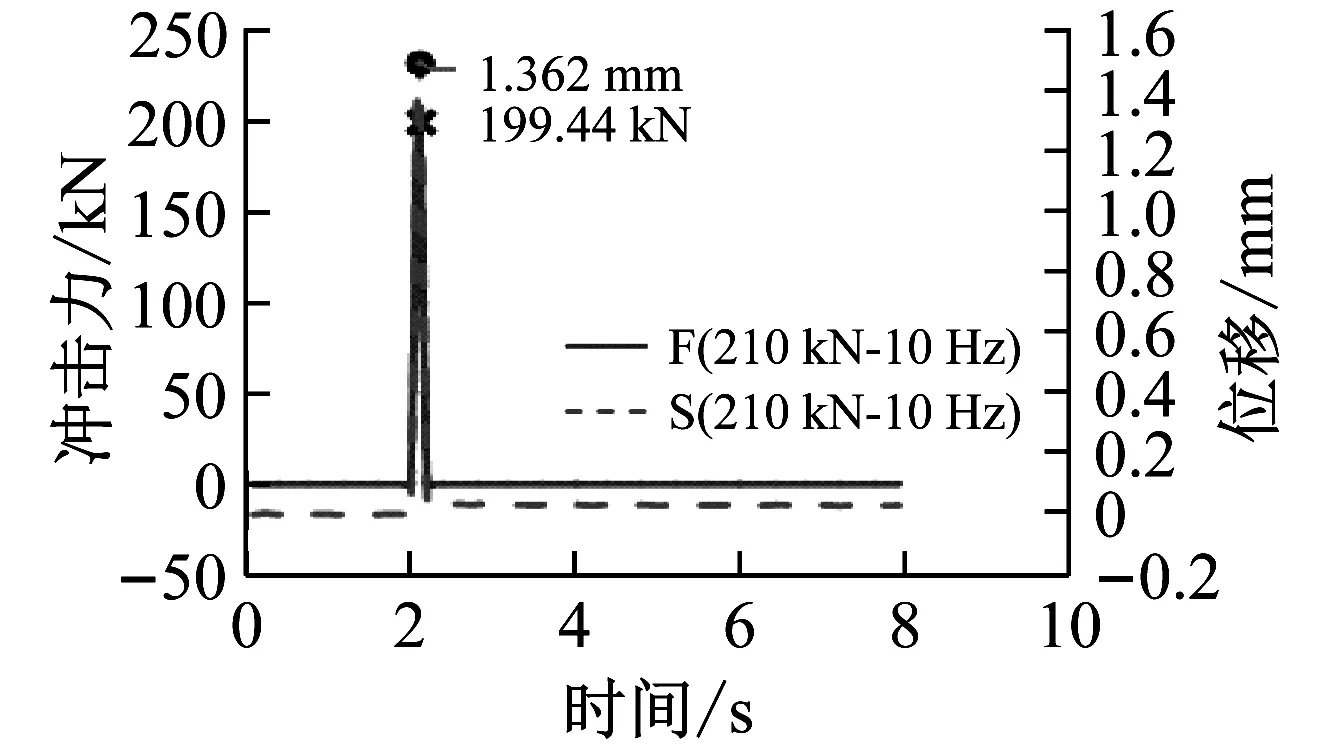
冲击实验每组工况循环两次，分别沿着上拉和下压两个方向各冲击一次。若两个方向受冲击后的位移没有较大突变且冲击力能够达到额定力，则说明实验构件没有损坏，即新型耗能减震装置的抗冲击性能良好。图8～图10为加载频率保持10 Hz不变，依次增加冲击力的条件下得出的力-时间-位移(F-t-S)曲线。

(a) 上拉F-t-S曲线

(b) 下压F-t-S曲线

(a) 上拉F-t-S曲线

(b) 下压F-t-S曲线

(a) 上拉F-t-S曲线

(b) 下压F-t-S曲线

从图8～图10可看出：在各工况下的冲击力均能达到额定力且正反两方向受冲击后产生的位移均相差无几，说明该装置在两个方向上性能一样。由图10可知，当冲击力达到310 kN时，新型装置的位移只有2.115 mm，说明该装置在受到较大冲击力时位移非常小，故可以证明该新型装置的抗冲击性能良好。

3.3 抗冲击相关性

相关性实验主要用于研究该新型装置的位移与力、频率的相关性。通过保持某一参数值不变而改变另一参数值，对比分析测得的位移，从而判断新型装置工作时位移的稳定性。

图11～图15为新型装置保持加载频率不变，改变冲击力时的S-t(位移-时间)曲线。下图中0～2 s均为实验准备时间。

图11 位移与冲击力的相关性(3 Hz)

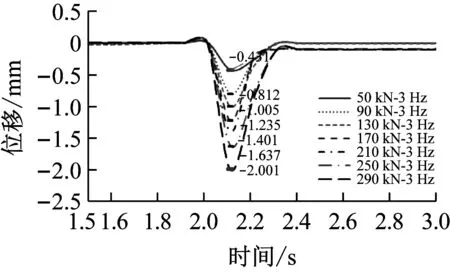
图12 位移与冲击力的相关性(5 Hz)

图13 位移的冲击力相关性(7 Hz)

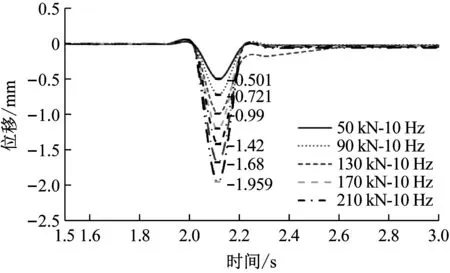
图14 位移与冲击力的相关性(10 Hz)

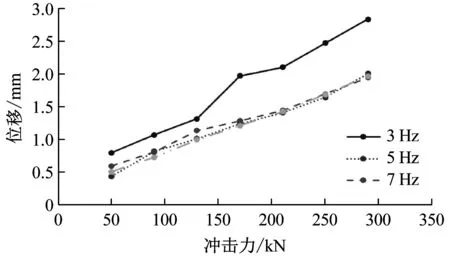
图15 位移与冲击力的关系曲线

从图11～图15可知：①在频率保持不变的情况下，新型装置的位移随冲击力的增加而增大，但位移值总体上较小。②在冲击力保持恒定不变的情况下，新型装置的位移随频率的增加逐渐趋于稳定。故可知，该新型装置在冲击力作用下，位移很小，具有很好的抗冲击性能。

4 新型装置主要力学参数的确定

借鉴国内外相关学者的研究成果[14]。本文采用Maxwell模型作为所研发的新型耗能减震装置的理论模型基础。Maxwell模型(图16)由一个阻尼单元(C0)和一个弹簧单元(K)构成，弹簧单元K代表阻尼器的内部刚度。图中Fd(t)为阻尼力，u(t)为阻尼器位移。

图16 Maxwell模型示意图

Maxwell 模型阻尼力Fd(t)表达式为：

(4)

影响阻尼系数C的因素主要为剪切面积Ae、剪切间隙d、阻尼液动力黏度μ。影响阻尼速度指数α的主要因素为阻尼液的黏度。经过对低周反复加载实验结果的分析可知，加载速度与阻尼力之间存在一定的相关性，α可取定值。故可根据现有理论和实测值进行拟合，进一步确定α的取值。

根据之前的分析可知，每个工况的滞回曲线中均有长1 mm、阻尼力为0的传动失效部分。这种现象是由于实验设备的作动头没有抗扭能力，需要加装抗扭装置导致的。在实际工作环境中，连接件有一定的抗扭能力，不会出现这种现象。因此，需对上述实验实测值进行调整，才能反映该新型耗能减震装置在实际工作条件下的滞回特性。根据上述分析，实验实测值的有效部分,如图17所示。

图17 调整后滞回曲线对比

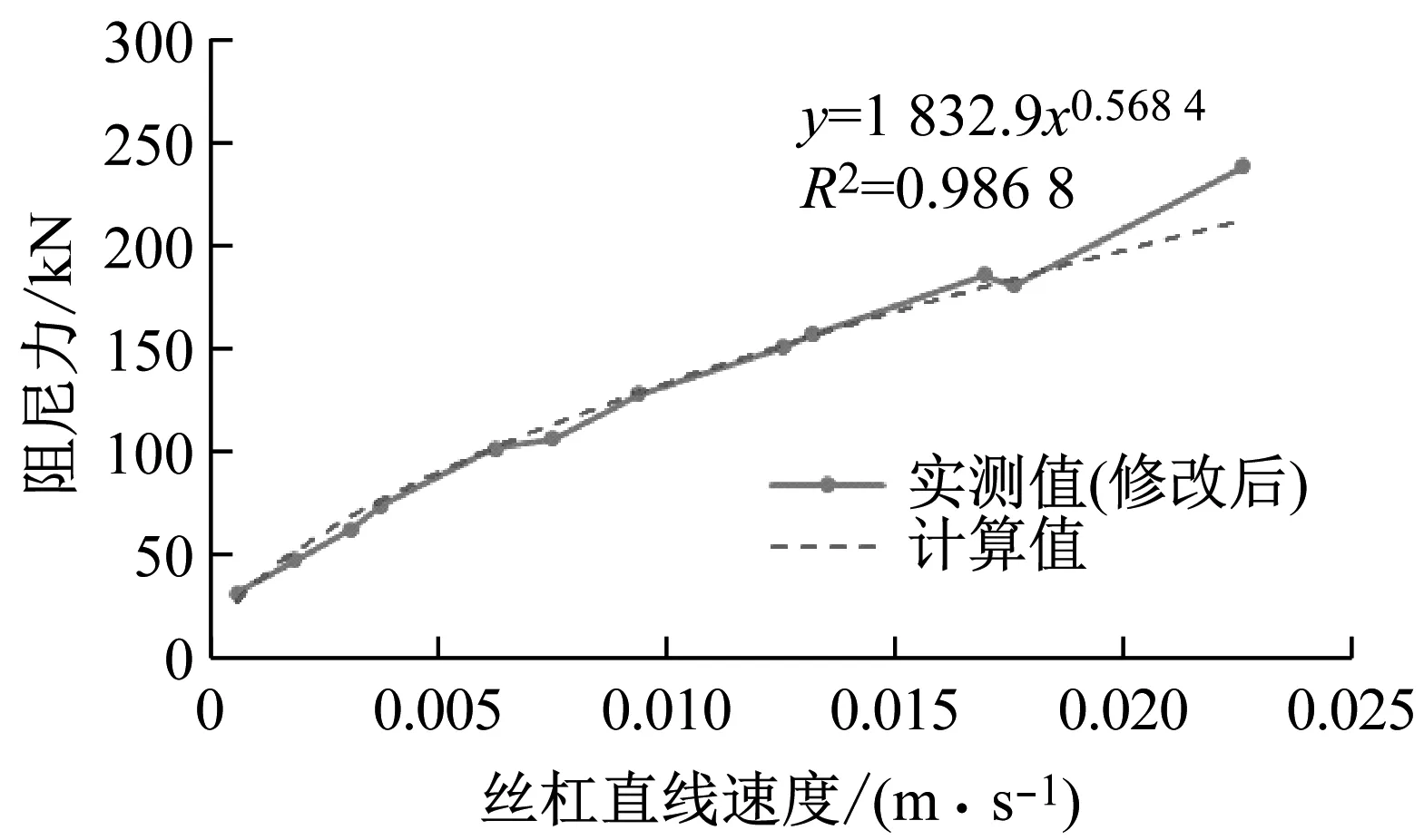
图18 阻尼力的速度相关性

图18中，虚线为根据现有理论和实验实测值拟合出的计算值，实线为修改后的实验实测值。从图18可看出，计算值可以较好的反应实测值的变化规律，其表达式为：

y=1 832.9x0.568 4

(5)

式中：y为阻尼力；x为阻尼筒旋转速度；可将α取为0.57。

借鉴以往学者对黏滞型剪切阻尼器的阻尼系数C的取值[14]，故本文取阻尼系数C=ζμtAe/d; 式中：ζ为调整系数；μt为t℃下黏滞体的黏度；Ae为剪切面积；d为阻尼筒间的剪切间隙。从上文对实验实测值的分析可知，该新型装置的刚度特性随频率的增加而越发明显，故弹性刚度对阻尼力的影响不可忽略。

在多数国内外学者对黏滞型剪切阻尼器的研究中，均忽略了弹性刚度对阻尼力的影响。而日本学者Arima等[15]提出的黏滞型剪切阻尼墙的阻尼力计算公式中同时考虑了黏滞体的黏滞阻尼力和弹性恢复力，符合本文实验结果中滞回曲线反映出的黏滞特征和刚度特性。故本文借鉴其对弹性恢复力的考虑方法对本文的实验实测值进行了拟合。且滚珠丝杠副可将直线速度转变为旋转运动，此时剪切速度可放大πR，有效提高了耗能能力。因此，综合考虑以上因素，阻尼力计算公式可表达为：

(6)

式中：F为阻尼力；μt为t℃下黏滞液体的粘度；Ae为阻尼筒的有效剪切面积；d为阻尼筒间的剪切间隙；R为可动阻尼筒的直径；L为螺杆导程；V为螺杆的直线速度；f为频率；S′为阻尼筒间相对位移。

将此计算公式与调整后的实验实测滞回曲线进行对比，以2.5 mm-0.08 Hz-3 ℃、3.5 mm-0.015 Hz-3 ℃、5.5 mm-0.02 Hz-3 ℃三个工况为例。结果如图19所示。图中计算值滞回曲线总体与实验值接近，变化趋势一致，尤其是在最值大小的预测上比较准确，再次证明了计算公式的合理性。

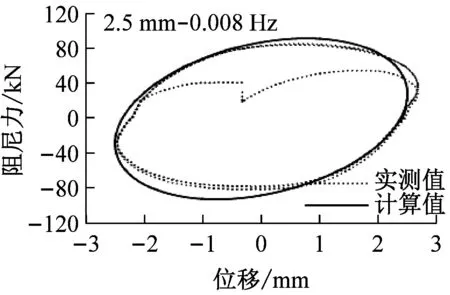
(a) 2.5 mm-0.008 Hz (b) 5.5 mm-0.02 Hz (c) 3.5 mm-0.015 Hz

5 结 论

(1) 所研发的新型装置在低速稳态输入下耗能性能较好，滞回曲线形状饱满，且多次循环加载对滞回曲线形状无明显影响，装置的耗能性能较为稳定；随加载频率的增大，装置的耗能能力逐渐增强，刚度逐渐增大，具有更强的位移限制能力。装置稳定高效的耗能能力可以满足桥梁结构在地震作用下的安全性，使结构不发生破坏。

(2) 高速瞬时输入下，频率保持不变，新型装置的位移随冲击力的增加而增大，但位移值很小；冲击力保持不变，新型装置的位移随频率的增加逐渐趋于稳定。该新型装置在冲击力作用下，位移稳定，具有很好的抗冲击性能。可保证地震发生瞬间，桥梁结构的整体刚度不发生突变，主梁和轨道不发生较大的横向变形和振动，满足高速运行的列车的行车安全性需求。

(3) 新型耗能减震装置的耗能能力与加载速度相关，在保持最大加载速度一定的情况下，不同工况下的最大阻尼力均一致。当加载速度增大时阻尼力随之增加，表明该装置属于速度型阻尼器的范畴。通过对实验实测数据的分析并结合现有理论，提出了新型装置的阻尼力公式，可为实际工程应用提供理论依据。