静钻根植竹节桩竖向动力响应研究

王奎华， 肖 偲， 高 柳， 吴君涛

(1. 浙江大学 滨海与城市岩土工程研究中心， 杭州 310058； 2. 浙江大学 软弱土与环境土工教育部重点实验室， 杭州 310058)

静钻根植竹节桩是从日本引进的新桩型，是一种高强预制桩，桩身呈竹节状。在施工过程中，首先利用螺旋钻机搅拌成孔，并在搅拌过程中注入预先配制的水泥浆液，与孔内泥浆均匀拌合成混合泥浆，然后通过吊车将桩放入孔内，依靠桩身自重即可完成沉桩。近年来，众多学者对静钻根植桩的静力特性进行了研究，周佳锦等[1-6]通过模型试验、现场试验和数值模拟等方法对其进行了深入研究，分析了桩身竹节、桩土接触面、桩周水泥土对桩身承载力与沉降控制的重要作用。

除了静钻根植桩的静力特性外，对其动力特性的研究也很重要。低应变反射波法是现行的一种最简单易行且有效的桩身完整性检测方法，对于静钻根植桩来说，由于其桩身和桩侧水泥土的特殊性，桩顶振动响应与普通桩有很大差异，在实际工程检测中，易引起误判、错判，一定程度上影响了这种桩型的推广使用。近年来，王奎华等[7-9]分别利用平面应变模型、桩周土竖向波动的轴对称模型研究了在径向非均质土中静钻根植竹节桩的振动特性，指出了竹节参数、桩周水泥土对桩顶复阻抗的影响，但是对时域特性的研究没有涉及。此外，随着制桩技术的提高，预制竹节桩直径也在增大，再加上竹节的存在，桩身振动时的横向尺寸效应已经不能忽略，郑长杰[10]，吴文兵[11-13]，高柳[14-15]等采用Rayleigh-Love杆模型，分别研究了大直径管桩和楔形桩的动力特性，考虑桩身的横向惯性效应，得到了很多有用的结论。另外，在施工过程中，桩周水泥土搅拌均匀性、周围土体的渗透性差异都将影响竹节桩的动力响应。

鉴于此，本文采用了平面应变模型[16-20]，虚土桩模型[21]， Rayleigh-Love杆模型[22]，分别考虑了桩周土的径向不均匀性、桩底土响应、桩身横向惯性效应。。在此基础上，对竹节半径、间距、桩身泊松比和桩周水泥土参数、渗透范围及不均匀性进行分析，研究静钻根植竹节桩的动力响应。

1 计算模型和基本假设

1.1 计算模型简图

如图1所示，静钻根植竹节桩桩长为H1，虚土桩长度为H2，虚土桩底部为基岩。A-A截面为正常桩身位置，B-B截面为竹节凸起位置，桩身内半径为rd，外半径为r1，竹节半径为d，相邻竹节间距为dl，桩周水泥土范围半径为rc。

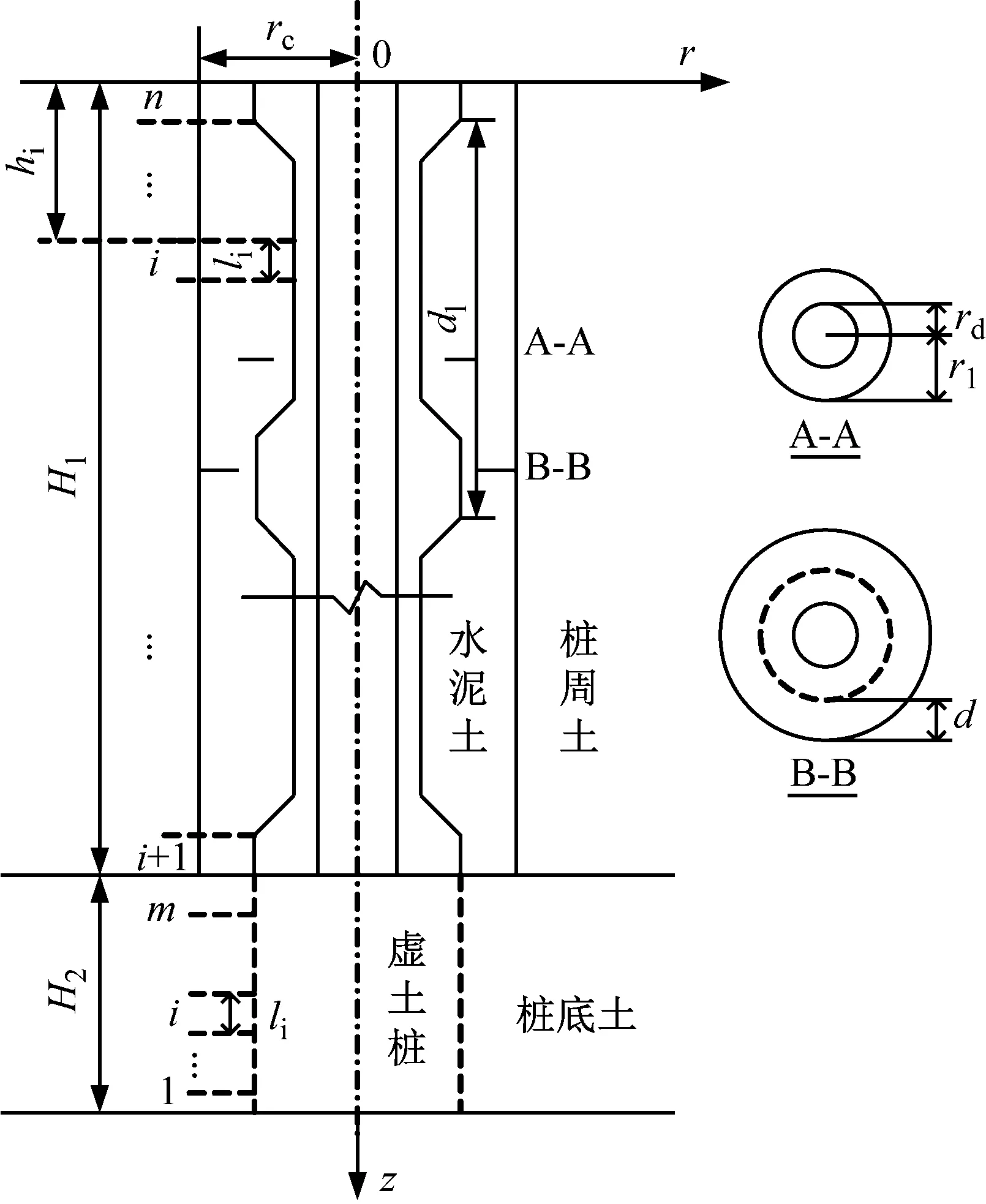
图1 静钻根植竹节桩及桩土相互作用模型示意图

采用虚土桩模型模拟桩底土对桩的支承作用，将桩底至基岩之间的土体看作虚土桩，参数取实际桩底土的参数。根据竹节特性，桩周土和桩底土的成层性，将桩土体系自下而上划分为n个微元段，如图1所示，其中虚土桩为1,2,…,m，竹节桩为m+1,…,n，竹节处采用吴文兵等楔形桩处理方法，li表示每个微元段的长度，hi表示每个微元段顶部的纵坐标，在竹节处分段数量适当增加，当微元段划分数量足够多时，可以满足计算精度要求。

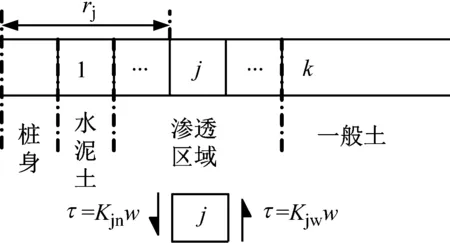
图2 桩周土几何模型

如图2所示，考虑桩周土的径向非均质特性，桩周土分为三个区域：水泥土，水泥土渗透影响区域，未受影响区域。将其沿径向划分为k圈层，各圈层内部土体径向均质，第j圈层内侧与桩轴心之间的距离为rj，其中rk=rb，r2=rc。

1.2 基本假设条件

为建立桩土体系纵向振动控制方程，本文做出以下假设：

(1) 桩(虚土桩)为黏弹性体，各桩段接触面上满足力的平衡和位移连续条件；

(2) 桩周土采用平面应变模型，桩周土层沿径向无限延伸，土体表面为自由界面，土层底部为刚性支承边界；

(3) 桩与桩周土完全连续接触，桩土接触面上，土体动应力通过剪切复刚度传递给桩；

(4) 桩土耦合振动为小变形振动；

(5) 桩周土为单相土，不考虑地下水的影响。

2 方程的建立和求解

2.1 桩周土层振动方程及求解

根据Novak等[17]提出的平面应变模型可知，桩体的纵向振动所引起的桩周土体的径向位移可以忽略，主要考虑竖向位移，设wj=wj(r,t)为任意竖向层第j圈层土体的竖向位移，其位移控制方程为：

(1)

式中:

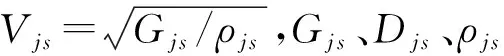
式(1)的解可以表示为：

wj(r)=AjK0(ξjr)+BjI0(ξjr)

(2)

式中:K0(ξjr)和I0(ξjr)分别为第一类和第二类零阶虚宗量贝塞尔函数；Aj和Bj为待定常数，可以根据边界条件得到。

第j圈层土体中的竖向剪切应力可以表示为：

(3)

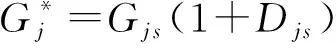
对于外圈未影响区域:

在这个区域中,j=k。根据土体径向无穷远处竖向位移为零，可以得到Ak=0。根据剪切刚度的定义，可以得到未影响区域内侧和渗透影响区域外侧接触面的剪切刚度如下：

(4)

对于水泥土区及其渗透区域:

在这个区域内, 1≤j≤k-1。同样地，第j圈层的外侧剪切刚度可以表示为：

(5)

其中，

由此，可以得到

(6)

相似地, 由于相邻圈层接触面两侧剪切刚度互等，第j圈层的内侧剪切刚度和第j-1圈层的外层剪切刚度可以表示为:

(7)

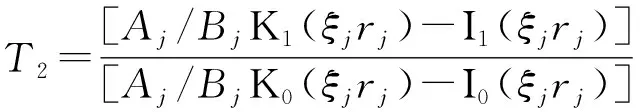
根据式(5)～(7)，可以得到任意圈层的外侧和内侧的剪切刚度递推关系，再结合式(4)，逐层递推，可以得到任意桩段桩身外侧与水泥土接触面的剪切刚度。

2.2 微元段桩振动方程及求解

虚土桩段振动方程：

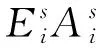
i=1,2,…,m

(8)

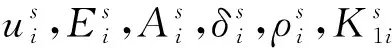
静钻根植竹节桩段振动方程：

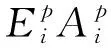
(9)

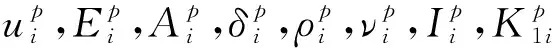
桩土耦合振动过程中应满足边界条件、初始条件和位移及截面力连续条件：

(1) 边界条件

虚土桩桩底：

(10)

静钻根植竹节桩桩顶：

(11)

(2) 初始条件：

位移：

ui|t=0=0

(12)

速度：

(13)

(3) 位移和截面力连续条件：

虚土桩(i=1,2,…，m)：

(14)

(15)

静钻根植竹节桩(i=m+1,m+2,…，n)：

(16)

(17)

结合初始条件式(12)、(13)，对虚土桩和静钻根植桩振动方程进行拉普拉斯变换，可得：

虚土桩：

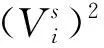
i=1,2,…，m

(18)

静钻根植桩：

(19)

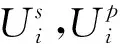
方程式(18)，(19)解的统一形式为

(20)

对于虚土桩：

(21)

对于静钻根植竹节桩：

i=m+1,m+2,…,n

(22)

式中：ti为应力波在第i段桩身(虚土桩)传递的时间。

根据位移阻抗函数定义(力除以位移)，结合连续条件，可得第i段微元段顶部截面处的位移阻抗函数的解析表达式：

对于虚土桩(i=1,2,…，m)：

(23)

其中

对于静钻根植竹节桩(i=m+1,m+2,…，n)：

(24)

其中

且由竹节桩与虚土桩的连续条件，有

(25)

式中：Ap和As分别为竹节桩桩底和虚土桩的横截面积。

通过阻抗函数递推公式，可以得到静钻根植桩桩顶复阻抗，将桩顶复阻抗表示成复数表达式如下：

(26)

静钻根植竹节桩桩顶速度幅频响应函数表达式为：

(27)

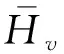
(28)

在进行低应变动态测试时，常使用尼龙锤敲击桩顶，对其施加一个激振力，该激振力近似为半正弦曲线。为了贴近实际，假设桩顶受到半正弦激振力为：

(29)

式中:T0为激振力脉冲持续时间;q0为激振力峰值。

对激振力进行傅里叶变换，可得：

(30)

再对Q(ω)Hv(iω)进行傅里叶逆变换得到桩顶速度时域响应函数半解析解：

(31)

(32)

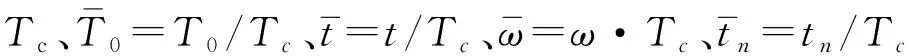
3 本文解的合理性验证

接下来对本文解的合理性进行简单的验证，理论上来说，本文的解可以适用于桩周土纵向任意分层的情况，只需将对应参数取实际值即可。静钻根植竹节桩实际上是一种特殊的管桩，由于其桩身结构特殊，桩周水泥土施工影响大，造成其桩身动力特性与其他桩型有较大差异。现在对本文中计算模型进行退化，与其他已有模型进行对比，以验证本文解的合理性。

在以下分析过程中，桩土系统参数若无特别说明，取值如下：桩底土和桩周未受影响土的剪切波速和密度分别为150 m/s和1 800 kg/m3，桩周水泥土剪切波速和密度分别为300 m/s和2 000 kg/m3，水泥土区域半径为0.8 m，其中水泥土渗透区域的剪切波速由水泥土波速到未受影响土波速线性变化。虚土桩半径为0.5 m，纵波波速为500 m/s，阻尼系数为0.001。静钻根植竹节桩相关参数，如表1所示。

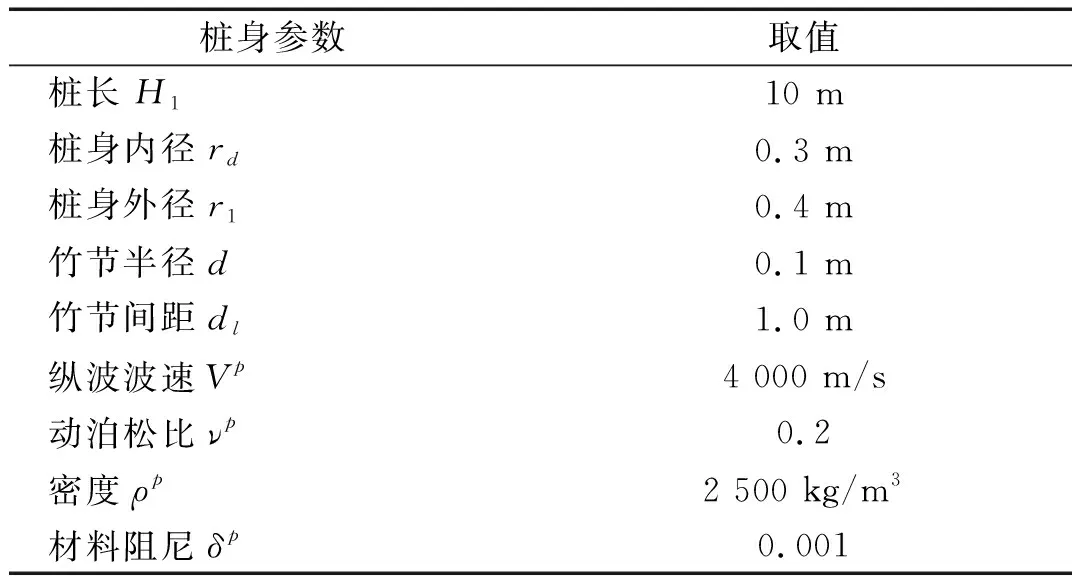
表1 静钻根植竹节桩参数

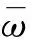
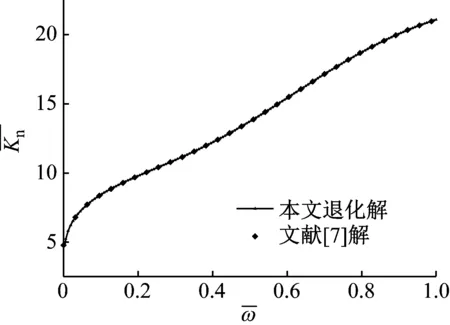
(a) 动刚度

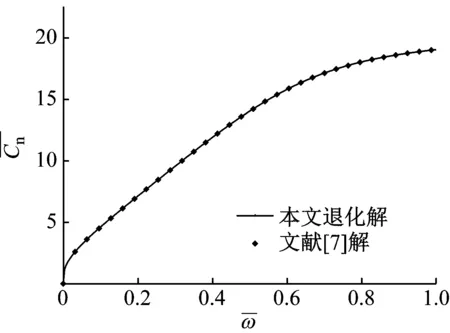
(b) 动阻尼

为了进一步验证本文解的合理性和实用性，本文选取了宁波某管桩场地内的静钻根植竹节试桩进行低应变测试，测试结果与理论曲线进行对比。

该试桩采用静钻根植工法成桩，桩长为12 m，桩身外径0.25 m，桩身内径0.15 m，竹节厚度0.1 m，竹节间距1 m。根据地勘资料，桩周土剪切波速约为180 m/s，桩底软土层厚度约为7 m。桩周水泥土龄期为7天，室内实验测得水泥土剪切波速为210 m/s，低应变测试时锤击时长为0.7 ms。实测曲线与理论曲线对比如图4所示，可以看到，两条曲线变化规律基本一致，但是还存在一些差异，这是因为室内试验中水泥土试块的养护、均匀性等条件不同，导致测得的水泥土剪切波速不一致，另外理论计算和实测时激振条件的差异也会引起曲线不一致。

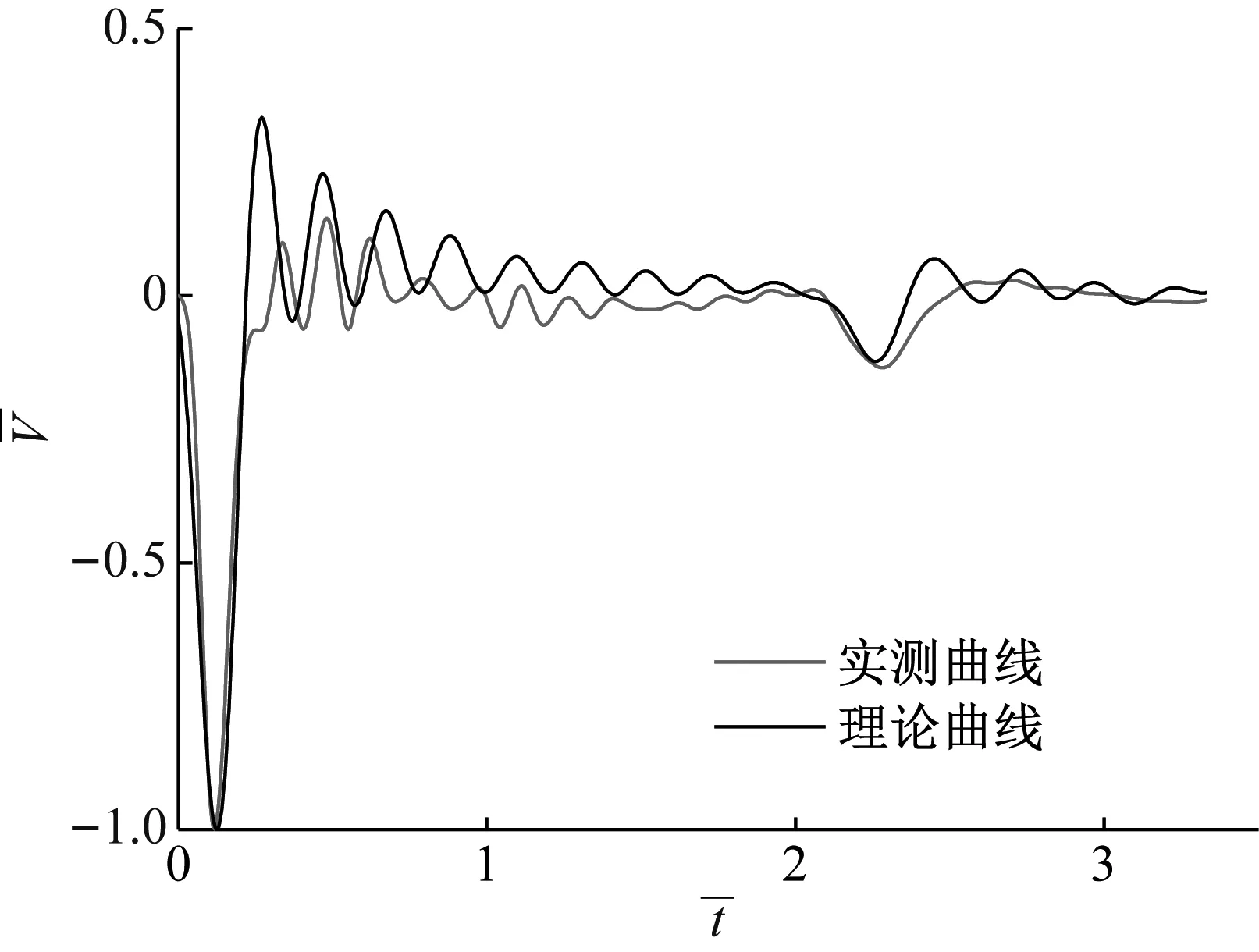
图4 本文解与实测曲线对比

4 参数分析

接下来对静钻根植竹节桩桩顶动力响应进行参数分析，主要研究竹节半径、竹节间距、桩身泊松比、桩周水泥土剪切波速、水泥土不均匀性以及水泥土渗透影响范围对低应变测试中桩顶响应的影响。

4.1 竹节半径对桩顶响应的影响

静钻根植竹节桩的特殊之处就在于桩身周围存在类似于竹节的凸起，竹节尺寸通过竹节半径d反映，其中d=0 m表示桩身无竹节。

如图5所示为竹节半径对桩顶动力响应的影响。由图5(a)可知，随着竹节变大，桩顶速度导纳振荡峰值减小，共振周期变小，且随着频率的增大，共振周期减小幅度进一步增大。由图5(b)可知，随着竹节尺寸增大，桩身在各竹节处的反射逐渐增强。而桩底反射信号出现了延迟现象，且竹节尺寸越大，延迟越明显。这是因为考虑了桩身振动的横向惯性效应，竹节尺寸越大，横向惯性效应越明显，由此导致的反射信号延迟也相应增加。

4.2 竹节间距对桩顶响应的影响

如图(6)所示为竹节间距对桩顶响应的影响。由图6(a)可知，在低频时，不同竹节间距的导纳曲线基本一致，随着频率的增加，竹节间距越大，共振峰值越大，但振动周期基本一致，当频率高到一定程度时，导纳曲线出现紊乱。由图6(b)可知，随着竹节间距增大，桩身在竹节处的反射逐渐增强，但桩底反射逐渐变弱，因为在桩身竹节的反射中消耗了更多能量。另外，竹节间距越小，竹节分布越密集时，桩身时域响应越接近于均匀等截面桩。

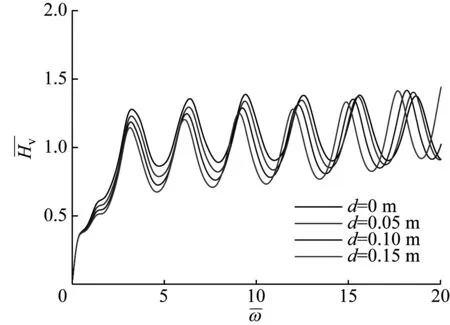
(a) 频域响应曲线

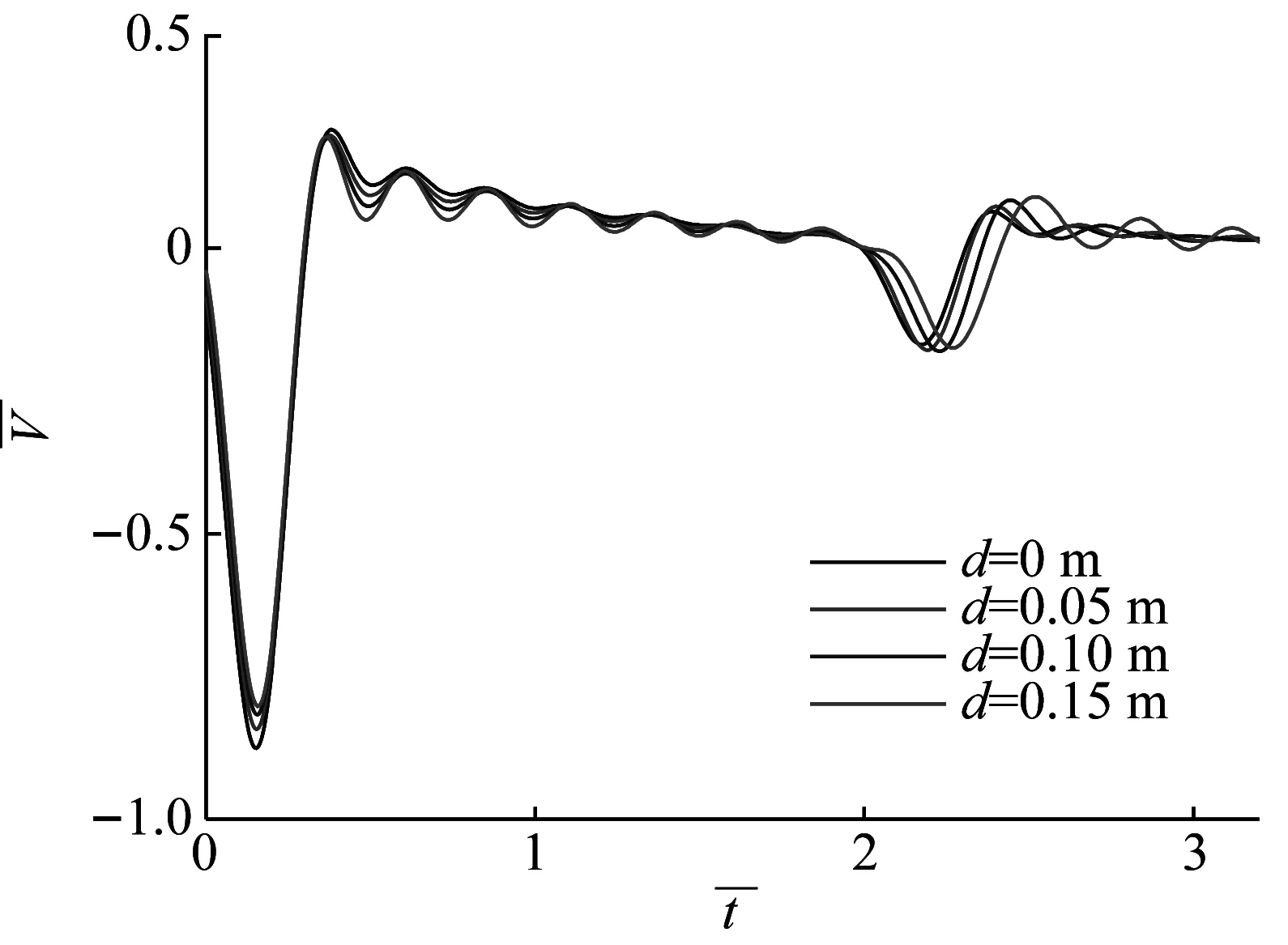
(b) 时域响应曲线

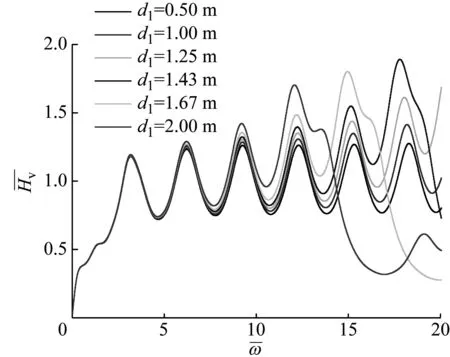
(a) 频域响应曲线

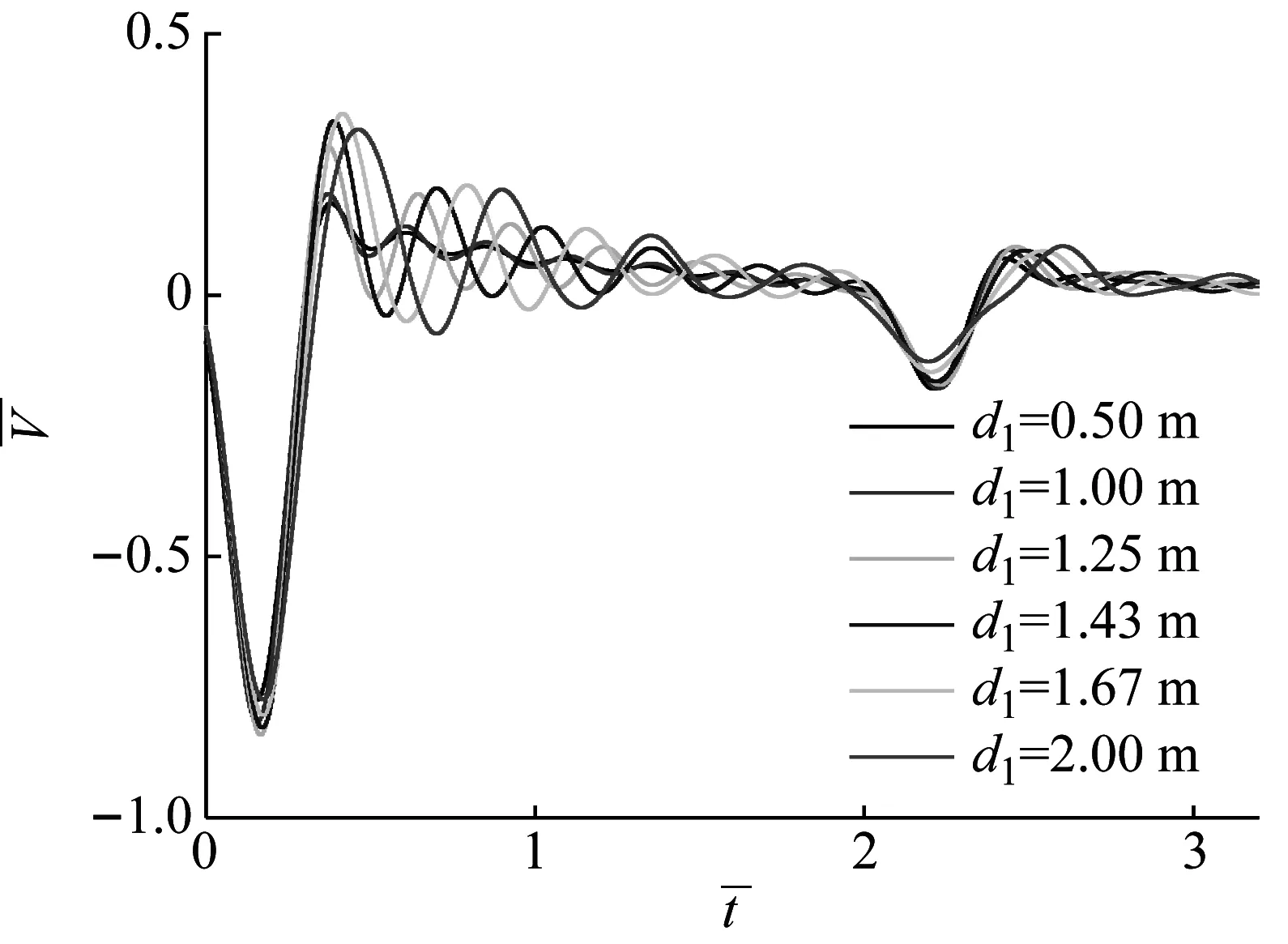
(b) 时域响应曲线

4.3 桩身泊松比对桩顶响应的影响

如图7(a)所示为桩身泊松比对桩顶动力响应的影响。由图7(a)可知，泊松比和竹节尺寸变大时，桩顶共振峰值减小，共振周期减小，且随着频率的增大，这种差异更加明显，值得注意的是泊松比变化对其的影响明显大于竹节尺寸变化的影响。由图7(b)可知，泊松比和竹节尺寸的变大都会导致桩底反射峰值减小和时间延迟，而且竹节尺寸越大，泊松比变化对其影响就越明显，尤其是桩身竹节处的反射。

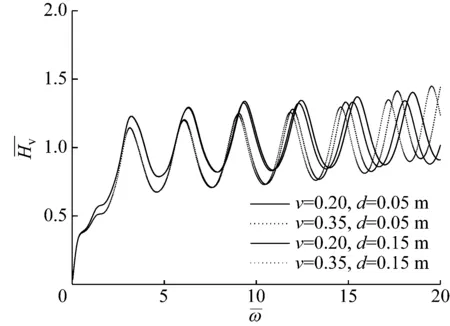
(a) 频域响应曲线

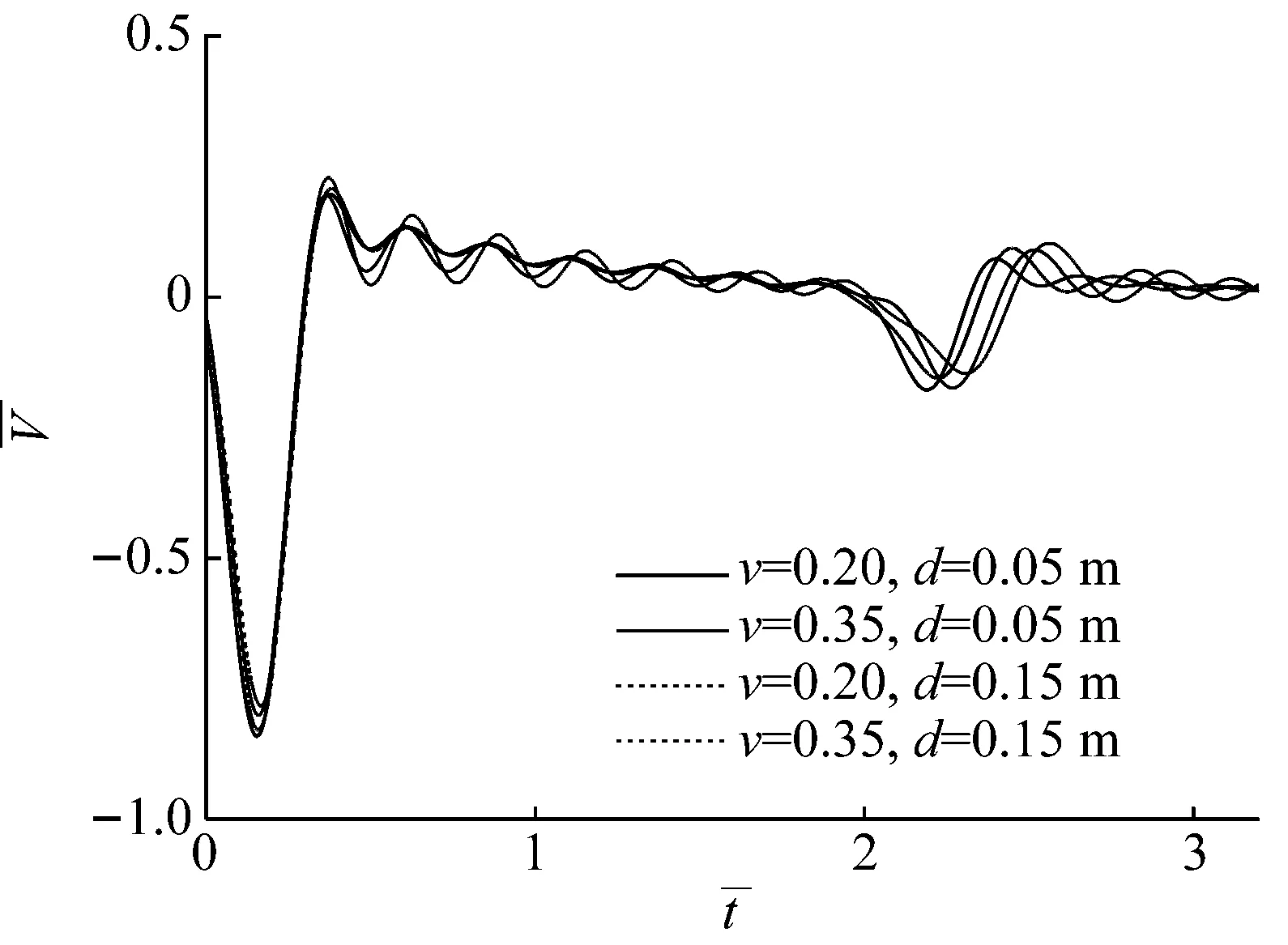
(b) 时域响应曲线

4.4 桩周水泥土波速对桩顶响应的影响

桩周水泥土在施工后随着龄期逐渐硬化，但是目前并没有相关的试验测试桩周水泥土剪切波速变化规律。根据周佳锦[22]所做的水泥土强度和压缩性试验，可以估算桩周土水泥土28天剪切波速在500 m/s以下。图8所示为桩周水泥土剪切波速对桩顶响应的影响。

由图8(a)可知，随着水泥土剪切波速的提高，共振峰值逐渐减小，但是不会影响共振频率。由图8(b)可知，随着水泥土剪切波速提高，桩底反射信号逐渐减弱，当剪切波速达到一定值时，桩底和桩身竹节的反射变得很微弱。这就说明在低应变检测桩身质量时有一个临界时间，在这个时间之后，水泥土达到一定强度，桩底反射信号就难以获取，不利于桩底反射信号的获取和缺陷的判断。具体时间的确定还需对桩身水泥土剪切波速时效性进行试验探究，同时也和桩土相关参数有很大关系，有待进一步研究。

(a) 频域响应曲线

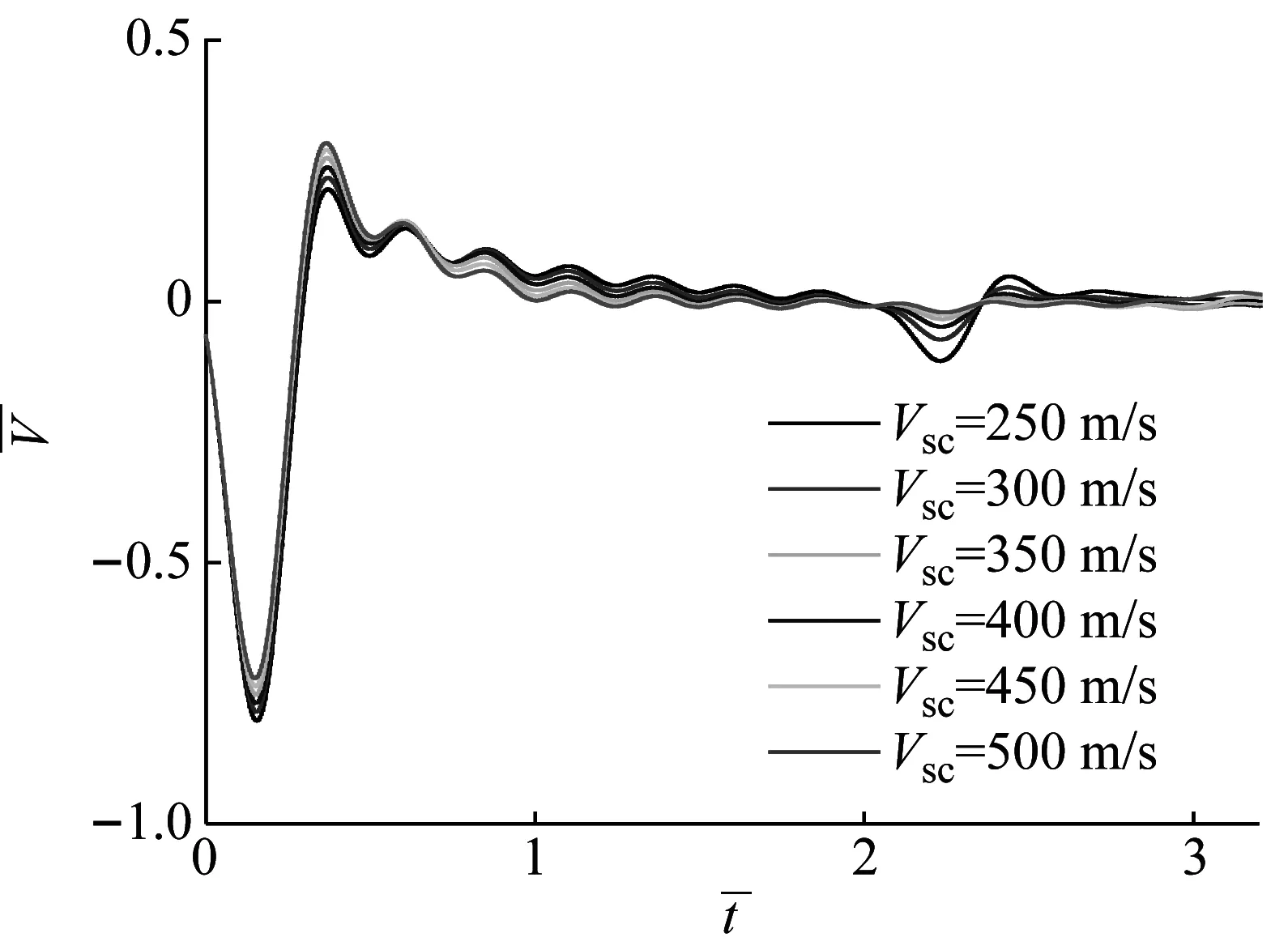
(b) 时域响应曲线

4.5 桩周水泥土不均匀性对桩顶响应的影响

在静钻根植竹节桩现场施工时，桩周水泥土的施工质量非常重要，很容易出现水泥土搅拌不均匀的工况。图9所示为桩周水泥土不均匀性对桩顶动力响应的影响。在桩身水泥土区域设置厚度为20 cm的环形不均匀层，不均匀层中水泥土剪切波速为均匀层水泥土剪切波速的1.5倍，图中hd表示不均匀层位置与桩顶的距离，hd=0 m表示没有设置不均匀层。

由图9(a)可知，在低频和高频段，水泥土的不均匀性对导纳影响不大，但是在中间频段，出现了共振峰值和频率的变化。由图9(b)可以看到，桩顶时域曲线在不均匀土层处出现了较为明显的异常反射，与不设置不均匀层的曲线对比来看，设置不均匀层时，曲线在对应位置处产生了与入射波相反方向的反射信号，与桩身扩颈相似，而紧接着又会产生与入射信号相同的反射信号，与桩身缩颈相似，而且桩底反射也有一程度的减弱，这在低应变检测时应引起注意，容易与桩身缺陷处反射混淆。

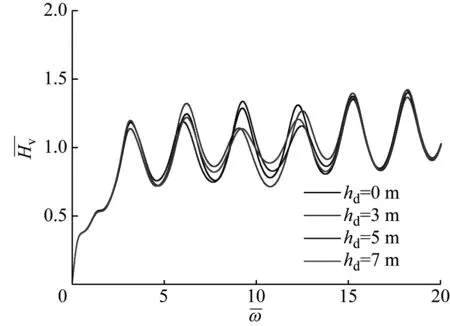
(a) 频域响应曲线

(b) 时域响应曲线

4.6 水泥土影响范围对桩顶响应的影响

图10所示为桩身水泥土渗透影响范围对桩顶动力响应的影响。令影响区域外侧半径为rb，水泥土区域外侧半径为rc，θ=rc/rb表征水泥土影响范围。

由图10可以看出，在桩身水泥土基本参数不变时，水泥土渗透影响周围土体的范围大小对桩顶动力响应影响不大，几乎可以忽略。

5 结 论

采用平面应变径向非均质土模型模拟桩侧土、虚土桩模型模拟桩底土，考虑了桩身竹节的横向惯性效应，求得了桩顶频域响应解析解和时域响应的半解析解，通过参数分析的方法研究了桩土参数对桩顶动力响应的影响，结论如下：

(1) 竹节的存在会导致时域曲线中桩身出现多次反射信号，桩底反射信号因为横向惯性效应产生的时间延迟会随竹节尺寸增大而变得更加明显，而且桩身泊松比增大也会放大这一效应。因此，在进行低应变测试理论分析时，竹节桩的横向惯性效应不可忽略。

(a) 频域响应曲线

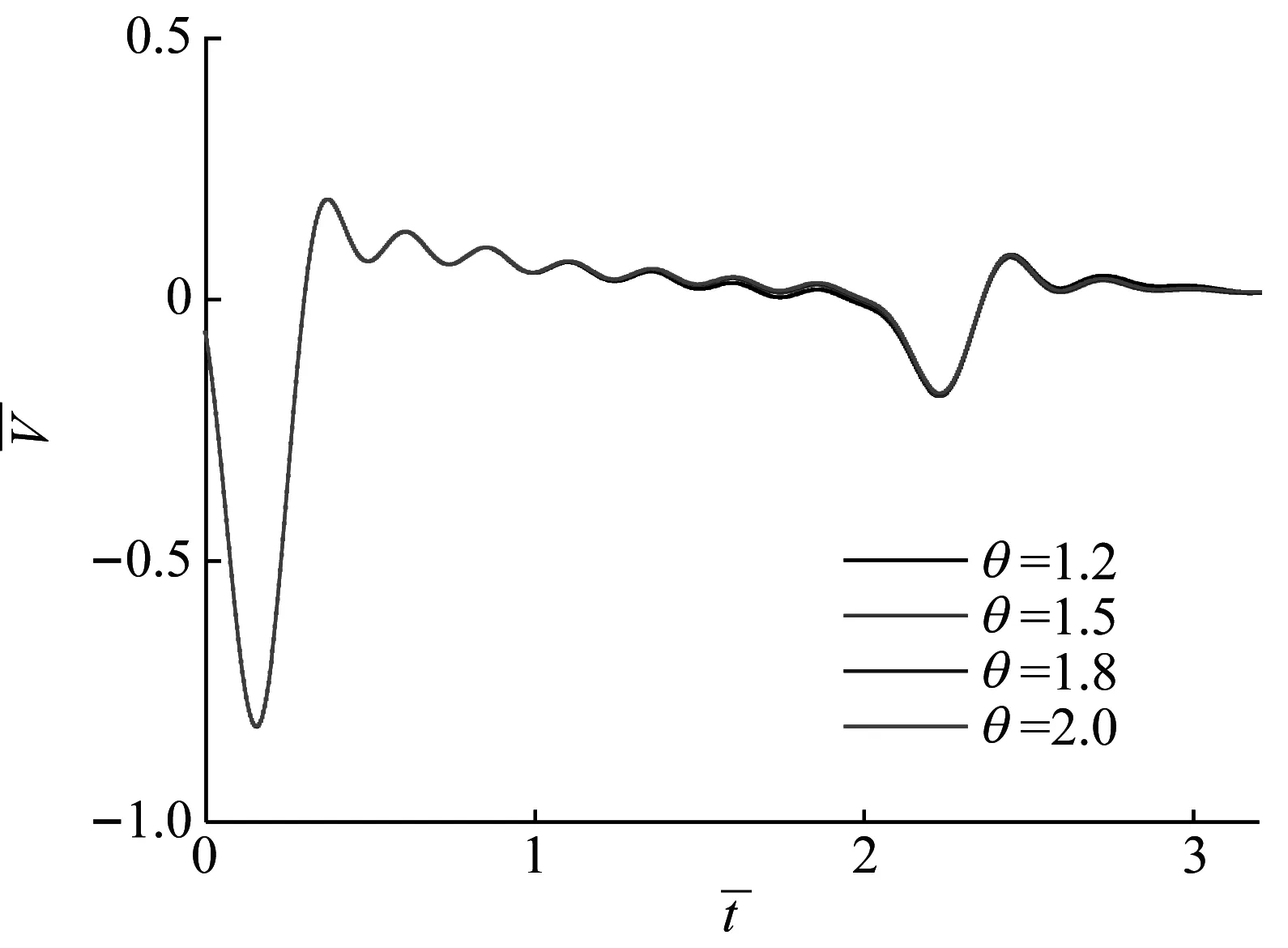
(b) 时域响应曲线

(2) 竹节间距较大、水泥土局部不均匀、竹节尺寸较大都会导致桩身出现较大反射，在桩身低应变完整性检测中应该引起注意，避免误判。

(3) 水泥土渗透范围对桩顶动力响应影响不大，而随着桩周水泥土龄期增长，水泥土剪切波速逐渐增大，振动时桩侧能量耗散增大，导致竹节桩反射信号变得很微弱，因此在低应变检测时应该确定合理的检测时间。此外，水泥土剪切波速随着龄期变化规律需进行进一步试验研究。