平面P波入射半无限介质内运动空间特征研究

何卫平, 周宜红

(1.三峡大学 湖北省水电工程施工与管理重点实验室，湖北 宜昌 443002;2.三峡大学 水利与环境学院，湖北 宜昌 443002)

受到地质地形条件影响，地震波在场址引起的地震动具有空间差异性[1]。研究显示，地震动的空间差异不仅影响结构地震响应规律，也可能带来结构地震响应的显著增加[2-5]。桥梁、核电站和大坝等大跨度结构的地震安全性评价体系中，获得能合理描述地震动空间差异的输入模型是亟待解决的问题。

已有研究显示，引起地震动空间差异的原因主要有行波效应、衰减效应、相干效应和局部场地效应等因素。目前工程应用领域通常采用相干函数模型描述地震动的空间差异[6]，已有相干函数模型主要可区分为通过实测台阵记录总结得到的经验模型[7-8]，和结合实测台阵记录与理论分析的半经验模型[9-10]。相干函数为描述地震动空间相关性提供了合理的途径，已提出的诸多相干函数模型可为工程结构的非一致地震响应分析提供应用基础。然而，大坝、核电站的地震响应分析通常不仅关注地面运动，还关注地基内一定深度的地震动[11-12]。另外，相干函数属唯象模型，侧重地震动空间差异的经验性描述，没有从物理过程考察地震动场的特征[13]，在解释地震动空间差异的形成机理方面略显不足。现阶段，研究地震动空间差异的形成机理，是解决空间差异地震动输入模型的关键环节。

空间差异地震动是入射地震波在场址条件下形成的运动，从形成机理出发研究地震动场，必须从入射波形成场址运动场出发。在地震波引起的空间运动研究方面，目前在波动输入模型方面有所涉及。如刘晶波等[14-15]在发展黏弹性边界波动输入模型时对侧边界运动的处理，考虑了入射波与反射波的叠加影响。但波动输入模型侧重于输入相关运动，在解释地震动空间差异方面关注较少。另外，在工程应用领域，以描述地震动空间差异为目标的模型有金星等[16]提出的地震动随机场模型和张翠然等[17]提出的随机有限断层法模型。这两类模型均以随机方法为基础，通过模拟地震波从震源到场址的传播过程构建地震动场。

本文尝试从波动理论及叠加原理出发研究场址小范围内的确定性地震动空间差异，讨论范围除地面质点运动外，也包含地基内质点的运动。文中首先以半无限介质内入射P波与SV波叠加形成的质点运动为例，对地震波叠加模式与质点运动空间差异进行说明。然后以P波垂直入射为例，对叠加区和分离区、分界线等概念进行界定，并对由地震波叠加模式不同引起的运动空间差异进行说明。最后针对平面P波倾斜入射情况研究空间域划分，并通过算例研究叠加区内质点运动的空间特征。

1 地震波叠加模式与质点运动空间差异

地震波在介质内的传播引起质点运动，如平面P波引起的质点运动与传播方向平行，平面S波引起的质点运动与传播方向垂直。当多条地震波在相同空间区域传播时，质点运动由地震波运动叠加形成。由于空间域内的地震波可能存在波型、持时、传播方向、初至时间等的差异，不同空间位置质点的运动叠加方式存在差异。

以图1波在无限均匀介质中的传播为例，假设无限介质内存在平面P波和SV波，两条地震波持时均为2 s，位移峰值1 cm，入射角分别为40°和35°，波形如图所示，两条地震波到达A点的时间相同。依据叠加原理，可由P波与SV波的波函数获得空间内任意质点的运动时程。以地震波传播到达A点为零时刻，在图中显示了A、B、C三个空间点的水平向运动时程。

分析地震波传播特点和质点运动时程，图示A、B、C三个位置的地震波叠加模式存在如下差异。在A点，P波与SV波在相同时刻到达、相同时刻离开，A点运动的整个时段均由两条地震波叠加形成。在B点，P波先于SV波到达且更早离开，运动的前段由P波形成、中段由P波和SV波叠加形成，后段由SV波形成。在C点，P波首先到达并通过，此后SV波到达并通过，质点运动前段由P波形成，后段由SV波形成。地震波叠加模式的差异带来质点运动的差异，下面以质点运动的水平分量为例，分别从持时、峰值和时程形状三方面分析。

图1 地震波叠加模式与质点运动空间特征示意图

Fig.1 Superposition mode of waves and spatial variation of particle motion

在持时方面，A点运动整个时段均由P波和SV波叠加形成，持时为2.00 s；B点存在P波和SV波单独形成时段和叠加形成时段，持时为2.65 s；C点运动不存在两条地震波的叠加形成时段，持时为4.00 s。

在运动峰值方面，A点运动由两条地震波直接叠加形成，峰值为1.46 cm；B点运动存在两条地震波叠加贡献时段，负峰值与正峰值存在叠加影响，峰值为0.75 cm；C点运动中两条地震波的贡献时段在时域分离，峰值为0.82 cm。

在质点运动时程形状方面，从图1可知由于地震波叠加模式差异质点的运动形状存在明显的不同。

综上，介质内部地震波的传播效应和叠加模式差异会引起质点运动的空间差异，研究组合地震波对质点运动空间差异的影响，对地震动空间差异的形成机理研究具有重要意义。

2 P波垂直入射空间域划分

为对问题有较清晰的认识，首先选取较为简单的平面P波垂直入射工况，研究在入射波和反射波影响下质点运动叠加模式差异和空间域划分情况。

2.1 平面P波垂直入射

图2显示半无限均匀介质内平面P波垂直入射情况，图中空心箭头代表地震波传播方向，实箭头代表质点振动正方向。依据自由面处应力和位移边界条件，可得反射P波的幅值系数APR=-1。P波垂直入射时，半无限空间内存在入射P波(简写为PI)和反射P波(简写为PR)两条地震波，空间内质点运动是两条地震波运动的叠加。

2.2 空间域划分

以图2中质点A(x,z)为研究对象，质点运动由入射P波和反射P波运动叠加形成。由于入射波和反射波均具有固定持时，且地震波在介质中传播需要时间，两条地震波的叠加模式随A点位置而变化。

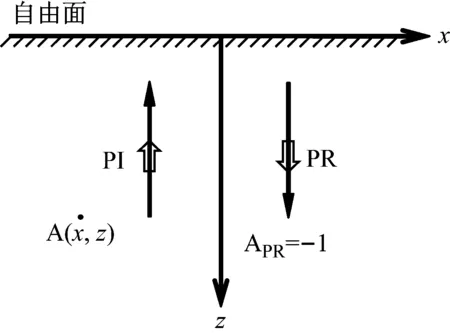
图2 平面P波垂直入射示意

A点位于自由面时，由于入射波到达自由面时立即产生反射波，两条地震波在质点运动的整个时段均有贡献，即质点运动是由两条地震波全时域叠加形成。

A点与自由面距离为z时，入射波首先到达，此后经过距离z传播到自由面并形成反射波，反射波经过距离z传播到质点。此时可依据质点位置将叠加模式分为两种情况：当质点距离自由面较近时，入射波与反射波在质点的运动时程中存在叠加贡献时段，将此类质点所在空间定义为叠加区；当质点距离自由面较远时，入射波与反射波对质点运动时程的贡献时段是分离的，将此类质点所在空间定义为分离区。自由面属于叠加区。

由于P波垂直入射，因此叠加区与分离区的分界线应为与x轴平行的直线。在图3中显示了叠加区与分离区的示意图，图中质点运动为依据第3节算例获得的区域内特征点竖直向运动时程。

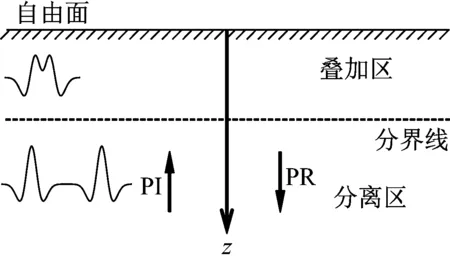
图3 质点运动叠加模式与空间区域

2.3 叠加区与分离区的分界线

以PIs和PIe分别代表入射P波到达和离开质点的时间，以PRs和PRe分别代表反射P波到达和离开质点的时间，T代表地震波持时。

以入射波到达自由面为时间零点，依据地震波速得到P波垂直入射时，入射波到达和离开空间点(x,z)的时间PIs和PIe分别表达为式(1)和式(2)，反射波到达和离开空间点(x,z)的时间PRs和PRe分别表达为式(3)和式(4)。式中z代表空间点的竖直坐标，vp代表P波传播速度，波速表达式见式(8)。

PIs=-z/vp

(1)

PIe=-z/vp+T

(2)

PRs=z/vp

(3)

PRe=z/vp+T

(4)

当入射波离开时刻与反射波到达时刻相同，即PIe=PRs时质点运动时程中两条波的贡献时段在时域相接，该质点也位于分界线上。依据式(2)和(3)得到式(5)，该式代表P波垂直入射时叠加区与分离区的分界线。

zd=vpT/2

(5)

3 叠加区域运动空间差异

3.1 介质参数及入射地震波

选取弹性模量为10 GPa、泊松比0.2、密度2 400 kg/m3的半无限弹性介质为例进行研究。为表达清晰，选取入射地震波为Ricker子波，子波运动时程在图4显示，图中位移正值代表与z轴正方向一致。

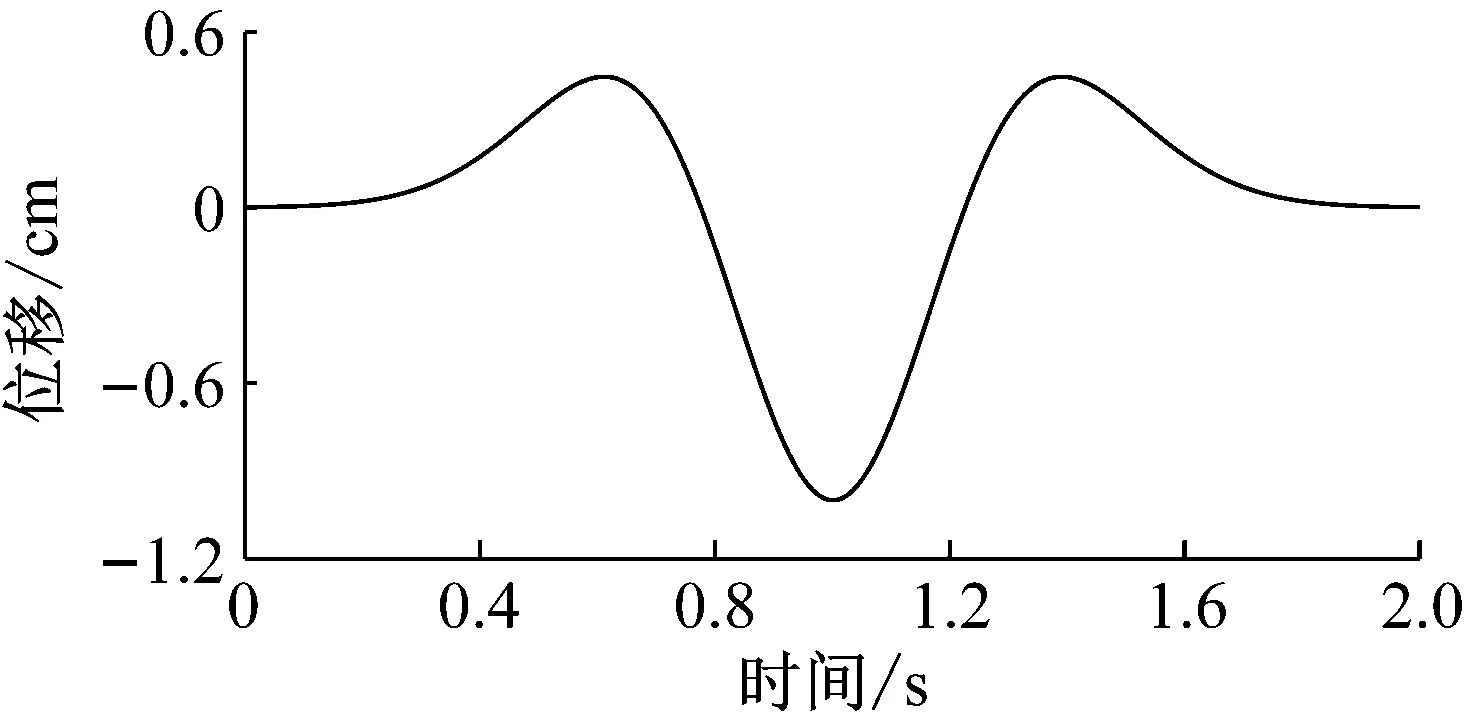
图4 Ricker子波位移时程

3.2 叠加区质点运动空间差异

P波垂直入射时，入射波与反射波引起的运动与传播方向平行，即质点运动表现为竖直向运动，因此本部分仅考察质点运动的竖向分量。依据入射波与反射波各自的波函数叠加，得到空间内任意点的运动时程。

依据介质参数和地震波持时，由式(5)得到分界线的深度为2.15 km。选取自由面和深度0.6 km的叠加区特征点研究。图5显示了两个特征点的运动时程，图中时间零点代表地震波到达该位置的时刻，斜体字及双箭头代表对质点运动时程产生贡献的地震波及其贡献时段。

在自由面上，入射波到达即产生反射波，入射波与反射波叠加形成质点运动。自由面质点运动持时与入射波持时相同，且质点运动峰值是入射波峰值的2倍。

在深度为0.6 km处，由于入射P波到达0.56 s之后反射P波到达，因此入射P波贡献时段为0～2 s；反射P波贡献时段为0.56～2.56 s。在0～0.56 s质点运动仅受入射P波影响，在0.56～2 s质点运动同时受到入射P波与反射P波影响，在2～2.56 s质点运动仅受反射P波影响。由于地震波传播效应，0.6 km深度的质点运动持时增加了0.56 s；由于入射波和反射波的叠加影响，质点运动峰值由1.00 cm减小到0.78 cm。

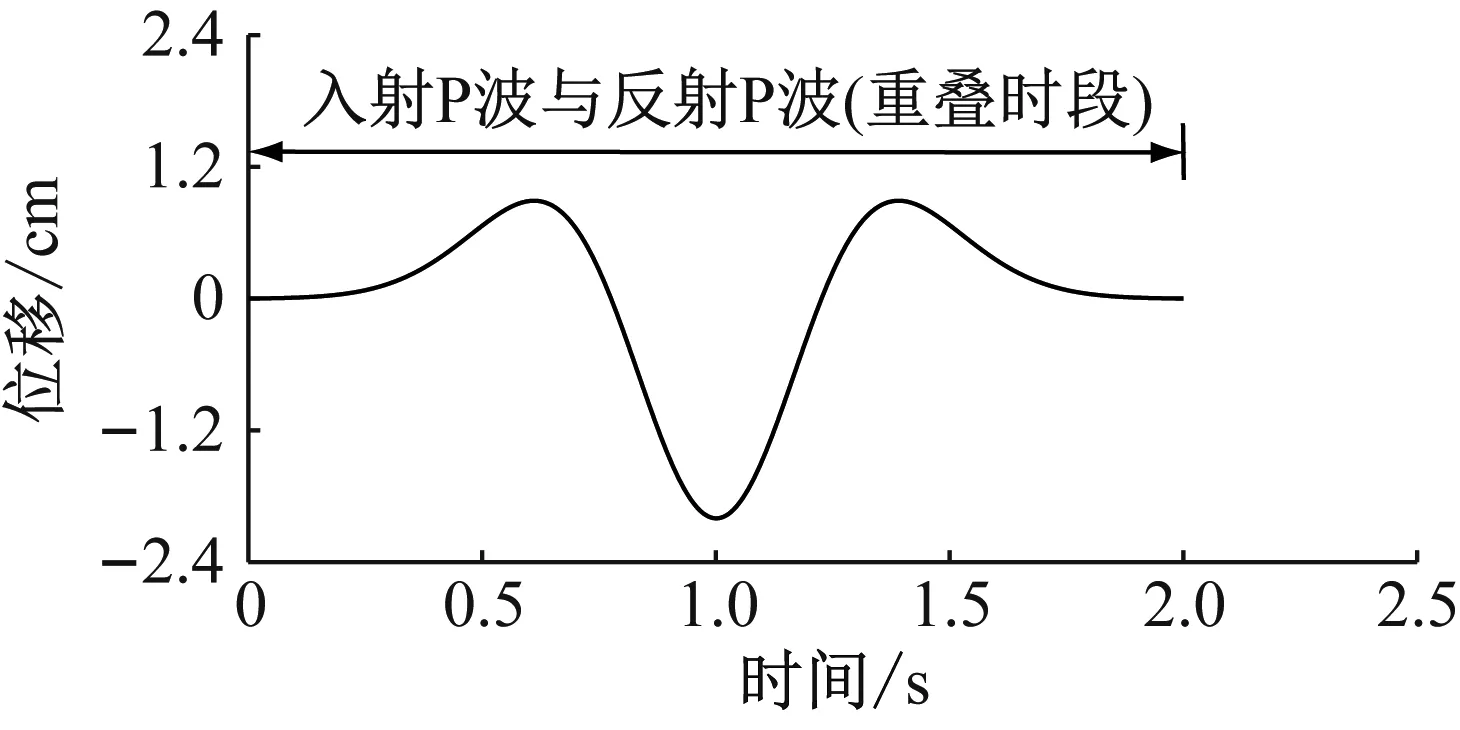
(a) 自由面

(b) 深度0.6 km

两个质点运动对比可看出：由于所处位置不同，受到地震波传播所带来的叠加方式影响，不同质点运动时程在持时、峰值和时程形状等方面均表现出较大空间差异。

图6显示了P波垂直入射时叠加区内质点运动位移峰值沿竖向分布。由于Ricker子波负峰值为单峰，对负峰值进行分析。位移负峰值主要显示出以下规律：① 叠加区峰值出现较大变幅，从地表到约0.5 km深度，位移峰值从2 cm逐渐减小到0.55 cm；② 位移峰值在一定深度以下变化到与入射波位移峰值相等。位移正峰值在接近自由面呈现出与负峰值相同的规律，但由于选用的波形存在两个正峰值，其叠加规律更为复杂，幅值变化的范围也有明显增大。

(a) 正峰值

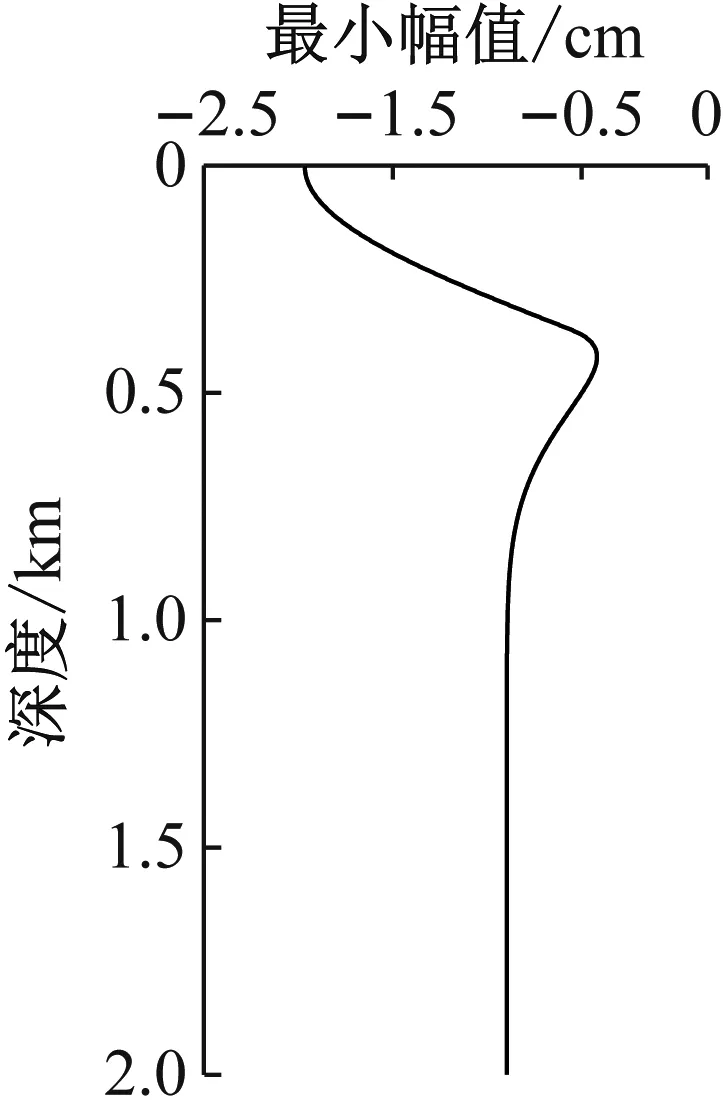
(b) 负峰值

4 P波倾斜入射质点运动空间特征

4.1 倾斜入射反射系数

P波(记为PI)倾斜入射到自由面时，会产生反射P波和SV波(分别记为PR、SR)，如图7所示。图中符号含义与前文相同，θ为P波入射角，θ′为SV波反射角。反射P波、反射SV波幅值系数分别用Ap表示。依据自由面应力和位移边界条件，可得出反射P波和SV波的幅值系数为式(6)和式(7)。波速vp、vs分别代表P波和SV波波速，E、μ和ρ分别代表半无限介质的弹性模量、泊松比和密度。

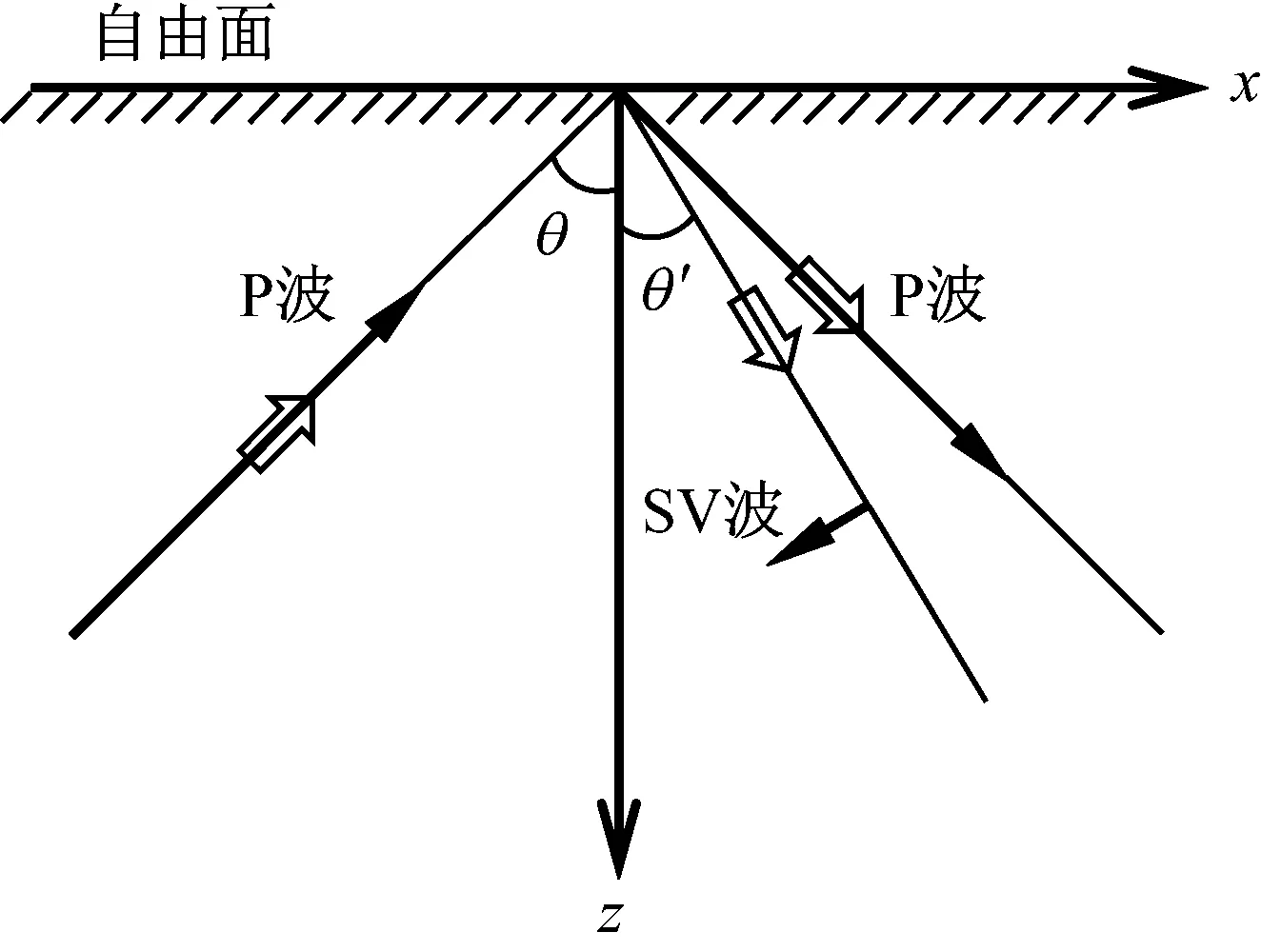
图7 平面P波倾斜入射示意

(6)

(7)

(8)

(9)

4.2 空间特征区域

半无限介质中存在三条地震波，质点运动由三条地震波运动叠加形成。依据与第4节相同的分析方法，可得到在任意空间点(x,z)，入射P波的到达和离开时间PIs和PIe分别表示为式(10)和式(11)，反射P波的到达和离开时间PRs和PRe分别表示为式(12)和式(13)、反射SV波的到达和离开时间SRs和SRe分别表示为式(14)和式(15)。

PIs=(xsinθ-zcosθ)/vp

(10)

PIe=(xsinθ-zcosθ)/vp+T

(11)

PRs=(xsinθ+zcosθ)/vp

(12)

PRe=(xsinθ+zcosθ)/vp+T

(13)

SRs=(xsinθ′+zcosθ′)/vs

(14)

SRe=(xsinθ′+zcosθ′)/vs+T

(15)

由于涉及地震波之间的分离和空间区域的分界，将地震波之间的分离坐标称为分离线，将空间区域的划分坐标称为分界线。依据以上公式，可得出PI与PR的分离线坐标为式(16)、PI与SR的分离线为式(17)、PR与SR的分离线坐标为式(18)。

z1=vpT/2cosθ

(16)

z2=vpvsT/(vpcosθ′+vscosθ)

(17)

z3=vpvsT/(vpcosθ′-vscosθ)

(18)

在三条地震波存在情况下，分离区应满足三条地震波对质点运动时程无重叠贡献时段，因此分界线应为三条分离线中的最大值。考虑到实际场址地震波通常为小角度入射，此时分界线为z3。通过z3表达式可知，当P波倾斜入射时分界线仍与x轴平行。

zd=z3=vpvsT/(vpcosθ′-vscosθ)

(19)

4.3 半无限空间质点运动表达式

图7所示半无限介质内，入射P波的波函数可用式(20)表示，反射P波和反射SV波的波函数可分别用式(21)和式(22)表示。

(20)

(21)

(22)

叠加入射P波、反射P波和反射SV波的波函数，可得到半无限介质内任意空间点运动的水平分量和竖直分量分别为式(23)和式(24)。

h(t,x,z)=g(t,x,z)sinθ+

gp(t,x,z)sinθ-gs(t,x,z)cosθ′

(23)

v(t,x,z)=-g(t,x,z)cosθ+

gp(t,x,z)cosθ+gs(t,x,z)sinθ′

(24)

假设空间坐标由(x,z)变化为(x+Δx,z)，依据式(20)～式(24)和斯奈尔定律式(25)可得到式(26)和式(27)。

vp/vs=sinθ/sinθ′

(25)

(26)

(27)

公式(26)和(27)的物理意义为：在半无限介质内P波倾斜入射情况下，位置(x+Δx,z)处质点的运动，与(x,z)位置质点在Δxsinθ/vp时间后的运动相同。也可描述为质点运动的时程形状不随水平坐标变化。因此研究半无限介质P波倾斜入射情况质点运动空间特征时，可重点关注质点运动沿竖向的变化。相关公式中当θ=0时代表垂直入射情况，因此公式(26)和(27)对P波垂直入射和倾斜入射均适用。

4.4 叠加区运动空间差异

采用与第3节相同的介质参数，假设P波以30°倾斜入射，依据式(19)可得到分界线深度为6.25 km。分别选取自由面和深度2 km质点作为特征点。

图8显示了两个特征点的水平向运动时程，图中时间零点代表地震波传播到达该位置的时刻。当P波以30°入射时，自由面质点运动中入射波和反射波贡献时段都为0～2.00 s；深度2 km处质点运动时程中，入射P波贡献时段为0～2.00 s，反射P波贡献时段为1.61～3.61 s，反射SV波贡献时段为2.25～4.25 s。

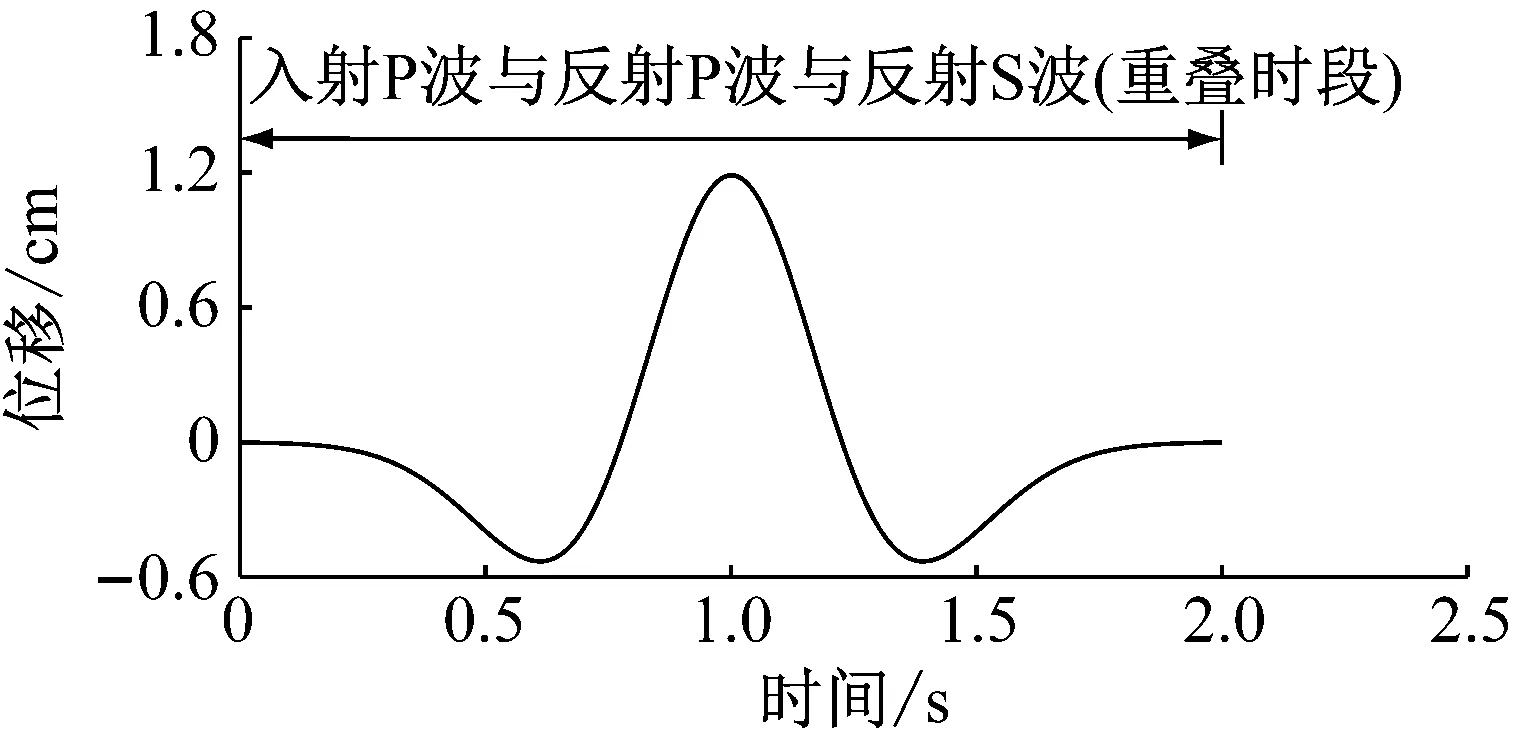
(a) 自由面

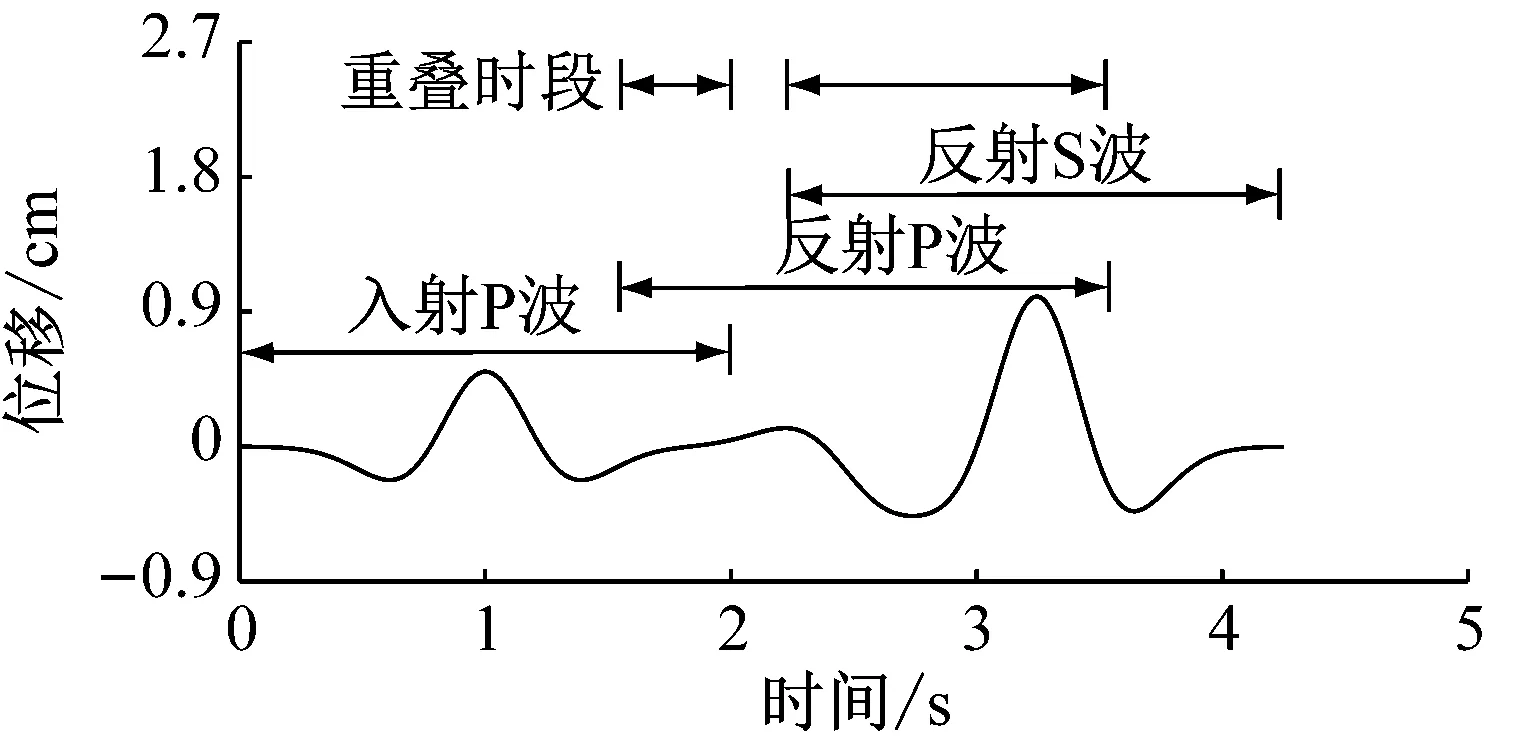
(b) 2 km深度

从质点运动的叠加模式看，质点运动时程可分为单波贡献时段和多波贡献时段。对于自由面质点，整个运动时程均为多波贡献。深度2 km处质点运动时程信息列于表1，在3条地震波影响下，质点运动时程中包含3个单波贡献时段和2个双波贡献时段。

表1 深度2 km质点入射波与反射波贡献时段

Tab.1 Contribution time of incident and reflect waves on motion of particle at 2 kilometers depth

起止时刻/s贡献地震波类型0～1.61PI单波贡献1.61～2.00PI、PR双波贡献2.00～2.25PR单波贡献2.25～2.61PR、SR双波贡献3.61～4.25SR单波贡献

两个位置质点运动时程对比可看出，受到地震波叠加方式的影响，质点运动不仅出现了持时、峰值的差异，也表现出明显的时程形状差异。可见地震波传播效应所带来的地震动空间差异显著且不可忽略。相对于P波垂直入射情况，倾斜入射情况介质内的地震波数量增加，质点运动时程中的地震波贡献时段划分更加复杂。

图9和图10列出了峰值位移沿竖向的分布。可看出倾斜入射表现规律与垂直入射类似，但由于地震波倾斜入射时半无限介质内地震波数量更多且叠加模式更复杂，与垂直入射规律略有不同。以负峰值为例：由于反射P波与反射S波的分离位置更深，倾斜入射情况幅值变化区域较垂直入射更大；由于反射P波与反射S波幅值与入射波幅值不同，位移峰值沿竖向的变化规律与垂直入射情况存在差异。

5 结 论

本文以波动理论为基础，针对平面P波入射时半无限介质内质点运动的空间特征开展研究，得出以下结论：

(1) 平面P波垂直入射和倾斜入射两种情况时，质点运动的空间差异主要沿竖向变化，同高程质点运动仅存在时间滞后，在持时、峰值和时程形状等方面均保持一致。

(2) 平面P波入射时，依据地震波形成质点运动的叠加模式差异，半无限空间沿深度可划分为叠加区和分离区。叠加区主要特征为质点运动时程中存在不同地震波的叠加贡献时段，分离区主要特征为质点运动时程中不同地震波的贡献时段在时域是分离的。依据波的传播条件得到平面P波入射时叠加区和分离区的分界线表达式。

(3) 在叠加区域的不同位置，受到地震波间叠加效应的影响，质点运动在持时、峰值和时程形状方面均可能存在差异。在运动峰值方面，受到入射波和反射波叠加效应影响，接近地面区域均会出现运动峰值随深度减小逐渐增大的现象。

由于本文选取地震波为简单的Ricker子波，只能对地震波传播和叠加模式所产生的质点运动空间差异进行简单的规律性研究。实际地震引起进入场址的地震波更加复杂，该情况下质点运动的空间特征仍需深入研究。