双转子-中介轴承系统非线性振动特性

高 朋， 侯 磊, 2， 陈予恕

(1. 哈尔滨工业大学 航天学院， 哈尔滨 150001； 2. 哈尔滨工业大学 能源科学与工程学院， 哈尔滨 150001)

采用双转子结构的航空发动机因具有较高的推重比和气动稳定性，不易发生喘振等优点，应用较为广泛。但由于中介轴承的引入，使得航空发动机双转子系统振动耦合强烈、非线性突出[1]。

为理清双转子-中介轴承系统的动力学行为，从而提高航空发动机运行稳定性，国内外学者做了许多工作。廖明夫等[2]建立了简支对称的双转子模型，运用解析方法研究了双转子的振动特性，并重点分析了中介轴承的影响，为转子结构设计和中介轴承选择提供了指导准则。周海仑等[3-4]考虑了中介轴承的耦合作用、转静件的碰摩等，建立了双转子航空发动机整机动力学模型。邓四二等[5]采用 Hertz 接触模型模拟中介轴承非线性力，采用 Newmark 法分析了转子转速及轴承参数对双转子系统动力学特性的影响，并进行实验验证。胡清华等[6]建立了五自由度的航空发动机双转子模型，通过与三自由度模型和中介轴承线性化的五自由度模型对比，发现转子的旋转自由度和支撑的非线性对系统的动力学行为有很大影响。罗贵火等[7-8]对比分析了同向和反向旋转双转子系统的拍振响应及轴心轨迹，并通过实验验证了理论结果。Ferraris 等[9]分析了刚度阵非对称的反向旋转双转子的动力学特性，得到了临界转速、不平衡响应曲线以及进动方向的变化规律。符毅强等[10]建立了考虑中介轴承非线性力的反向旋转双转子系统简化模型，通过数值求解发现系统的幅频响应存在明显的共振滞后现象，并分别讨论了转速比，中介轴承径向游隙以及阻尼比对系统滞后特性的影响。孙传宗等[11]针对某型航空发动机双转子-支承系统进行了高精度三维实体有限元建模，并提出了基于 Craig-Bampton 固定界面模态综合法的模型缩减技术，可大大降低整机模型的自由度数，并且该方法具有计算精度高、收敛性好、易于和其他程序衔接等优点。路振勇等[12-13]提出了航空发动机双转子-支承系统的工程降维技术，基于惯性等效原则对系统进行结构简化，得到的简化模型能够较好地保有原系统的动力学特性，这为航空发动机双转子系统的简化建模提供了新的技术途径。Hou等[14]引入 HB-AFT 法求解双转子-中介轴承非线性模型，研究了转速比、不平衡激励及中介轴承径向游隙对系统主共振幅频特性的影响。

振动突跳作为航空发动机转子系统基本故障特征之一[15]，影响着航空发动机的运行稳定性。本文基于航空发动机双转子-中介轴承系统简化模型，研究中介轴承 Hertz 接触力对系统耦合振动的影响，重点关注由于中介轴承的本质非线性特征引起的系统振动突跳与双稳态特性，并分析转子偏心距、转速比以及中介轴承刚度、滚子数目和径向游隙等主要结构参数对系统振动突跳及双稳态特性的影响规律。

1 双转子-中介轴承系统动力学模型

1.1 双转子系统模型

根据文献[13]动力学模型简化方法，将某四点支承的双转子航空发动机简化成四点支承的双盘转子系统，如图 1 所示。其中高压转子与低压转子通过中介轴承联接在一起，中介轴承为圆柱滚子轴承，包含分数指数型Hertz接触力、径向游隙和接触刚度周期性变化引起的参数激励等非线性因素。此外，低压转子两端支承以及高压转子左端支承均简化为线性弹性支承。

图1 双转子中介轴承模型

现考虑高压转子和低压转子均为刚性转子，给出各能量表达式[16]

系统动能

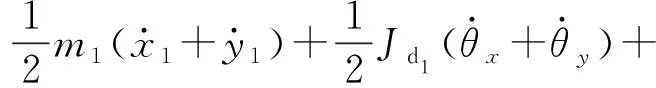
(1)

系统势能

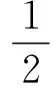
m1gx1+m2gx2

(2)

瑞利耗散函数

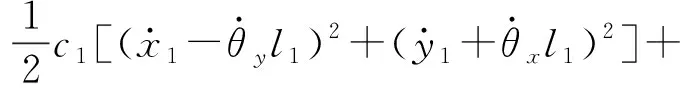
(3)

广义力虚功

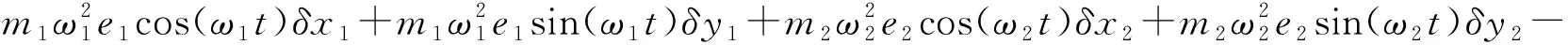
Fx{[δx1+δθy(l2-l5)]-(δx2+δφyl4)}-

Fy{[δy1-δθx(l2-l5)]-(δy2-δφxl4)}

(4)

式中：无特殊说明时下标1表示低压转子，下标2表示高压转子；m，Jp，Jd，e，ω分别表示盘的质量、极转动惯量、直径转动惯量、偏心距和转速；x，y分别表示盘心竖直位移和水平位移；θx，θy分别表示低压盘绕x轴转动角度和绕y轴转动角度；φx，φy分别表示高压盘绕x轴转动角度和绕y轴转动角度；ki，ci(i= 1～3)分别表示弹性支承的刚度系数和阻尼系数；Fx，Fy分别表示中介轴承竖直方向和水平方向的弹性恢复力；δ·表示对应广义坐标下的虚位移。

1.2 中介轴承弹性恢复力模型

中介轴承的弹性恢复力采用Hertz接触力模型。图 2 表示中介轴承运动示意图。其中，ri和ro分别为轴承内圈半径和外圈半径，Nb为圆柱滚子数目，θk为第k个滚子的角位置。由于内圈与低压转轴固连，外圈与高压转轴固连，因此内、外圈转速分别为ω1和ω2。此外，ωc为保持架转速。

假设内、外圈分别与低压转子、高压转子过盈配合，滚子在内、外圈之间做纯滚动，则保持架转速可表示为

(5)

式中:ri、ro分别表示轴承内、外圈半径。

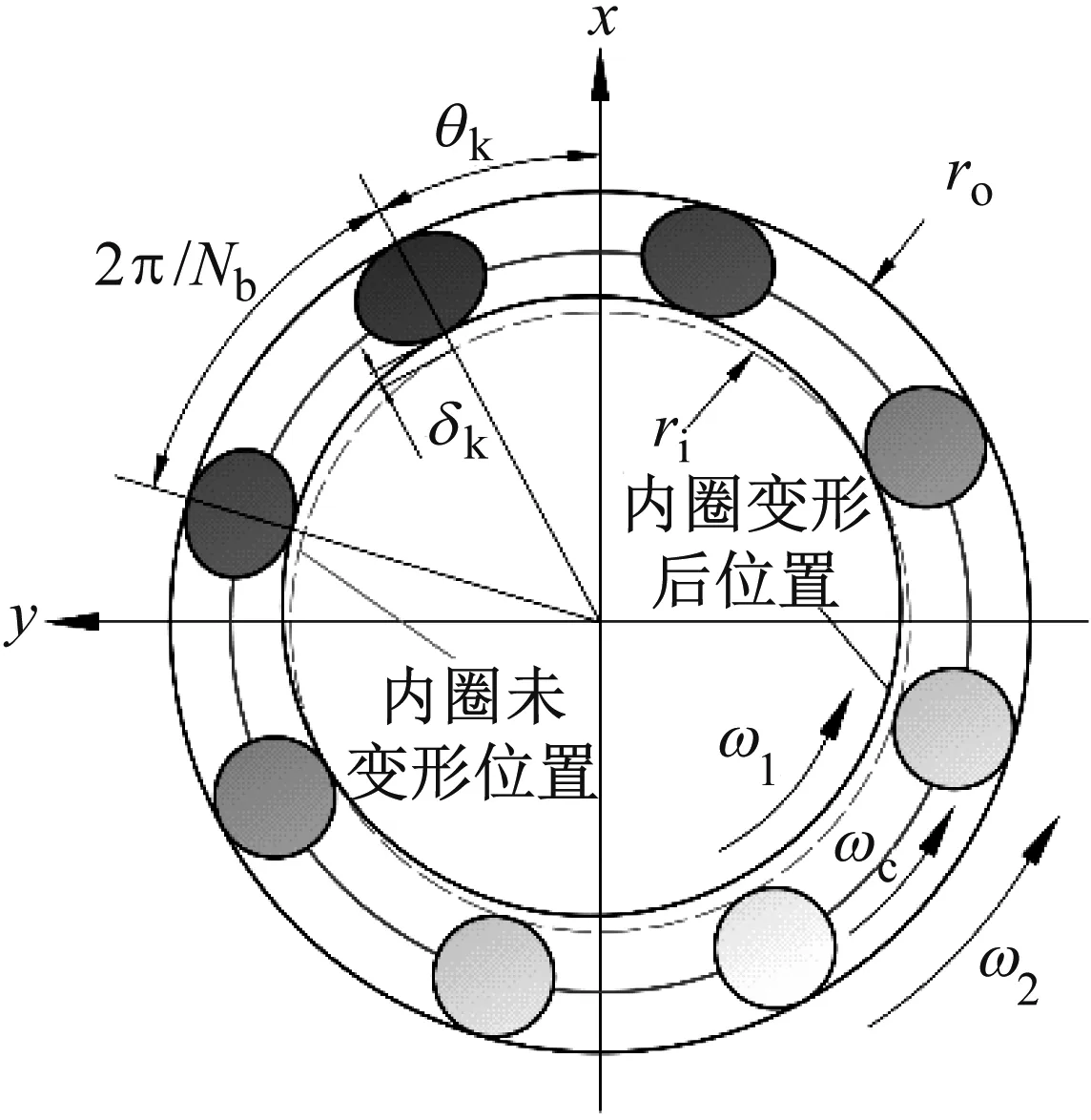
图2 中介轴承示意图

任意时刻t，第k个滚子的瞬时角位置

(6)

式中：Nb表示滚子数目。

在小变形前提下，第k个滚子与轴承内圈和外圈的相对接触变形可以表示为

δk=(xi-xo)cosθk+(yi-yo)sinθk-δ0=

{[x1+θy(l2-l5)]-(x2+φyl4)}cosθk+

{[y1-θx(l2-l5)]-(y2-φxl4)}sinθk-δ0，

k=1,2,…,Nb

(7)

式中:xi、xo、yi、yo分别表示轴承内、外圈在竖直、水平方向位移分量，2δ0表示轴承径向游隙。

根据Hertz接触理论，第k个滚子提供的弹性恢复力为

公元2311年的一次拍卖会上，一件收藏品被拍到了天价。据称这套藏品对研究三百年前那个时代具有极高的学术价值，它囊括了当年某人从出生证、学生证、毕业证、体检合格证、工作证、结婚证、准生证、独生子女证、房产证、税务登记证……一直到死亡证所必备的301个证件。

(8)

进而，中介轴承提供的弹性恢复力为

(9)

1.3 系统运动微分方程

利用Lagrange第二方程，根据式(1)～(4)可推导出系统运动微分方程如下

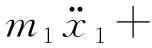
k1(x1-θyl1)+k2(x1+θyl2)=

(10)

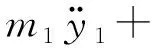
(11)

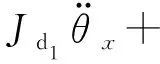
Fy(l2-l5)

(12)

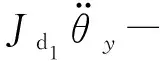
(13)

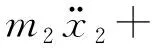
(14)

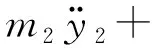
(15)

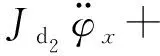
k3l3(y2+φxl3)=-Fyl4

(16)

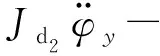
k3l3(x2-φyl3)=Fxl4

(17)

1.4 方程的无量纲化

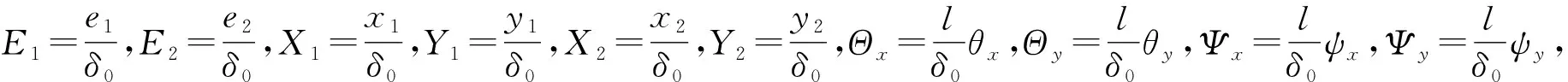
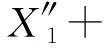
K1(X1-L1Θy)+K2(X1+L2Θy)=

(18)

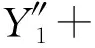
(19)

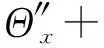
K3(Y1+L1Θx)-K4(Y1-L2Θx)=

(20)

K3(X1-L1Θy)+K4(X1+L2Θy)=

(21)

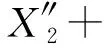
(22)

(23)

(24)

(25)

{[X1+Θy(L2-L5)]-(X2+ΨyL4)}cosθk+

{[Y1-Θx(L2-L5)]-(Y2-ΨxL4)}sinθk-1，

k=1,2,…,Nb

整理无量纲方程(18)～(25)为如下矩阵形式

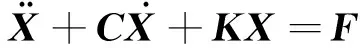
(26)

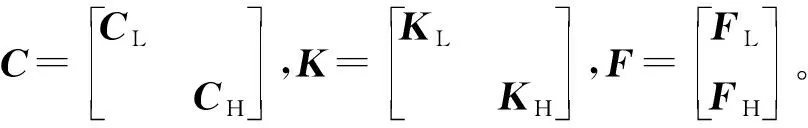
2 系统参数及振幅的定义

2.1 双转子-中介轴承系统参数

本文采用4阶 Runge-Kutta 法对双转子-中介轴承模型进行数值计算，分析系统的幅频响应特性，尤其是振动突跳与双稳态特性。所采用的模型参数[17]如下：

双转子参数：

m1= 97.37 kg,m2= 108.30 kg,Jp1=3.690 7 kg/m-2,Jd1=1.845 4 kg/m-2,Jp2= 4.011 9 kg/m-2,Jd1=2.006 0 kg/m-2,k1=k2=k3= 6×107N/m,c1=c2=c3=655 N·s/m,l1= 0.918 8 m,l2= 1.112 2 m,l3= 0.512 0 m,l4= 0.624 3 m,l5=0.099 5 m,e1= 3 μm,e2= 2 μm, 转速比λ= 1.2。

中介轴承参数：

ri= 58 mm,ro= 66 mm,Nb= 8,Kb= 108N/m10/9,2δ0= 10 μm。

2.2 振幅的定义

由于双转子系统承受高低压转子的双频不平衡激励，响应中存在至少两种频率成分，本文采用反映振动信号能量的有效值表示常规幅频曲线中的振幅，其中，低压转子幅值定义如下

(27)

高压转子幅值定义如下

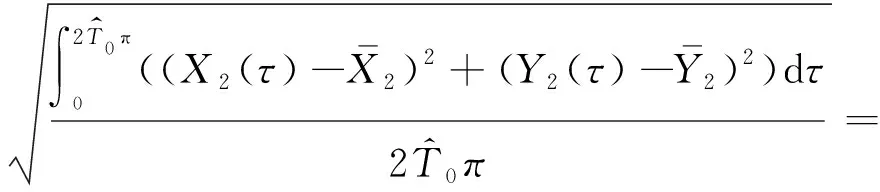
(28)

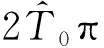
(29)

其中假设m和n互为质数，则合成信号为周期振动，其周期为

(30)

2.3 系统临界转速及振型分析

根据文献[19]，绘制出双转子系统正向涡动时前2阶的坎贝尔图，如图 3所示，其中λ= 1.2表示转速比为1.2时的高低压转子共同工作线。双转子系统的坎贝尔图较单转子系统的坎贝尔图更加复杂，双转子系统的每一阶临界转速可以分为以高压转子为主激励的临界转速和以低压转子为主激励的临界转速。从图中可以看出，当高低压转子保持恒定转速比转动，随着转速的提高，首先发生高压转子主共振(第一阶临界转速)，然后发生低压转子主共振。若转速继续提高，则会依次发生二阶高压转子共振，二阶低压转子共振。

图3 转速比1.2时系统坎贝尔图

本文双转子简化模型中假设高低压转子均为刚性转子，并且本文重点关注主共振区，即一阶临界转速附近系统非线性特征，现给出系统一阶振型，如图 4所示。可以看出，双转子系统在一阶临界转速附近主要以横向振动为主。

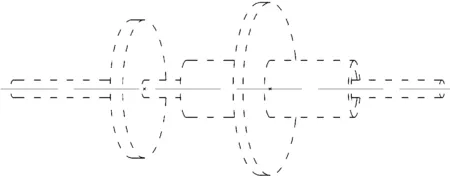
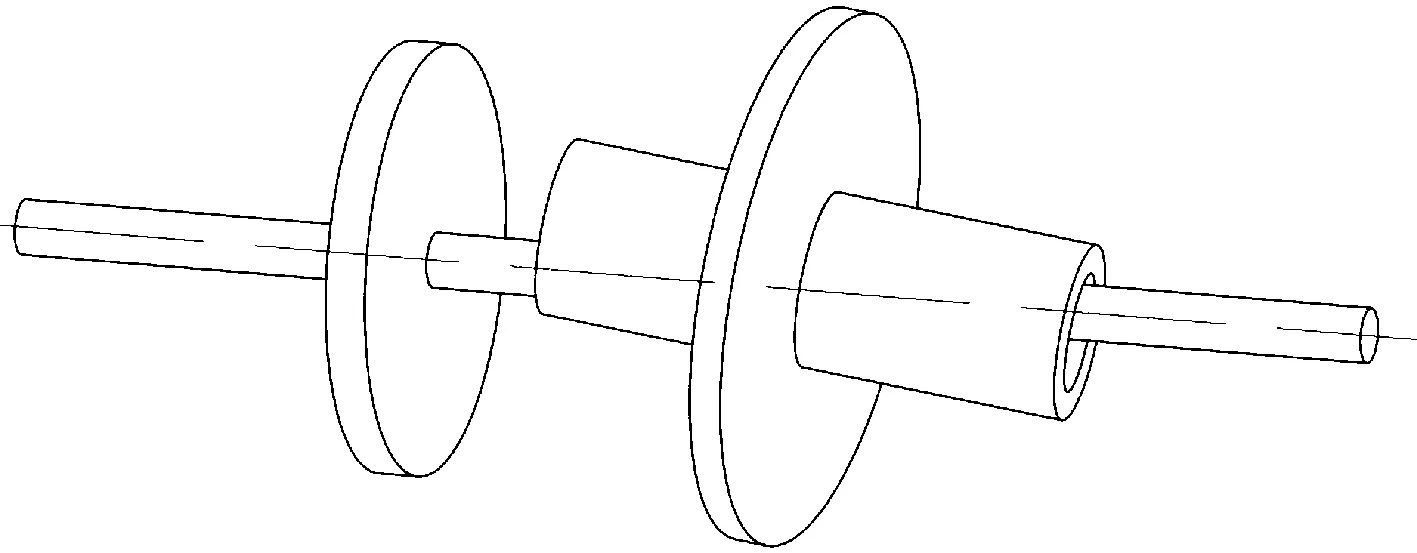
图4 双转子系统一阶振型

3 数值计算结果及分析

3.1 系统幅频响应的振动突跳与与双稳态特性

利用 Matlab 中4阶Runge-Kutta法对公式(26)进行求解，并将无量纲坐标转化为原有物理坐标，根据幅值定义，高低压转子幅频曲线可以绘出。为了便于比较高低压转子幅频曲线的异同，选取低压转子转速ω1作为高低压转子幅频曲线的横坐标。为了考察系统主共振幅频特性，截取一阶临界转速附近转速区间的幅频曲线，如图 5 所示，图 5 (a)、(b)分别为低压转子、高压转子一阶临界转速附近幅频曲线。

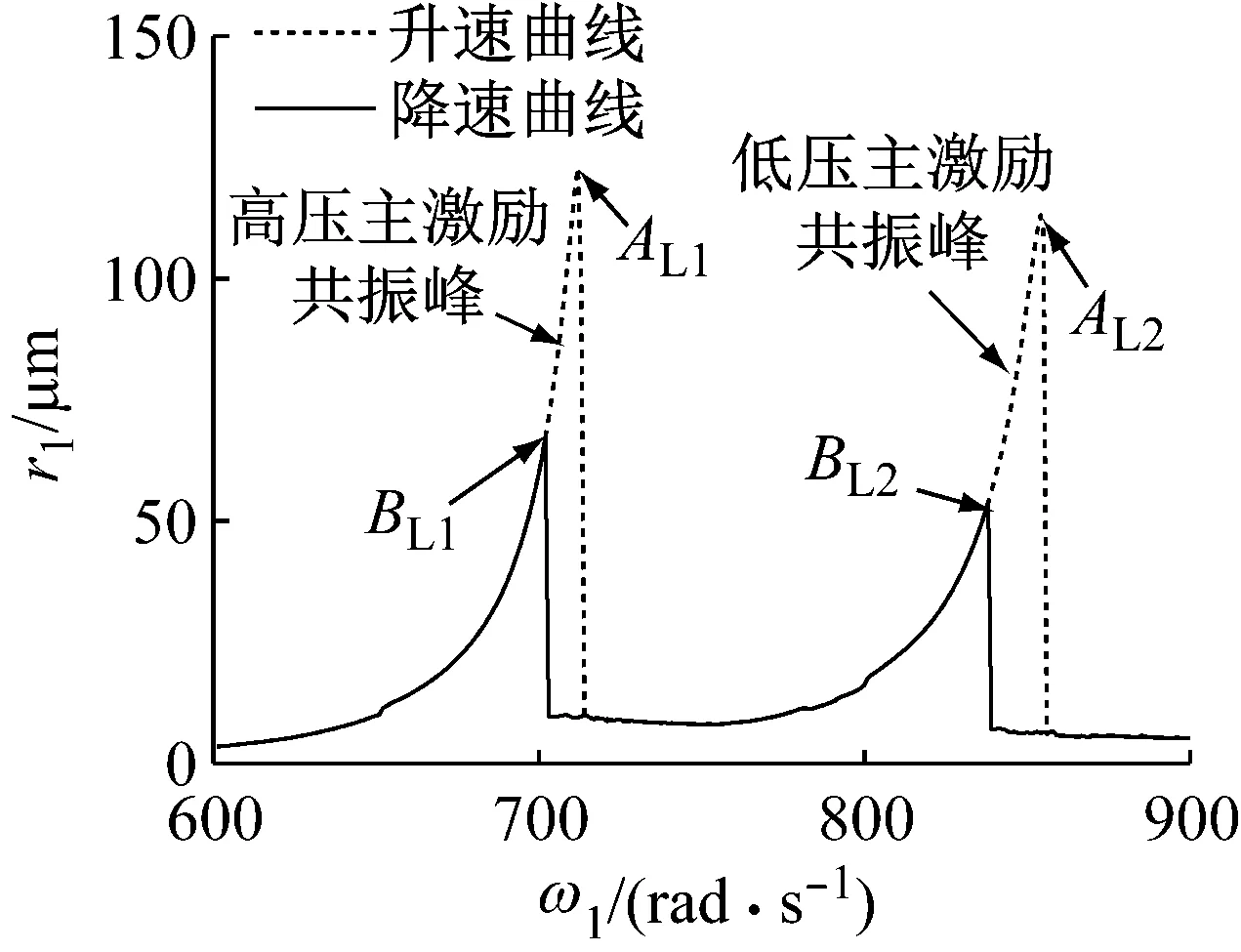
(a) 低压转子的幅频响应曲线

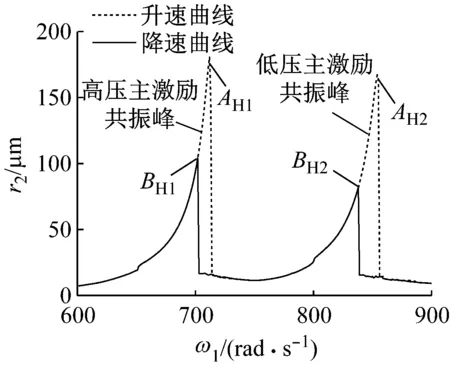
(b) 高压转子的幅频响应曲线

由图 5 可以看出，高低压转子的升速过程和降速过程，都会出现两个共振峰，其中第一个共振峰为高压转子通过临界转速激起的共振峰，第二个共振峰为低压转子通过临界转速激起的共振峰；同时，在共振峰处，均会出现明显的振动突跳和双稳态现象。在升速过程突跳点A与降速过程突跳点B之间，形成双稳态区间。对比图 5 (a)和(b)，可发现高压转子幅频曲线共振峰值明显大于低压转子幅频曲线共振峰值。

系统之所以出现振动突跳和双稳态等典型非线性特征，是因为中介轴承弹性恢复力具有本质非线性特征，由式(9)可知，中介轴承弹性恢复力存在分数指数非线性、径向游隙和参数激励等多种非线性因素。研究发现，分数指数非线性及径向游隙单独存在时，系统均可能会出现振动突跳和双稳态现象，但现象并不明显，当二者耦合时，会加强这种非线性特征，出现明显的振动突跳和双稳态现象。

通过分析高低压转子幅频曲线的共振峰值点的转速ωAL1，ωAL2，ωAH1，ωAH2的大小关系，可以发现如下规律

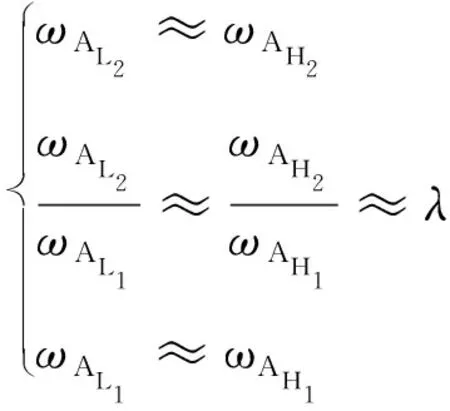
(31)

高低压转子的幅频响应曲线中低压主激励共振峰值点与高压主激励共振峰值点比值约等于转速比，也就是说转速比决定了两个共振峰值点的相对位置。

3.2 转子偏心距的影响

首先分析低压转子偏心距的影响，低压转子偏心距分别取为e1= 2 μm，e1= 3 μm，e1= 4 μm和e1= 5 μm，对比高压转子幅频曲线，如图 6 (a)所示，可见，e1的变化对高压主激励共振峰基本无影响。进一步分析e1的变化对低压主激励共振峰的影响，截取图 6 (a)中低压主激励共振峰并放大，如图 6 (b)所示，可见，随着e1的增大，低压主激励共振峰值点右移，表明系统临界转速提高；同时峰值响应增大，伴随着升速、降速突跳幅度均增大，但双稳态区间却变窄。此外，低压转子幅频曲线也有与此相似的变化规律。

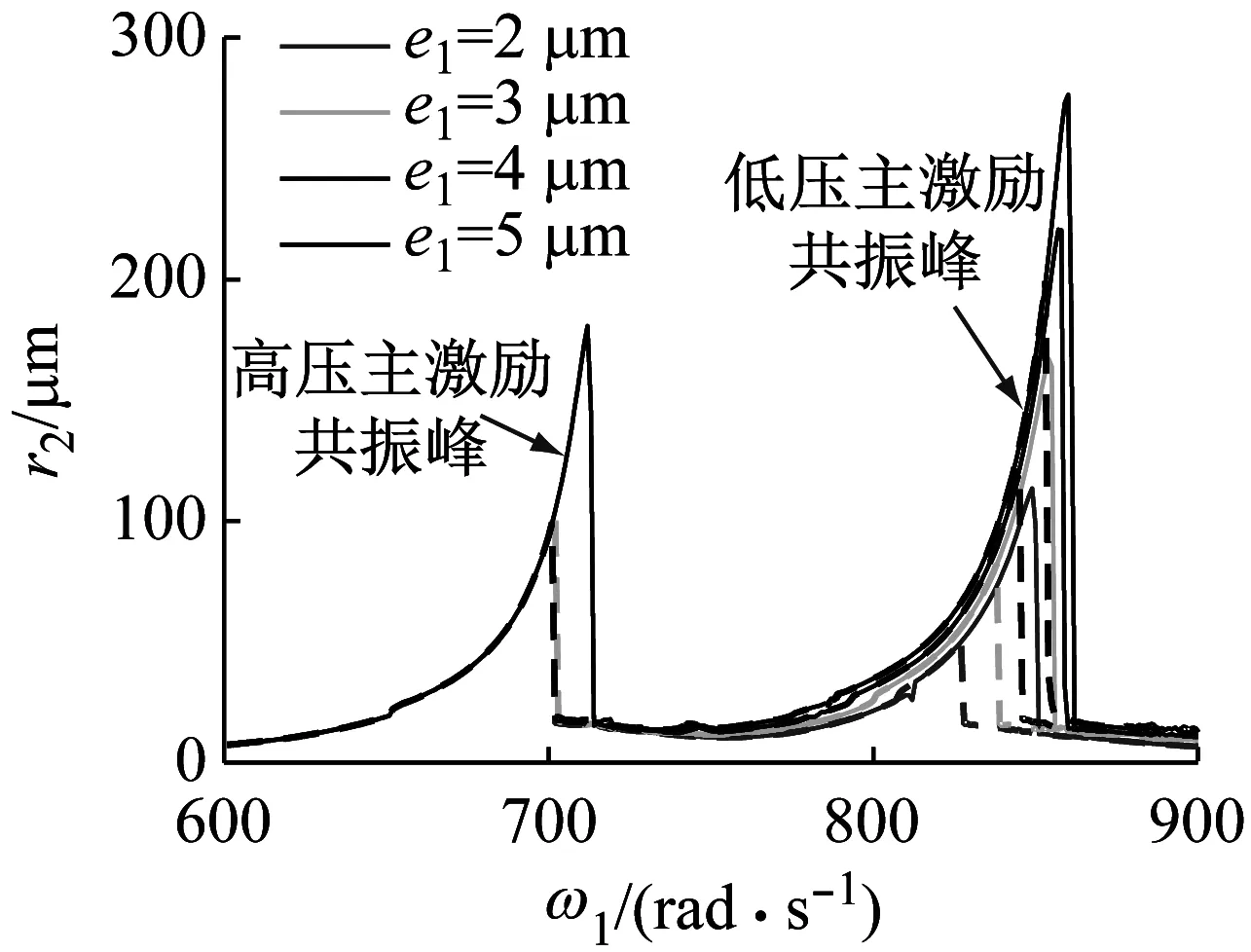
(a) 全局图

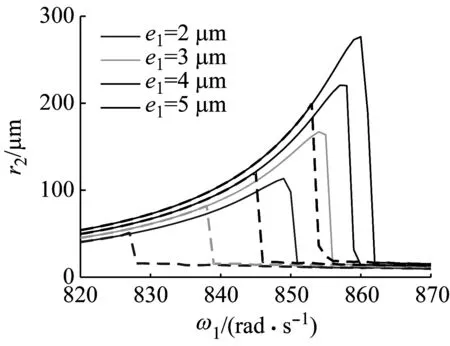
(b) 低压主激励共振峰局部放大图

Fig.6 Comparison of higher-pressure-rotor’s amplitude frequency curves under different lower-pressure-rotor’s eccentricity

然后分析高压转子偏心距的影响，高压转子偏心距分别取为e2= 2 μm，e2= 3 μm，e2= 4 μm和e2= 5 μm，对比高压转子幅频曲线，如图 7 (a)所示，可见，e2的变化对低压主激励共振峰基本无影响。进一步分析e2的变化对高压主激励共振峰的影响，截取图 7 (a)中高压主激励共振峰并放大，如图 7 (b)所示，可见，随着e2的增大，高压主激励共振峰值点右移，表明系统临界转速提高；同时峰值响应增大，伴随着升速、降速突跳幅度均增大，但双稳态区间却变窄。此外，低压转子幅频曲线也有与此相似的变化规律。

偏心距增大意味着系统的不平衡激励增大，从能量角度考虑相当于外界能量输入增加，共振峰显然增大。偏心距对于非共振区域基本无影响，故系统升速、降速跳跃幅度都会增大。

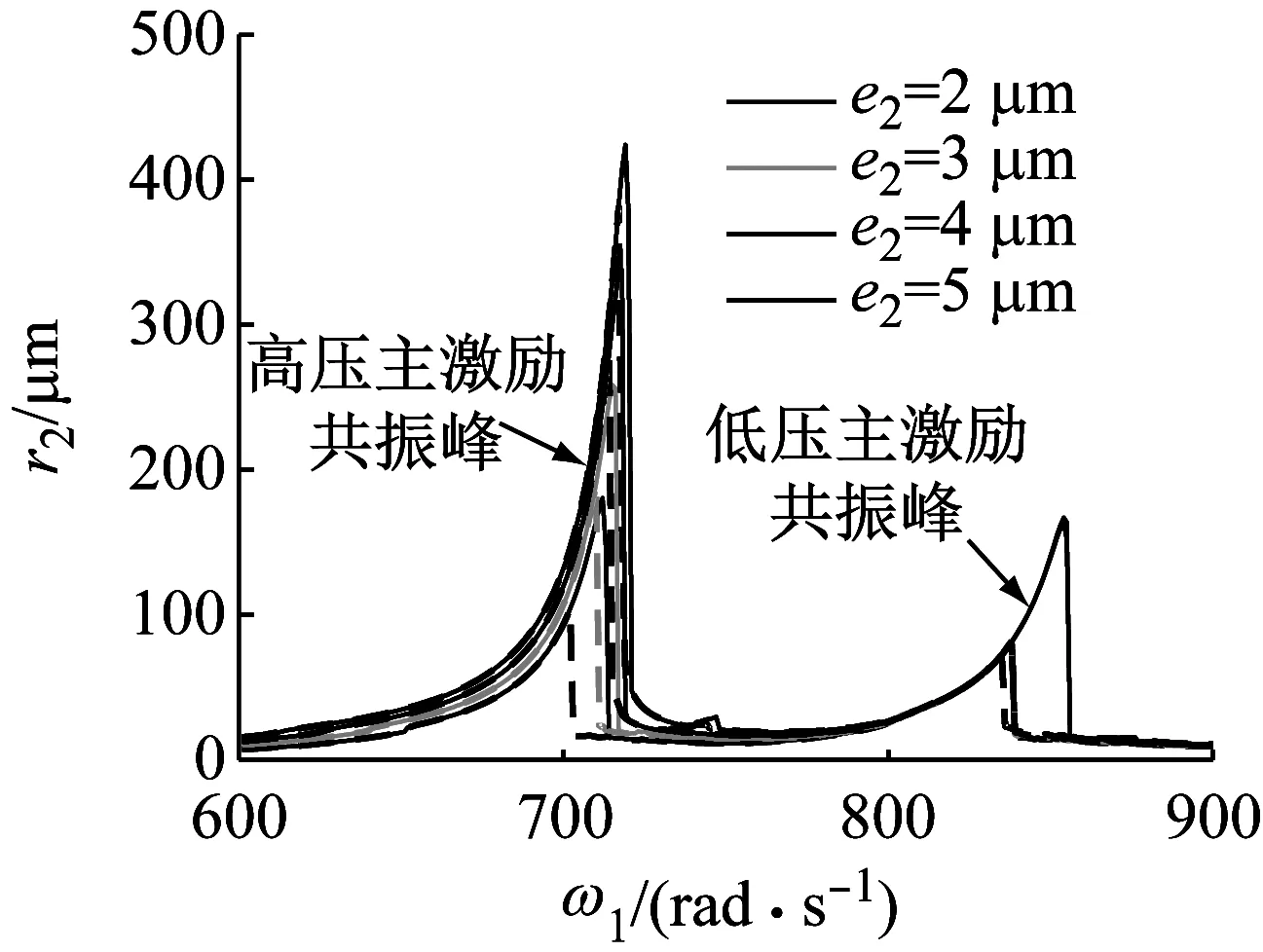
(a) 全局图

(b) 高压主激励共振峰局部放大图

Fig.7 Comparison of higher-pressure-rotor’s amplitude frequency curves under different higher-pressure-rotor’s eccentricity

为了分析偏心距增大，临界转速提高这一现象，现引入中介轴承“动态刚度”这一概念。由于不平衡激励属于交变载荷，其“动态刚度”相比于其静刚度更能描述该滚子当前时刻的刚度情况。根据式(9)，中介轴承所提供的弹性恢复力为

(32)

则其“动态刚度”Kdynamic可以表示为

(33)

根据式(33)可知，δ越大，Kdynamic越大。所以当偏心距增大时，中介轴承接触变形δk也就越大，故中介轴承“动态刚度”也随之增大，系统临界转速增大。

因此，提高高低压转子动平衡精度，减小偏心距，能有效降低系统共振峰值并抑制振动突跳行为，但同时会降低中介轴承“动态刚度”，从而使系统双稳态区间变宽。

3.3 转速比的影响

图 8 为不同转速比下高压转子的幅频曲线对比，转速比分别取λ= 1.1，λ= 1.15，λ= 1.2和λ=1.3。可见，随着λ的增大，低压主激励共振峰基本无变化，表明转速比对系统临界转速基本无影响；而高压主激励共振峰值点大幅度左移，但两个共振峰值点转速大小仍满足式(31)，表明转速比决定了两个共振峰的相对位置；两个共振峰值响应，升速、降速突跳幅度以及双稳态区间均无明显变化。此外，低压转子幅频曲线也有与此相似的变化规律。

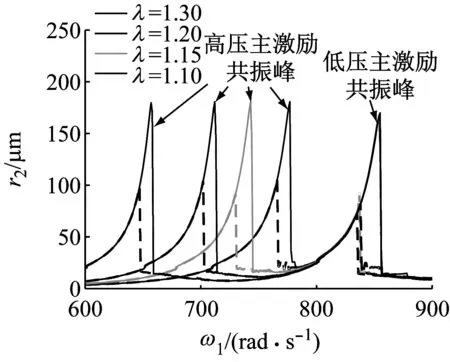
(——升速曲线，----降速曲线)

Fig.8 Comparison of higher-pressure-rotor’s amplitude frequency curves under different rotational speed ratio

3.4 中介轴承刚度的影响

中介轴承不仅是高低压转子的联接部件，也是高压转子的支承部件，是引起高低压转子强烈耦合运动的根源[20]，因而中介轴承结构参数对双转子系统的振动特性产生至关重要的影响。下文对中介轴承刚度、滚子数目和径向游隙等主要结构参数对系统振动特性的影响展开研究。

图 9 (a)、(b)分别为不同中介轴承刚度下低压转子、高压转子幅频曲线对比，其中中介轴承刚度分别取Kb= 0.8Kb0，Kb=Kb0，Kb= 1.5Kb0和Kb= 2Kb0，其中Kb0= 108N/m10/9。对比图 9 (a)和(b)，相同的现象有：随着Kb的增加，共振峰值点均右移，表明系统临界转速提高，同时双稳态区间也随之变窄。不同的现象有：随着Kb的变化，低压转子幅频曲线中低压主激励共振峰的变化幅度明显大于高压主激励共振峰，而高压转子幅频曲线中高压主激励共振峰的变化幅度明显大于低压主激励共振峰，表明低压转子幅频曲线中低压主激励共振峰以及高压转子幅频曲线中高压主激励共振峰对于中介轴承刚度的变化更加敏感。因此，增大中介轴承刚度会显著提高系统临界转速，同时也会使双稳态区间变窄。

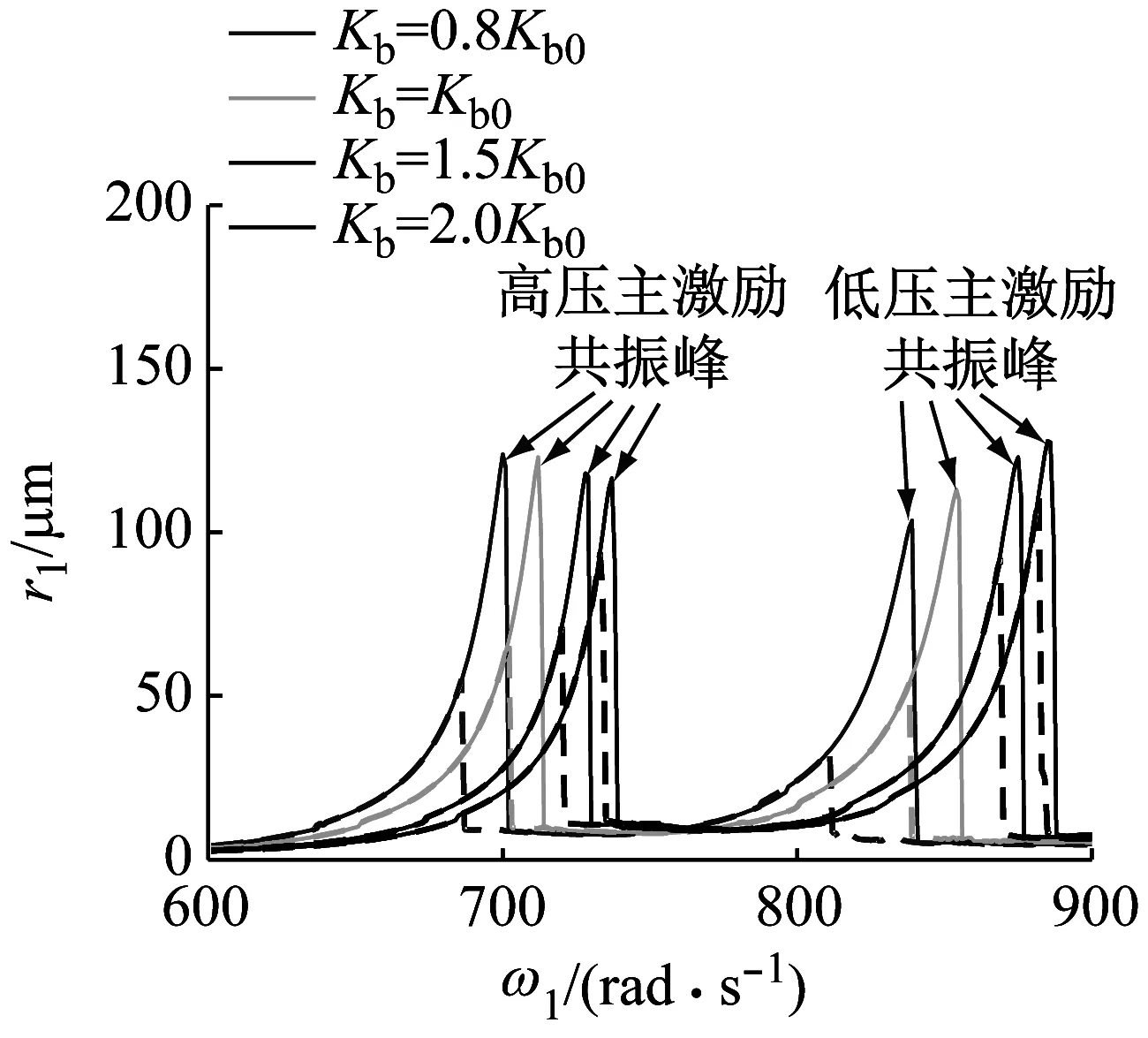
(a) 低压转子

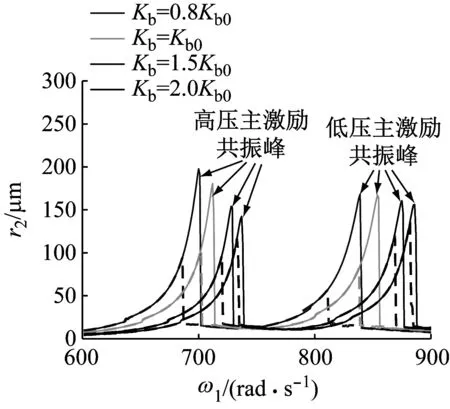
(b) 高压转子

3.5 中介轴承滚子数目的影响

图 10 (a)、(b)分别为不同中介轴承滚子数目下低压转子、高压转子幅频曲线对比，其中滚子数目分别取Nb= 6，Nb= 8，Nb= 10和Nb= 12。对比图 10 (a)和(b)，相同的现象有：随着Nb的增加，共振峰值点均右移，表明系统临界转速提高，同时双稳态区间也随之变窄。不同的现象有：随着Nb的变化，低压转子幅频曲线中低压主激励共振峰的变化幅度明显大于高压主激励共振峰，而高压转子幅频曲线中高压主激励共振峰的变化幅度明显大于低压主激励共振峰，表明低压转子幅频曲线中低压主激励共振峰以及高压转子幅频曲线中高压主激励共振峰对于滚子数目的变化更加敏感。

值得注意的是，中介轴承滚子数目对系统振动突跳和双稳态特性的影响效果与中介轴承刚度影响效果类似。在中介轴承产生相同接触变形的情况下，随着滚子数目的增加，中介轴承同一时刻产生接触变形的滚子就会越多，中介轴承提供弹性恢复力也会越大，中介轴承刚度也就越大。因而，增加滚子数目效果等同于增加中介轴承刚度。

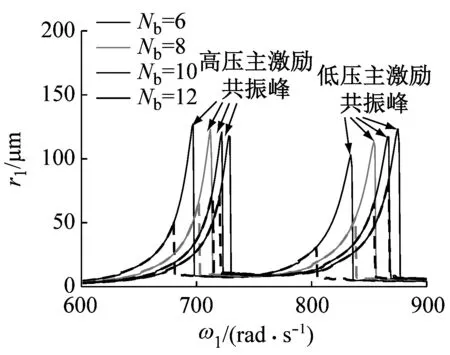
(a) 低压转子

(b) 高压转子

因此，在一定范围内，增大中介轴承滚子数目相当于间接增加中介轴承刚度，从而提高系统临界转速，同时双稳态区间也会变窄。

3.6 中介轴承径向游隙的影响

图 11 (a)、(b)分别为不同中介轴承径向游隙下低压转子、高压转子幅频曲线对比，其中径向游隙分别取2δ0= 4 μm，2δ0= 10 μm，2δ0= 20 μm和2δ0= 30 μm。对比图 11 (a)和(b)，相同的现象有：随着δ0的增大，共振峰值点均左移，表明系统临界转速降低，同时双稳态区间也明显变宽。不同的现象有：随着δ0的变化，低压转子幅频曲线中低压主激励共振峰的变化幅度明显大于高压主激励共振峰，而高压转子幅频曲线中高压主激励共振峰的变化幅度明显大于低压主激励共振峰，表明低压转子幅频曲线中低压主激励共振峰以及高压转子幅频曲线中高压主激励共振峰对于径向游隙的变化更加敏感。值得注意的是，当径向游隙增大到一定程度时，系统的运动状态将变得更加复杂，如当径向游隙为30 μm时，系统在非主共振区也发生了振动突跳与双稳态现象。

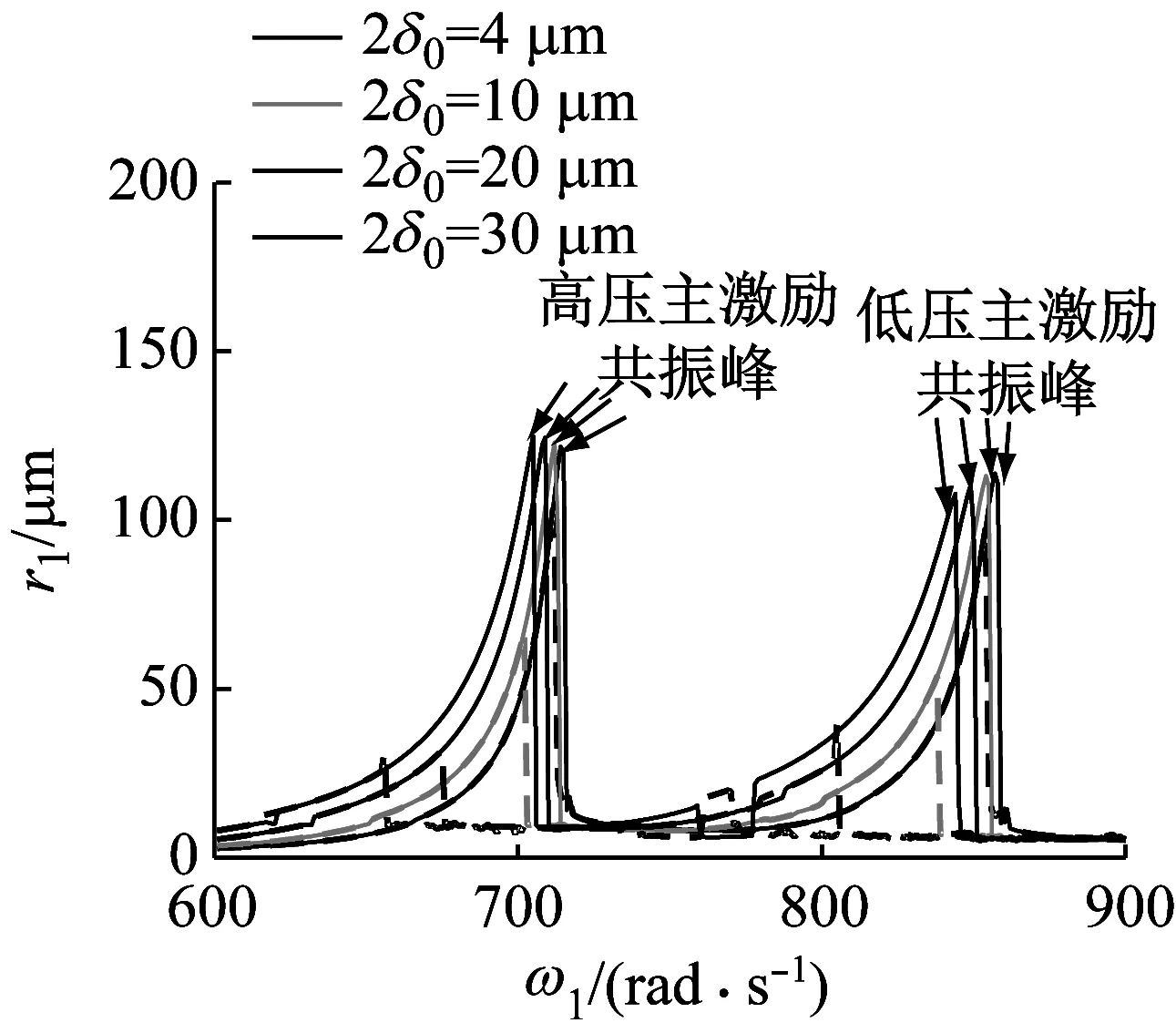
(a) 低压转子

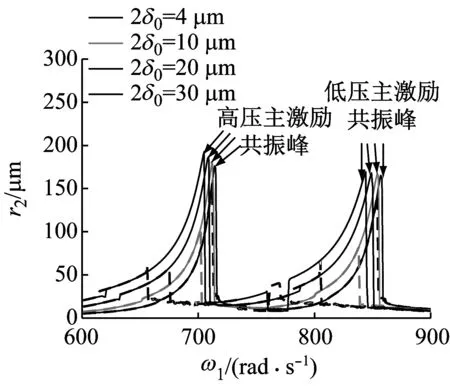
(b) 高压转子

中介轴承径向游隙的存在，使得滚子与内外滚道的接触时间产生延迟，相当于变相地降低了中介轴承刚度[21]，系统临界转速也略微随之降低；同时，径向游隙是一种本质非线性特征，双稳态区间也随之变宽。因此，适当减小中介轴承径向游隙能使系统的双稳态区间显著变窄。

4 结 论

本文考虑中介轴承分数指数非线性、径向游隙和参数激励等多种非线性因素，建立了航空发动机双转子-中介轴承系统简化模型，并采用4阶Runge-Kutta法对模型进行求解，得到了双转子-中介轴承系统幅频响应曲线，并详细讨论了偏心距、转速比、中介轴承刚度、滚子数目和径向游隙对系统振动突跳与双稳态特性的影响。主要结论如下：

(1) 高低压转子由于转速不一致造成先后两次通过第一阶临界转速，引起幅频响应曲线上出现两个共振峰，在中介轴承非线性传递力的作用下形成两个共振区间，且均表现出振动突跳与双稳态特性。

(2) 减小高低压转子偏心距，能有效降低系统共振峰值并抑制振动突跳行为，但双稳态区间会变宽。

(3) 高低压转子的转速比决定了两个共振峰的相对位置，随着转速比的增大，低压主激励共振峰位置不变，而高压主激励共振峰左移，但两者比值仍等于转速比。

(4) 增大中介轴承刚度能够使系统双稳态区间变窄，同时会显著提高系统临界转速。

(5) 在一定范围内，增大中介轴承滚子数目相当于间接增加中介轴承刚度，从而使系统双稳态区间变窄，同时提高系统临界转速。

(6) 中介轴承径向游隙增大能使系统的双稳态区间显著变宽，同时会使得系统更易发生振动突跳与双稳态现象。

后续的研究将主要集中在中介轴承故障对双转子系统非线性特性的影响。