基于弹性力学的端部有裂缝悬臂梁的自由振动分析

蒋 杰， 周 叮， 胡朝斌

(南京工业大学 土木工程学院，南京 211816)

在土木、航天等领域中，许多复杂构件常常简化为梁式构件进行分析，如汽轮机的叶片和飞机的机翼等。由于在长期复杂的受力环境下，梁构件可能会产生裂缝，从而降低结构的刚度，导致固有频率下降和响应增大。众所周知，悬臂梁的端部因承受弯矩最大，极易产生裂纹。Chondros等[1]将悬臂梁端部带裂纹截面的抗弯能力等效为扭转弹簧，其弹簧刚度大小与裂纹的深度紧密相关。Bamnios等[2]通过理论和实验研究发现等效扭转弹簧法仅适用于悬臂梁端部裂缝深度较小的情况，对于深裂纹该模型会产生较大的误差。Yokoyama等[3]采用线性扭转弹簧模拟任意位置处的裂纹，结合Euler-Bernoulli梁理论和能量法建立自由振动控制方程，得到的固有频率与实验结果吻合良好。然而，裂纹梁的主变形是连续的，弹簧模型无法考虑到裂纹周围的应力释放。Shen等[4]通过引入裂缝函数对裂缝引起的应力场进行修正，建立了含有浅裂纹的Euler-Bernoulli梁的运动方程，用伽辽金法和局部利兹法得到自振频率和相应的振型。Chondros等[5]建立了连续裂缝梁理论模型。结果表明，连续裂缝梁模型比等效扭转弹簧模型更接近于实验结果。Ebrahimi等[6]基于该理论模型，分析了含有纵向或横向裂纹梁的动力特性，与有限元对比显示出很好的一致性。杨鄂川等[7-8]基于连续梁理论模型，分析了旋转运动和轴向运动效应下裂纹梁的横向振动特性。由于Euler-Bernoulli梁理论只适用于长细比较小的细长梁，对于中厚梁，需考虑剪切变形和转动惯量的影响，可采用Timoshenko梁理论来描述梁的变形。Swamidas等[9]分析得出，当l/h>10时采用Euler-Bernoulli梁理论和Timoshenko梁理论得到的结果相似，当l/h<10时则二者结果误差较大，Timoshenko梁理论的结果更接近真实值。徐福后等[10]基于传递矩阵法分析含裂纹Timoshenko梁自由振动特性，数值计算结果验证了该方法的有效性。Liu等[11]分析了带有斜裂缝悬臂梁的自由振动特性。马辉等[12]使用有限元法分析了非对称夹持的裂缝悬臂梁的振动响应。由上述文献可知，国内外学者很少对梁端部裂纹进行精确分析。对于长细比更小的梁，Timoshenko梁理论仍会产生较大误差，此时须采用更为精确的弹性力学理论进行分析求解。

本文基于精确的二维弹性力学理论，分析端部有裂缝悬臂梁的自由振动特性。在裂纹尖端处将裂纹梁沿水平方向划分为边界条件不同的两层子梁，采用Chebyshev-Ritz[13-14]法建立每一层梁的二维振动特征方程，通过上下层沿交界面的位移连续性条件得到整个悬臂梁的振动特征方程。方法可以很好地分析端部有裂纹厚梁的固有振动特性。

1 端部裂缝悬臂梁的振动分析

1.1 悬臂梁模型和每层梁的动力学公式

考虑如图1所示的悬臂梁，长为L，高为h，宽为b，密度为ρ，泊松比为v，弹性模量为E，悬臂梁的端下部有裂缝，深度h1。设x方向的位移分量为u，z方向的位移分量为w，建立如图1所示的分析模型。

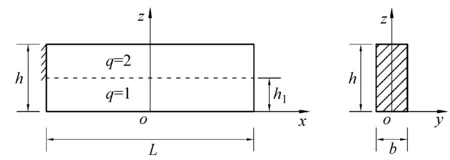
图1 端部有裂缝悬臂梁的分析模型

悬臂梁体积域的取值范围为

(1)

不失一般性，考察第q(q=1，2)层梁的振动特性，其线弹性应变能Vq如下：

(2)

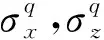
考虑x-z平面的应力-应变关系如下：

(3)

(4)

(5)

将式(3)～(5)代入式(2)得：

(6)

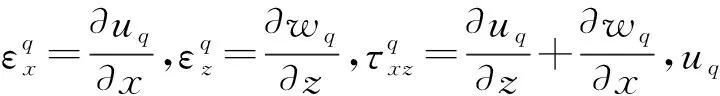
第q层梁的动能Tq为

(7)

为了数学形式上的简化，将x，z坐标作无量纲化处理，即：

(8)

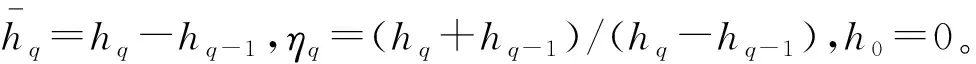
1.2 每层梁的位移函数

不计阻尼，采用分离变量法，则第q层梁自由振动的位移函数分量可以用下式表示：

uq(ξ,ζq,t)=Uq(ξ,ζq)ejωt，

wq(ξ,ζq,t)=Wq(ξ,ζq)ejωt

(9)

式中：t为时间，ω为裂纹梁的圆频率，j为单位虚数，Uq和Wq分别为第q层梁在x方向和z方向的振幅函数。

将式(9)代入式(6)和(7)中，可得一个振动周期内的第q层梁的最大应变能和最大动能分别为：

(10)

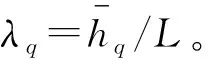
(11)

1.3 每层梁的振幅函数

利用第一类切比雪夫多项式和简单多项式的乘积分别构造x方向和z方向的振幅试函数：

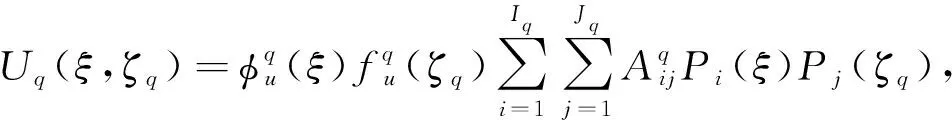
(12)

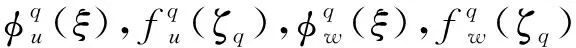
Ps(x)=cos[(s-1)arccos (x)],

s=1,2,3,…

(13)

本文两层梁的边界函数分量分别为

(14)

1.4 每层梁的特征方程

由瑞利-利兹法，得：

(15)

将式(10)～(14)代入式(15)可以得到第q层梁的特征值方程：

([Kq]-Ω2[Mq]){Xq}=0

(16)

式中 :

式中：[Kq]和[Mq]分别是第q层梁的刚度矩阵和质量矩阵，可以通过高斯数值积分得到；{Aq}，{Bq}是第q层梁特征值方程中未知系数组成的特征向量。

(17)

式中：

(18)

式中，

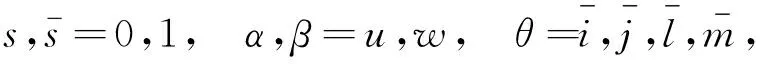
δ=i,j,l,m

(19)

1.5 裂纹梁的特征方程

根据式(16)，裂纹梁的特征值方程为

([K]-Ω2[M]){X}={0}

(20)

式中：

{X}={{X1} {X2}}T

由于上下两层梁在界面处须满足位移连续性条件，即：

U1(ξ,1)=U2(ξ,-1)，

W1(ξ,1)=W2(ξ,-1)

(21)

将式(21)代入式(12)得：

(22)

又由于切比雪夫多项式具有如下性质：

Pc(1)=1，Pc(-1)=(-1)c-1，

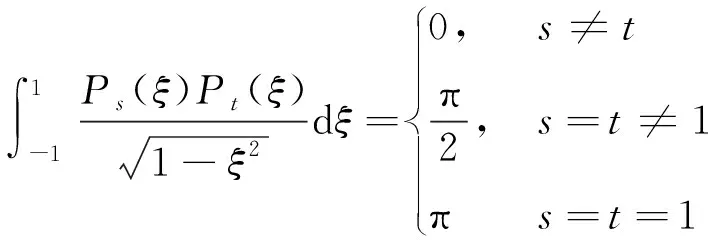
(23)

将式(23)代入式(22)，两边同时乘以PI(ξ) (I=1,2,3,…,I2)并在区间(-1,1)对(积分得式(24)。

l=2,3，…，L1

(24)

其中，

由于式(20)中的列向量{X}的系数并不都是独立的，须通过式(24)消去非独立系数，新建立一个含有N个独立系数的列向量。

(25)

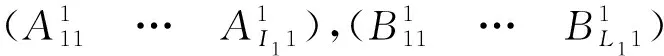
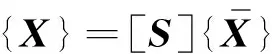
(26)

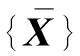
将式(26)代入式(20)得:

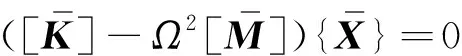
(27)

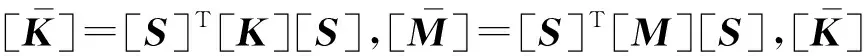
通过求解广义特征值方程(27)，可以得到任意阶无量纲特征频率和相应的特征模态系数。

2 特征频率的收敛性和比较研究

为了验证本方法的精确性,考察一端部带有裂缝的悬臂梁，计算参数为：h/L=0.1,v=0.3。为了便于分析，可对振幅函数U、W截断相同的切比雪夫级数项即：(I1=I2=L1=L2=m)和(J1=J2=M1=M2=n)。表1给出了不同裂缝深度(h1/h=0.1、0.2、0.5)下，裂纹梁前八阶无量纲频率参数Ω的收敛性。由表可知，随着截断项(m×n)的增加可以保证前八阶无量纲特征频率参数具有四位有效数字的精度。

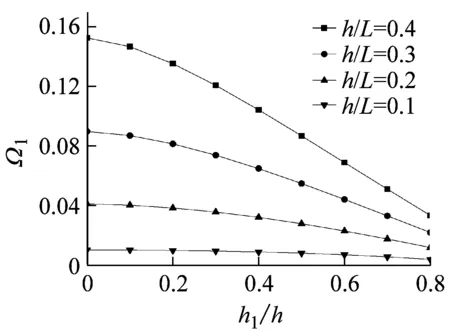
(a) 第一阶频率

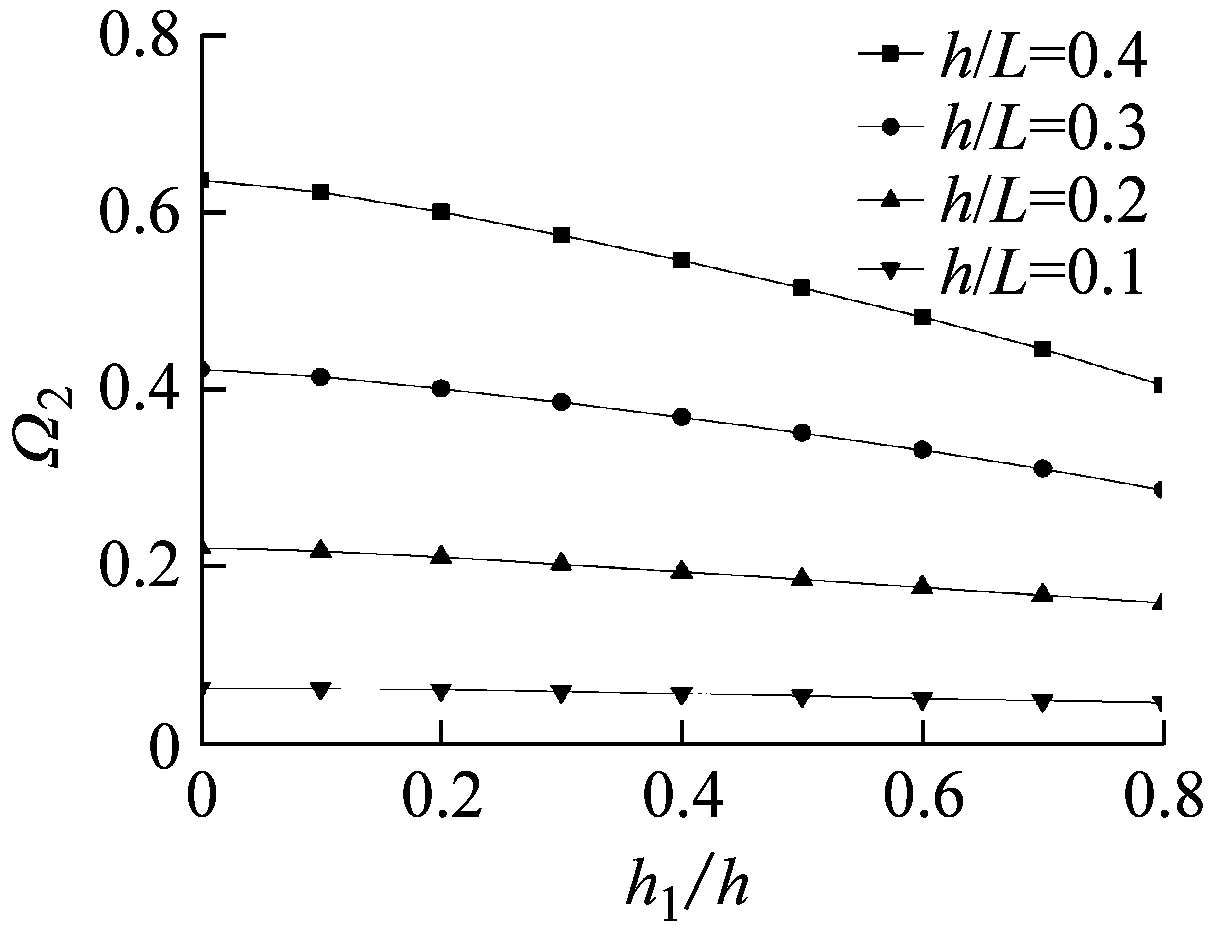
(b) 第二阶频率

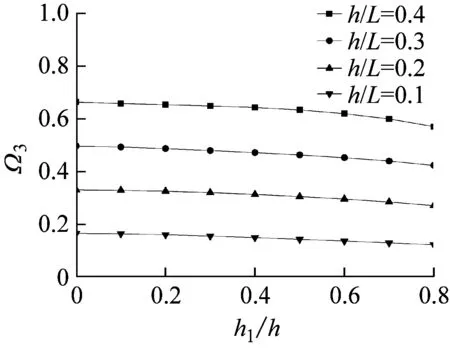
(c) 第三阶频率

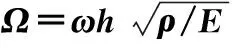
图2 不同高跨比下裂缝深度对前三阶无量纲频率的影响

表2给出了不同高跨比(h/L=0.1，0.2，0.3)下，裂纹梁的前八阶无量纲频率参数Ω与有限元解的比较。从表中可以看出，二者的结果吻合很好，其最大相对误差只有0.06%，证明本文分析方法对于含裂缝的细长梁和短粗梁都是有效的。

表3进一步给出了高跨比为h/L=1/15时，第一阶频率参数Ψ的本文解和文献[1]以及有限元解的比较。可以看出，对于浅裂纹，本文解和二者的结果都很接近，证明用本文方法研究此类问题的适用性与优越性。

3 参数分析

为了研究高跨比和裂缝深度对悬臂梁特征频率的影响。图2给出了不同高跨比(h/L=0.1，0.2，0.3，0.4)下，裂缝深度对前三阶无量纲特征频率的影响。由图2可知，随着裂缝深度的增加，频率逐渐减小，且频率的减小速率逐渐增大；随着高跨比的增加，裂缝深度对第一阶频率的影响将越来越明显。

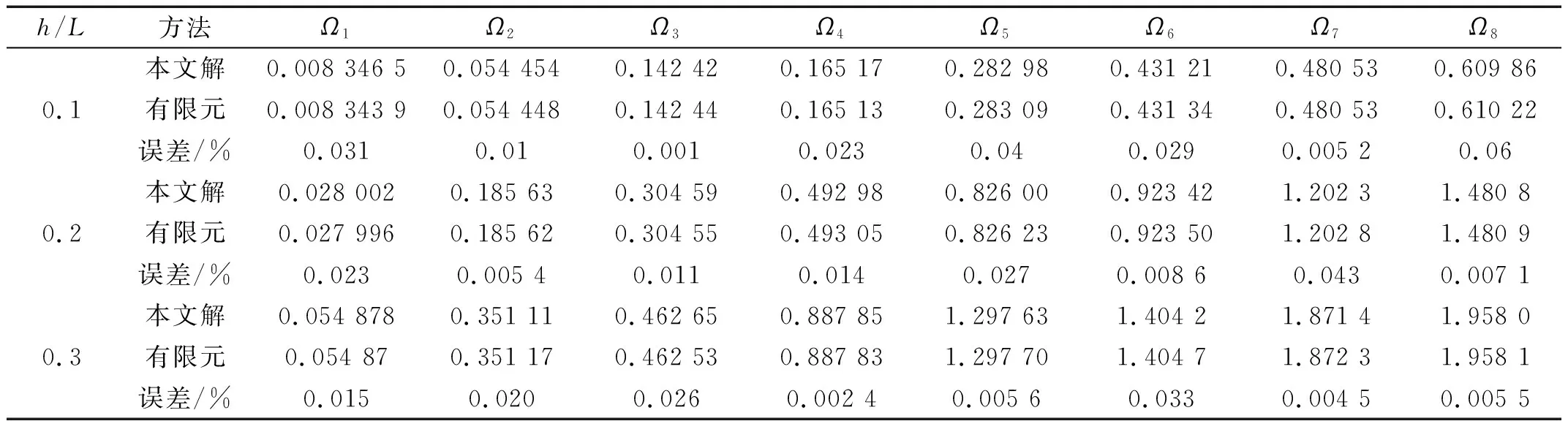
表2 有限元和本文结果的比较(h1/h=0.5)

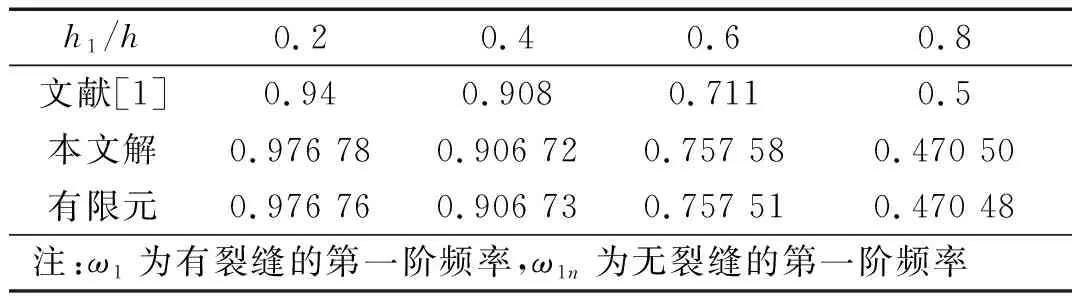
表3 第一阶频率参数Ψ=ω1/ω1n的比较

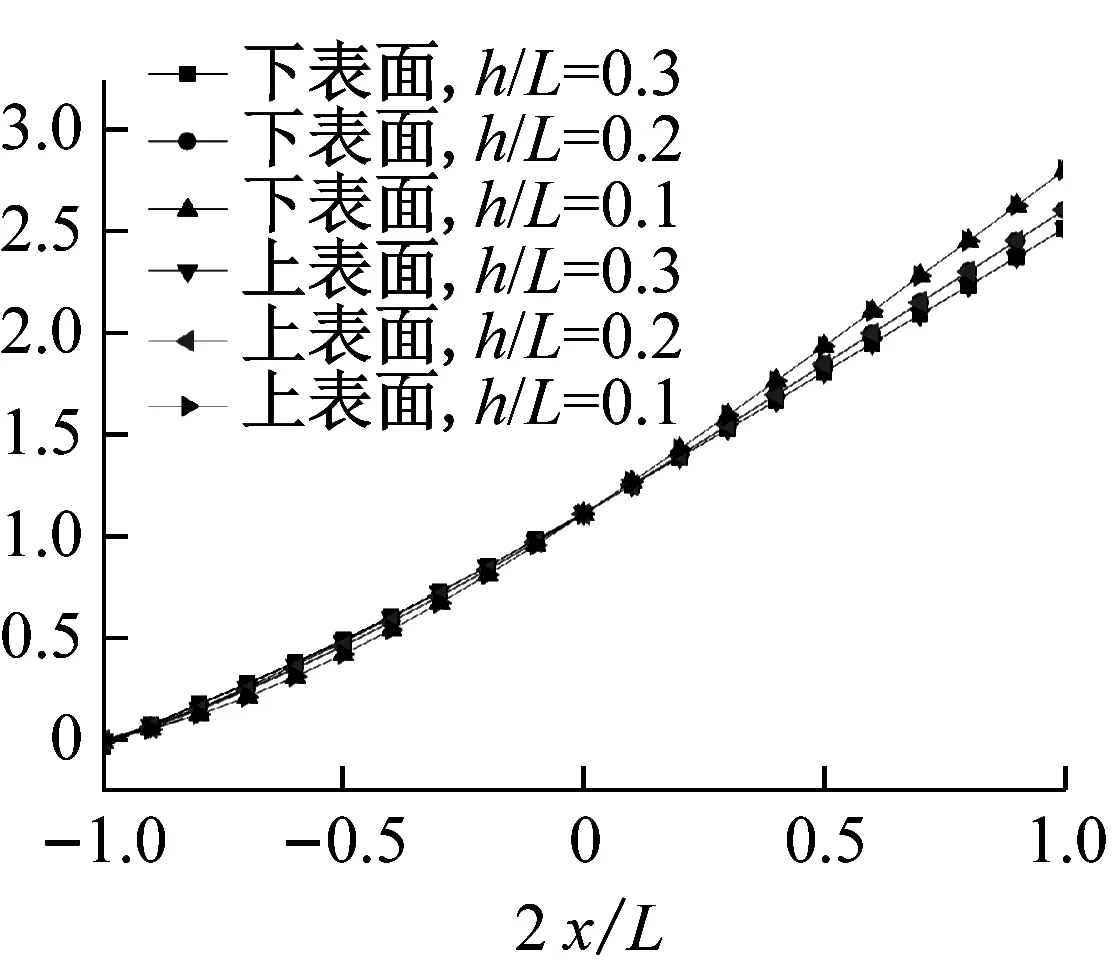
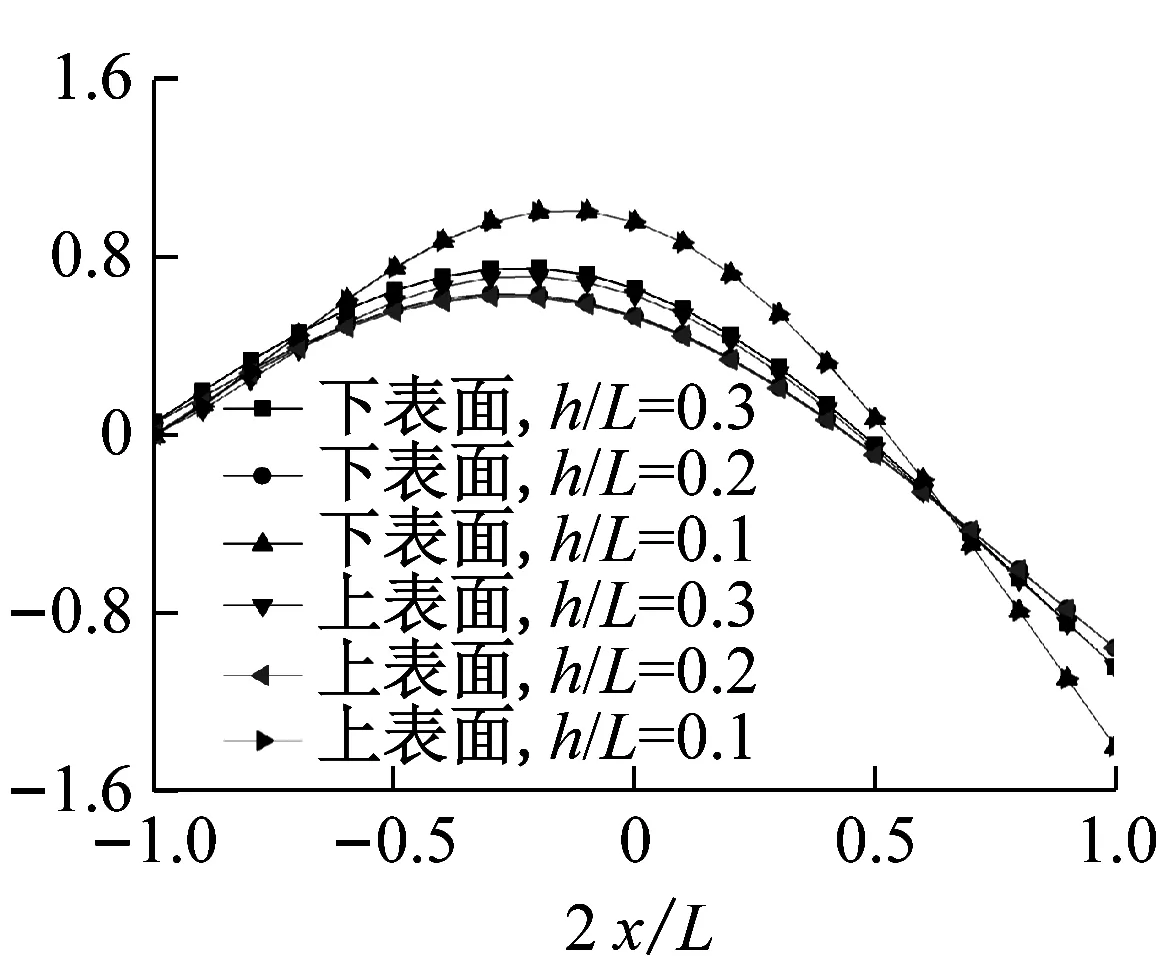
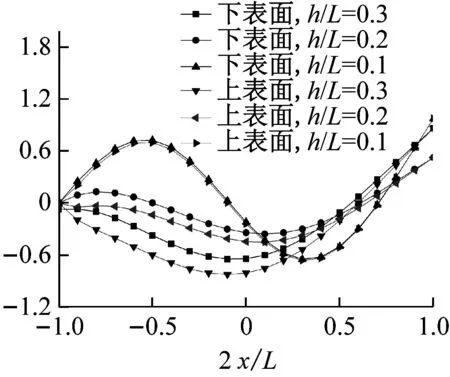
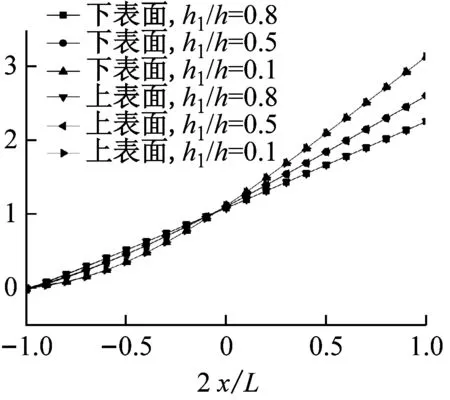
考察高跨比和裂缝深度对悬臂梁上下表面振型的影响。取h1/h=0.5，图3给出了不同高跨比(h1/L=0.1，0.2，0.3)下，梁上下表面竖向位移W的前三阶振型图。从图中可以看出，高跨比越大、频率阶次越高，梁的上下表面振型差异就越大。图4给出了高跨比为h/L=0.2时，不同裂缝深度(h1/h=0.1、0.5、0.8)下的悬臂梁上下表面竖向位移W的前三阶振型图。由图可知，频率阶次越高、裂缝越深，梁上下表面振型的差异就越大。

(a) 第一阶频率

(b) 第二阶频率

(c) 第三阶频率

图3 不同高跨比下W的前三阶振型图

Fig.3 The first three mode shapes ofWfor different height span ratios

(a) 第一阶频率

(b) 第二阶频率

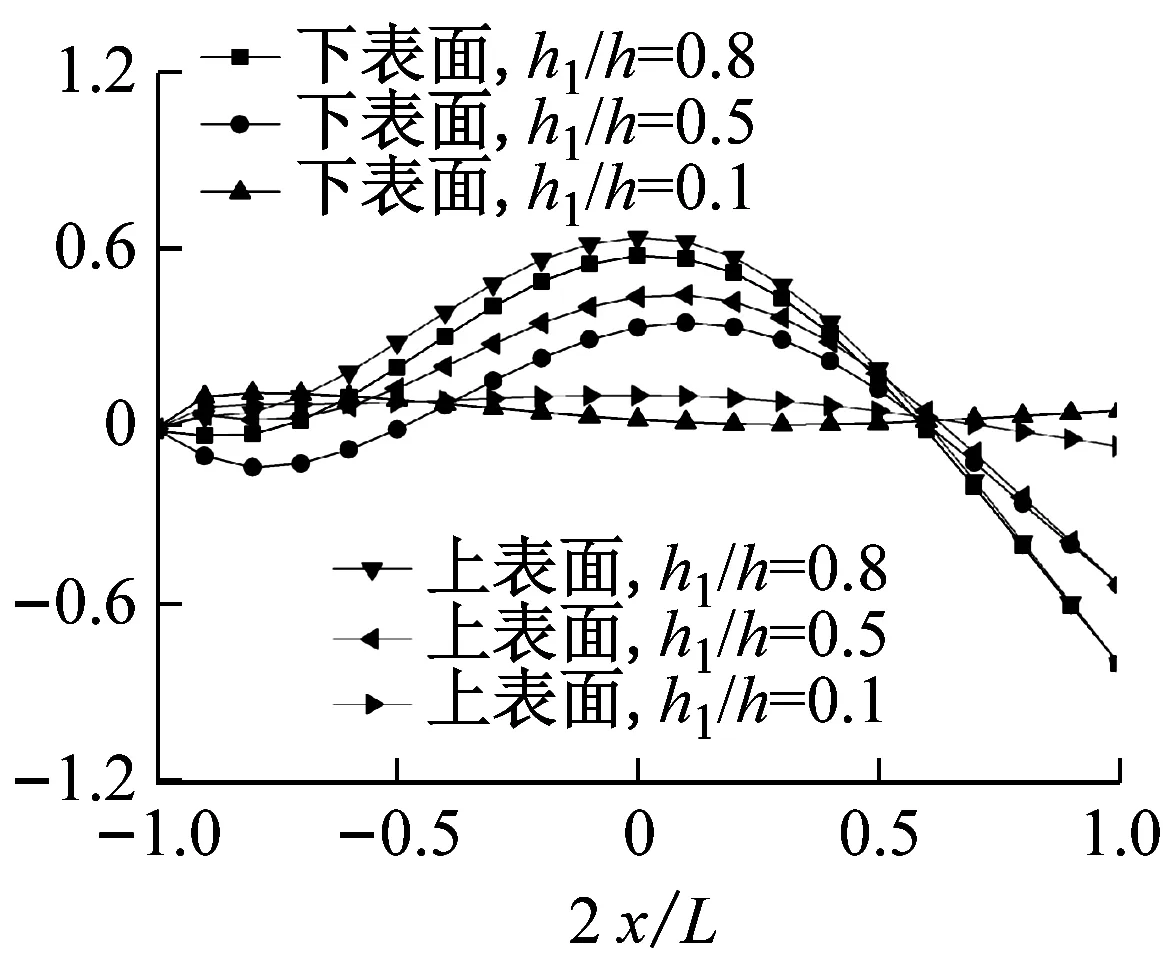
(c) 第三阶频率

图4 不同裂缝深度下W的前三阶振型图

Fig.4 The first three mode shapes ofWfor different crack depths

4 结 论

本文基于二维线弹性理论，利用切比雪夫-利兹法建立端部有裂纹悬臂梁的振动特征方程。将本文解与已有文献以及有限元解进行比较验证了本方法的正确性和精确性。参数化分析了裂缝深度、高跨比对特征频率和振型的影响。主要结论如下：

(1) 相比于文献中的等效弹簧法，本文求解特征频率无需任何模型假设。建立了一个简单和精确的端部裂纹梁分析模型。使用切比雪夫多项式与几何边界函数的乘积来构造梁位移试函数，数值结果显示出本方法收敛性好、精度高,可求得任意高跨比下裂纹梁的任意阶特征频率。

(2) 随着裂缝深度的增加，频率逐渐减小，裂缝越深，频率下降越快。高跨比越大，裂缝深度对基频的影响越大。

(3) 随着频率阶次的增加，裂缝深度和高跨比对梁上下表面竖向振型的影响越大。