基于大涡模拟的台北101大楼风致响应分析

卢春玲， 李中洋， 李秋胜

(1.桂林理工大学 土木与建筑工程学院，桂林 541004；2.桂林理工大学 广西有色金属隐伏矿床勘查及材料开发协同创新中心，桂林 541004； 3.广西岩土力学与工程重点实验室，桂林 541004； 4.香港城市大学 建筑系 香港 100013)

1 工程概况

超高层建筑具有质量轻、强度高、高宽比大且自然振动频率以及阻尼较低等特性。故对风力所造成的扰动较敏感，在风力作用下可能产生较大的风致响应。基于安全性与使用者的舒适性考虑，风力设计往往成为决定超高层建筑结构设计的重要因素。

台北101大楼地面以上101楼，地下5层。地面以上高度508 m，坐落在台北繁华地段信义计划区内。

大楼的立面图如图1所示，大楼造型宛若劲竹节节高升。平面为正方形，边长从46～64 m不等。大楼采用双层结构，外层由8根巨大的钢柱组成，在大楼的四个外侧分设两根。巨型柱的最大截面长3 m、宽2.4 m，自地下5楼贯通至地上90楼，柱内灌入高密度混凝土，外以钢板包覆。地震力和风力作用时，这些巨型柱提高大楼的横向刚度。内层结构为大楼提供可用空间。大楼每隔8到10层设置钢桁架组成的转换层。图2给出了桁架转换层的位置。

图1 台北101大楼立面图

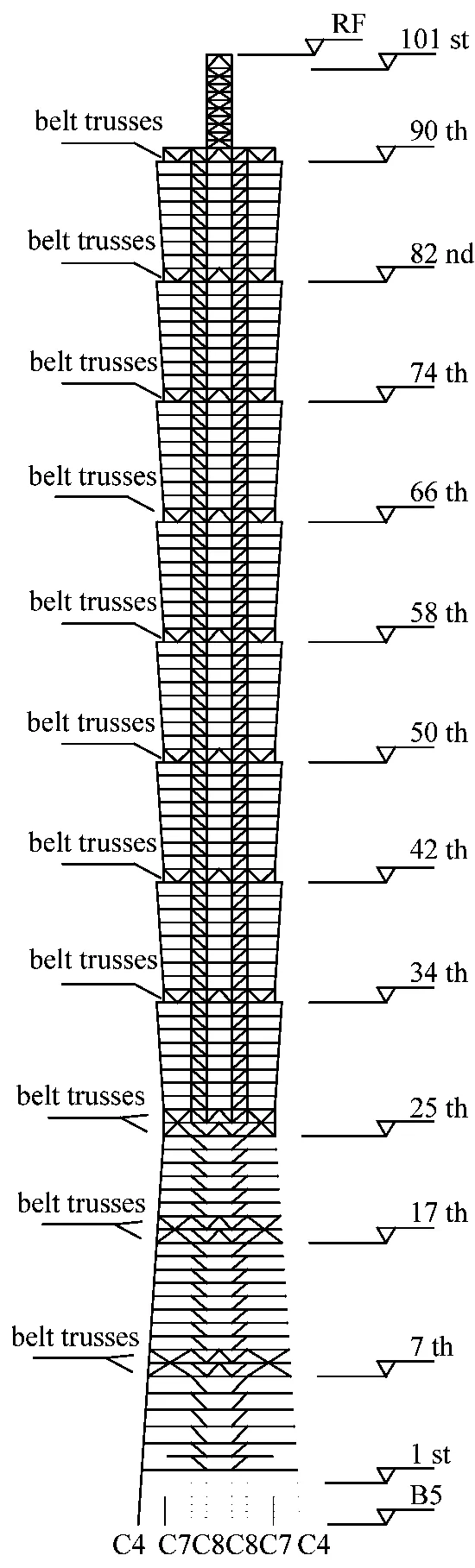
图2 台北101大楼结构体系立面图

为了降低大楼受高空强风及台风作用造成的摇晃，大楼内设置了单摆式TMD(Tuned Mass Damper, TMD)系统，即调频质量阻尼器。它由数块钢板堆叠焊接而成。钢球直径为5.5 m，总重约为660 t，钢球底下设置8根液流阻尼器，以提供TMD系统额外的消能机制，以降低钢球晃动行程。质块阻尼器利用钢索悬吊，并由其调整钟摆的摆长(TMD悬吊于92楼至88楼)，使其自振频率与结构的基本频率一致而达到吸收结构振动能量的功能。阻尼器的设置详见图3。

台北101大楼属风敏感建筑。同时台北市又位于世界上台风多发的区域，台风可能使得101大楼承受远远大于普通高层建筑承受的荷载。这些特点使得该建筑需要对台风作用下大楼的结构性能进行深入细致的研究。

(a)总体图(b)详细构造图

图3 台北101大楼阻尼器布置图

Fig.3 Damper layout of Taipei 101 Tower

大涡模拟(LES)是现今计算风工程的研究热点之一。随着数值模拟技术和计算机性能的提升，研究人员尝试将大涡模拟运用到工程实践中。例如，顾明[1-3]、李秋胜[4-5]、周志勇[6]等采用LES对结构风效应进行了分析[7-9]。利用大涡模拟进行实际超高层建筑中进行结构风荷载及响应研究还较少[10]。本文应用大涡模拟并结合一种新的可满足大气边界层中风场特性的湍流脉动速度生成方法——离散再合成的随机湍流生成法(DSRFG)[11]模拟非稳态边界层湍流风场。在大涡模拟的亚格子模型方面，采用一种新亚格子模型[12]，基于Linux系统下Fluent软件，模拟得到台北101大楼周围的风流场及作用于其上的风荷载时程数据。建立大楼的3维有限元计算模型，计算出风荷载作用下大楼的风致响应以及等效静力风荷载。并将计算结果与现场实测以及风洞试验的相应数据进行对比，以对该数值模拟方法的实用性和准确性进行检验。

2 大楼强振监控系统概况

安装在台北101大楼上的强振监测系统主要由传感器和数据采集处理系统两部分组成。传感器系统包含30个加速度传感器，分别安装在大楼的-5th (地下室)，1 st，36 th，60 th，89 th和101 st层，如图4所示。为测得大楼的扭转加速度，部分加速度传感器设置在所在层的中心为对称点的两个不同位置，如图5所示。通过分析和处理传感器测得的数据，可获得大楼的加速度响应以及动力特性，如自振频率、模态以及阻尼比等数据。

本文用于对比分析的现场实测数据是由采样频率为200 Hz的数据采集系统从2005年8月到2008年5月期间，三次台风作用和一次地震作用下采集得到。

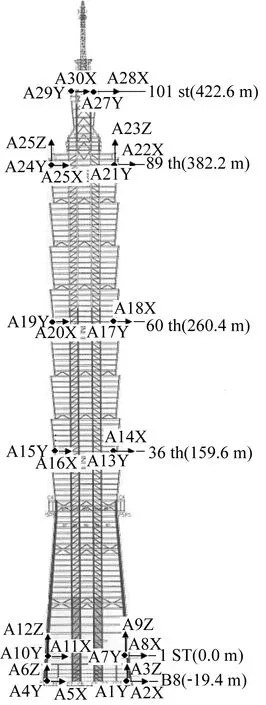
图4 加速度传感器立面布置图

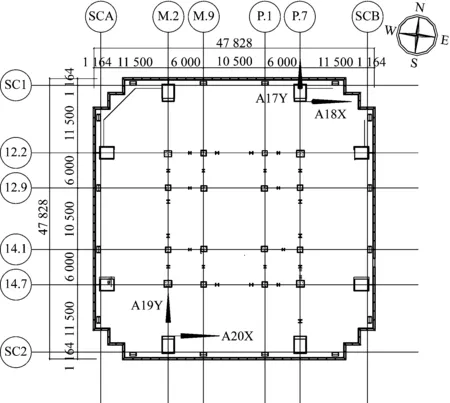
图5 加速度传感器平面布置图

3 大楼大涡模拟

3.1 模型建立与网格划分

台北101大楼的计算模型为全尺寸，数值模拟的计算模型以及计算域如图6所示，X方向长为23 Db(Db为建筑的宽度)，Y方向宽为16 Db，Z方向高度为两倍的建筑高度。计算域中建筑物的阻塞比小于3%。

网格的划分情况如图7所示，对建筑物周围网格进行局部加密，为了提高网格质量，这部分网格采用四面体网格。在加密区域以外采用了六面体网格。总的网格数量为320万左右。建筑模型表面采用5层棱柱体网格，第一层壁面网格的高度选取为0.01 m，最大网格歪斜度(skewness of equisize angle)为0.89，网格尺寸增长率取为1.05。近墙壁y+值约为35～85，适用于壁面函数。

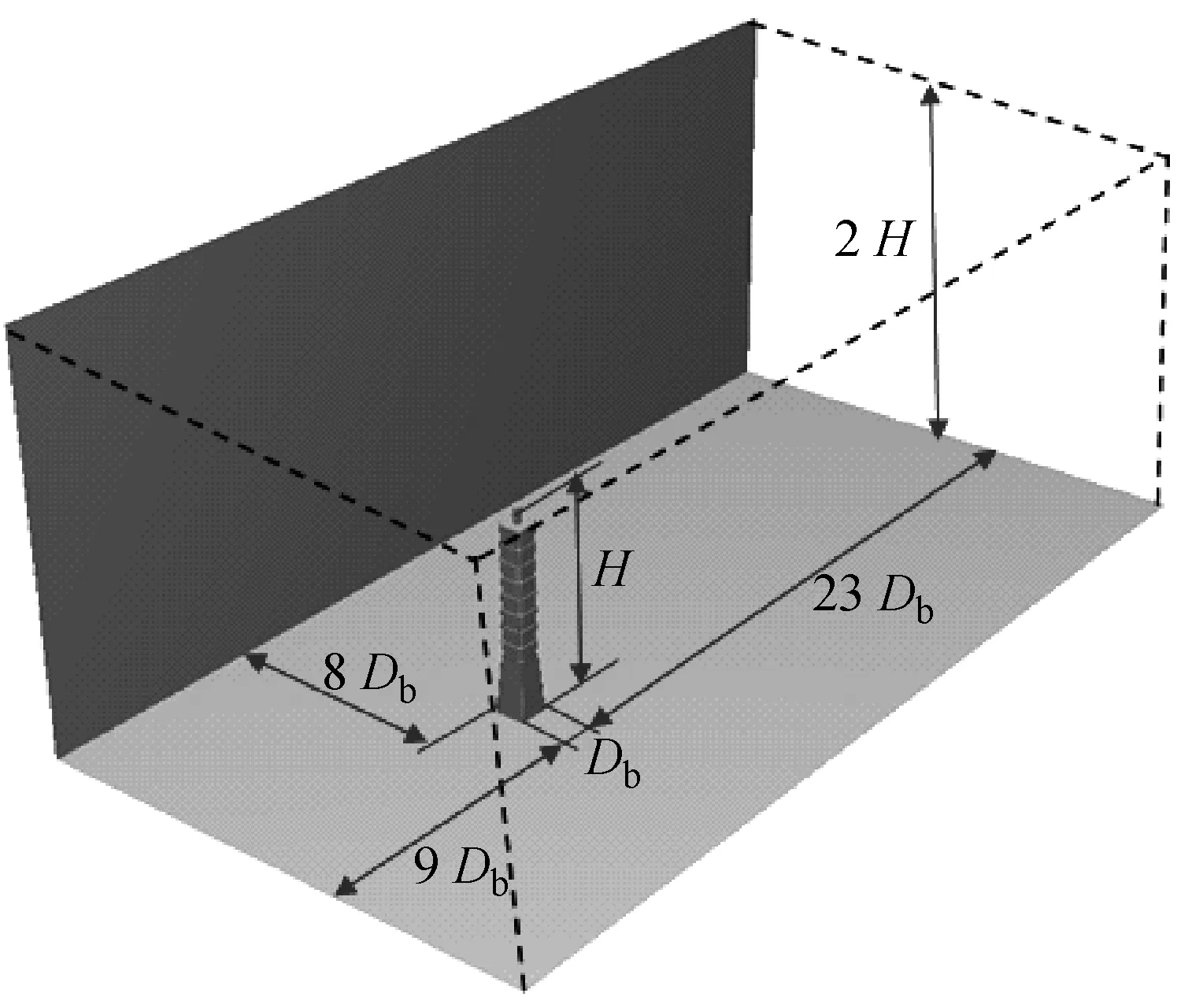
图6 台北101大楼计算模型及计算域

图7 台北101大楼计算模型及计算域

3.2 边界条件的设定

本文大涡模拟采用作者提出的一种新的湍流入口生成方法-DSRF方法[11]。此方法在综合了以往方法优势的基础上，具备的优点包括：①严格保证入口湍流满足连续性条件div(u)=0；②基于严格的理论推导，具有通用性。生成的脉动速度满足指定的谱密度函数；③入口湍流的空间相关性可通过相关性尺度因子调整；④每个坐标点的入口湍流生成过程相互独立，适用于并行计算。⑤能处理输入湍流功率谱及湍流积分尺度的各向异性。速度入口处平均风速沿高度的变化服从指数率，见式(1)。

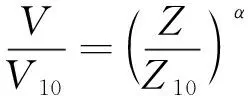
(1)

式中：Z10和V10为10 m高度和10 m高度处的风速。基于台北松山机场气象站测量的近地风速观测数据采用风气候统计模型得到50年回归期的十分钟平均风速V10为每秒43.27 m/s，α=0.15，Z为高度变量。

本文基于Shiau[13]在台湾基隆港的观测塔测(距离台北北部约20 km)得的26 m高度处的强风(台风)数据的结果：纵向湍流积分强度在0.18～0.23之间，纵向湍流积分尺度在40～200 m之间，对应的风速为27～45 m/s。以及李秋胜等[14-15]在强风作用时，现场实测得到香港中环大厦(374 m)以及深圳定王大厦(384 m)楼顶处的风场数据结果：湍流强度在0.1～0.4之间，湍流积分尺度在171～600 m之间，风速在5～25 m/s。基于以上的现场实测数据，确定了台北101大楼入口处的湍流强度剖面及湍流积分尺度的分布，如图8所示。采用DSRFG方法生成的入口处的瞬时风速分布图如图9所示。通过DSRFG方法生成的入口处脉动风速时程的功率谱与目标谱卡曼谱的比较如图10所示。由图10可知，大涡模拟所生成的脉动风速时程功率谱与目标谱一致，故其功率谱特性符合大气边界层湍流的要求。

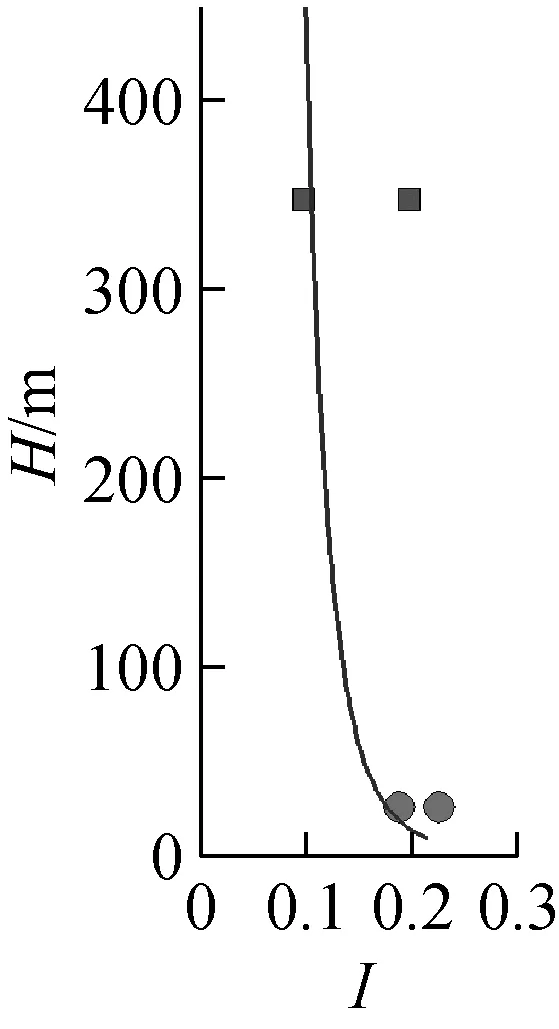
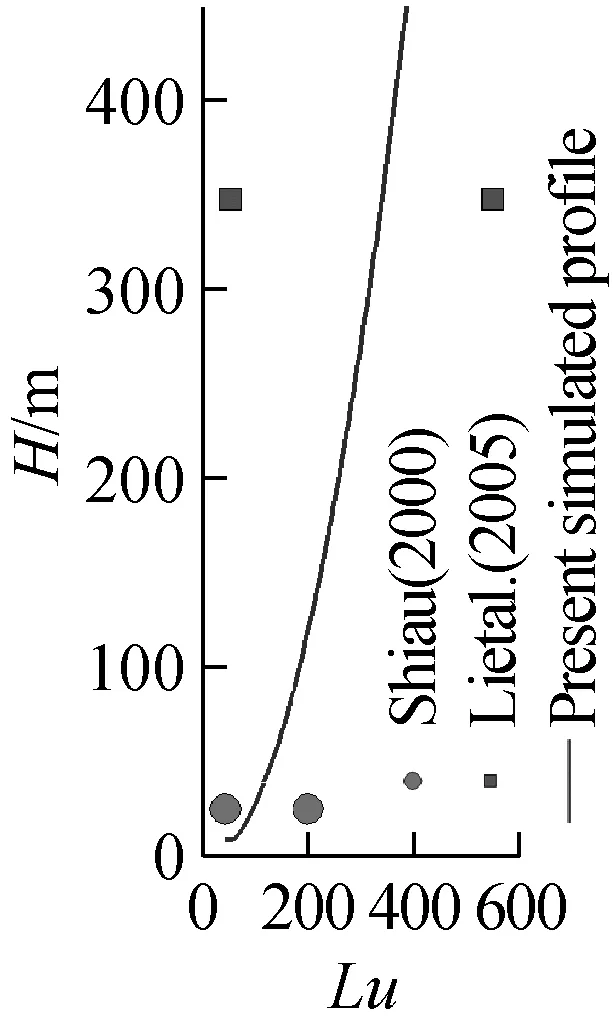
图8 入口湍流强度及积分尺度剖面

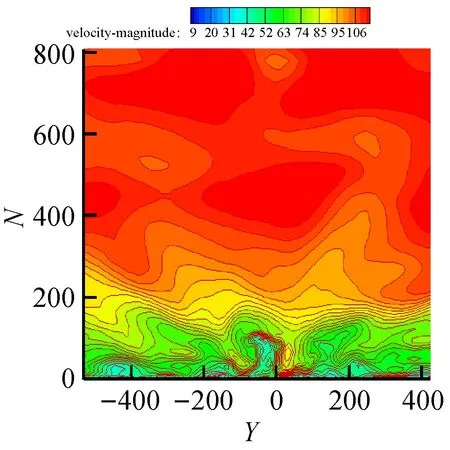
图9 DSRFG方法产生的入口瞬时风速场

Fig.9 Instantaneous velocity field at the inflow boundary generated by the DSRFG method

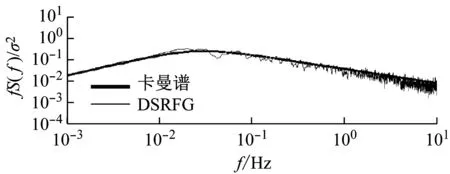
图10 DSRFG方法生成的脉动风速时程功率谱与目标谱比较

Fig.10 Velocity sequence spectrum generated by DSRFG and comparison with the target spectrum

流场的出口认为湍流完全发展，流场变量散度为零。计算域顶部与两侧为自由滑移壁面，壁面剪应力为零。建筑表面和地面采用无滑移的壁面条件限定流体和固体区域。

3.3 大涡模拟亚格子模型及计算求解

本文采用的大涡模拟新的亚格子模型的详细介绍参见文献[12]。新亚格子模型的主要特点是：适合工程应用、一方程模型、不需采用试验滤波, 适合低阶格式及无结构网格应用，具有动态特征，且计算量少。

在数值求解中，认为空气的流动是不可压缩的。数值计算采用压力隐式分割算法(PressureImplicit with Splitting of Operators, PISO)进行迭代求解。时间离散采用二阶隐式格式，空间离散采用二阶中心格式。为了使得计算更快的收敛，在大涡模拟计算之前先进行了RANS模型的计算，将RANS模型计算的结果通过瞬态化处理作为大涡模拟计算的初始流场。考虑到大涡模拟计算的准确性及计算时间成本，大涡模拟非定常计算的时间步长取为0.05 s。共进行了16 000步的大涡模拟非定常计算。流场数据的统计计算采用了最后11 000步的计算结果。

本文的计算在32CPUs并联成的高性能计算机集群上进行。LES的计算开销如下：内存使用12 GB，计算总耗时达733 h，每个时间步长耗时约60 s。速度和压力收敛残差标准选取为10-5。

4 大涡模拟计算结果与分析

4.1 流场

由于风洞试验受到试验条件和手段的限制，很难测得建筑物周围的整个流场的情况，CFD方法则不受此限制，可以给出非常完整的结果。如风速分布和风速矢量图等，为设计提供参考。

大涡模拟得到的台北101大楼周围的平均、瞬时以及根方差风流场如图11(a)～(c)所示。从图中可以看出，典型钝体扰流的流场特点，如在建筑物迎风前方以及两侧的流动分离、涡旋脱落、尾流等都得到真实的再现。从图11(b)可以看出，在建筑物前方有大量的随机涡旋结构。不同频率的风速脉动与分离区域中的涡旋结构相互作用，产生密集的涡旋脱落，这也是高层建筑横风向脉动风力产生的主要原因。

根方差风速代表了风速脉动大小，从图11(c)中可以看出，建筑物前方的根方差风速较小，其主要由来流湍流产生。在来流遇到建筑物的阻挡后，由于建筑物对流场的扰动，产生特征湍流，较大的根方差风速主要出现在流动分离区域以及涡旋脱落的尾流区域。

4.2 风荷载

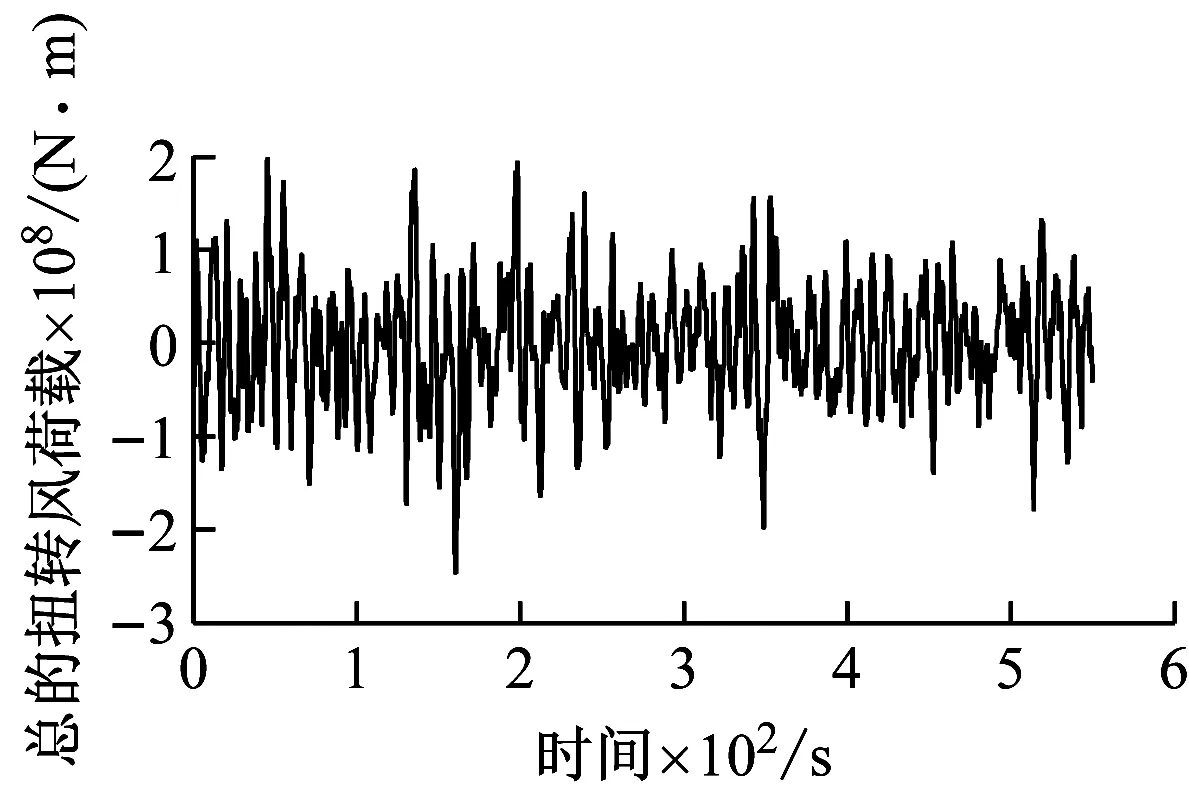
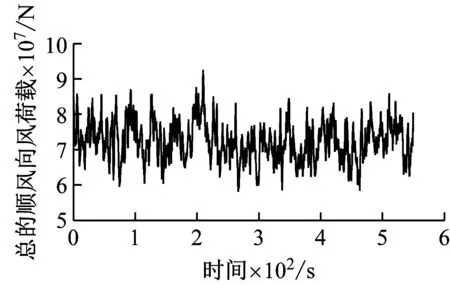
将台北101大楼分51层(基本两个楼层为一层)，通过积分得到这51层处大楼两个主轴方向上的风荷载Fx，Fy以及绕Z轴的扭矩的时程数据。通过对51层处的风荷载数据进行积分还可得到大楼总的风荷载。台北101大楼总的顺风向、横风向以及扭矩风荷载时程曲线见图12。从图12可看出风荷载的脉动是无序的，这说明数值风洞模拟预测出了作用在大楼上的随机风力。

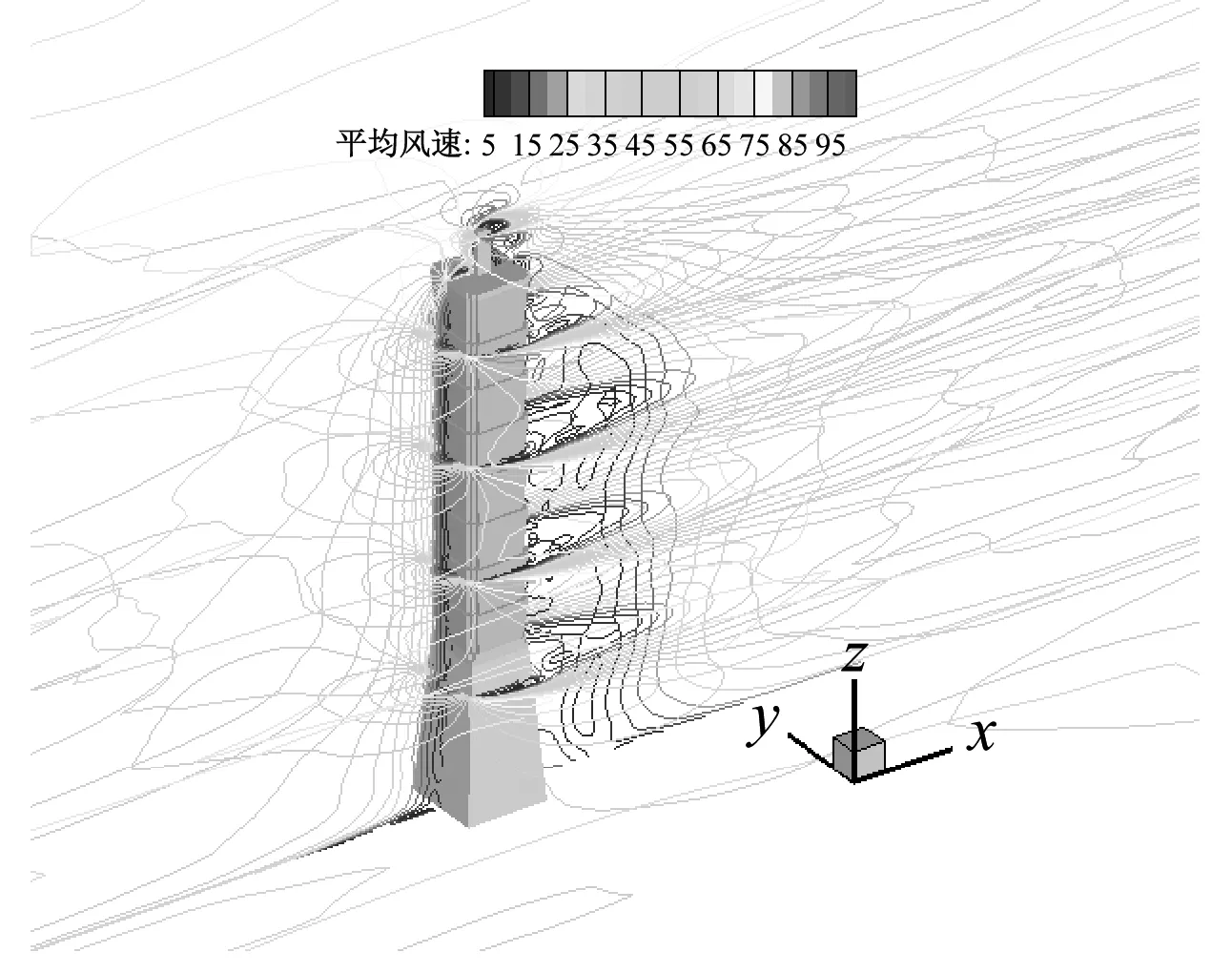
(a)平均风速流场

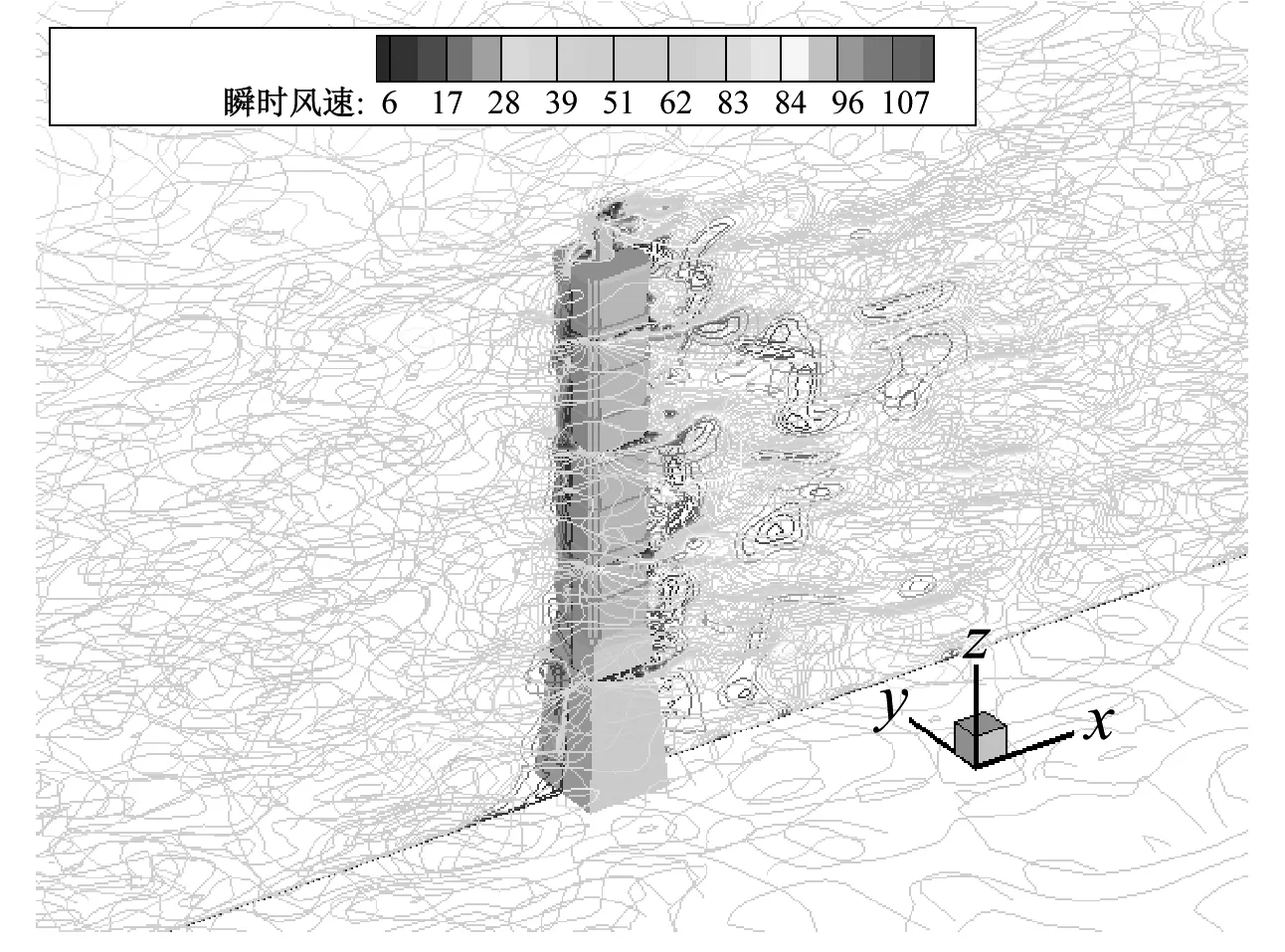
(b)瞬时风速流场

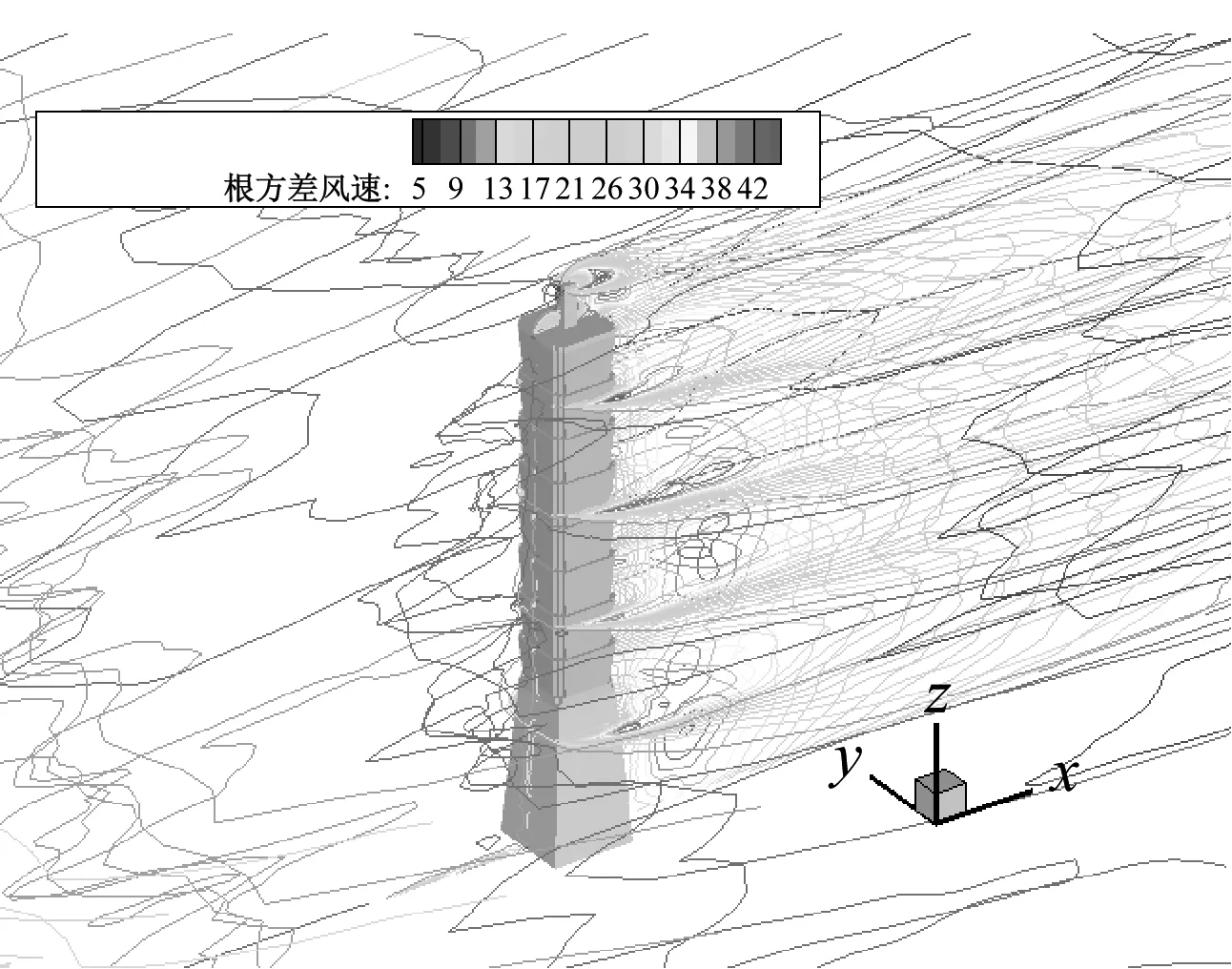
(c)根方差风速流场

图11 台北101大楼周围风速流场

Fig.11 Instantaneous velocity contours around Taipei 101 Tower

(a)顺风向风荷载

(b)横风向风荷载

(c)扭转向风荷载

图12 台北101大楼总的风荷载时程曲线

Fig.12 Time-history of the wind forces

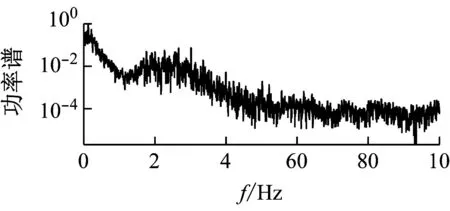
台北101大楼总的风荷载的功率谱以及2008年3月12日“汶川”地震作用下大楼实测得到的基底加速度功率谱如图13及14所示。对比图13和图14发现：大楼总的风荷载的功率谱能量与远场地震波导致的楼底的加速度的能量都主要集中在0～2 Hz频段。造成这一特殊现象的原因可能是地震波的高频部分在远距离(约1 890 km)的地层传输过程中被过滤掉了。这一现象也说明远场地震波对大楼的激励在一定程度上跟风荷载对大楼的激励相类似。

(a)顺风向风荷载

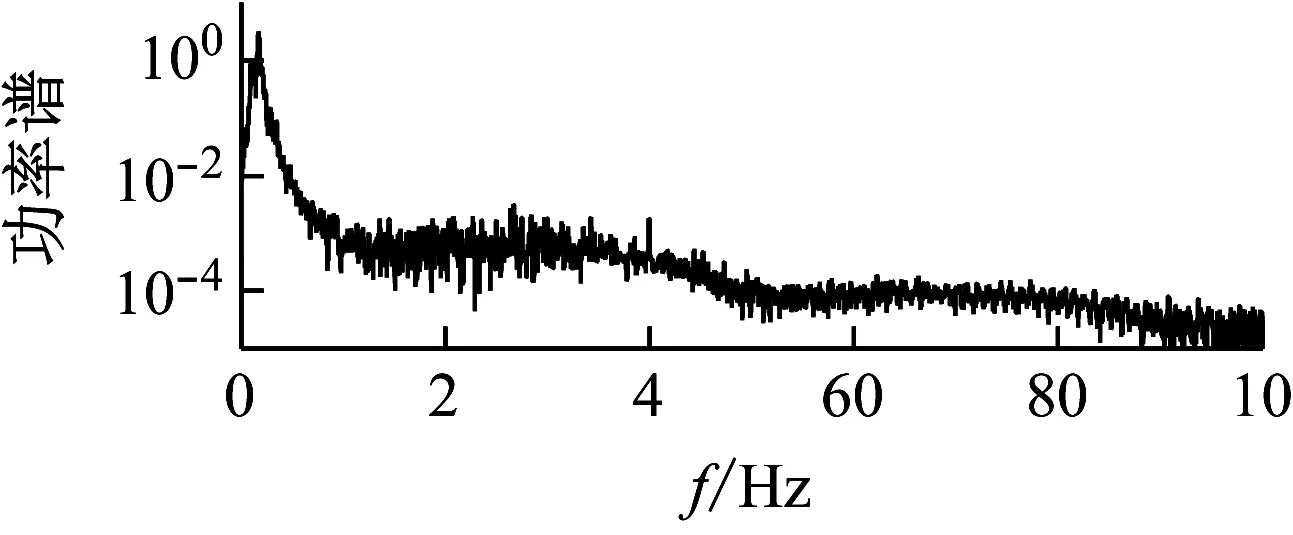
(b)横风向风荷载

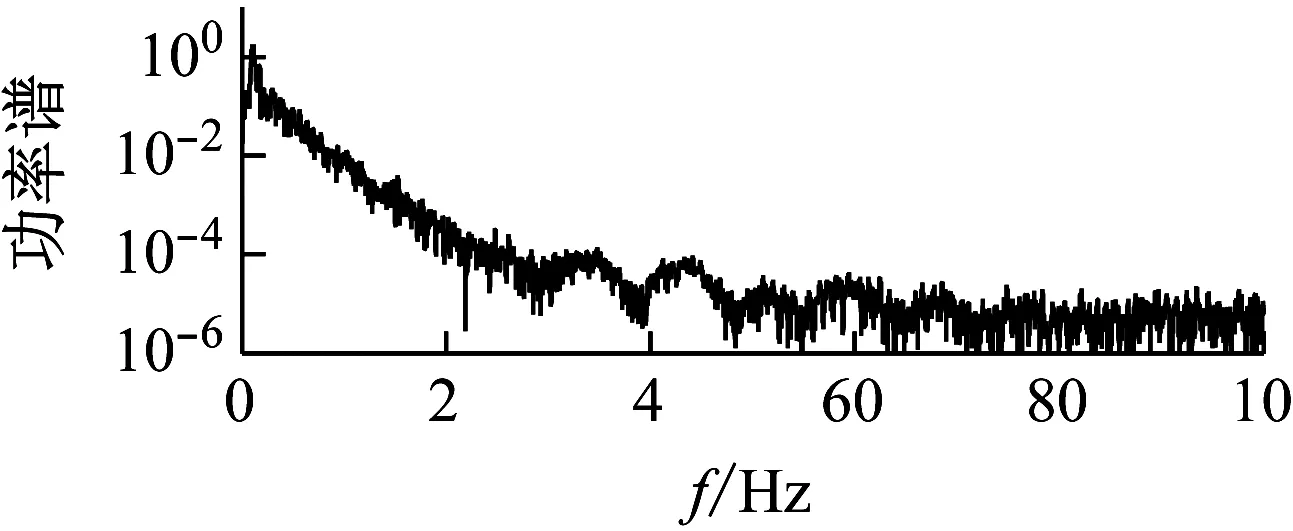
(c)扭转向风荷载

图13 台北101大楼总的风荷载功率谱

Fig.13 Power spectral densities of the overall wind forces

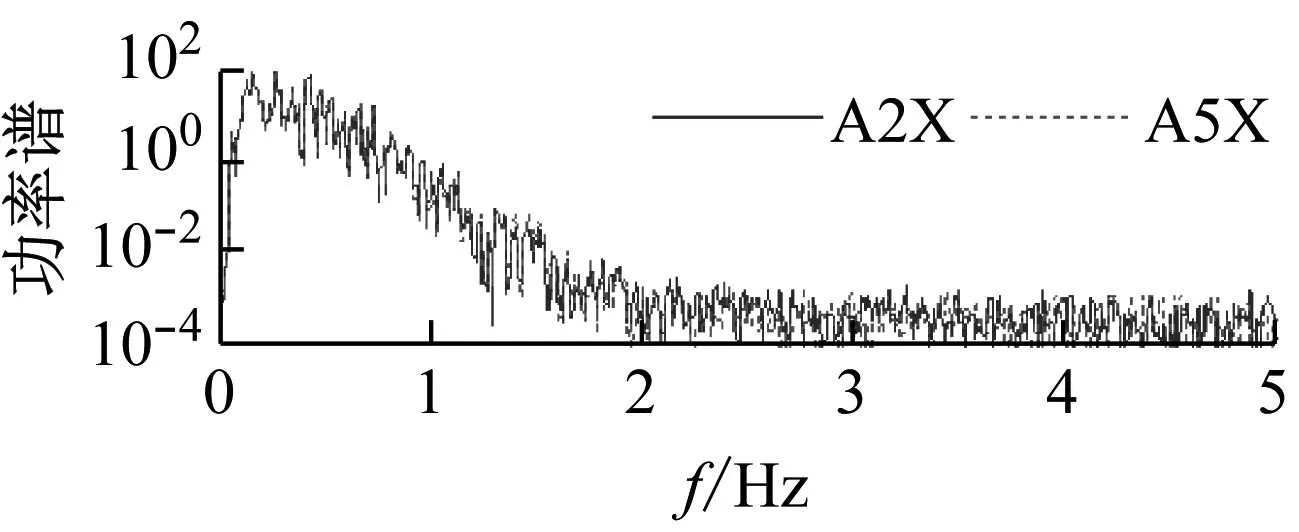
图14 “汶川”地震作用下台北101大楼基底加速度功率谱

Fig.14 Power spectral densities of the accelerations at the basement (B5) during Wenchuan earthquake

大楼在50层、40层、30层以及20层处积分得到的顺风向和横风向以及扭转的风荷载的功率谱分别如图15～17所示。

从图15中看出：顺风向风荷载的功率谱与典型的顺风向风荷载功率谱类似，能量集中在较宽的频带范围。不同层上的顺风向风荷载功率谱的峰值随着楼层的增高而下降，也就是低层的顺风向风荷载功率谱的最大能量高于高层的。这可能是由于气流在建筑的迎风面驻点以下下沉至地面形成回流，这一区域的湍流较大所造成的。除了功率谱峰值频段，不同层上的风荷载功率谱大小沿楼高没有明显的变化。

从图16表示的各层上横风向风荷载功率谱曲线来看，每条功率谱曲线都存在一个明显的尖峰，这可能是涡旋脱离产生的。这也说明横风向风荷载主要是涡旋脱落引起的。不同层上横风向功率谱的峰值沿建筑高度没有明显的变化。然而，在较高频段，各条功率谱曲线随着层高增加而抬高。这一现象的合理解释为：在较高的楼层，3维流动效应以及较高的风速在大楼侧墙上产生了较之低处较高的风压脉动。这也是横风向风荷载功率谱中高频部分能量的主要产生原因。

大楼各层上的扭矩功率谱如图17所示，在各条功率谱曲线上也都有一个明显的峰值，这一峰值所对应的频率也跟横风向荷载功率谱的峰值频率比较接近，这说明由来流风湍流和涡旋脱落导致的不平衡的脉动风压是产生扭矩的重要原因。

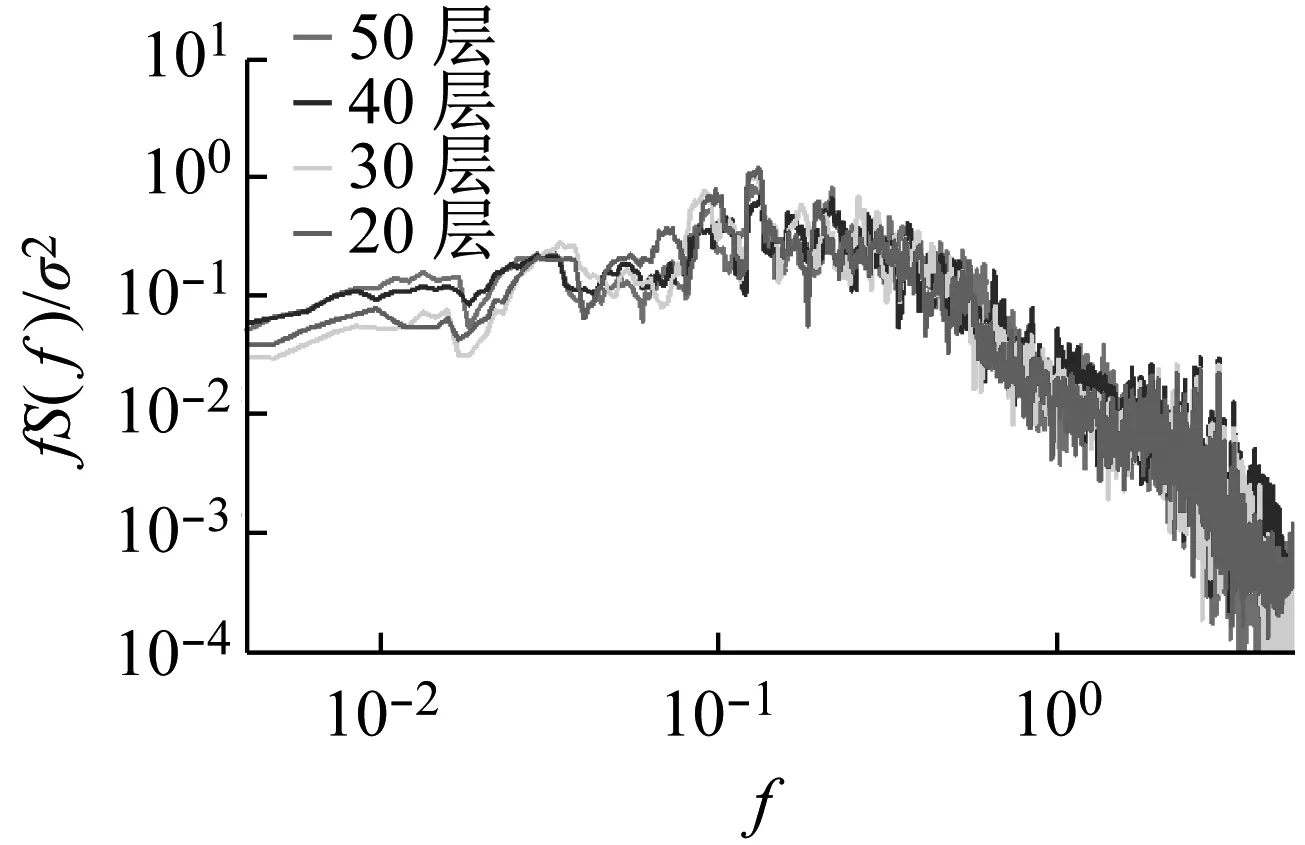
图15 台北101大楼总的顺风向风荷载功率谱

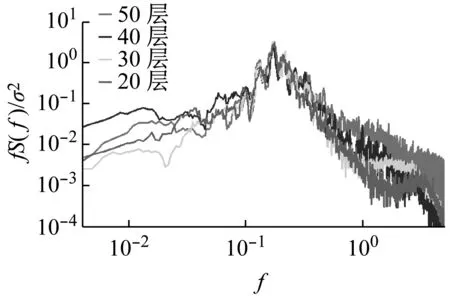
图16 台北101大楼总的横风向风荷载功率谱

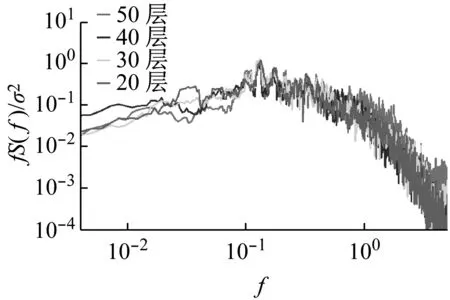
图17 台北101大楼总的扭转风荷载功率谱

5 风致响应分析

5.1 大楼三维有限元模型

台北101大楼的三维有限元模型如图18所示。在建立有限元模型时采用了4类单元：3维梁单元模拟柱和梁。3维杆单元模拟钢支撑。楼板用板单元进行模拟。活载以及其他非结构部分采用3维质量单元模拟。大楼在基础处的约束为3向固定约束。大楼的三维有限元模型共计20 532个梁单元，24 048个板单元, 以及3 496个杆单元。

5.2 模态分析

将有限元模型模态分析计算的大楼X和Y方向前三阶以及第一阶扭转自振频率与台风“马莎”、“泰利”、“柯罗莎”及“汶川”地震作用时台北101大楼现场实测数据得出的自振频率的平均值进行对比，结果列于表1中。从表1中可看出：有限元计算的自振频率与实测结果相差在5.9%～14%之间。这表明可利用有限元模型对大楼的风致响应进行分析。

基于有限元模型根据模态分析得到的台北101大楼前3阶X和Y方向自振频率对应的振型以及第一阶扭转自振频率对应的振型(相对于重心轴)如图19所示。

图20以及图21给出了台北101大楼由有限元模型计算出的以及通过3次台风以及“汶川”地震时由实测加速度数据得到的前三阶X、Y方向的振型(取大楼第101楼层的振幅为1)。从图中可看出有限元分析得到的振型与现场实测的结果基本一致。

图18 有限元模型

5.3 位移和加速度响应

通过ANSYS有限元瞬态动力分析得到的顺风向(X轴方向)以及横风向(Y轴方向)台北101大楼最高的居住层(第89层)中心处的位移以及加速度响应的时程序列如图22～23所示。

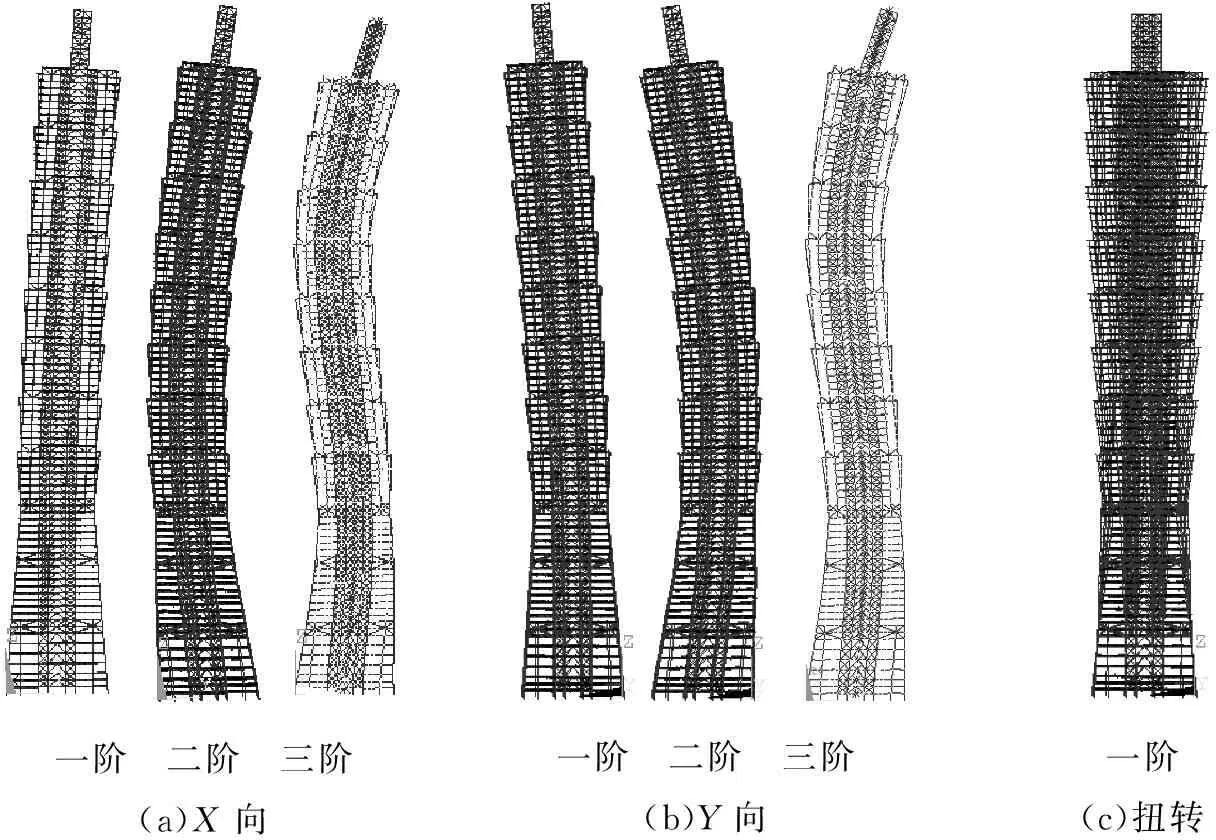
一阶 二阶 三阶(a)X向一阶 二阶 三阶(b)Y向一阶(c)扭转

图19 台北101大楼计算模态

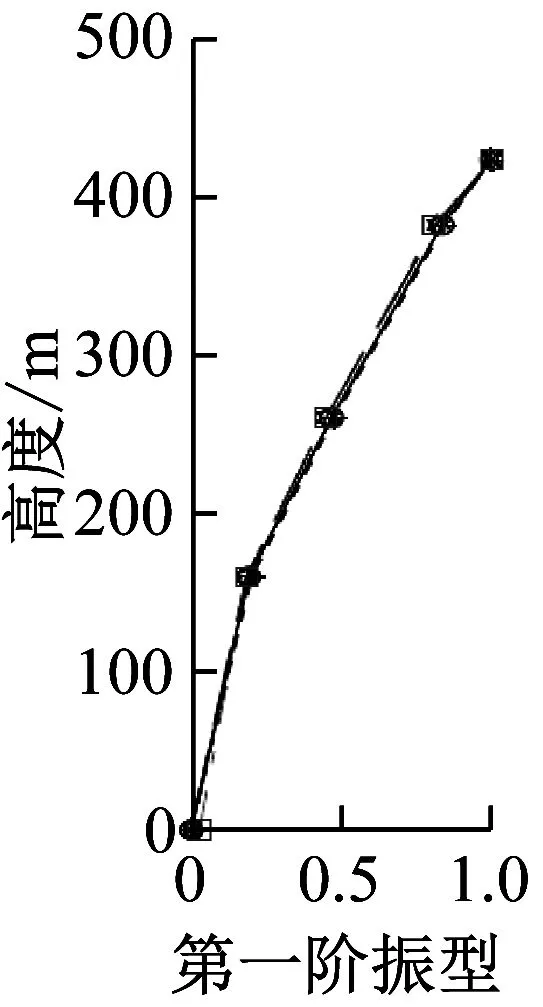
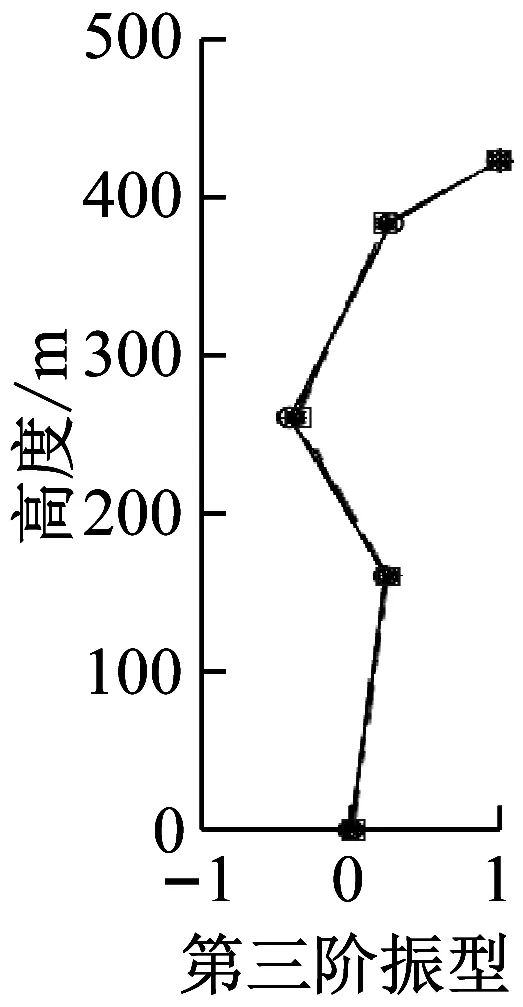
(a)3次台风和“汶川”地震中实测X向振型

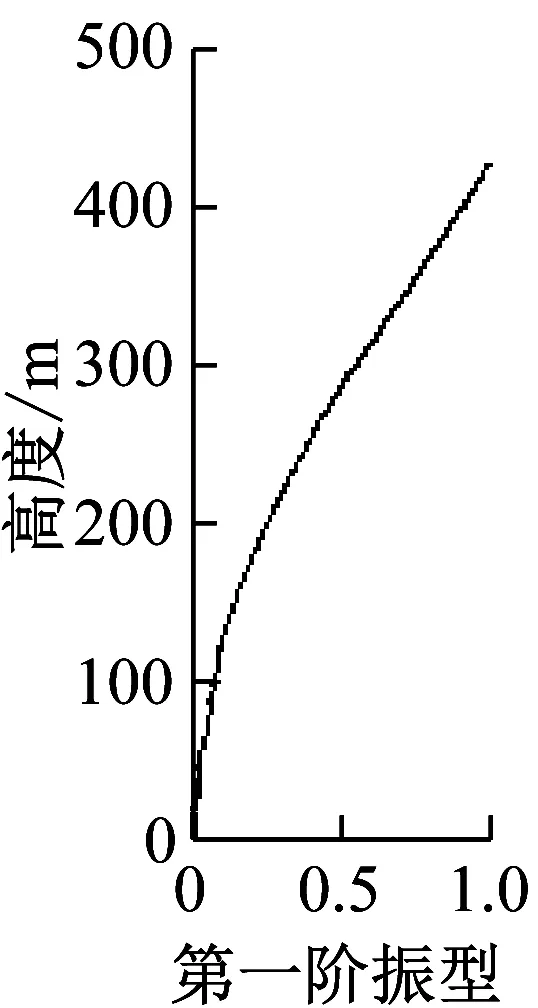
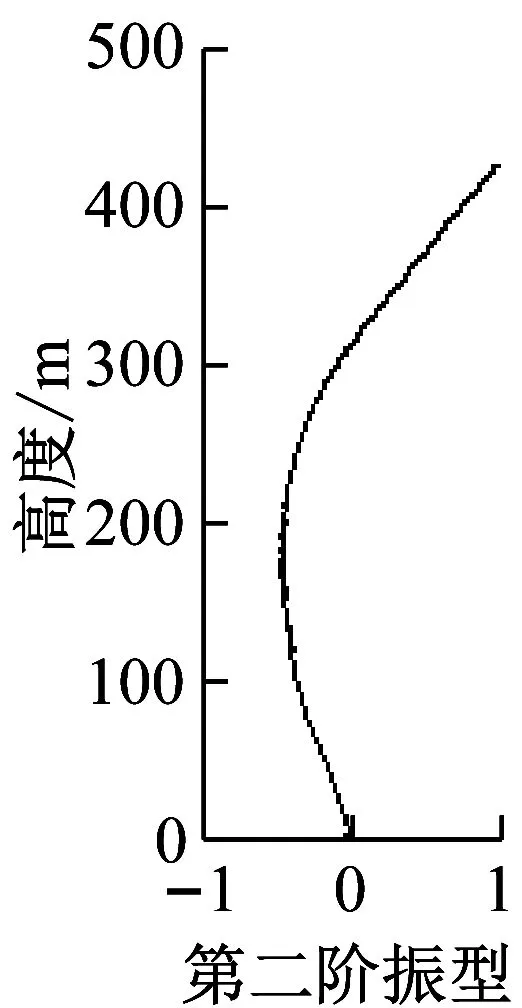
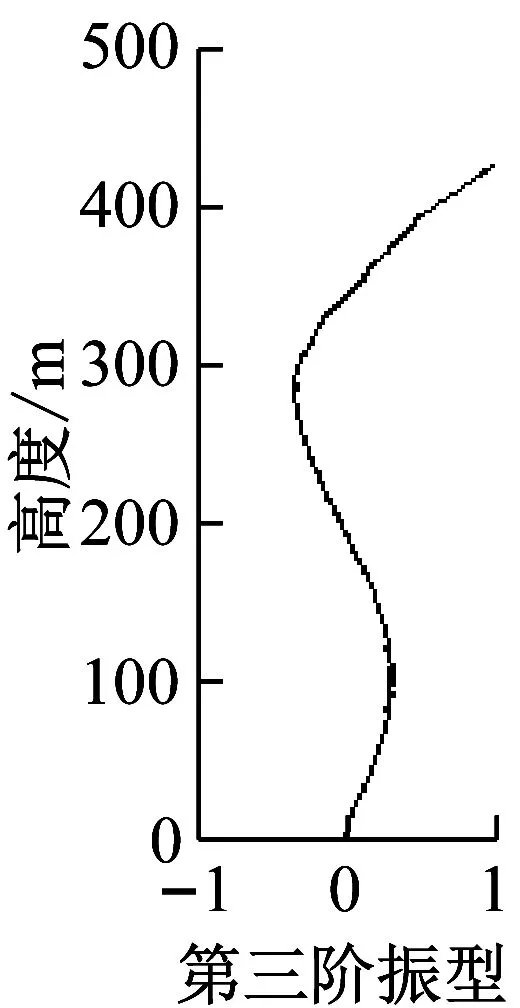
(b)有限元计算的X向振型

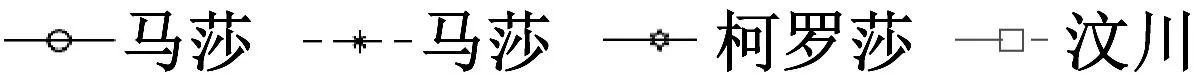
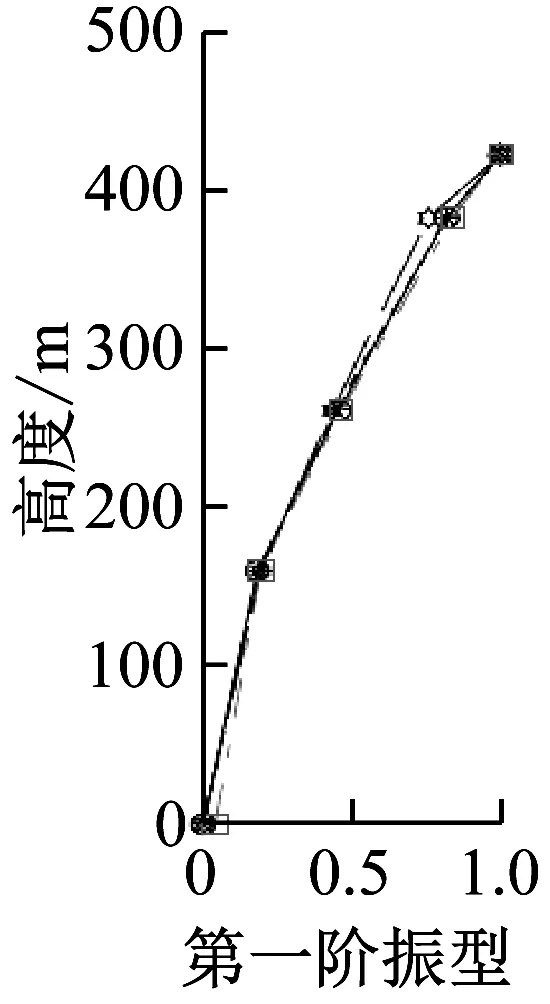
(a)3次台风和“汶川”地震中实测X向振型

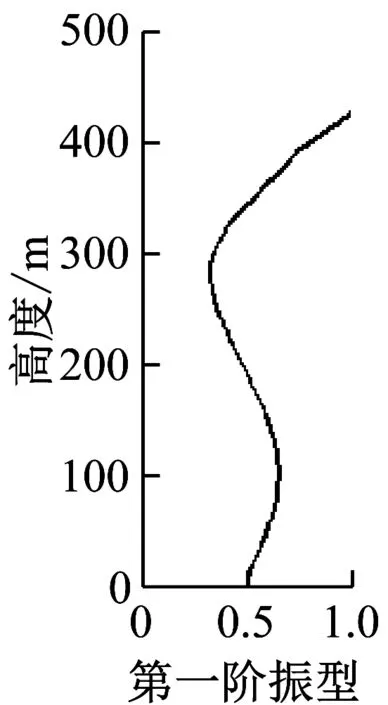
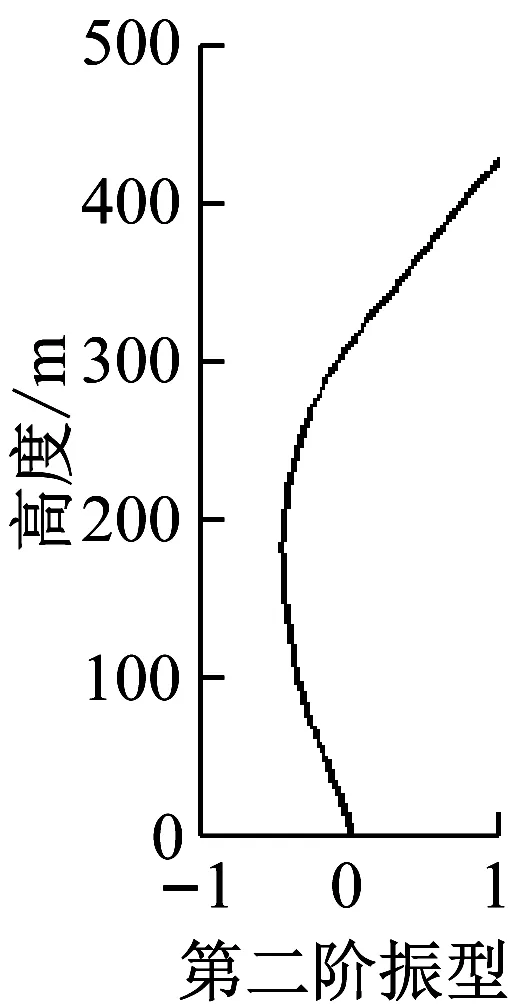
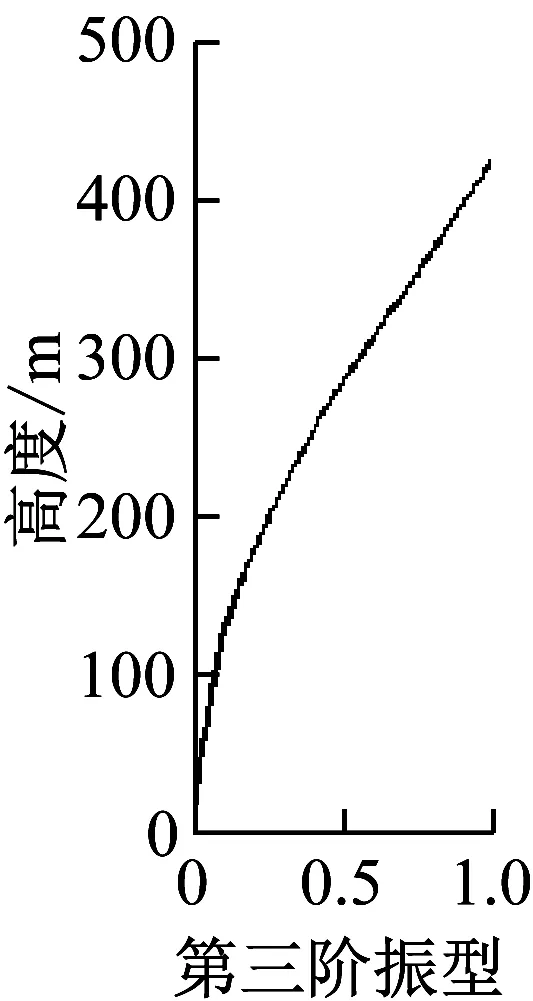
(b)有限元计算的X向振型

风荷载作用下，台北101大楼每层楼中心处X及Y轴方向上的位移以及加速度响应如图24～25所示。从图中可以看出：①大楼风致响应曲线较光滑，没有明显的拐点，其曲线形状类似于均布力作用下悬臂梁的变形曲线。②横风向的最大以及根方差位移以及加速度响应值均大于顺风向的结果。这也说明台北101大楼的横风向响应起主导作用。因此，在大楼的抗风设计中应该考虑横风向的响应以及风荷载。

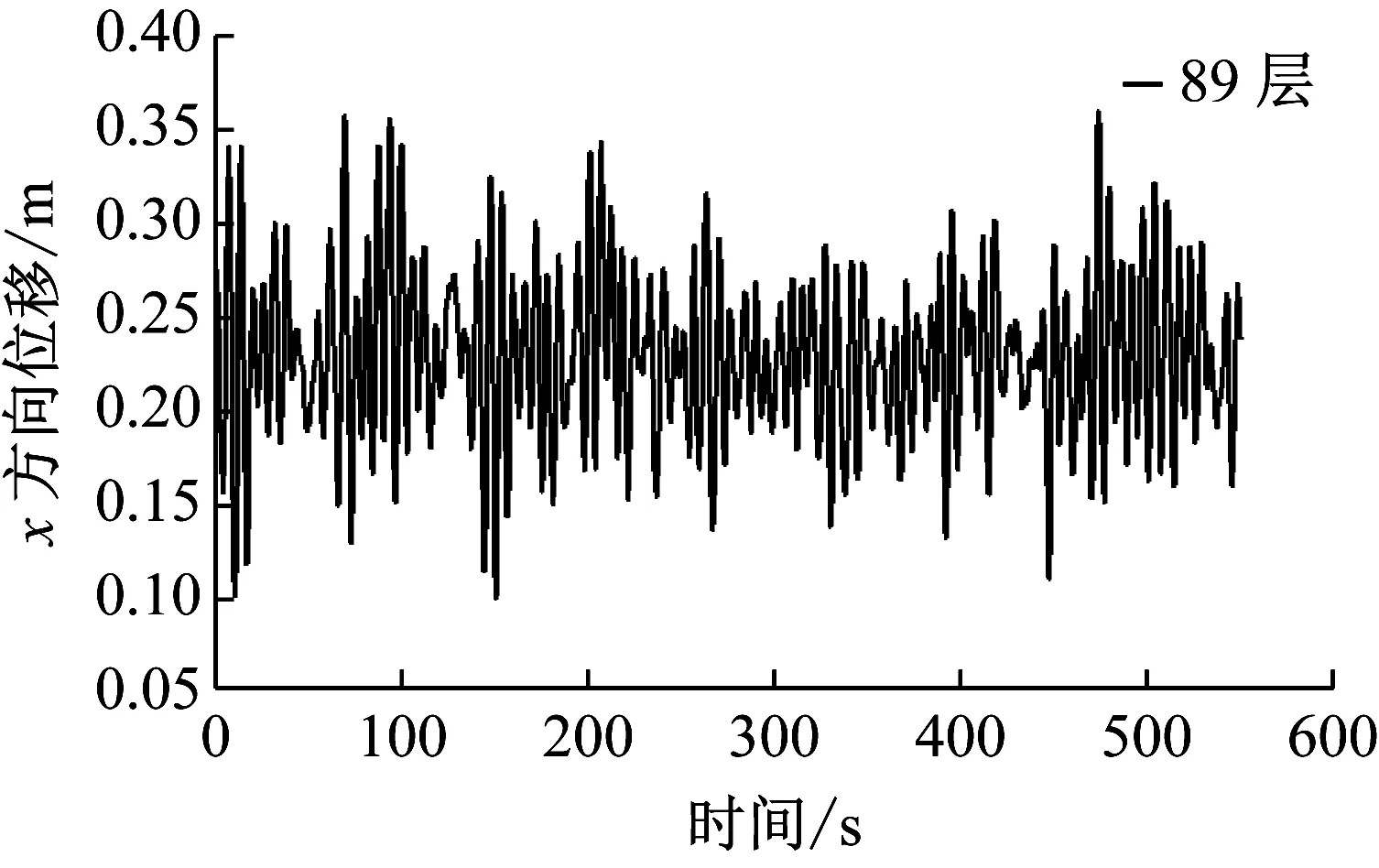
(a)顺风向

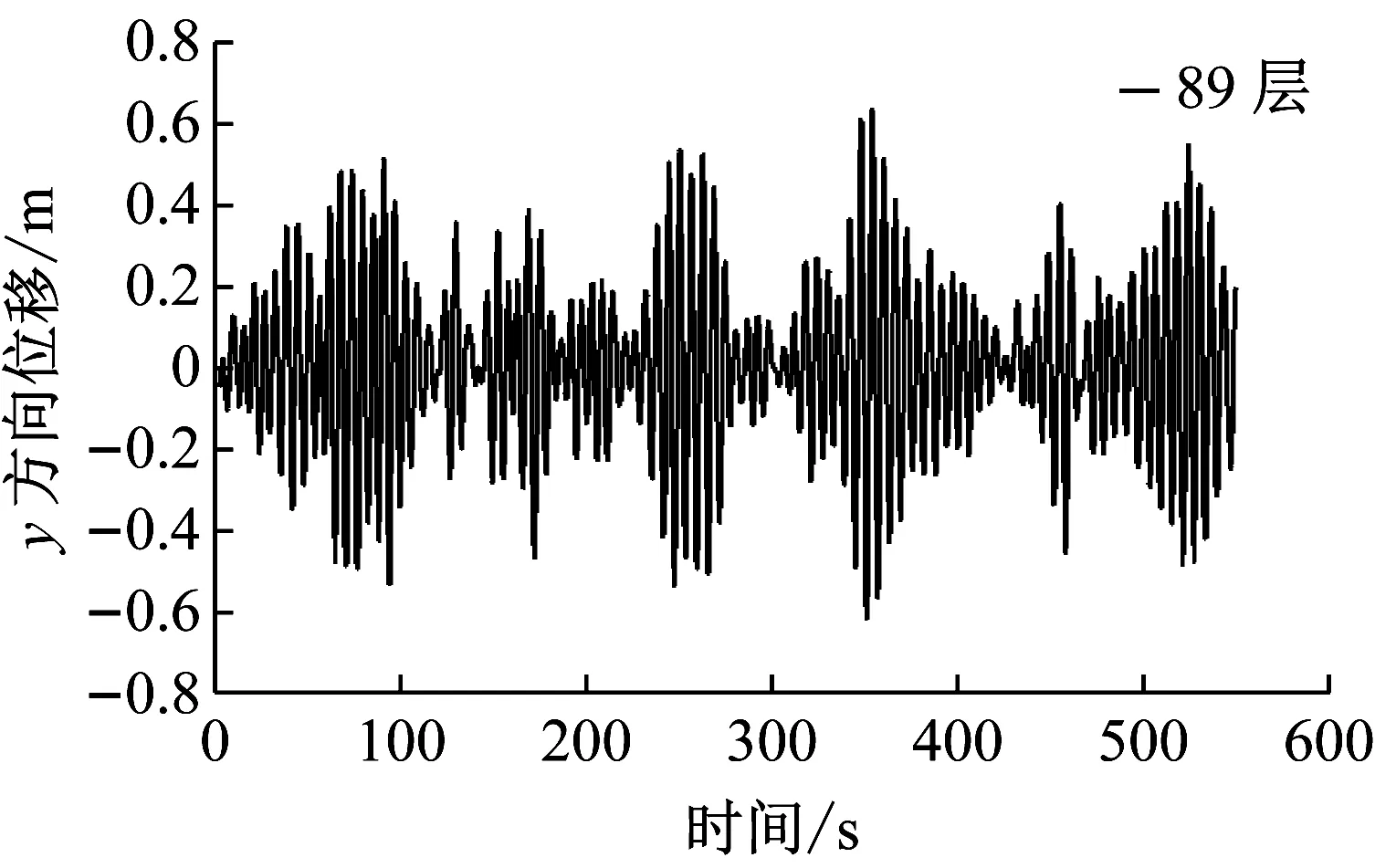
(b)横风向

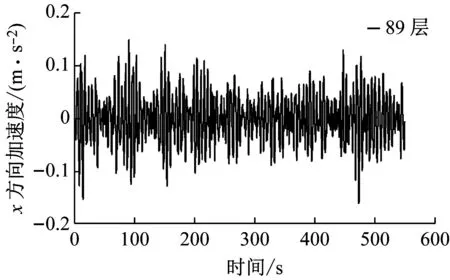
(a)顺风向

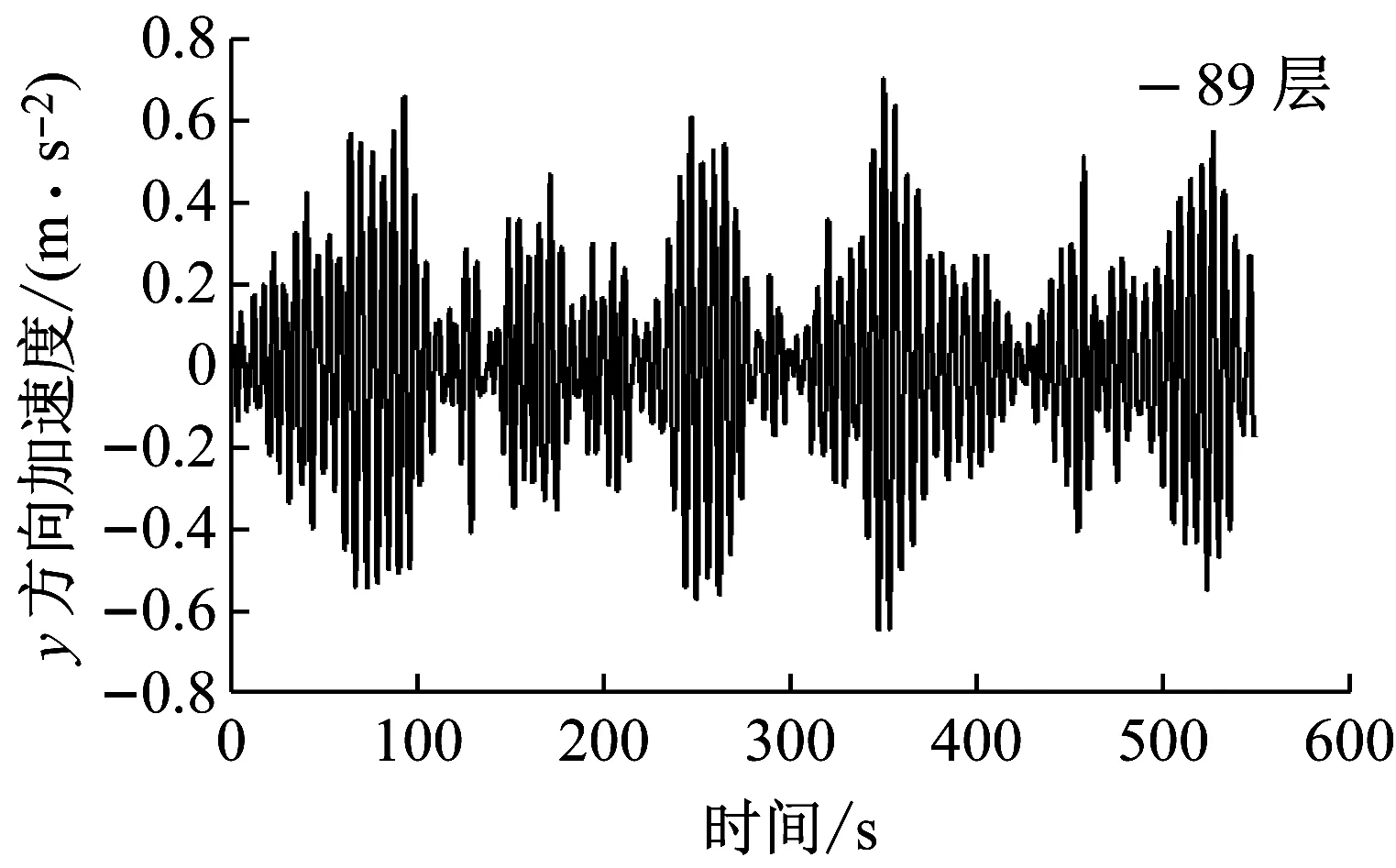
(b)横风向

表2给出了风荷载作用下，计算得到的台北101大楼最高居住楼层(第89层，离地面高度382.2 m)中心处最大加速度响应的结果，同时，风洞试验的结果也列于表2。从表2可以看出：数值计算的结果与风洞试验的结果比较一致，计算结果稍大于试验结果。两者之间的相对误差相差小于13%。

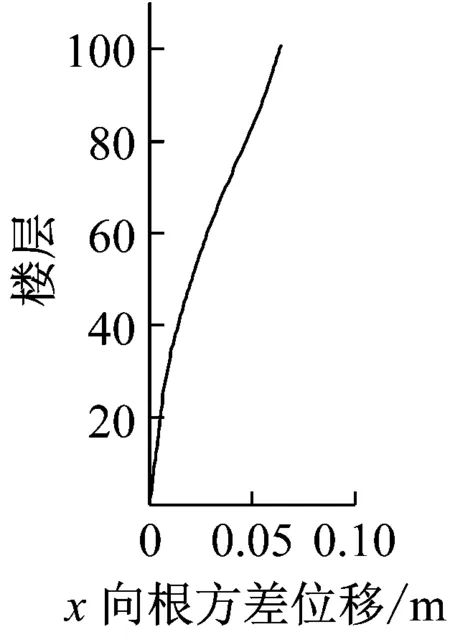
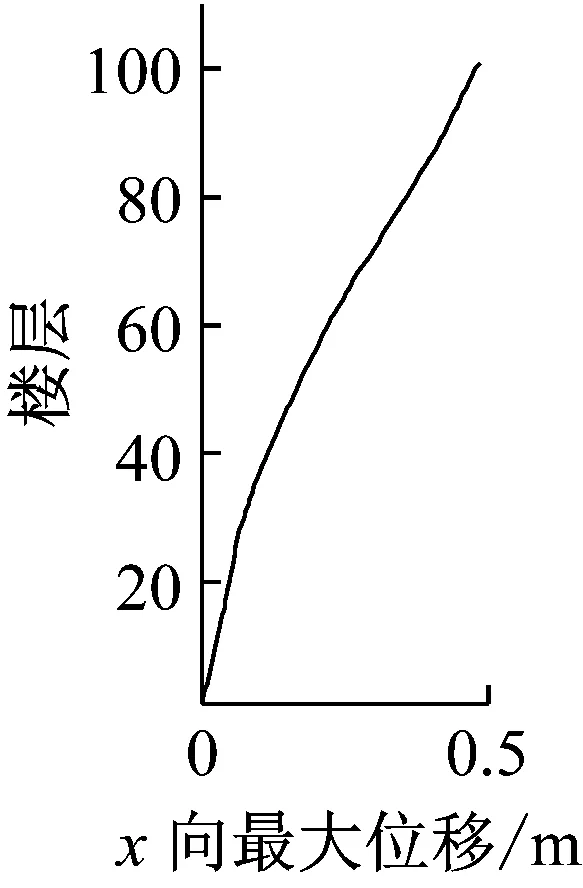
(a)顺风向

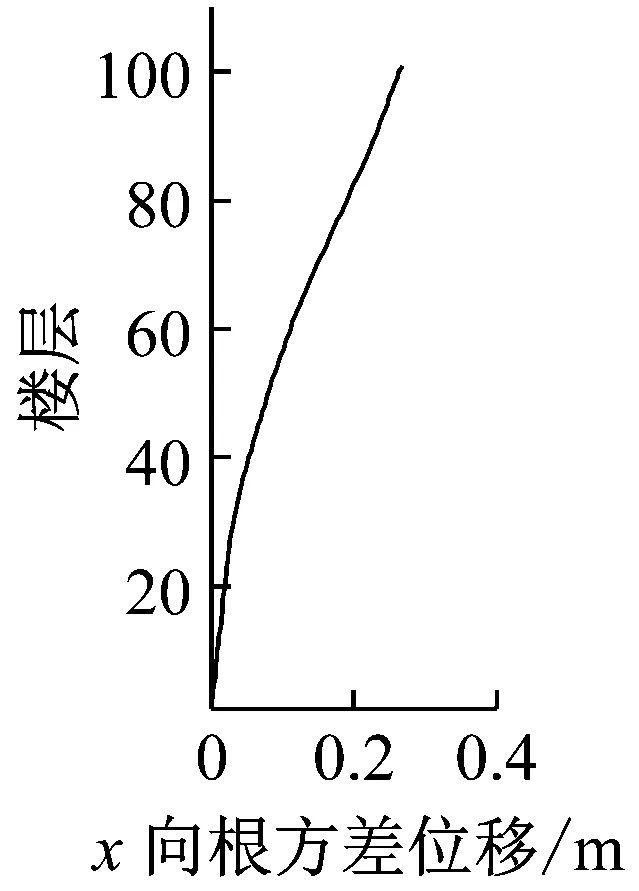
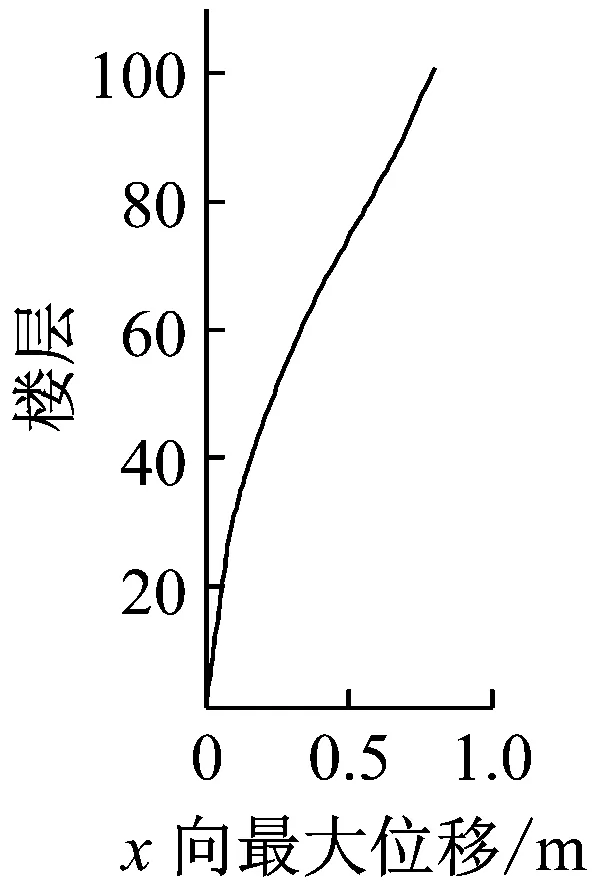
(b)横风向

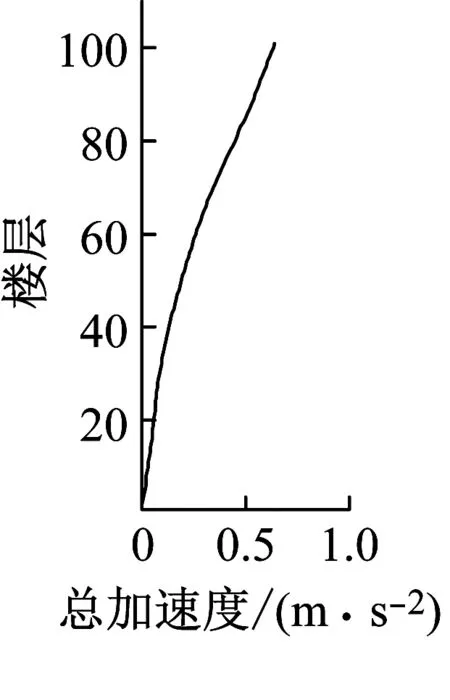
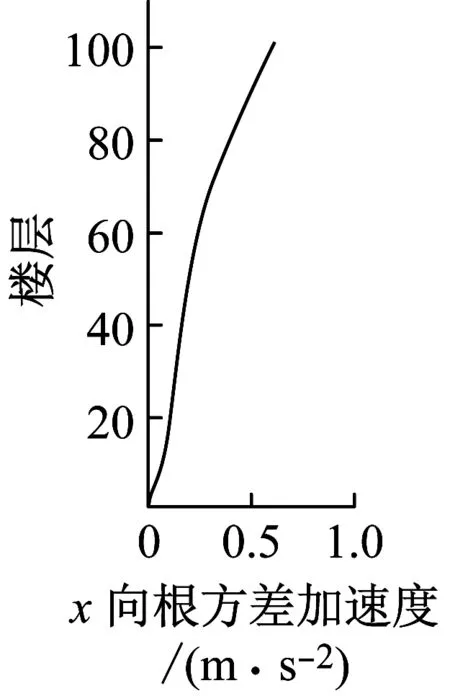
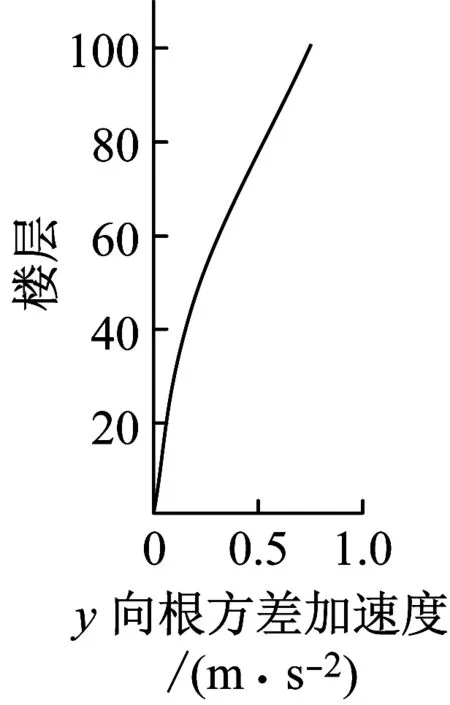
图25 大楼立面上加速度曲线

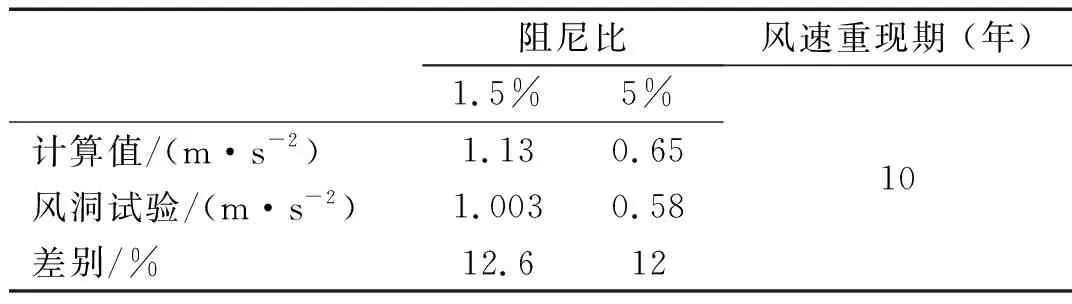
计算值/(m·s-2)风洞试验/(m·s-2)差别/%阻尼比风速重现期 (年)1.5%5%1.130.651.0030.5812.61210

为了研究超高层建筑的风致响应的特性，对大楼不同楼层的位移以及加速度响应进行了功率谱分析。不同楼层处X及Y轴方向上的位移以及加速度响应功率谱如图26～27所示。从图中可看出在0.17 Hz处，各层楼上的位移以及加速度功率谱出现一明显的峰值，这一频率恰好对应大楼的X及Y轴方向上的一阶自振频率。不同层上的位移及加速度功率谱的峰值随着楼层的增高而增加。除了0.17 Hz出现峰值，在0.39 Hz以及0.41 Hz处，顺风向及横风向加速度功率谱还出现了第二个较小的峰值，这两频率也与大楼在这两个方向上的二阶自振频率一致。由此可见：大楼的X及Y轴方向上的位移、加速度响应以一阶频率为主，而二阶频率对大楼加速度响应也有一定影响。

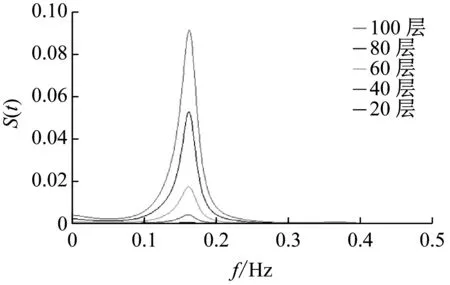
(a)X方向

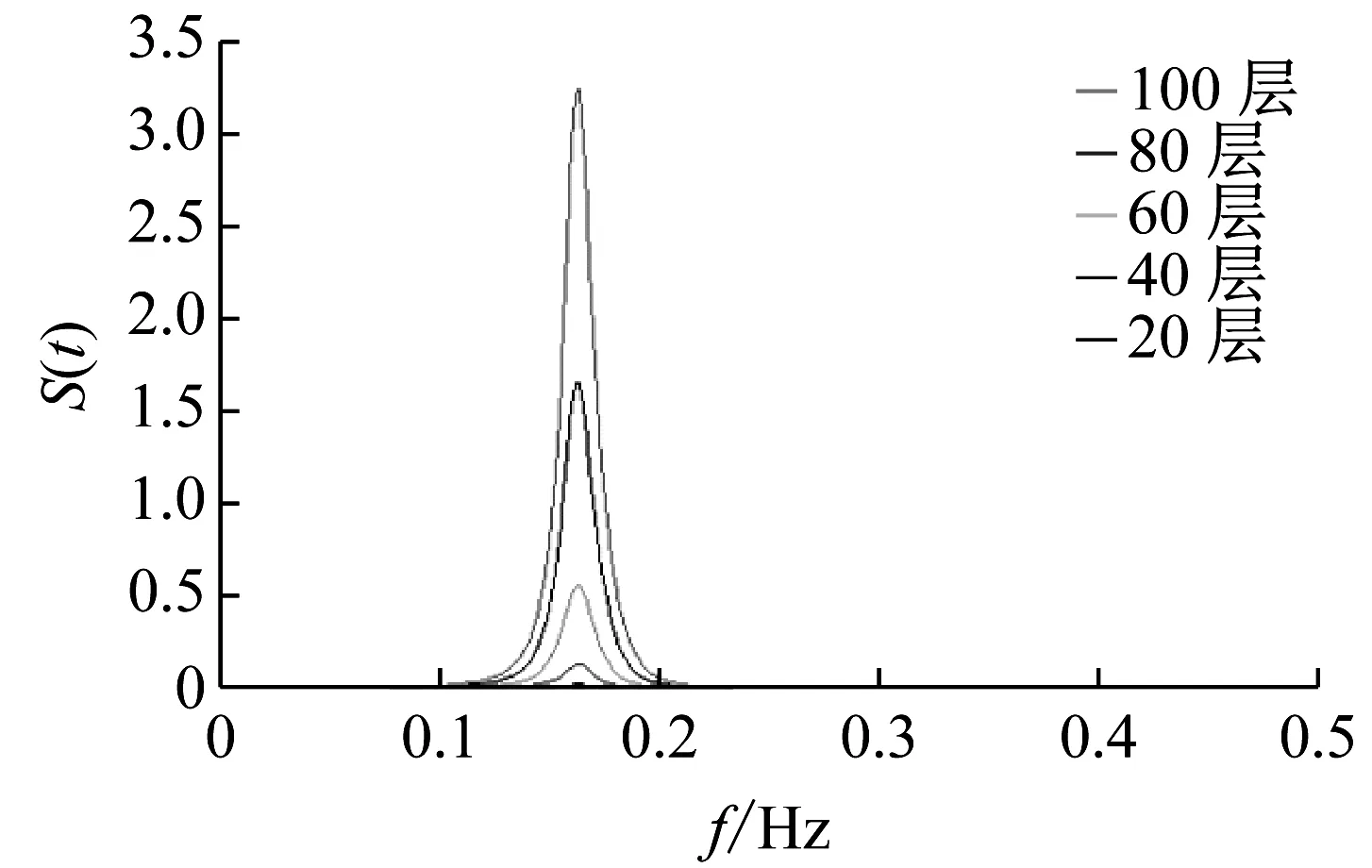
(b)Y方向

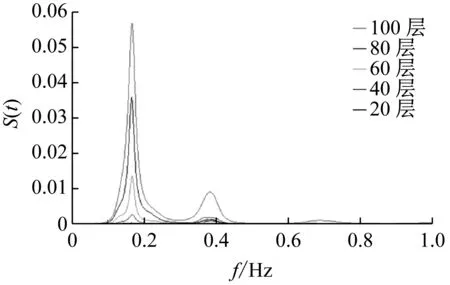
(a)X方向

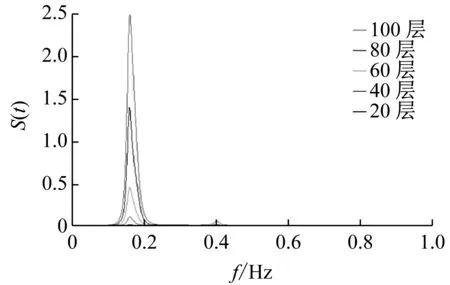
(b)Y方向

计算与现场实测得到的大楼最高居住层第89层处，X及Y轴方向上的加速度功率谱对比如图28所示。从图28中可看出，计算的加速度功率谱与实测谱吻合较好。但在高频部分，计算的加速度功率谱小于实测谱，造成这一差别的原因可能是数值模拟中没有考虑周边建筑，实际风场的湍流强度与数值模拟存在一定差别。

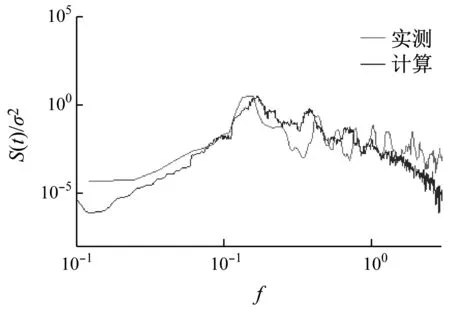
(a)X方向

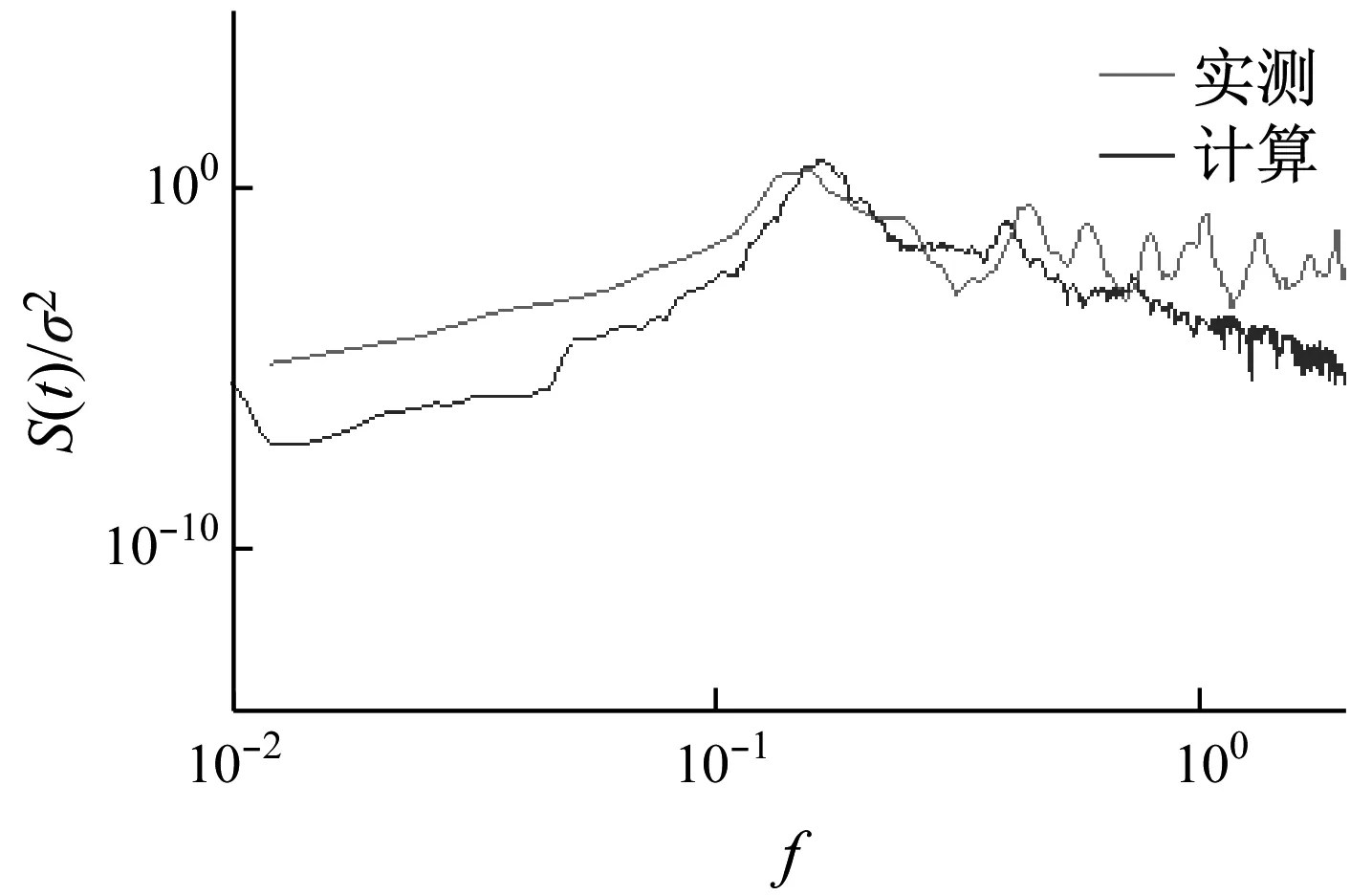
(b)Y方向

Fig.28 Power spectra of the measured and calculated accelerations at the top occupied floor

6 结 论

(1)入口湍流产生的DSRFG方法可以产生满足大气边界层风场特性的卡曼功率谱、LES入口的顺风向湍流强度剖面以及顺风向湍流积分尺度竖向分布的湍流风场。

(2)基于大涡模拟得到的风荷载时程数据作用于台北101大楼的3维有限元模型经过瞬态动力计算得到的大楼风致响应结果与现场实测以及风洞试验结果吻合较好。说明本文的数值模拟方法可以较为准确地模拟高雷诺数流场。

(3)总的来说，运用新的大涡模拟亚格子模型结合合适的湍流入口生成方法能够对高层建筑的风荷载及风致响应进行有效的预测。数值模拟计算结果通过与现场实测与风洞试验结果的对比证明其有较好准确性。数值模拟可为高层建筑结构抗风设计提供有效参考。