线载荷作用下面内运动正交各向异性板的亚谐波共振
胡宇达, 张晓宇, 郝 颖
(1. 燕山大学 建筑工程与力学学院,河北 秦皇岛 066004; 2. 燕山大学 河北省重型装备与大型结构力学可靠性重点实验室,河北 秦皇岛 066004)
复合材料是由有机高分子、无机非金属等几类不同材料通过复合工艺得到的新型材料。实际应用中,层合材料常被做成薄壁结构,在外激励的作用下容易产生大变形,呈现几何非线性。当复合材料结构处于轴向运动等复杂运动条件下时,将会发生由振动引起的共振、混沌等现象,从而存在很多复杂的非线性动力学特性。同时轴向运动结构广泛存在于航空航天、机械、土木工程等工程领域中。所以对轴向运动复合材料板振动问题的研究具有理论和实际意义。对于复合材料层合板的动力学问题,Crabtree等[1]应用有限差分法对预应力层合板的非线性振动进行了数值分析。Houmat等[2]对偏斜层合板的非线性自由振动进行了分析。Udar等[3]研究了非均匀边缘荷载作用下复合材料层合板的组合共振特性。Mergen等[4-5]研究了基于随机系统特性地基上的层合复合材料板的自由振动。胡宇达等[6-7]对于复合材料叠层板的组合共振和非线性组合共振及其分岔进行了分析。周承倜等[8-9]基于复合材料叠层板的非线性动力稳定性理论,对初始缺陷和拉伸-弯曲耦合对于叠层板的振动、屈曲和非线性动力稳定性的影响进行了分析。魏德敏等[10]考虑大挠度和初始几何缺陷的存在,得到了不同边界条件和不同铺设方法叠层板在荷载作用下的突变失稳模型。在轴向运动结构振动问题的研究方面,Banichuk等[11]对轴向运动弹性板的动力稳定性进行了分析。胡宇达等[12-13]研究了磁场环境中轴向运动导电薄板的动力学理论建模问题,并对外磁场作用下轴向运动导流薄板的非线性振动和混沌运动进行了分析。Ghayesh等[14]对轴向运动板受迫运动的非线性动力学进行了数值研究。Zhang等[15]采用复模态分析方法分析了黏弹性地基支承轴向运动梁的横向振动。本文着力于研究面内运动正交各向异性板在线载荷作用下的谐波共振分析,得到稳态运动下关于不同阶模态的共振幅值响应方程,通过数值算例,分析速度、线载荷、材料属性等参量对系统共振特性的影响。
1 正交各向异性板振动方程
正交各向异性板以速度V相对地面水平向右运动,如图1所示,建立空间直角坐标系,Oxy为板的中面,z轴为法向。板在表面x0处受到横向线载荷Fz=f(x-x0)Fsinωt作用,其中,F为外加线载荷幅值,ω为外加载荷频率,f(x-x0)为狄拉克函数,板长度为a,宽度为b,板厚为h,F0x为轴向拉力。
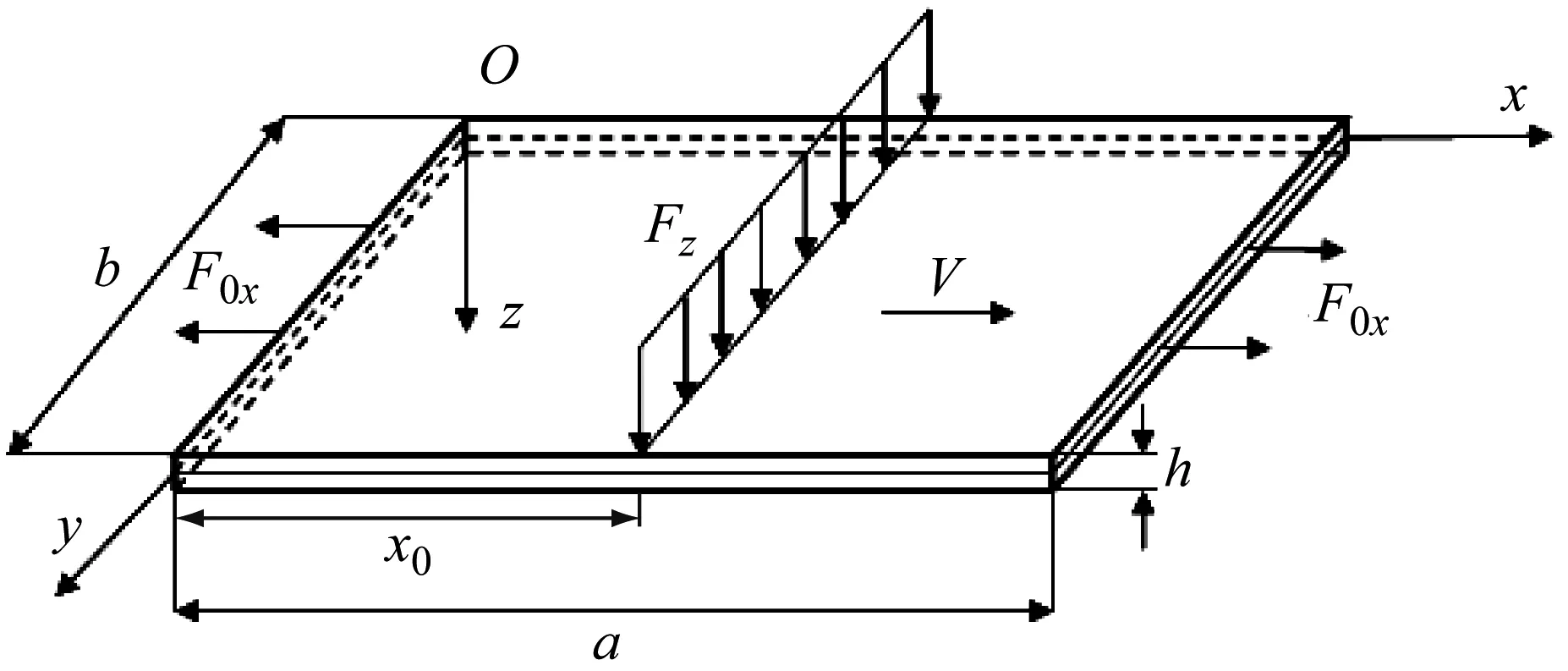
图1 线载荷作用下面内运动板
对于正交各向异性板,非线性几何方程为:

(1)
物理方程:

(2)
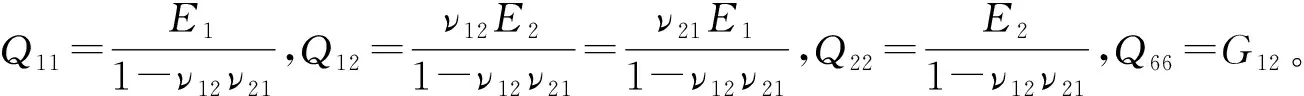
式中:w为板的横向位移;E1为纵向弹性模量(GPa);E2为横向弹性模量(GPa);ν12为纵向泊松比;ν21为横向泊松比;G12为面内剪切弹性模量(GPa)。
考虑几何非线性情况下,横向运动板的动能T、弯曲应变势能U1、中面内力引起的中面应变势能U2、轴向拉力引起的应变势能U3和外力虚功δW有如下表达形式:
(3)
(4)
(5)
(6)
(7)
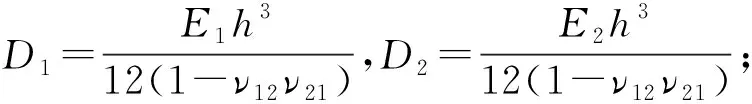
应用哈密顿变分原理,可得如下线载荷作用下面内运动正交各向异性板的横向非线性振动微分方程:
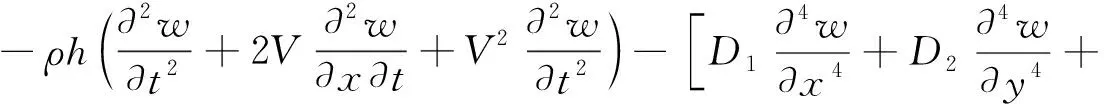
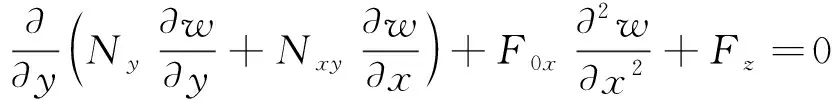
(8)
式中,V为板相对地面在Oxy平面内沿x轴方向的面内运动速度。Nx、Ny、Nxy为正交各向异性板的内力且:

(9)
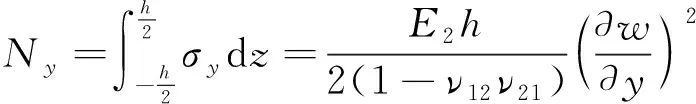
(10)
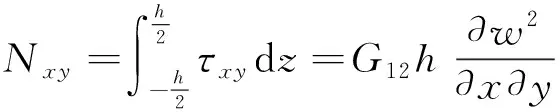
(11)
对于条形薄板的结构特点,由式(8)可以进一步简化得到正交各向异性条形板的横向振动方程:
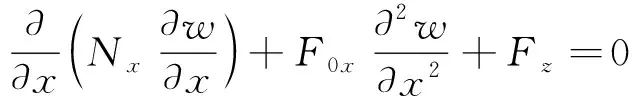
(12)
2 面内运动条形板的亚谐波共振及稳定性分析
2.1 振动微分方程
研究对边(x=0,a)简支面内运动条形板,考虑三阶模态,则位移函数取为

(13)
式中:p1(t)、p2(t)和p3(t)分别为对应阶模态的时间响应函数。
将式(13)代入式(12)中,考虑弱非线性时引入小参数ε,并应用伽辽金法进行积分,设结构阻尼η3,可推得如下仅关于时间变量的无量纲化达芬型非线性振动微分方程:
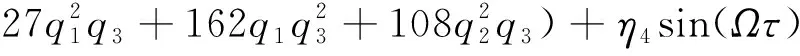
(14a)
η5sin(Ωτ)
(14b)
(14c)

2.2 多尺度法求解1/3亚谐波共振问题
下面运用多尺度法求解系统的1/3亚谐波共振问题。将式(14)的近似解表示为
q1(τ;ε)=q11(T0,T1)+εq12(T0,T1)
(15a)
q2(τ;ε)=q21(T0,T1)+εq22(T0,T1)
(15b)
q3(τ;ε)=q31(T0,T1)+εq32(T0,T1)
(15c)
其中新时间尺度自变量T0=τ,T1=ετ。
将式(15)代入到式(14)中,展开后令两边ε的同次幂相等,得到各阶近似方程:
关于ε0的近似方程:
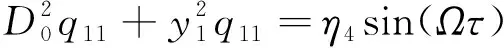
(16a)

(16b)

(16c)
关于ε1的近似方程:
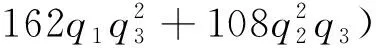
(17a)
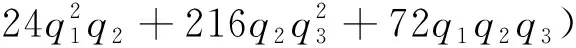
(17b)
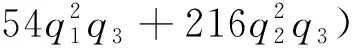
(17c)

设方程(16)的通解形式为

(18a)

(18b)
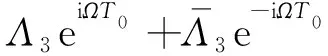
(18c)
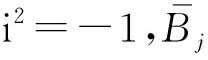
引入调谐参数σ,先求解频率关系Ω=3y1+εσ下的一阶亚谐共振问题。将式(18)代入到式(17)中,为避免久期项,B1、B2、B3需满足:
(19)
式中,B1、B2、B3可以表示为指数形式:

(20)
再将式(20)代入式(19)中,得到:

(21a)
(21b)
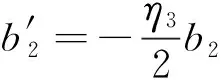
(21c)

(21d)
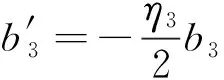
(21e)
(21f)
式中:γ1=σT1-3β1。


(22)
同理可以得到二阶谐波共振(Ω=3y2+εσ)和三阶谐波共振(Ω=3y3+εσ)下稳态解幅值b2、b3的共振响应方程分别为
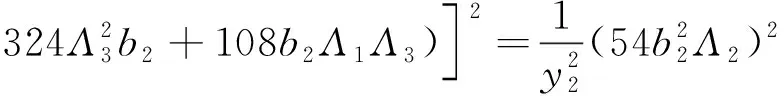
(23)
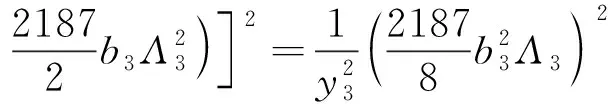
(24)
2.3 稳定性分析
下面对共振系统在稳态运动下定常解的稳定性进行分析,设,
b1=b0+bn,γ1=γ0+γn
(25)
式中:b0、γ0为稳态运动下的定常解,bn、γn为小的摄动量。
将式(25)代入到式(21a)、(21b)中,对bn、γn进行泰勒展开,利用李雅普诺夫第一近似理论,得到一阶共振下判定稳定性的特征方程:
λ2+c1λ+c2=0
(26)
式中:
c1=-η3
同理,可以得到二阶共振和三阶共振下与式(26)相同的特征方程,但系数分别为:
二阶共振:
c1=-η3

三阶共振:
c1=-η3
再根据Routh-Hurwitz判据,可得到三种共振情形下定常稳定解满足的条件为
c2>0
(27)
3 算例分析
下面针对面内运动条形板的亚谐共振问题给出数值算例。参数取为:板长a=0.3 m,轴向拉力F0x=300 kN;材料属性见表1,其中[B(4)/5505]表示硼/环氧复合材料,[T300/5280]和[A5/3501]分别表示不同的石墨/环氧材料。以下算例中除讨论材料参数影响外,其他算例都是硼/环氧复合材料。
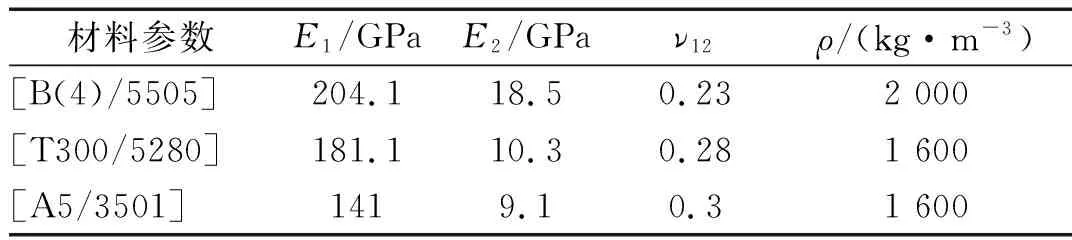
表1 几种复合材料参数
图2~图4分别给出满足Ω=3y1+εσ、Ω=3y2+εσ、Ω=3y3+εσ频率关系下的一阶、二阶和三阶亚谐波共振振幅与频率调谐参数εσ特性曲线图(V=35 m/s,x0=0.075 m,h=2 mm),并分析不同激励力幅值对共振影响。由图可见,图形均为半封闭的双值解曲线,且分为上支和下支,只有当频率调谐参数取一定值时才会激发共振,且随着调谐参数的增大,共振振幅增大。为分析稳定性,在图2~图4中的εσ=0.3处引一条辅助线与曲线分别交于A、B、C、D、E、F六点,以这六点为例,由式(27)对其进行稳定性判定,其值列于表2~表4中。可以判定,图2上支中的A、B、C三点为稳定解,下支中D、E、F为不稳定解;图3上支和下支既有稳定解又有不稳定解,其中A、B点为稳定解,C、D、E、F为不稳定解;图4中A、B、C、D、E、F则都为不稳定解。可见系统上支和下支曲线所对应解的稳定性具有复杂的变化规律。
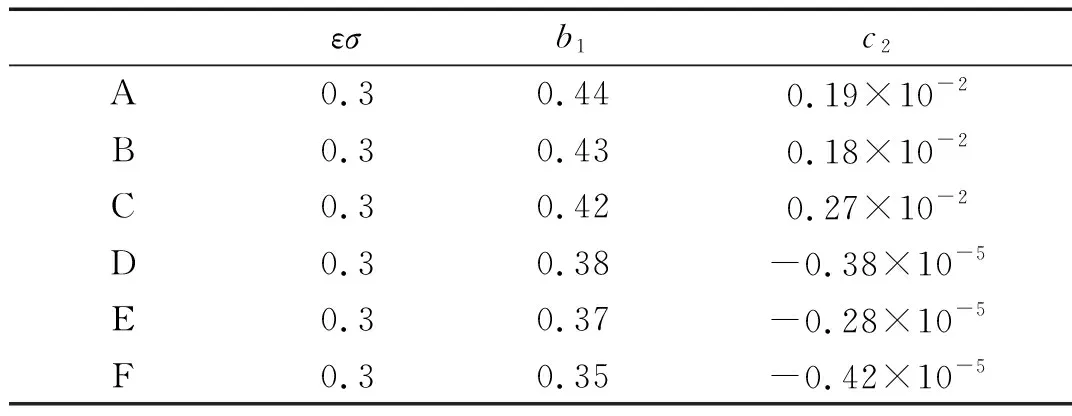
表2 一阶振幅-调谐参数稳定性判定值

表3 二阶振幅-调谐参数稳定性判定值

表4 三阶振幅-调谐参数稳定性判定值
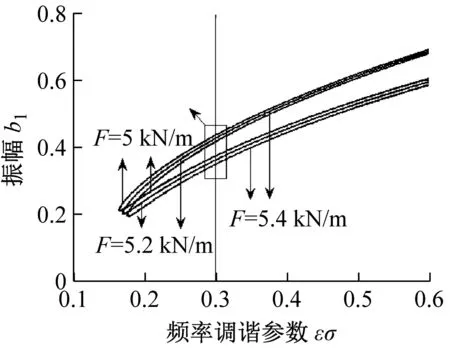
图2 一阶振幅-调谐参数曲线图
图5给出了比较不同模态所对应前三阶振幅的幅频响应曲线图,其中1、2、3分别表示一阶、二阶和三阶振幅-调谐参数曲线。由图可以看出,一阶模态对应的振幅较大,对系统振动影响明显,而二阶、三阶模态对应的幅值逐渐减小,对系统振动影响逐渐减弱。

图3 二阶振幅-调谐参数曲线图

图4 三阶振幅-调谐参数曲线图
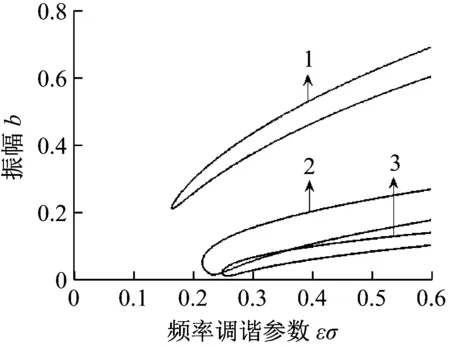
图5 振幅-调谐参数曲线比较图
图6~图8分别给出了开始激发一阶、二阶和三阶共振时的参数临界点变化曲线图。如图6所示,对一阶系统,当激励力幅值F<4 000 N/m时,随着频率调谐参数的减小,激发共振所需的激励力的幅值在增大,而当激励力幅值F>4 000 N/m时,则随着频率调谐参数的增大,激发共振所需的激励力的幅值在增大。如图7和图8,二阶和三阶系统激发共振临界点都随着频率调谐参数的增大呈现递增的趋势。

图6 一阶激发共振临界点变化曲线
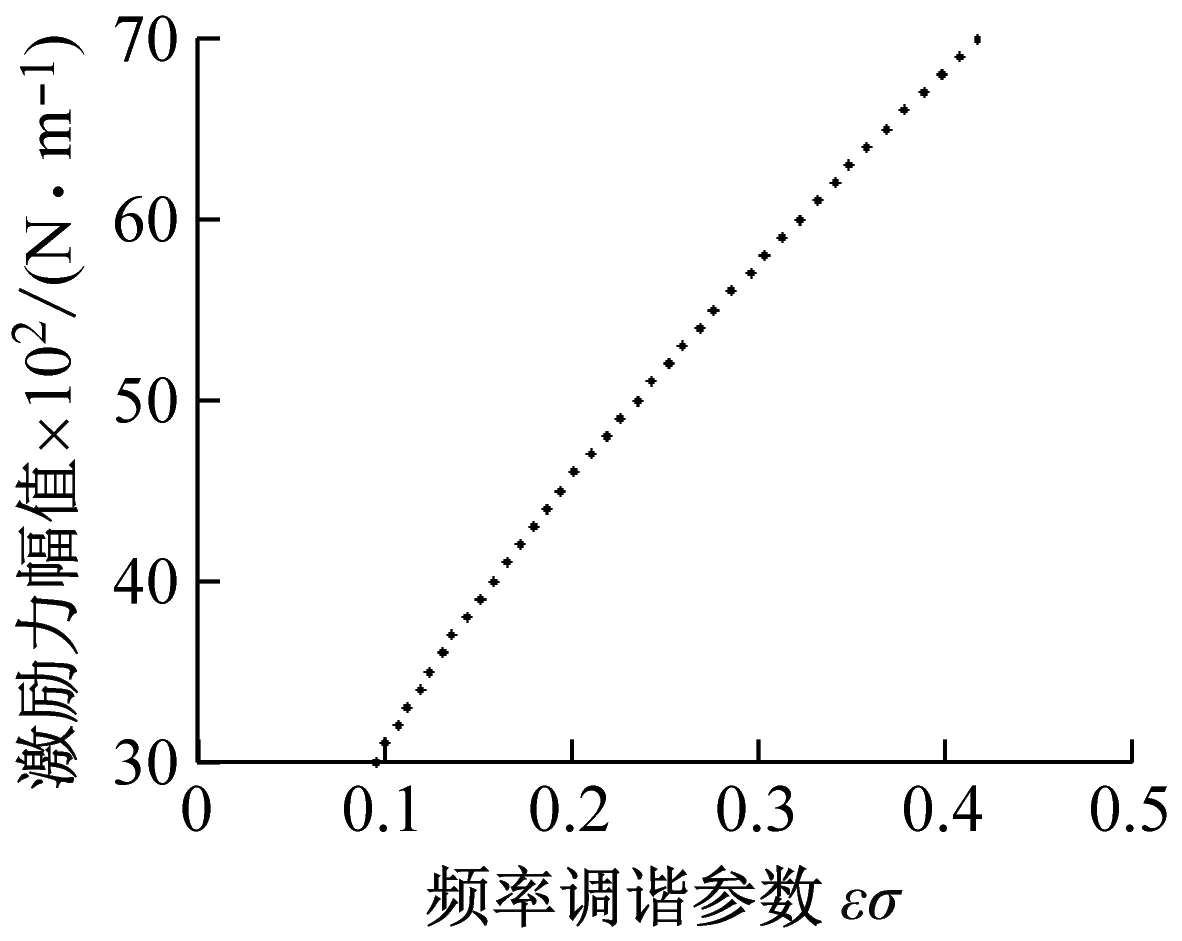
图7 二阶激发共振临界点变化曲线
图9~图11同样给出一阶、二阶、三阶亚谐波共振振幅与频率调谐参数εσ特性曲线图。其中(a)、(b)、(c)、分别表示速度、材料与激励力位置对于亚谐波共振的影响。由图可见,随着频率调谐参数的增加,共振激发后振幅均呈现整体递增的趋势;不同速度和材料参数值的改变对共振解的多值性及其初始共振激发点均有显著影响;激励力位置的改变对振幅的影响也很明显,且当x0=0.15 m时的二阶共振现象不会被激发。

图8 三阶激发共振临界点变化曲线

(a) 不同速度(F=5 kN/m,x0= 0.075 m,h=2 mm)
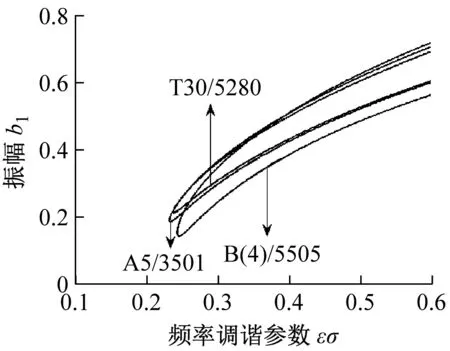
(b) 不同材料(V=35 m/s,h=2 mm,x0= 0.075 m,F=5 kN/m)

(c) 不同激励力位置(V=35 m/s,h= 2 mm,F=5 kN/m)
图9 不同参量下一阶振幅-调谐参数特性曲线
Fig.9 First-order amplitude-detuning parameter curves of different parameters

(a) 不同速度(F=5 kN/m,x0= 0.075 m,h=2 mm)

(b) 不同材料(V=35 m/s,h=2 mm,x0= 0.075 m,F=5 kN/m)
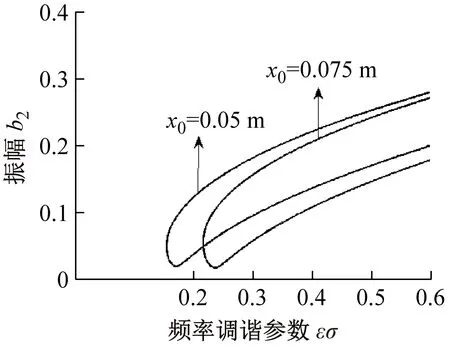
(c) 不同激励力位置(V=35 m/s,h= 2 mm,F=5 kN/m)
图10 不同参量下二阶振幅-调谐参数特性曲线
Fig.10 Second-order amplitude-detuning parameter curves of different parameters
图12~图14分别给出一阶、二阶、三阶亚谐波共振振幅与激励力幅值特性曲线图,虚线区域之间表示系统激发共振区域。由图可见,曲线为月牙形的光滑封闭曲线,随着激励力的幅值F的增加,亚谐波共振的振幅呈现递减的趋势;随着调谐参数εσ的增大,共振幅值的取值范围也变大变宽,其共振波的振幅也随之增大。为分析解的稳定性,在图12中的F=4 500 N/m处引一条辅助线与曲线交于A、B、C、D、E、F六点,以这六点为例由式(27)对其进行稳定性判定,由列于表5的值可知,上支点A、C、E的解是稳定的,下支点B、D、F的解是不稳定的。同样,在图13和图14中的F=3 000 N/m处分别引辅助线与曲线交于A、B、C、D、E、F六点进行稳定性判别,由表6和表7的数值可知,二阶共振下A、B、C、D、E、F解都是稳定的,三阶共振下A、B、C三点为稳定解,D、E、F三点为不稳定解。
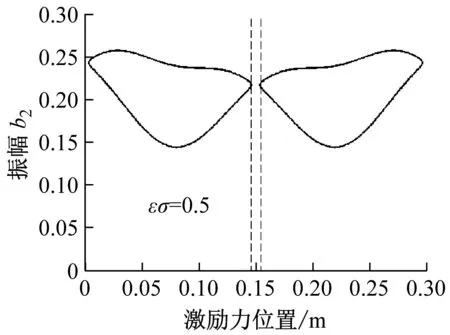
图15~图17分别给出了不同频率调谐参数下一阶、二阶、三阶振幅随激励力作用位置变化曲线图(取V=35 m/s,h=2 mm,F=5 kN/m)。由图可以看出,在板的边缘附近振动不会被激发,所有曲线关于载荷位置x0=0.15 m对称;图像由多个封闭的双值曲线组成,图中虚线之间表示共振区域窗口,在虚线间的空白区域系统的亚谐波共振不会被激发,随着激励力位置的变化,共振区域与非共振区域交替变化,并且呈现不同的共振区域窗口。同时可见,频率调谐参数对曲线形状有显著影响,一阶和二阶下的图15(a)和图16(a)中曲线呈月牙形,存在6个和4个共振区域;图15(b),(c)和图16(b),(c)中图形呈凹形,分为3个和2个共振区域,且都是随着激励力位置的变化,振幅先减小后增大;图17(a)中图形由两个月牙形和一个卵形组成,而图17(b),(c)中曲线呈波浪形,表明载荷位置对共振幅值解的影响较大。

(a) 不同速度(F=5 kN/m,x0= 0.075 m,h=2 mm)

(b) 不同材料(V=35 m/s,h=2 mm,x0= 0.075 m,F=5 kN/m)
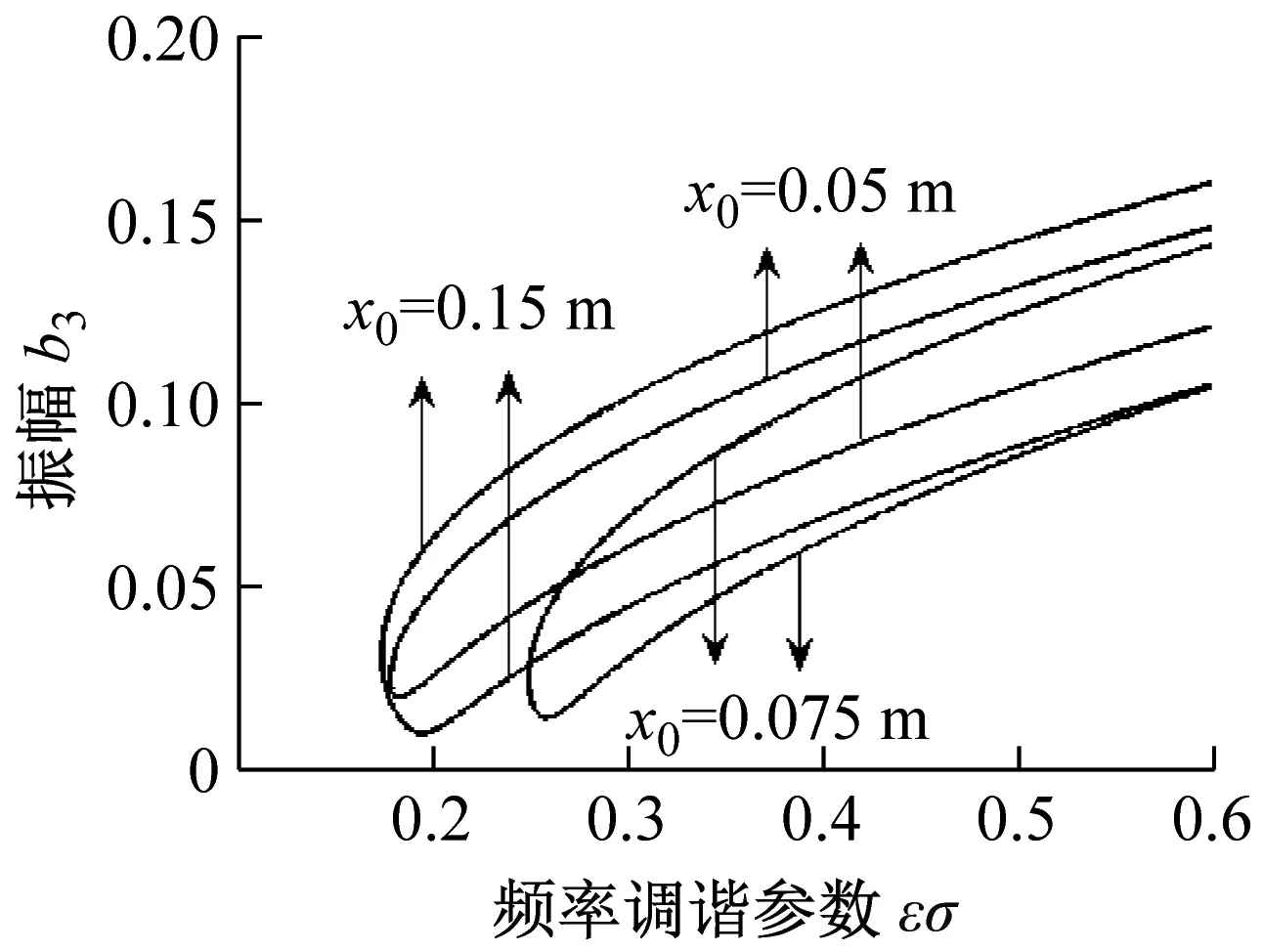
(c) 不同激励力位置(V=35 m/s,h= 2 mm,F=5 kN/m)
图11 不同参量下三阶振幅-调谐参数特性曲线
Fig.11 Third-order amplitude-detuning parameter curves of different parameters

图12 一阶振幅-激励力幅值曲线图
Fig.12 First-order amplitude-excitation force amplitude parameter curves

图13 二阶振幅-激励力幅值曲线图
Fig.13 Second-order amplitude-excitation force amplitude parameter curves

图14 三阶振幅-激励力幅值曲线图
Fig.14 Third-order amplitude-excitation force amplitude parameter curves

表5 一阶振幅-激励力幅值稳定性判定值

表6 二阶振幅-激励力幅值稳定性判定值

表7 三阶振幅-激励力幅值稳定性判定值

(a) εσ=0.2

(b) εσ=0.3

(c) εσ=0.5
图15 一阶振幅-激励力位置特性曲线
Fig.15 First-order amplitude-excitation force position curves

(a) εσ=0.2
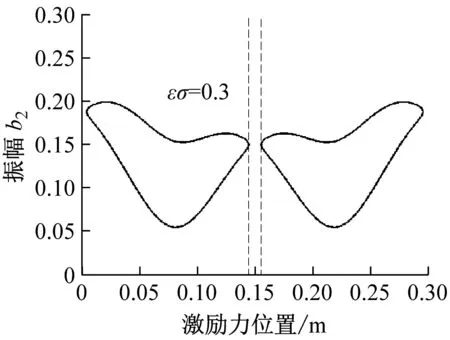
(b) εσ=0.3
(c) εσ=0.5
图16 二阶振幅-激励力位置特性曲线
Fig.16 Second-order amplitude-excitation force position curves

(a) εσ=0.2

(b) εσ=0.3
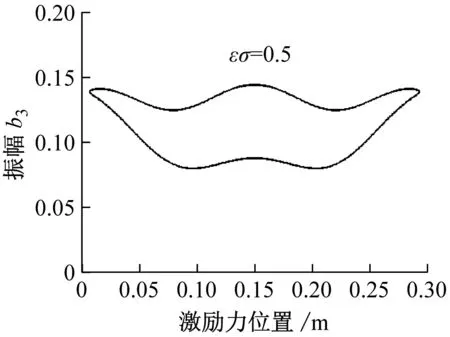
(c) εσ=0.5
图17 三阶振幅-激励力位置特性曲线
Fig.17 Third-order amplitude-excitation force position curves
4 结 论
本文以线载荷作用下面内运动正交各向异性为研究对象,得到非线性亚谐波共振下系统的共振响应解及稳定性判定式。数值算例结果表明:
(1) 当系统发生亚谐波共振时,随着频率调谐参数的增加,共振激发后振幅均呈现整体递增的趋势;不同速度和材料参数值的改变对其初始共振激发点有显著影响。
(2) 随着线载荷的幅值F的增加,亚谐波共振的振幅呈现递减的趋势;线载荷作用位置对共振幅值影响明显,并呈现曲线对称和间隙激发共振现象。

