基于叠加和频谱分析的电子雷管延期时间研究

龚 敏， 石发才， 吴晓东

(北京科技大学 土木与资源工程学院，北京 100083)

在小净距隧道爆破开挖中，爆破振动会对已建隧道衬砌和中夹岩造成很大的影响，甚至会引起一定的安全隐患[1-2]。对此，使用常规的导爆管雷管进行控制时，由于可用段数较少，有时效果不好。这种情况下，延期时间可以灵活设置的电子雷管为有效降低爆破振动提供了可能性[3]。使用电子雷管进行微差爆破时，电子雷管延期时间的合理设置对有效降低爆破振动尤为重要。一般来说，延期时间过大会降低爆破作用的协同性，延期时间过小会使爆破振动大幅提高。如何识别雷管的实际延期时间和获得电子雷管的最佳延期时间，从而有效控制爆破振动仍然是当前的热门课题。学者们对此进行了大量研究，取得了一定的成果。

准确识别雷管的实际延期时间，可以为爆破设计优化提供依据。目前主要采用基于EMD-HHT和小波分析的奇异性检测法识别雷管的实际延期时间。如龚敏等[4]利用基于EMD-HHT的瞬时能量法和EMD法对雷管起爆时刻识别进行了识别，对比了两种方法的识别效果。张胜等[5]采用模式自适应小波时能密度法对微差爆破的实际延期时间进行了确定。对于电子雷管的最佳延期时间，目前主要采用理论计算法、数值模拟法和现场实测法进行确定。理论计算法，即根据各种理论推导出相关理论公式，从而根据炸药参数和现场的围岩参数等进行最佳延期时间的确定。如李清等[6]基于充分形成新自由面的原则，提出了精确控制爆破延期时间的理论计算公式，在工程中得到了很好的应用。李顺波等[7]基于弹性波理论给出了毫秒延期时间计算公式。数值模拟法即采用动力分析软件模拟爆破，对比不同延期时间下监测点处的爆破振动，从而进行最佳延期时间的确定。如楼晓明等[8]利用LS-DYNA建立了0 ms、17 ms、25 ms和42 ms四种不同延期时间下的台阶爆破模型，发现延期时间为25 ms时，降振效果明显。现场实测法即通过现场做单孔试验，再基于线性叠加原理和半周期减振原理确定电子雷管的最佳延期时间。如崔正荣等[9]通过叠加现场实测的单孔波形，得到最佳延期时间为23 ms。田振农等[10]采用电子雷管起爆，认为延期时间设置为1/2倍主周期时，能有效降低爆破振动。由于现场条件多变，理论计算和数值模拟有时难以得到可靠的结果，而现场实测法获得的结果更符合实际情况。利用实测法确定电子雷管的最佳延期时间时，如果能建立线性叠加原理和半周期减振原理间的联系，便可以综合利用两种方法，获得更加可靠的电子雷管延期时间，从而更有效地降低爆破振动。

本文对莲塘超小净距隧道混合起爆网络中的振动波形进行研究，采用EMD-HHT法和小波分析法进行奇异性检测，从而识别出各段雷管起爆时刻，分离出单孔波形。然后对单孔波形进行线性叠加分析和频谱分析，分析合成波形的特点，观察各单孔波形的主频特点。最后探究合成波形振速峰值最小、较小和最大时对应的延期时间和主周期间的联系，从而得到一种更加可靠的电子雷管最佳延期时间确定方法，为有效降低爆破振动提供依据。

1 研究方法

1.1 EMD-HHT方法

EMD-HHT方法是在EMD分解的基础上，利用Hilbert变换得到各分量的瞬时频谱，从而可同时分析信号时频特征的一种方法。具体操作步骤如下[11]：

1.1.1 EMD分解

对原始信号X(t)，首先找出所有极值点。然后用三次样条曲线对所有的极大值点进行插值，从而拟合出原始信号X(t)的上包络线。同理，拟合出X(t)的下包络线。上下包络线包含了所有的原始信号数据。然后，求出上下包络线的均值，并按顺序连接得到一条均值线m1(t)，再用X(t)减去m1(t)，得到h1(t)如下

h1(t)=X(t)-m1(t)

(1)

若果h1(t)同时满足如下条件(1)和(2)，即认为h1(t)是一个IMF分量。

(1) 整个数据序列中，过零点的数量与极值点的数量相等或至多相差1。

(2) 信号上任意一点，由局部极小值点确定的包络线和由局部极大值点确定的包络线的均值均为0，即信号关于时间轴对称。

1.1.2 Hilbert变换

EMD分解完成后，对每个IMF分量c(t)作Hilbert变换，得到H(c(t))

(2)

式中:PV代表柯西主值。然后构造信号z(t)

z(t)=c(t)+jH(c(t))=a(t)ejφ(t)

(3)

式中:a(t)为幅值函数，Φ(t)为相位函数。

定义Hilbert谱的表达式为

(4)

定义Hilbert瞬时能量谱的表达式为

(5)

1.2 小波分析

小波分析方法是一种时间窗和频率窗都可以改变的时频局部化分析方法。

设ψ(t)∈L2(R)，其傅里叶变换为F(w)。当F(w)满足

(6)

时，称ψ(t)为一个母小波。将母小波平移和伸缩后，就可以得到一个小波序列。

连续小波为

(7)

对于任意函数f(t)∈L2(R)的连续小波变换为

(8)

实际中常用的小波为离散2进小波，即a=2j，b=2jk(j，k∈Z)。

1.3 傅里叶变换

傅里叶变换是可以将信号在时域和频域间相互转化的工具。傅里叶变换的实质是将f(t)分解成不同频率正弦波的叠加，这样就把对f(t)的研究转化为对其加权系数F(w)的研究。通过将爆破振动时域信号转换为频域信号，可以很好地分析信号的频域特征。

函数f(t)∈L2(R)的连续傅里叶变换定义为

(9)

实际应用中常用的是离散傅里叶变换(DFT)，离散时间序列{fn}的DFT定义如下

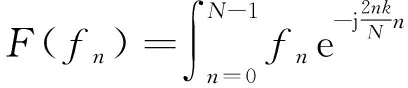
(10)

式中:k=0，1，…，N-1。

1.4 叠加分析

为了进行叠加分析，从原振动波形中截取得到单孔波形。单孔波形的持续时间为T0，采样间隔为dt，每个采样点的振速值为g′(t)。由于采集到的波形为离散数据点，为了程序计算方便，将单孔波形数据点拟合成傅里叶级数形式

(11)

式中:t为时间；n为级数；w0为基频；a0、an，bn为拟合参数。表达式如下

w0=2π/T0

(12)

(13)

将g(t)扩展到整个时间域，得到

(16)

根据Anderson、Hizen和谢烽等[12～14]的研究，可知利用线性叠加原理预测爆破振动是可行的。假设每个孔药量相同，单孔波形为f(t)，微差爆破的延期时间为Ti，则m个炮孔微差爆破后的振动波形可表示为如下形式

(17)

通过上述叠加，可以得到不同延期时间下合成波形f′(t)的振速峰值及其在合成波形中出现的时刻，从而可以研究延期时间和合成波形振速峰值间的关系。当合成波形的振速峰值最小时，对应的延期时间即为最佳延期时间。

2 信号的奇异性检测

2.1 小波基函数的选取

选择合适的小波基函数对于提高信号奇异性检测效率有很大的帮助。一般可根据小波基函数的性质(紧支性、正则性、对称性和消失距)进行小波基函数的选取。根据研究[15-17]，小波基函数衰减越快，局部化特性就越好。正则性表现为小波基函数的可微性，一定的正则性和足够高的消失距对有效检测信号奇异性非常重要。而过高阶的消失距会增加计算量，并使分析结果模糊。对称性可保证信号重构时的精确性，在进行信号奇异性检测时，可放松这方面的要求。

根据上述要求，可选择db3小波基函数进行信号的奇异性检测。相对于其他db系列小波，db3小波基函数紧支集较小，时域紧支性好，近似对称，有3阶消失距，有利于检测信号的奇异性，同时计算量较小。

2.2 奇异性检测实例

某次爆破开挖的实际炮孔布置见图1。为了防止风钻钻孔角度问题带来的欠挖，设置图1中所示的补偿炮孔(未填充的孔)。为了使掌子面底部爆破达到单孔单响的要求，增加一个550 ms的电子雷管。1 050 ms和1 170 ms为设计的单孔试验。为了防止串段和获得足够的单孔波形，设计非电雷管跳段使用。在水平方向距离开挖轮廓线3.5 m处测得的X方向振动波形见图2，从图2可以大概看出各段振动波形有明显的区分，其中振动信号的采样频率为8 000 Hz。为了精确确定各段的起爆时刻，对X方向的振动波形进行EMD-HHT和db3小波分析(分解8层)，得到Hilbert瞬时能量谱图3、主成分分量IMF2的Hilbert包络曲线图4、小波分析时能密度曲线图5和小波变换模值(第3层)图6。各方法的识别结果统计于表1。由于电子雷管的误差为±1.5 ms，所以电子雷管起爆时刻550 ms和1 050 ms可以作为很好的识别性能评价标准。从表1中不难看出，EMD法(主成分包络法)和小波分析模极大值法较为精确地识别出了非电雷管各段的起爆时刻，识别结果符合非电雷管段数及延期时间误差图7，但是四种方法对于延期时间为6 ms的电子雷管(1 250～1 424 ms)的识别均较为粗糙。从图3和图5可以看出，电子雷管(1 250～1 424 ms)爆破的瞬时能量较大，所以有必要充分利用电子雷管的延时精确性，错相减振，降低爆破振动，而合理设置电子雷管延期时间是达到上述要求的关键。结合表1和图2可以看出，第五段和第十一段有100 ms左右的衰减时间，基本衰减为0，而且前一段振动基本衰减为0。因此可以认为第五段、第十一段以及1 050 ms处的波形为完整的单孔波形，且没有叠加其他波形(除噪音)。从而得到第五段、第十一段和1 050 ms处X方向的单孔波形见图8，由于篇幅限制，其他方向的单孔波形不再给出。

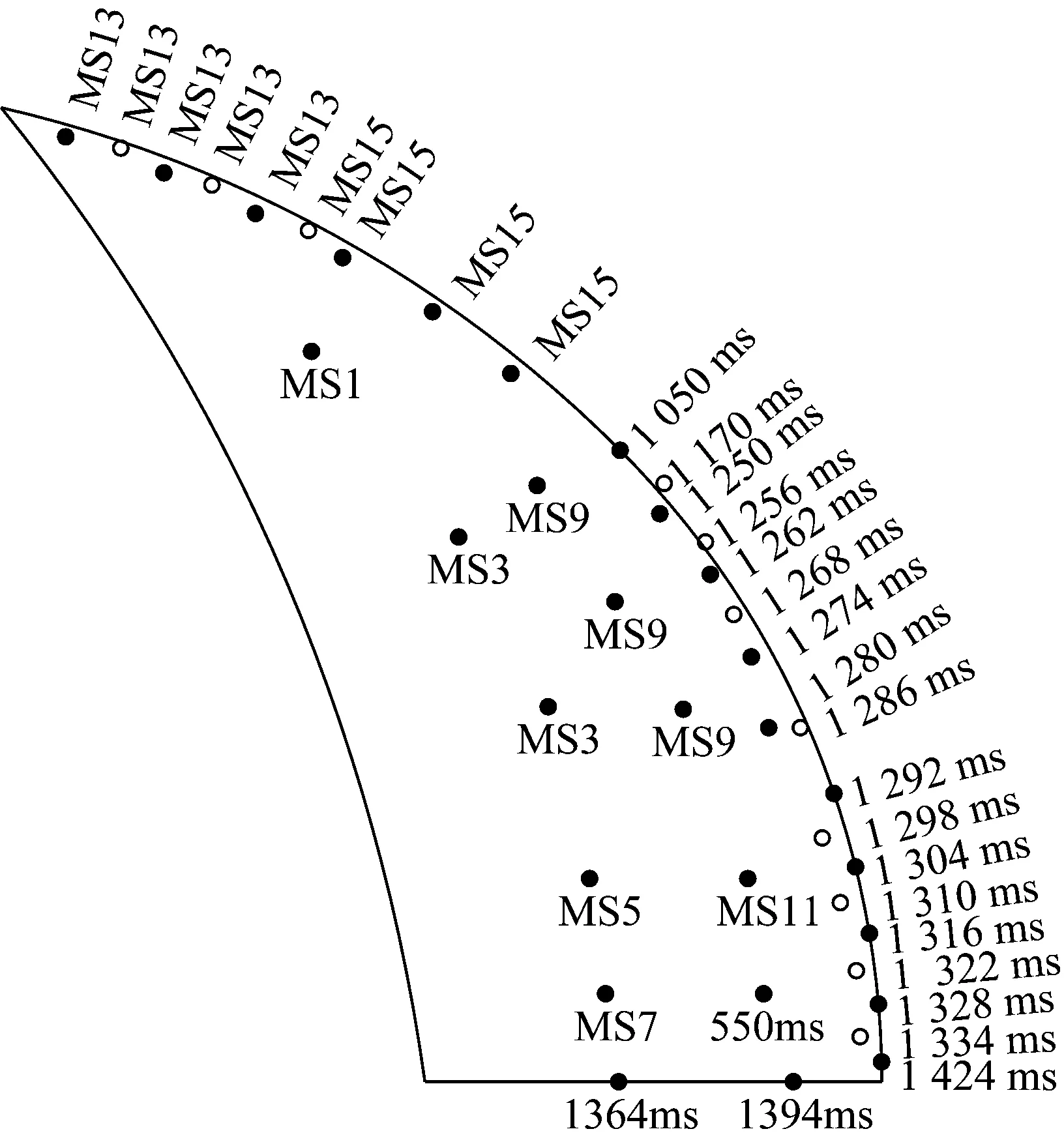
图1 实际炮孔布置图

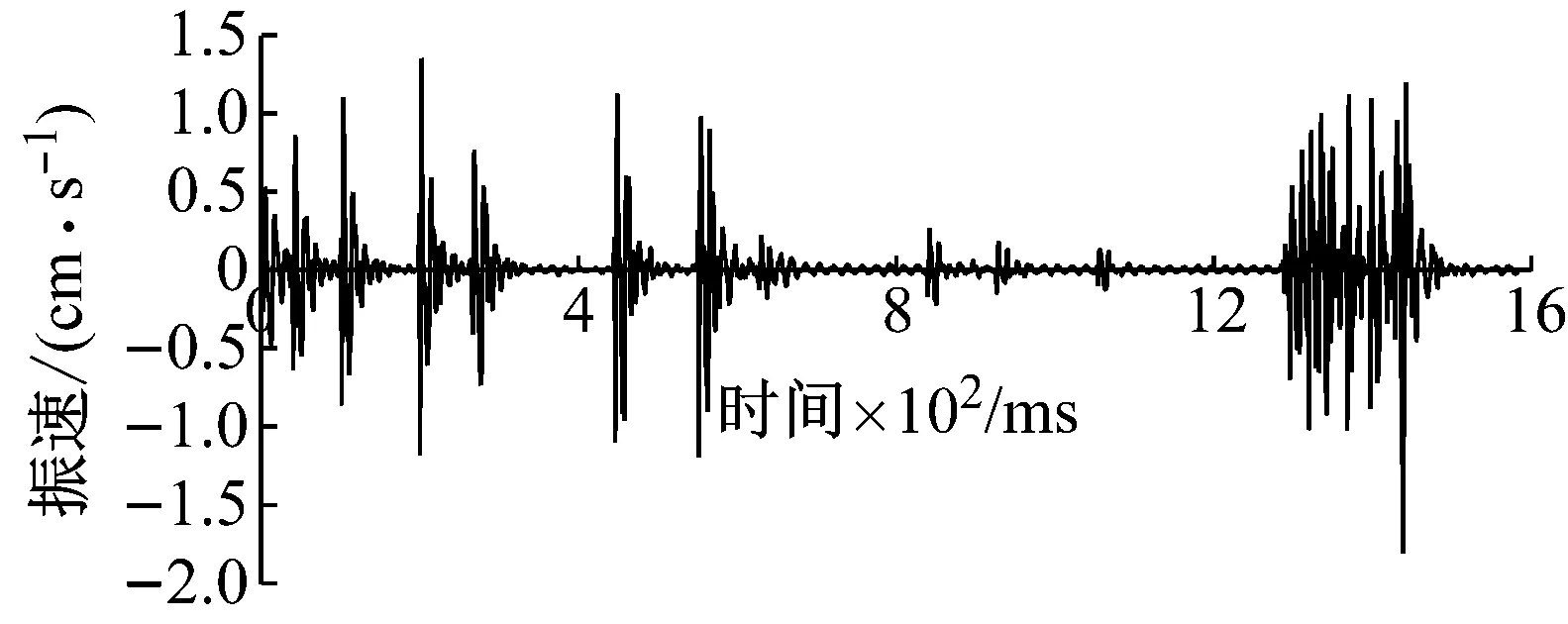
图2 X方向振动波形

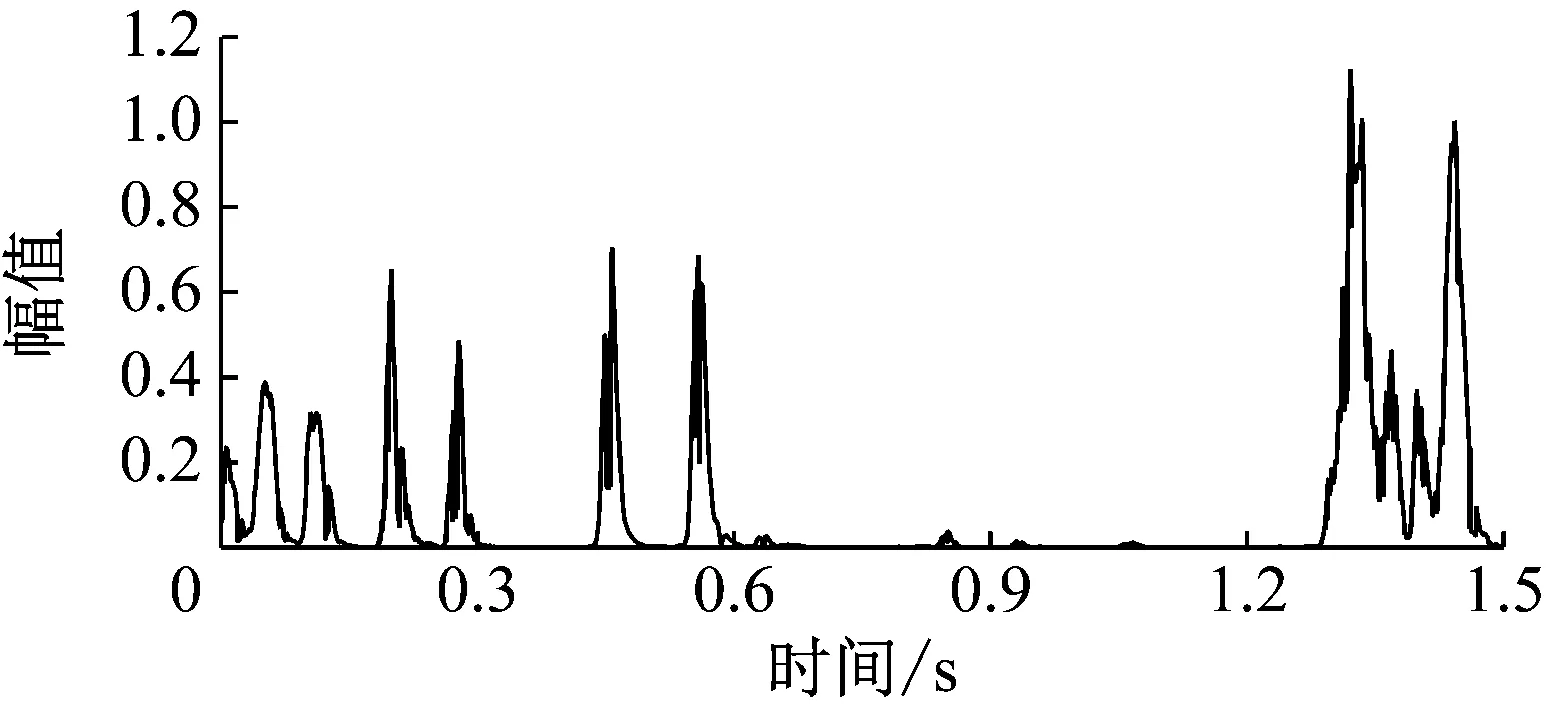
图3 Hilbert瞬时能量谱

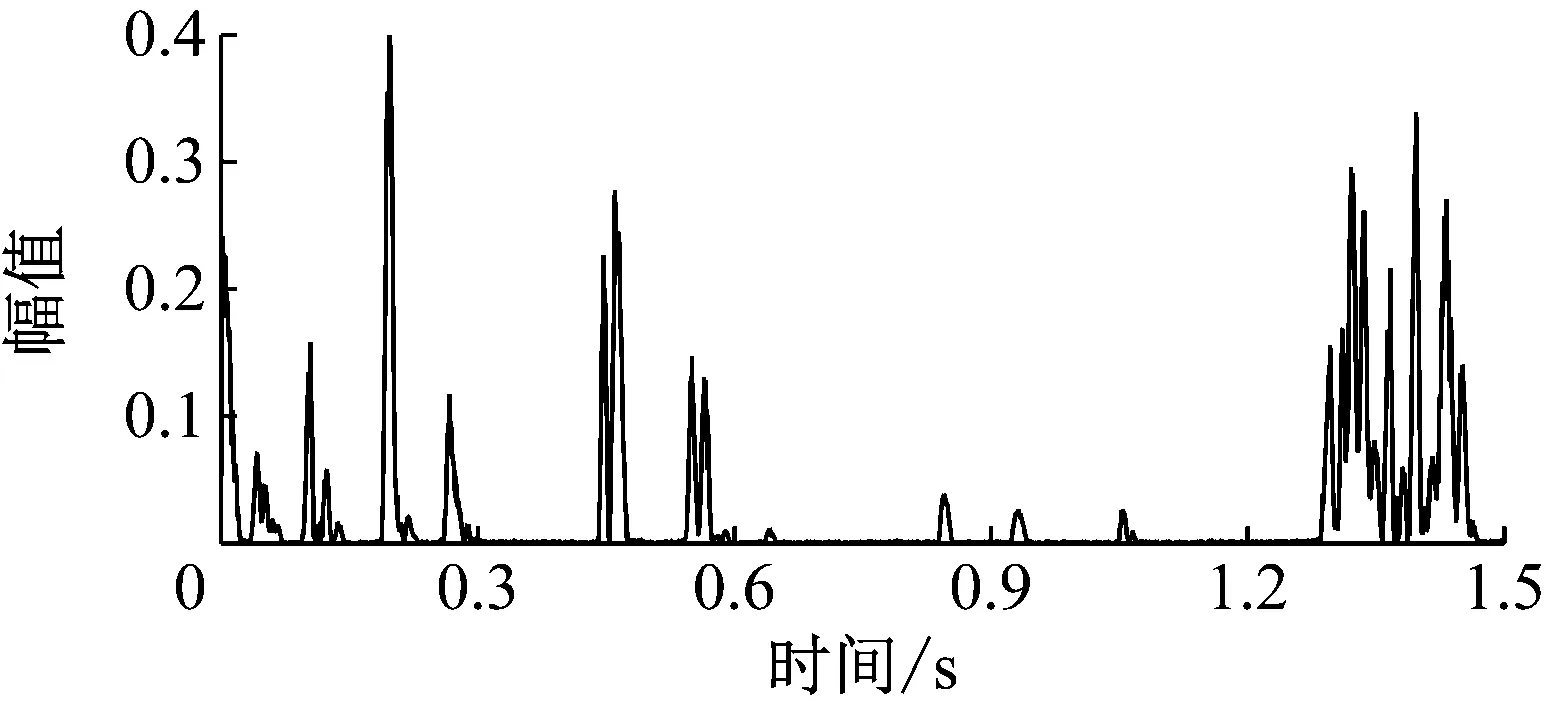
图4 主成分包络曲线(IMF2)

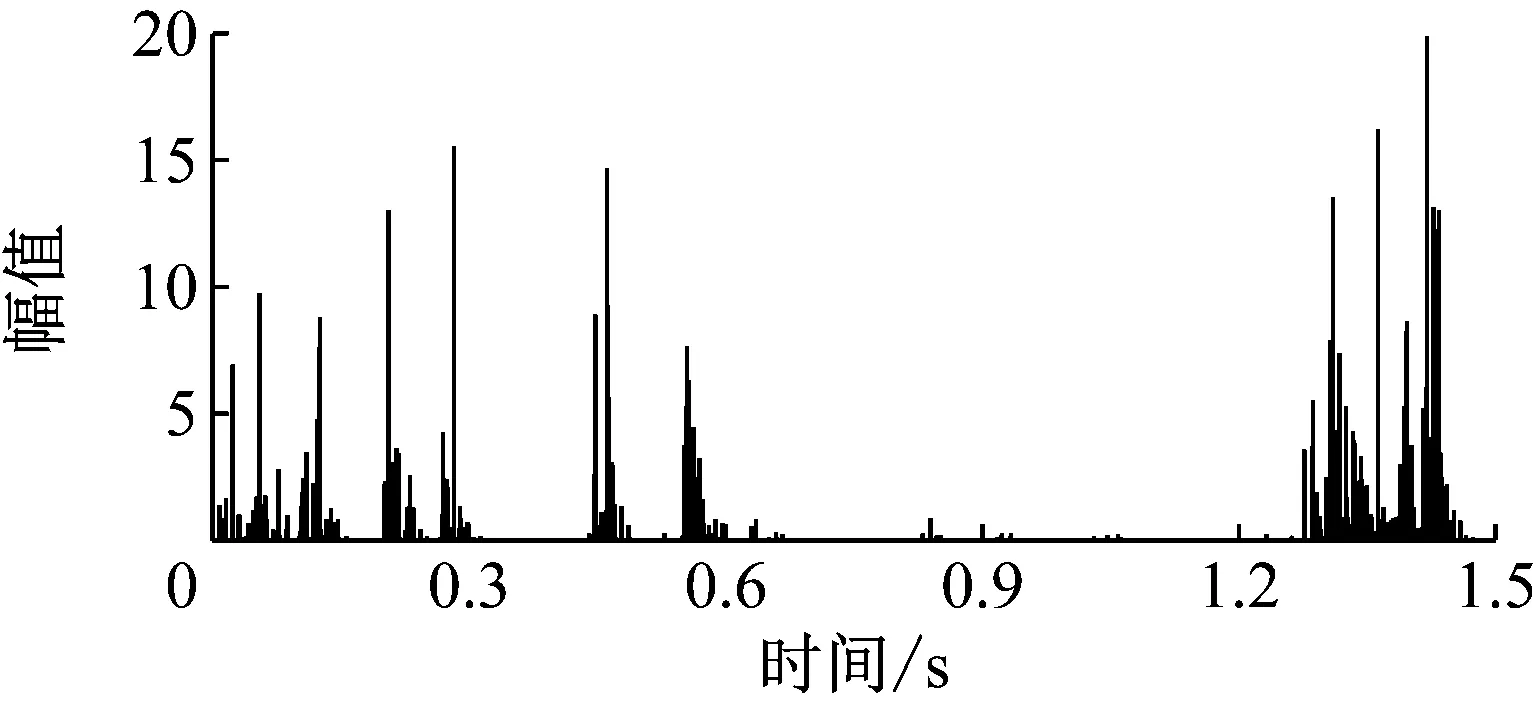
图5 时能密度曲线

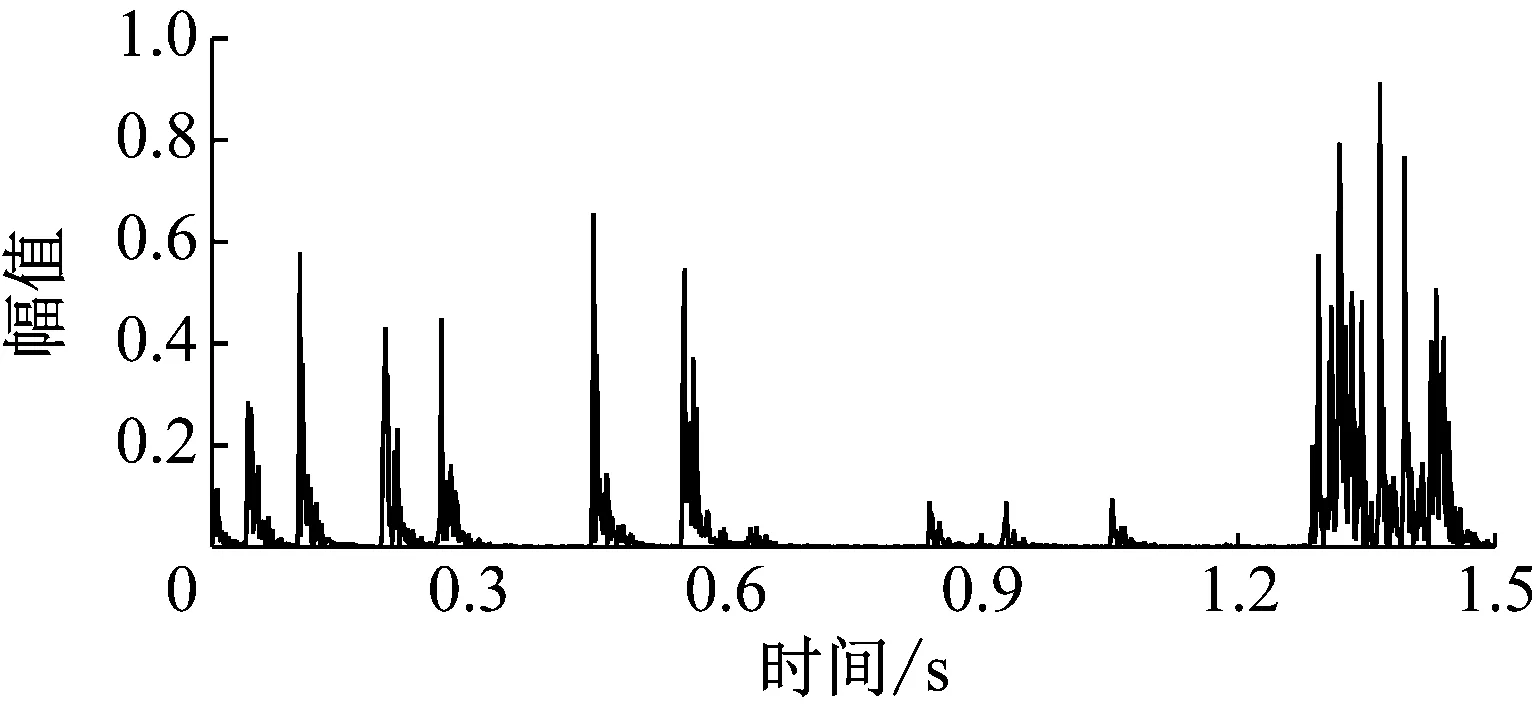
图6 小波变换模值(第三层)

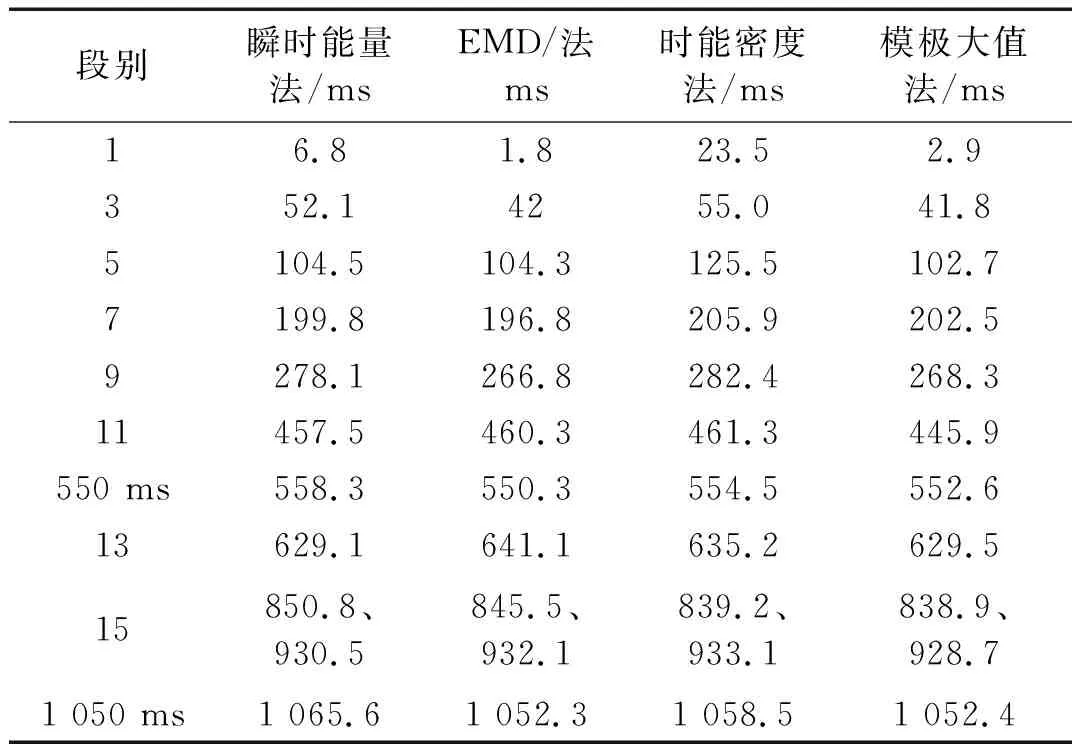
段别瞬时能量法/msEMD/法ms时能密度法/ms模极大值法/ms16.81.823.52.9 352.142 55.041.85104.5104.3125.5 102.77199.8196.8205.9 202.5 9278.1 266.8282.4 268.311457.5460.3461.3445.9550 ms558.3 550.3554.5 552.613629.1641.1635.2629.515850.8、930.5 845.5、932.1 839.2、933.1 838.9、928.71 050 ms1 065.61 052.31 058.51 052.4

3 叠加分析和频谱分析

3.1 叠加分析

现场实测波形一般是多个炮孔爆炸后各波形的叠加结果，但由于爆破振动信号非周期平稳信号，即使假设每段产生的单孔波形相同，段数不一样，相同延期时间下叠加波形的振速峰值也可能不一样。因此，利用叠加法分析延期时间和合成波形振速峰值间的关系时，有必要先消除叠加的波列数对合成波形振速峰值的影响。

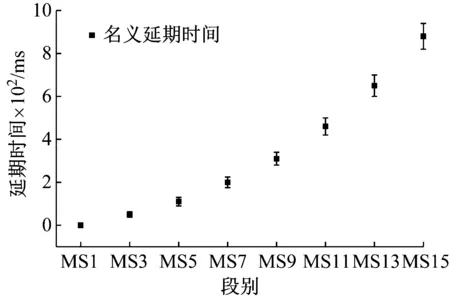
图7 非电雷管延期时间误差

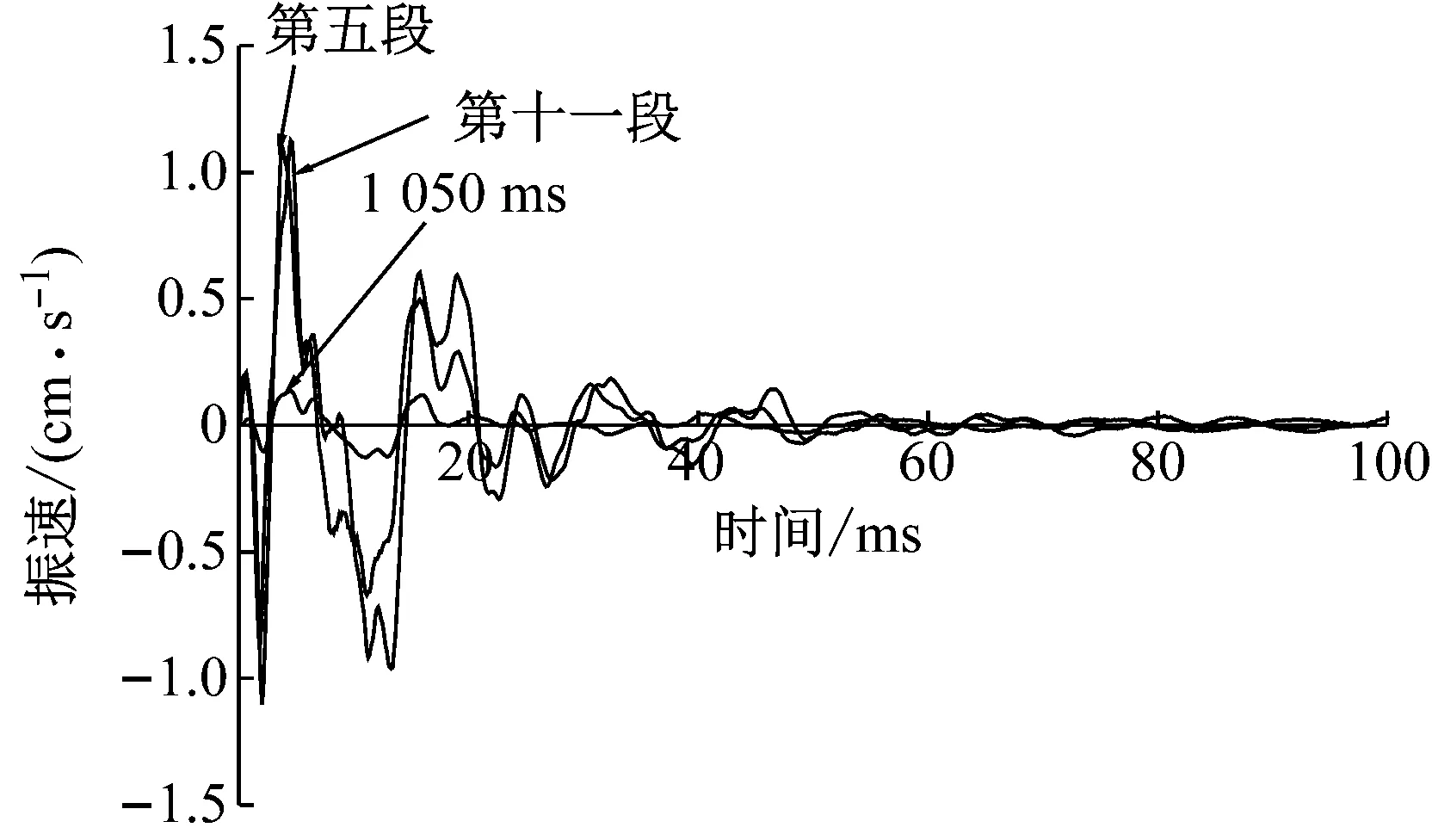
图8 各段X方向单孔波形

依据上述叠加原理，编写MATLAB程序，其中拟合级数N取300，每两列波间的延期时间为固定值T，T在区间[1,T0]上取整数值，叠加的波列数取区间[2,80]内的整数。叠加第五段单孔波形并统计任意延期时间下合成波形的振速峰值不再变化的波列数，得到图9。从图9中可以看出，不同延期时间下，当波列数达到2列后，合成波形的振速峰值不再变化的概率为0.793 81；当波列数达到15列后，合成波形的振速峰值不再变化的概率为0.986 25；当波列数为47列后，合成波形的振速峰值不再变化的概率为1。因此，当叠加的波列数为15列时，就可以不考虑波列数对合成波形振速峰值的影响，仅研究延期时间和合成波形振速峰值间的关系。

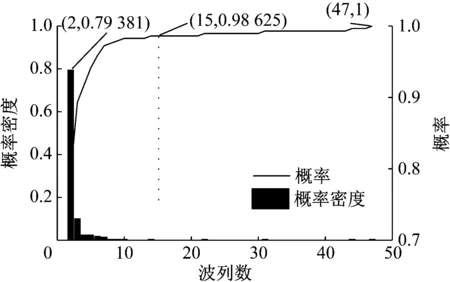
图9 大于某个波列数后合成波形振速峰值不再变化的概率

Fig.9 Probability that the peak vibration velocity of synthetic waveform will not change when the number of single waveforms is greater than a certain value

对第五段X方向单孔波形进行叠加分析，叠加结果见图10、图11、图12和图13。从图12可以看出当延期时间为17 ms时，合成波形的振动峰值首次出现最小值，振速峰值出现在合成波形中的3.75 ms处，说明合成波形的振速峰值即为第一个单孔波形的振速峰值，后续波形有所抵消。从图10和图12可以看出，当延期时间为7 ms时，合成波形振速峰值为所有峰值中的较小值，振速峰值出现在合成波形中的8.875 ms处，说明第一个波形和第二个波形有所叠加，而后期波形有所抵消。从图11和图12可以看出，当延期时间为13 ms(除1 ms)时，合成波形振速峰值为所有峰值中的最大值，振速峰值出现在合成波形中的68.75 ms处，说明后期波形有叠加增强。当延期时间大于30 ms时，合成波形的振速峰值基本为最小值。

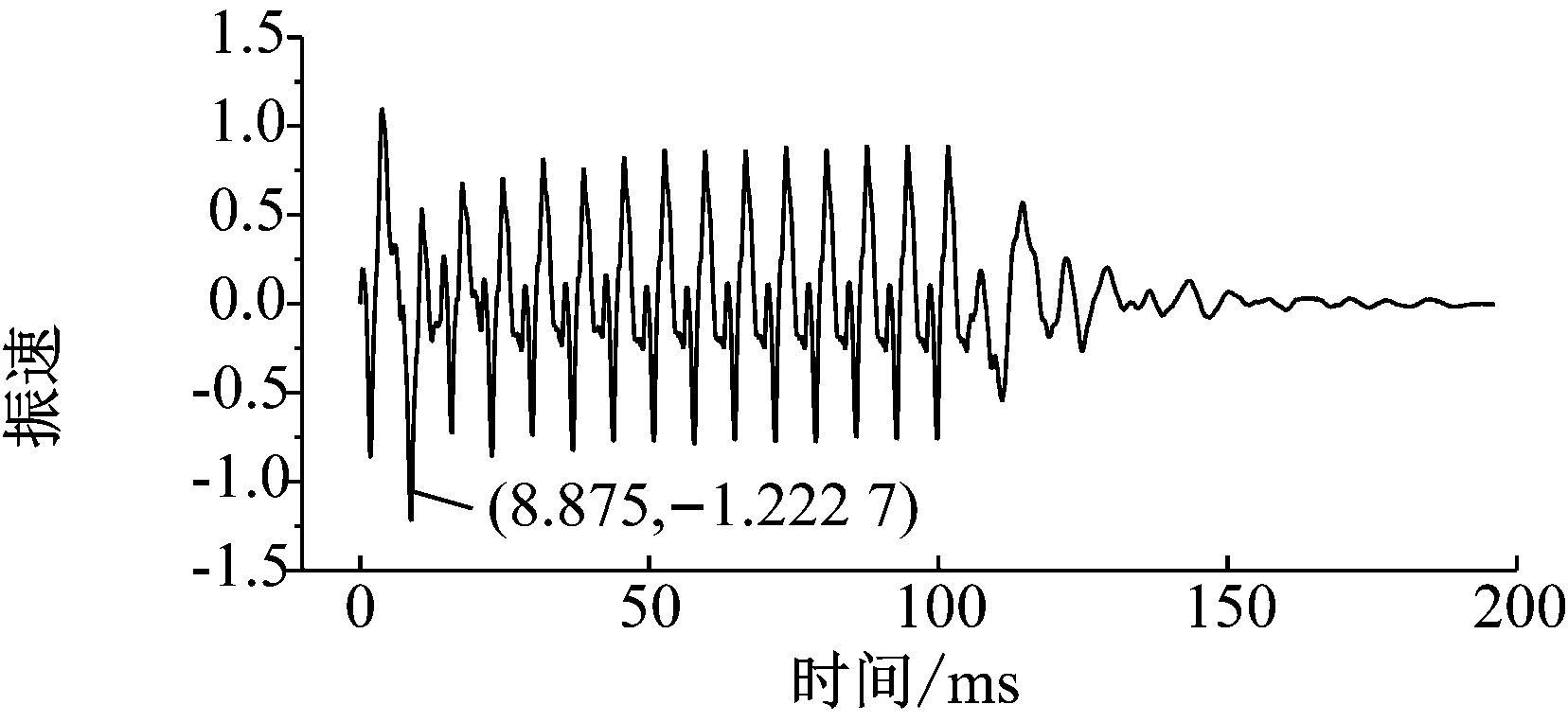
图10 第五段X方向合成波形(延期时间7 ms)

Fig.10 Synthetic waveform of fifth stage inXdirection (delay time is 7 ms)

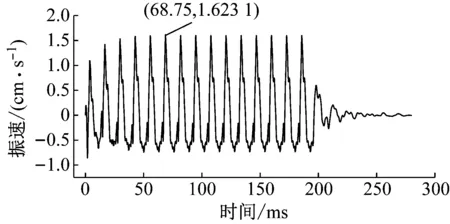
图11 第五段X方向合成波形(延期时间13 ms)

Fig.11 Synthetic waveform of fifth stage inXdirection (delay time is 13 ms)

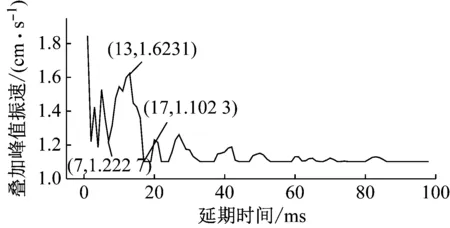
图12 第五段X方向延期时间与叠加峰值

Fig.12 Delay time and superposition peak value of fifth stage inXdirection

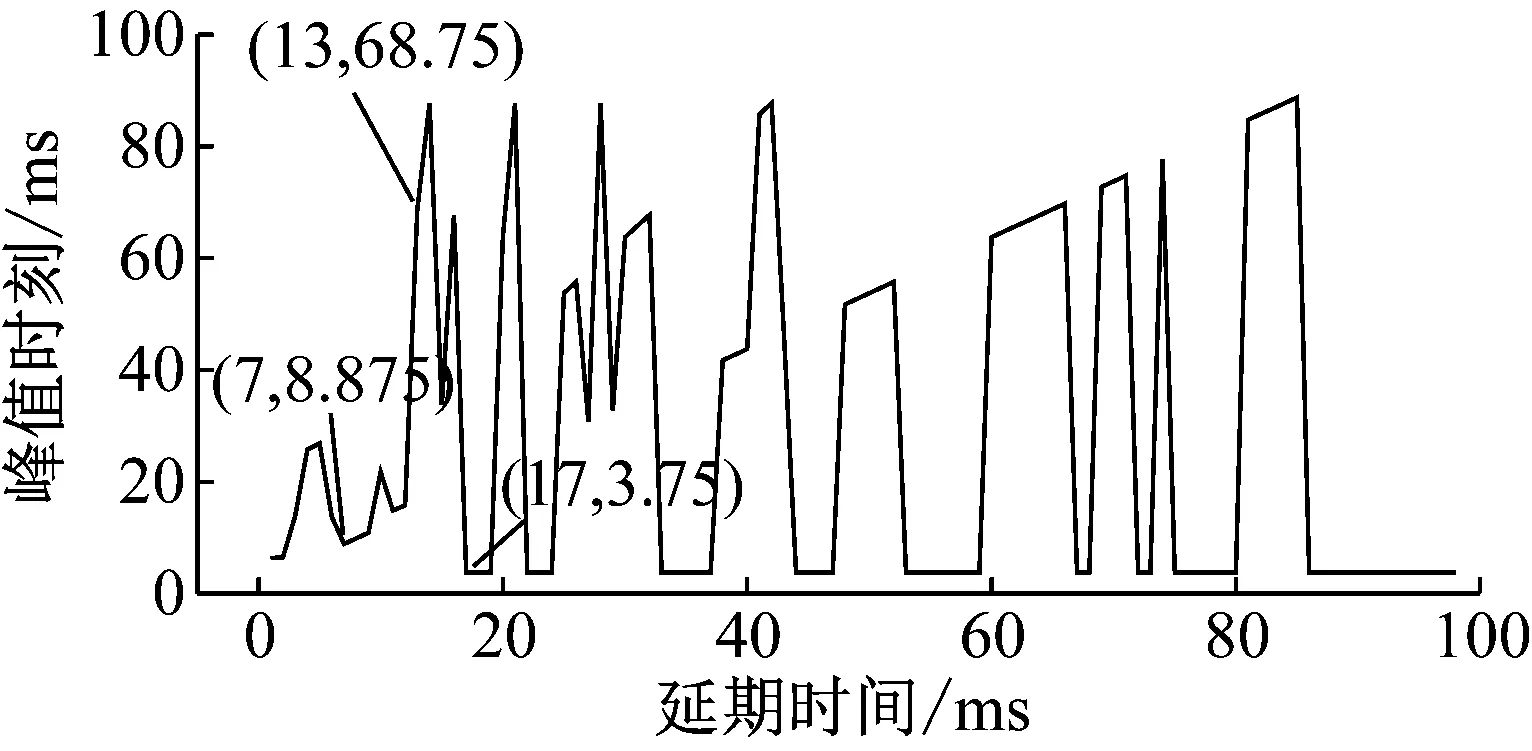
图13 第五段X方向延期时间与峰值出现时刻

Fig.13 Delay time and peak occurrence time of fifth stage inXdirection

同样的方法叠加第五段、第十一段和1 050 ms三个方向上的单孔波形，统计叠加结果于表2。从表2和图12可以看出，当15列波形叠加后，合成波形的最小峰值一般为单孔波形的峰值，出现在首个单孔波形的峰值处。而最大或较大峰值一般为多个单孔波形叠加后产生的，大于单孔波形的峰值，说明最大峰值对应的延期时间下，在一定时间内，波形有所叠加增强。从表2还可以看出，不同方向上根据叠加原理得到的最佳延期时间是不同的。所以，利用叠加原理确定雷管的最佳延期时间时，不能仅考虑一个方向单孔波形的叠加结果，而应综合考虑多个方向单孔波形的叠加结果。

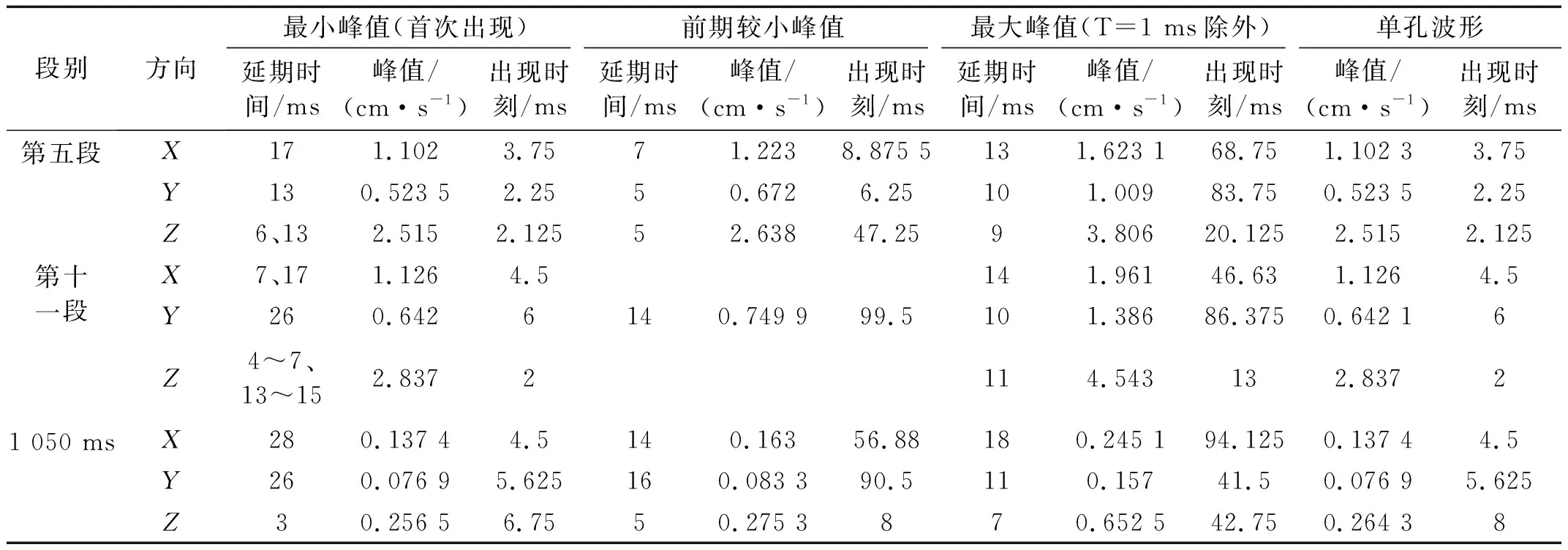
表2 各段各方向单孔波形叠加结果

3.2 频谱分析

利用快速傅里叶变换，可以将信号的时域信息和频域信息联系起来，从而可以从频域信息来考察爆破振动信号的特征。利用MATLAB编写程序，实现振动信号的快速傅里叶变换(FFT)，从而可以得到信号的频谱图。图14为第五段X方向的频谱图，从图中可以看出，第五段X方向单孔波形的主频率为78.2 Hz，即主周期为12.8 ms。对第五段、第十一段和1 050 ms不同方向上的单孔波形作快速傅里叶变换，频谱分析结果统计于表3。从表3可以看出，不同段单孔波形在同一方向上的主频基本稳定，不同方向上的主频不同。结合表2和表3，可以得到振动峰值最小、较小和最大时对应的延期时间与主周期的比值，结果见表4。从表4中可以看出，当延期时间为主周期的0.4倍～0.7倍(0.5倍左右)、1.4倍～1.7倍(1.5倍左右)和2.4倍～2.7倍(2.5倍左右)时峰值振速最小或较小，这说明错相降振是可行的，但是合成波形振速峰值最小值通常为单孔波形的振速峰值。除延期时间为1 ms的情况外，当延期时间为主周期的0.9倍～1.2倍(1倍左右)时，合成波形的振速峰值达到最大，说明此时各单孔波形叠加增强。

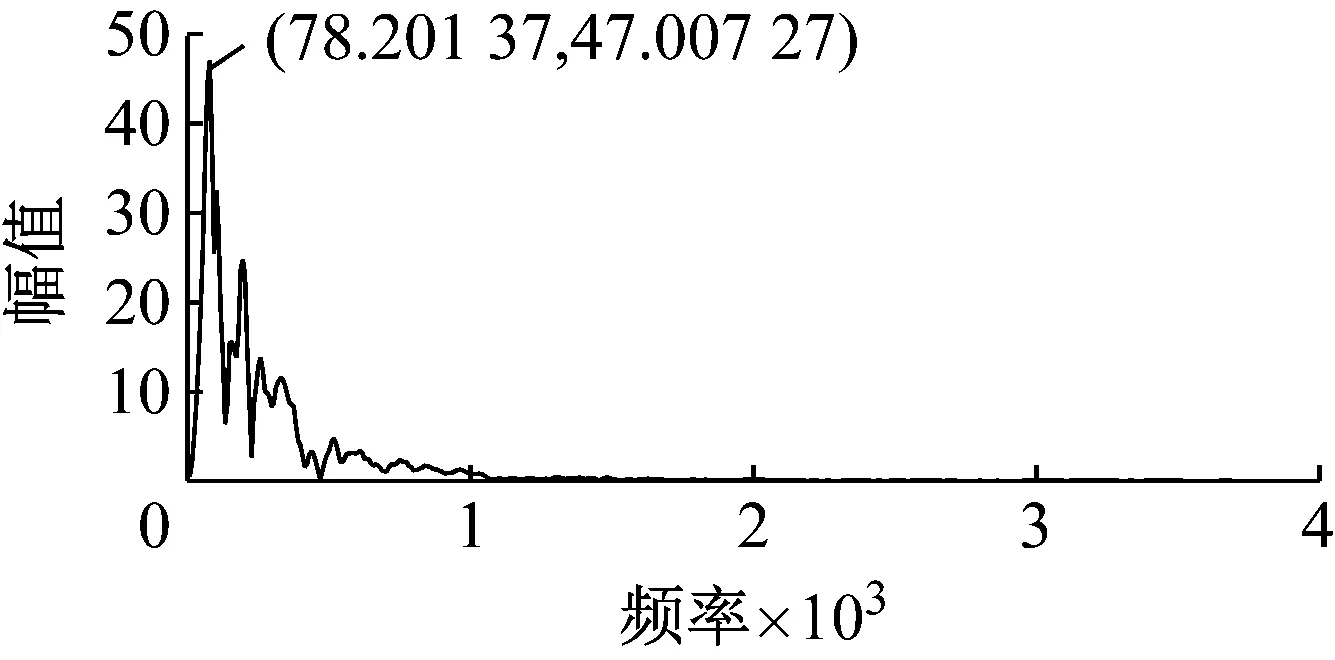
图14 第五段X方向频谱图

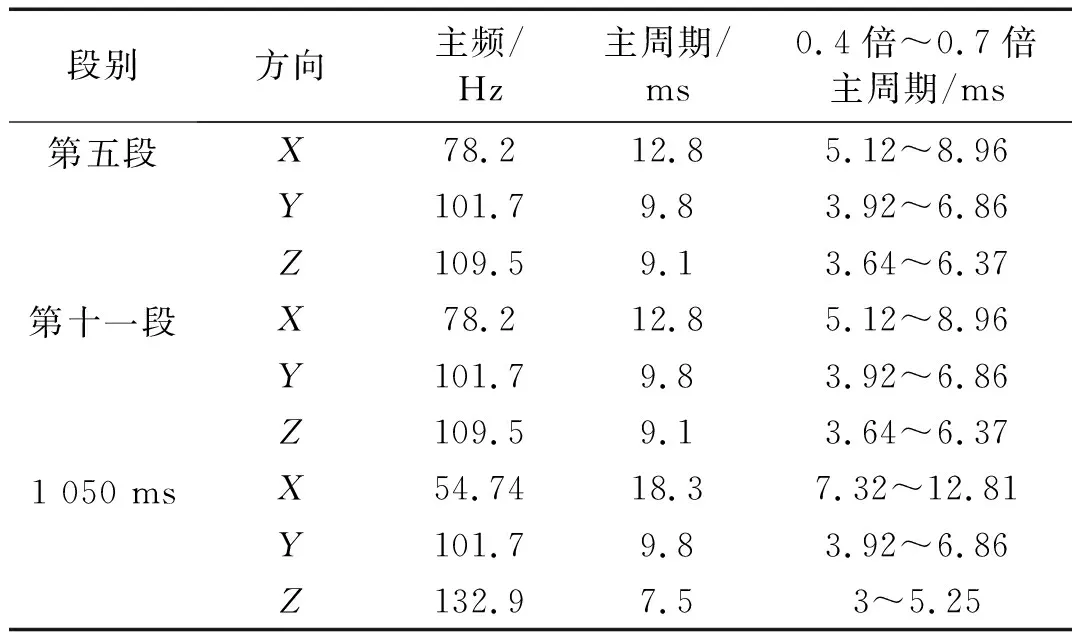
段别方向主频/Hz主周期/ms0.4倍～0.7倍主周期/ms第五段X78.212.85.12～8.96Y101.79.83.92～6.86Z109.59.13.64～6.37第十一段X78.212.85.12～8.96Y101.79.83.92～6.86Z109.59.13.64～6.371 050 msX54.7418.37.32～12.81Y101.79.83.92～6.86Z132.97.53～5.25

3.3 最佳延期时间的确定

根据上述分析，当延期时间取半个周期时并不能完全保证合成波形振速峰值最小，只能说延期时间为主周期的0.4倍～0.7倍、1.4倍～1.7倍或2.4倍～2.7倍时，合成波形振速峰值会有较小或最小值。但是当延期时间为主周期的1倍左右时，合成波形的振速峰值必然会叠加增强。为了提高减振可靠性，使合成波形振速峰值最大可能地降低，提出了如下确定最佳延期时间的方法。首先通过线性叠加原理来确定最佳延期时间，根据多个单孔波形的叠加结果，考虑主要的控制要求，得到备选延期时间。然后，根据快速傅里叶变换求出单孔波形的主周期，判断备选延期时间是否符合半周期减振原理，即备选延期时间是否为各单孔波形主周期的0.4倍～0.7倍、1.4倍～1.7倍或2.4倍～2.7倍。若符合，即得到最佳延期时间。若不符合，重新选择较优的延期时间，并重复上述步骤，直至找到最佳延期时间，这样通过两种原理相辅相成，得到更加可靠的最佳延期时间，有效地降低爆破振动。具体流程,如图15所示。

表4 相应延期时间与主周期的比值

Tab.4 The ratio of the corresponding delay time to the main period

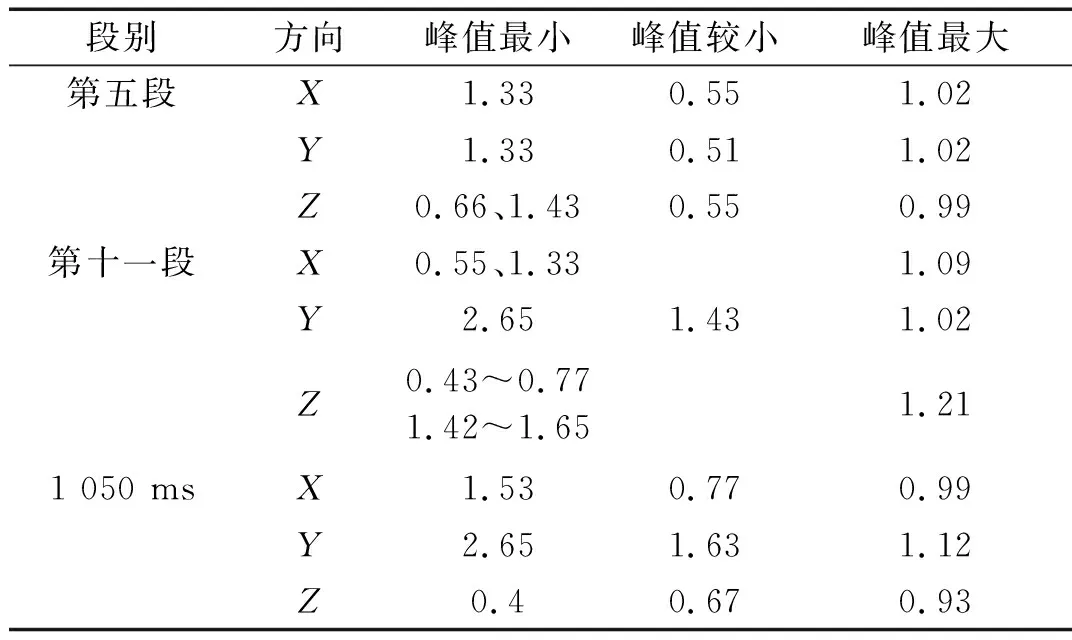
段别方向峰值最小峰值较小峰值最大第五段X1.330.551.02Y1.330.511.02Z0.66、1.430.550.99第十一段X0.55、1.331.09Y2.651.431.02Z0.43～0.771.42～1.651.211 050 msX1.530.770.99Y2.651.631.12Z0.40.670.93

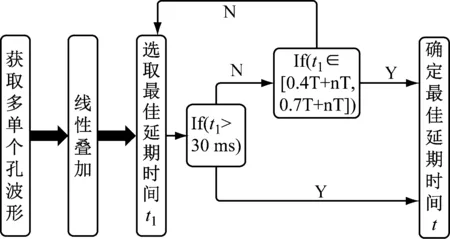
图15 最佳延期时间确定方法

本实验单孔波形主周期的0.4倍～0.7倍如表3所示。根据上述方法，为了保证爆破协同性，最终确定的最佳延期时间为6 ms，满足主要控制要求，且与各方向单孔波形主周期的比值基本为0.47～0.66，符合干扰减振原理。本次试验中以6 ms作为电子雷管延期时间，在2 m进尺爆破中，测得距离开挖轮廓线垂直距离1.8 m且水平距离3.5 m处各方向的振速不超过3 cm/s。

4 结 论

通过上述分析，可以得出以下结论：

(1) 以电子雷管起爆时刻的识别结果作为标准，可以较好地评价四种不同的起爆时刻识别方法。其中EMD法和小波变换模极大值法有很好的识别效果，但是这两种方法需要人为地选择反应信号特征的IMF主成分分量和最佳变换尺度。

(2) 合成波形振速峰值最小、较小或最大时对应的延期时间和主周期有很紧密的关系。一般延期时间为主周期的0.4倍～0.7倍、1.4倍～1.7倍和2.4倍～2.7倍时，得到的合成波形振速峰值为最小或较小，这说明错相减振是可行的。但是在叠加波形个数较多，延期时间都相同时，一般只能使合成波形的振速峰值降低为单孔波形的振速峰值。除延期时间为1 ms的情况外，当延期时间为主周期的0.9倍～1.2倍时，合成波形的振速峰值达到最大，各单孔波形叠加增强。基于上述联系，提出了一种更加可靠的电子雷管最佳延期时间确定方法。本实验根据上述方法得到的最佳延期时间为6 ms。在此延期时间下，测得在2 m进尺爆破中距离开挖轮廓线垂直距离1.8 m且水平距离3.5 m处各方向的振速不超过3 cm/s，效果较好。

(3) 同一爆破场地同一方向上单孔波形的主频基本相同，而不同方向上单孔波形的主频有所不同。