基于模糊C均值聚类和转子轴心轨迹特征的转子状态诊断

温广瑞， 陈 征， 张志芬

(1. 西安交通大学 现代设计与轴承转子系统教育部重点实验室, 西安 710049;2. 西安交通大学 机械工程学院智能仪器与监测诊断研究所，西安 710049; 3. 新疆大学 机械工程学院， 乌鲁木齐 830046)

旋转机械广泛应用于各行各业的重点关键设备，而转子是大型旋转机械的核心组件，转子设备在运行过程中，由于工作环境、负载等因素的影响，会使转子从正常状态演变为故障状态[1]，因此仅判断转子运行状态是否出现异常已无法满足当前工业生产的需求，转子运行状态评估和故障程度的预判已经成为制造服务业的迫切需求。

故障诊断的过程分为信号采集、特征提取(或数据预处理)和诊断推理三大部分。模糊理论、灰色理论[2]、DS证据理论[3]、以支持向量机为代表的多值分类器[4]、神经网络[5]等常常被用作故障诊断的推理工具，用来确定故障模式。而诊断推理方法的准确性在很大程度依赖于信号所提取特征的质量，因此选择适合的特征提取方法至关重要。对于转子振动信号而言，除了传统的时频域特征外[6]，分形理论、熵理论、小波理论、符号动力学理论、以经验模式分解为代表的信号自适应分解[7-8]、流形学习等方法在信号的特征提取领域有着广泛的应用。李兵等[9]基于数学形态学的分形维数计算方法对滚动轴承正常状态、滚动体故障、内圈故障和外圈故障信号进行了分析；曾求洪等[10]提取小波包分解后各独立频带信号分量的近似熵值作为故障特征；Lu等[11]提出了一种基于自适应多小波和综合检测指标的特征提取方法提高了对转子状态变化的敏感性；张华等[12]提出采用符号动力学信息熵结合支持向量机方法实现了液压泵故障诊断；Imaouchen等[13]应用频率加权能量算子和互补集成经验模态分解对轴承进行故障检测；同年Peng等[14]提出窄带自适应稀疏分解方法并应用到转子故障诊断，对转子常见的4种故障数据进行了分析。

转子轴心轨迹包含着转子运行最直观的信息，通过提取轴心轨迹的特征信息能够了解转子所处的状态并进行故障预警。目前国内外学者对轴心轨迹特征提取的研究分为模式识别和形态描述两大方向。用于模式识别的轴心轨迹形态学常见特征包括跳动度、轨迹半径最佳值、平均半径、散射度、凹凸度[15-16]、HU矩、傅里叶描绘子、宏观欧拉数、模糊凸凹度和边界层特征[17]、流行敏感特征[18]等。轴心轨迹形态描述方面的研究是转子运行状态评估的重要研究方向，同样有着丰硕的研究成果。王朝晖等[19]从轴心轨迹在各个象限的重合度出发，提出无量纲指标象限面积向量，定量的评价了轴心轨迹在象限内各个周期的重合度；随后王朝晖等[20]在无量纲象限面积向量的基础上通过改进面积向量法的特征计算方法，提高了识别的灵敏度。胥永刚等[21]通过扩充近似熵的定义提出了二维近似熵轴心轨迹稳定性评价；蒋林等[22]使用盒维数对旋转机械瞬时运行状态给出了定量评价；胡道达等[23]使用盒维数实现了油膜涡动、油膜振荡这两类油膜异常情况的识别。轴心轨迹的特征提取给转子状态评估提出了新的思路，其中形态描述具有很重要的应用价值，其直观可视的优势必将在工程应用中实现更大的发展。此前大多数学者仅聚焦于轴心轨迹特征的提取，而在获取特征后利用该特征进行模式识别和转子故障程度判别方面的研究较少。

本论文从描述轴心轨迹在测振面分布情况出发，提出轴心轨迹象限信息熵法，并使用模糊C均值聚类对不同程度不同故障状态的转子进行模式识别。

1 轴心轨迹象限信息熵算法

香农(Shannon)借鉴了热力学的概念，将信息中排除了冗余后的平均信息量称为“信息熵”，并给出了计算信息熵的数学表达式。

(1)

式中：pi代表某状态出现概率。

使用信息熵进行轴心轨迹特征提取的本质是将轴心轨迹在传感器布置截面空间的分布概率化，用概率去描述轴心轨迹的形貌。计算流程如下：

(1) 首先将轴心轨迹按照四个象限划分为四个区域；

(2) 对每个区域均匀划分网格，设定网格数为M×M，统计每个网格内的点出现的频率；

(3) 依据算式(2)计算轴心轨迹信息熵值Hi。

(2)

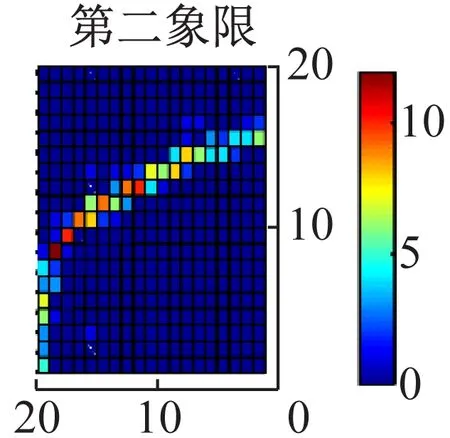
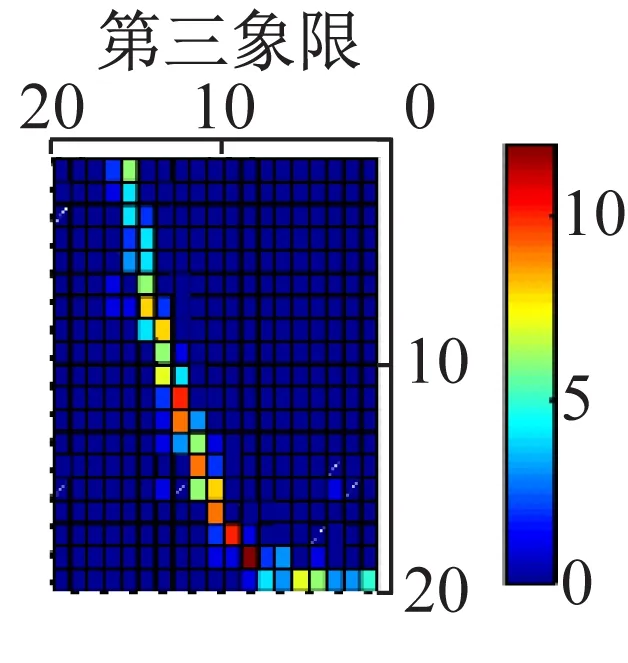
依据信息熵的定义可知，若轴心轨迹比较集中的分布在少数网格里，且在被覆盖的网格中分布比较均匀，则信息熵值较低，反之信息熵值较大。轴心轨迹象限信息熵可用来描述不同状态轴心轨迹在各个象限之间的分布情况和其在每个象限分布的均匀性，在四个象限的分布越均匀，得到的四个熵值越接近。轴心轨迹网格化过程如图1所示。算法中网格数一旦确定，轴心轨迹的边界大小就不会影响信息熵值对信息熵产生影响，对于不同尺寸的轴心轨迹，只要被网格分割的程度一致，就等同于不同轴心轨迹被限制在相同的大小，该算法仅关注每个网格内的点数而不是每个网格的尺寸，可见轴心轨迹象限信息熵是一个无量纲指标。图1中网格点颜色代表使用网格覆盖轴心轨迹后网格内点的个数。

2 基于Fuzzy C Means聚类的隶属度计算方法

1.1 FCM基本理论

聚类算法依据被分类对象对聚类中心隶属程度的取值情况可将聚类方法划分为硬聚类与软聚类两种。隶属度是表示一个对象x隶属于集合A的程度，通常记做A={(μA(xi),xi)|xi∈X}，其自变量范围是所有可能属于集合A的对象，取值范围是[0,1]。在聚类的问题中，可以把聚类生成的簇看成模糊集合，因此每个样本点隶属于簇的隶属度只能取0或1。模糊聚类方法将样本对各个类的隶属度扩展为区间连续值，表现了样本与样本之间的联系。其中最有代表性的当属模糊C均值聚类算法[24](FCM)，算法把n个向量(i=1,2,…,n)分为个模糊组，并求每组的聚类中心，使得非相似性指标的价值函数达到最小[25-27]。

FCM具体算法如下：

(1) 随机形成隶属度矩阵U，其维数为n×c，其中n为样本数，c为聚类数，随机产生U的原则如式(3)：

(3)

(2) 根据隶属度矩阵U和样本矩阵X计算聚类中心C，如(4)式所示，ci是第i类样本的中心：

(4)

(3) 依据聚类中心矩阵C计算目标函数J：

(5)

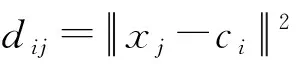
(4) 判断是否达到聚类终止条件，否则继续更新隶属度矩阵值。

(6)

FCM算法需要确定两个参数，一个是聚类中心矩阵C，另一个是参数m，它是一个控制算法的柔性的参数，m过大聚类效果会比较差，m过小则算法会接近硬聚类算法，丢失了模糊算法的优势，一般将m取为2。

2.2 模糊C均值聚类数据预处理

2.2.1 轴心轨迹网格化参数M选择

轴心轨迹象限信息熵是四维特征，为了排除转子各项异性的干扰，在研究中将四个象限的信息熵值按熵值大小排列而非四个象限的自然顺序。

依据信息熵理论可推测，过小的网格数M不足以体现不同状态轴心轨迹分布上的差异，而过大的网格数会导致不同状态轴心轨迹信息熵的趋同，不同状态轴心轨迹分布差异变小导致多个状态数据混叠，因此网格化参数M的优选很有必要。

本文提出对特征参数进行择优的流程如下：

(1) 保持尽可能大的类间距和尽可能小的类内距；

(2) 根据式(1)～(4)计算可知各个状态的类中心分布近似线性排布，类间距由各个状态类中心到正常类中心的距离和确定；

(3) 由式(5)知目标函数J由样本点到类中心的距离和依据隶属度值加权得到，则以目标函数作为类内距和的度量。

2.2.2 聚类中心C初始化

FCM中另一个关键参数聚类中心矩阵C在传统FCM算法中是从随机产生的隶属度矩阵U开始的，通过聚类中心向各个簇中心移动获取目标函数的极小值。由于目标函数是个多极值函数，随机产生的初始聚类条件会使聚类结果不稳定。因此论文使用密度估计方法进行聚类中心的初始化，改进迭代的顺序实现聚类中心矩阵C的合理初始化。具体实现方法如下：

(1) 将传统FCM算法中从初始U(隶属度矩阵)到C(聚类中心)到J(目标函数)再回到U进行循环变为从初始化C(聚类中心)到J(目标函数)到U(隶属度矩阵)再回到C(聚类中心)进行循环。

(2) 聚类初始点的初选原则是选择类内密度最大的点作为该类的初始聚类中心，如式(7)所示。

(7)

式中：n为类内样本数。

依据计算过程可知，式(6)无法使聚类中心和点集中的某个点的坐标重合，需要对搜索到的密度最大的点坐标增加一个微小的偏移量再进行聚类中心初始化，采用式(8)进行微调。FCM算法的目标函数能从任意给定的初始条件开始沿着一个迭代子序列收敛到其目标函数J的局部极小点或马鞍点，即目标函数一定会收敛。目标函数收敛标志聚类结束，聚类的解可以理解为聚类中心矩阵，目标函数往往是多极值函数，因此聚类中心矩阵也有多种可能解，目标函数收敛值和聚类中心矩阵是一一对应的关系。即偏移量的确定只要够小即可，具体取何值不会影响聚类的结果。

ci=xj+ζ

(8)

本文算法整体流程图如图2所示。

3 实验验证

3.1 实验台机方案设计

使用Bently RK4转子实验台采集数据，实验台的实物如图3所示，该实验台主要由转子系统和振动测试系统组成。转子系统包括转子，电机，轴承和基座，图中1～4分别表示电机、转轴、轴承座以及基座。振动测试系统包括六组电涡流传感器和一套连接计算机的数据采集仪。前四个传感器被分为两组，用于采集分别位于两个截面的振动信号，如图中a、b所示。第五个传感器用于测量相位，第六个传感器用于采集转速如图3中c所示。

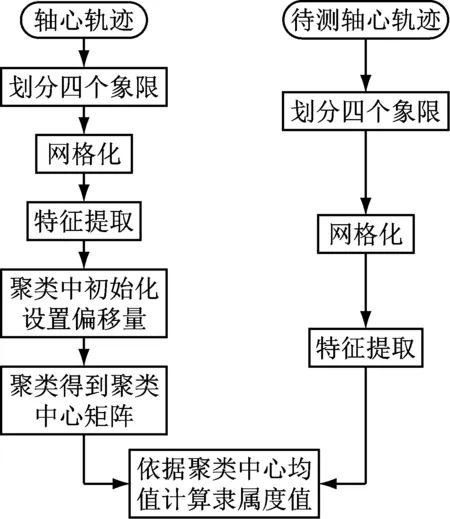
图2 算法流程图

图3 Bently RK4转子试验台

在实验台上模拟转子正常、不对中、不平衡、裂纹和碰摩五种常见转子状态，具体实现过程如图4～10。设置采样频率为1 024 Hz，采样时长为1 s，使用DT9837B数采卡对转子稳定转速过程进行连续数据采集，测量得到转子系统在4 000 r/min转速下的振动数据。

图4 轻度不平衡实验Fig.4 Mild unbalance experiment图5 重度不平衡实验Fig.5 Severe unbalance experiment

图6 轻度不对中实验Fig.6 Mild misalignment experiment图7 重度不对中实验Fig.7 Severe misalignment experiment

图8 轻度裂纹实验Fig.8 Mild cracked experiment图9 重度裂纹实验Fig.9 Severe cracked experiment

图10 轻度碰摩轴心轨迹

Fig.10 Rotor rubbing experiment

(1) 不平衡故障：在转子平衡盘的0°位置添加平衡块。轻度不平衡平衡块质量0.4 g，重度不平衡平衡块质量1.0 g。

(2)不对中故障：用垫片将图3中电机1垫起。轻度不对中使用一片垫片将电机前部垫起，重度不对中使用两片垫片将电机前部垫起。

(3) 裂纹故障：在图3中转子2中部加工裂纹。轻度裂纹深度为1/5转子直径，重度裂纹深度为1/4转子直径。

(4) 碰摩故障：使用塑料棒和图3中转子2进行碰摩。不同程度故障通过摩擦棒不同下沉深度实现。

实验得到不同程度不同故障模式振动信号，轴心轨迹分别如图11～20所示。

3.2 聚类特征向量参数 M 的确定

由于M的取值范围很大，经过尝试确定M的范围为20～50较为合适，取步长为1，计算目标函数值与类中心距离和随着网格数变化情况，计算结果如图4，以较高的类间距和较低的类内距为原则看出M=44是较为合适的网格参数。

图11 正常轴心轨迹

图12 轻度不平衡轴心轨迹

图13 重度不平衡轴心轨迹

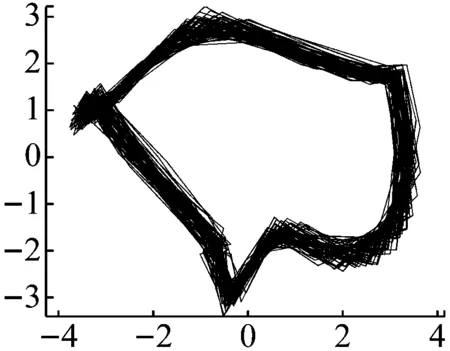
图14 轻度不对中轴心轨迹

图15 重度不对中轴心轨迹

图16 轻度裂纹轴心轨迹

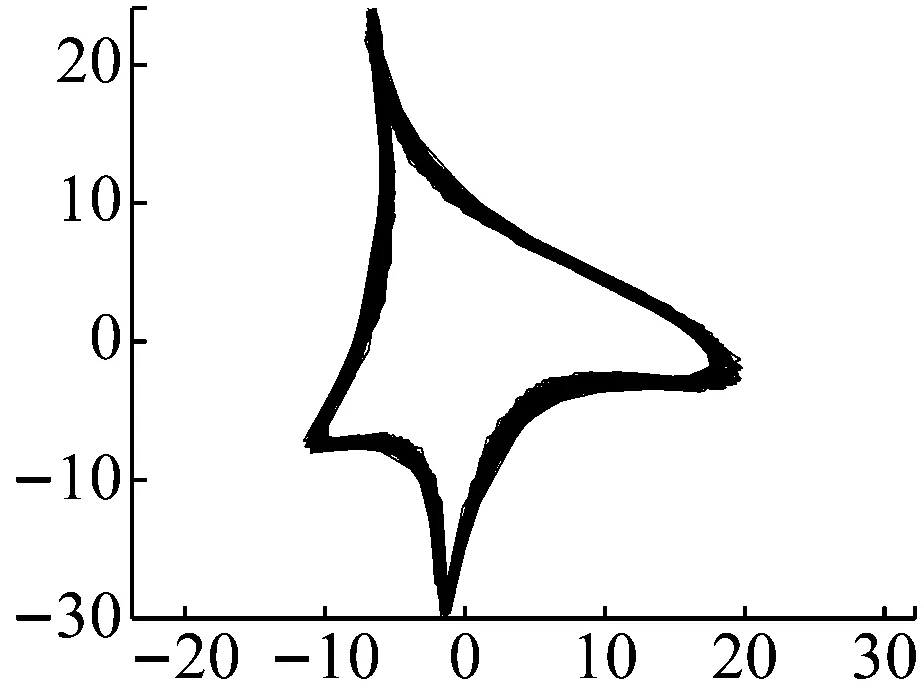
图17 重度裂纹轴心轨迹

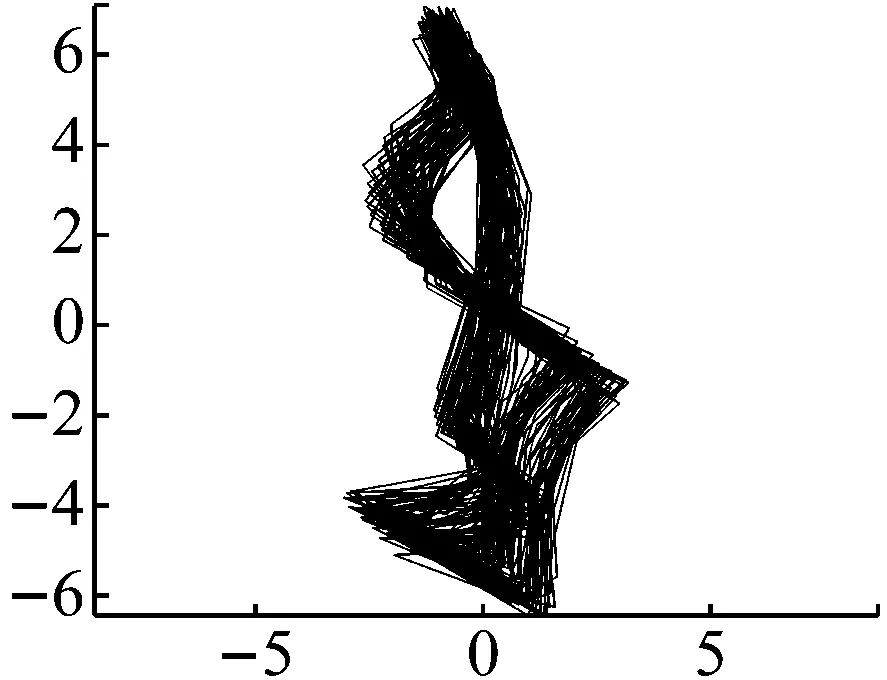
图18 轻度碰摩轴心轨迹

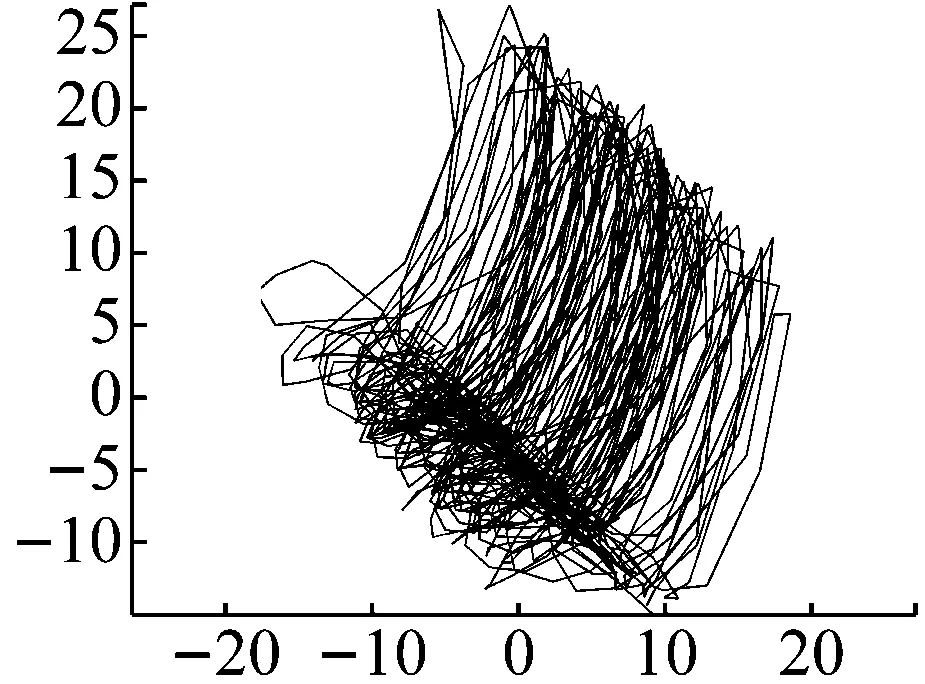
图19 重度碰摩轴心轨迹

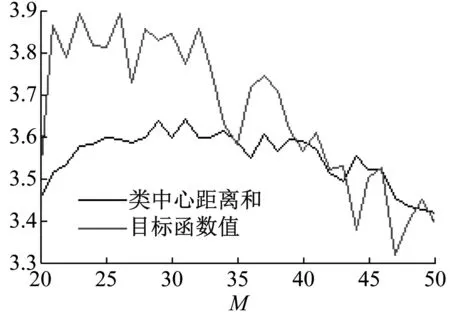
图20 目标函数值和类中心距离和随M变化

3.3 聚类中心C 初始化

使用式(7)的聚类中心初始化方法对聚类过程进行调整。图21和图22为未经过初始化多次重复计算得到的聚类结果局部图，图23是经过初始化后的聚类结果，表1为三次聚类结果目标函数值结果。

通过图21和图22可以看出，未经过聚类中心初始化的聚类结果不稳定，不同初始条件下目标函数收敛到不同值。不仅如此通过表1可以看出目标函数收敛值的高低对于聚类效果的参考价值有限，通过观察，目标函数值最低的聚类结果a错误，表明传统的FCM算法具有一定的盲目性和不稳定性，通过聚类中心的初始化可以比较好地规避这些问题。

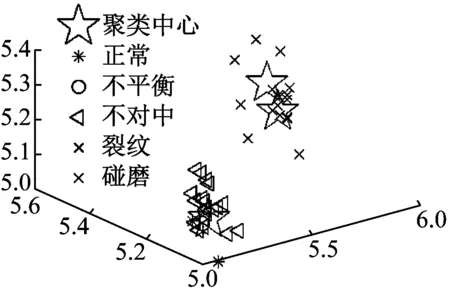
图21 未初始化聚类结果a局部图

图22 未初始化聚类结果b局部图

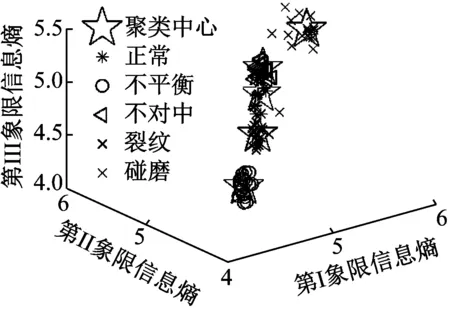
图23 初始化后聚类结果c

结果目标函数是否收敛聚类中心是否正确目标函数值a(未初始化)是否2.281b(未初始化)是否3.962c(初始化)是是3.378

此处需解释目标函数在特征参数M选择和聚类时的不同作用。首先目标函数J是样本点到各个类中心距离的加权和，通过实例看出目标函数的作用是判断聚类是否结束(J是否收敛)。对于特征参数M择优的意义在于描述类样本分布的紧密程度，因为在M变化后的每次聚类时，都需要保证聚类结果是正确的，即不能出现在一类样本中放置多个聚类中心。因此在网格数择优中目标函数值的参考意义更大。

3.4 数据验证

使用重度故障样本建立评价模型，样本总数90。使用不同程度的故障数据进行数据验证，分别为轻度不平衡，重度不平衡，轻度不对中，重度不对中，轻度裂纹，重度裂纹，轻度碰摩，重度碰摩，8种状态共40组样本，每种状态5组，依据重度故障样本构建的模型对以上8种状态进行模式识别。识别结果以隶属度值的形式展示，如图24～31所示。

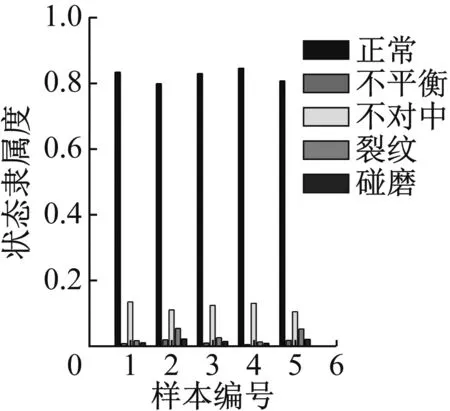
图24 轻度不平衡识别结果

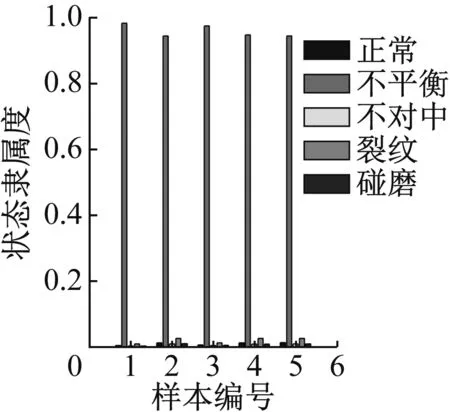
图25 重度不平衡识别结果

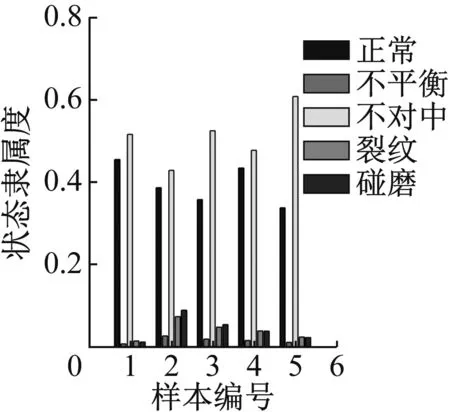
图26 轻度不对中识别结果

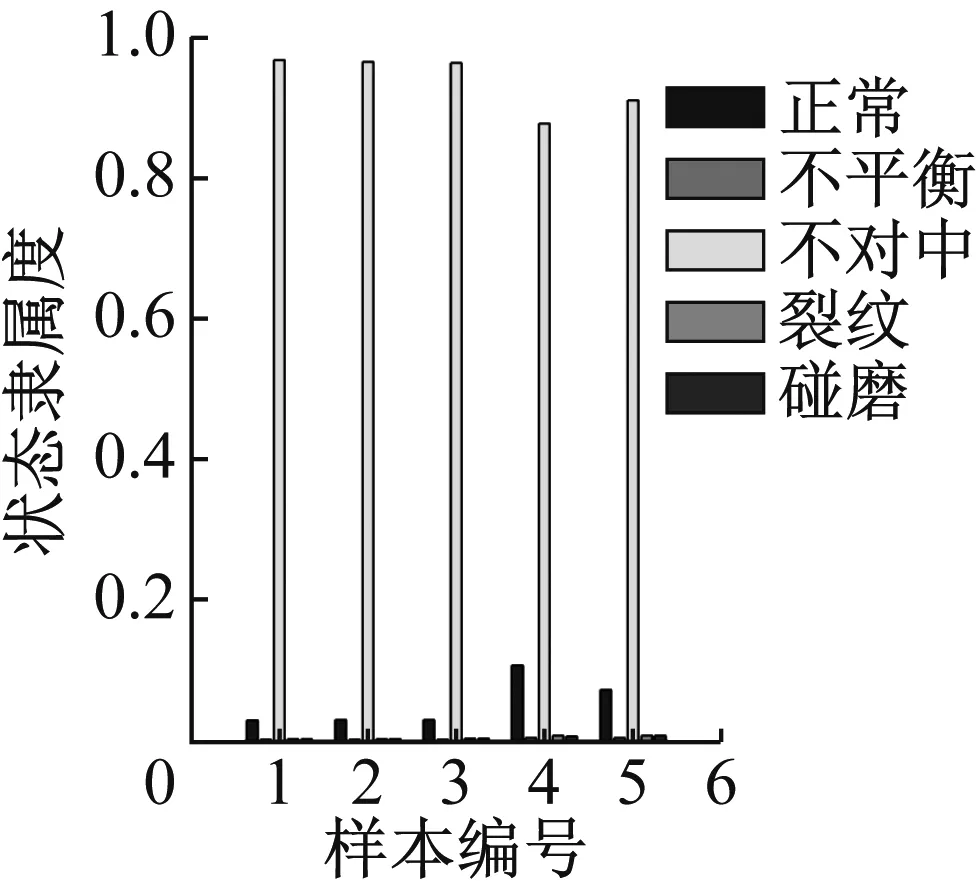
图27 重度不对中识别结果

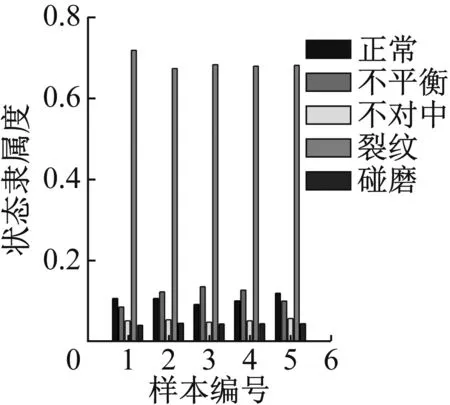
图28 轻度裂纹识别结果

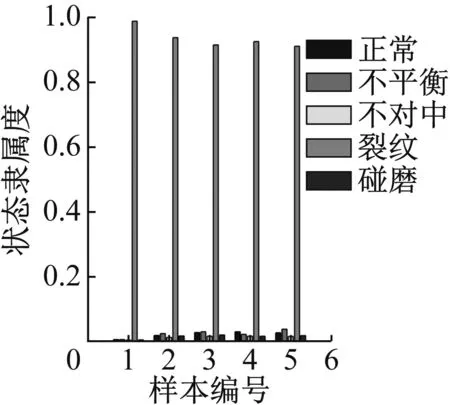
图29 重度裂纹识别结果

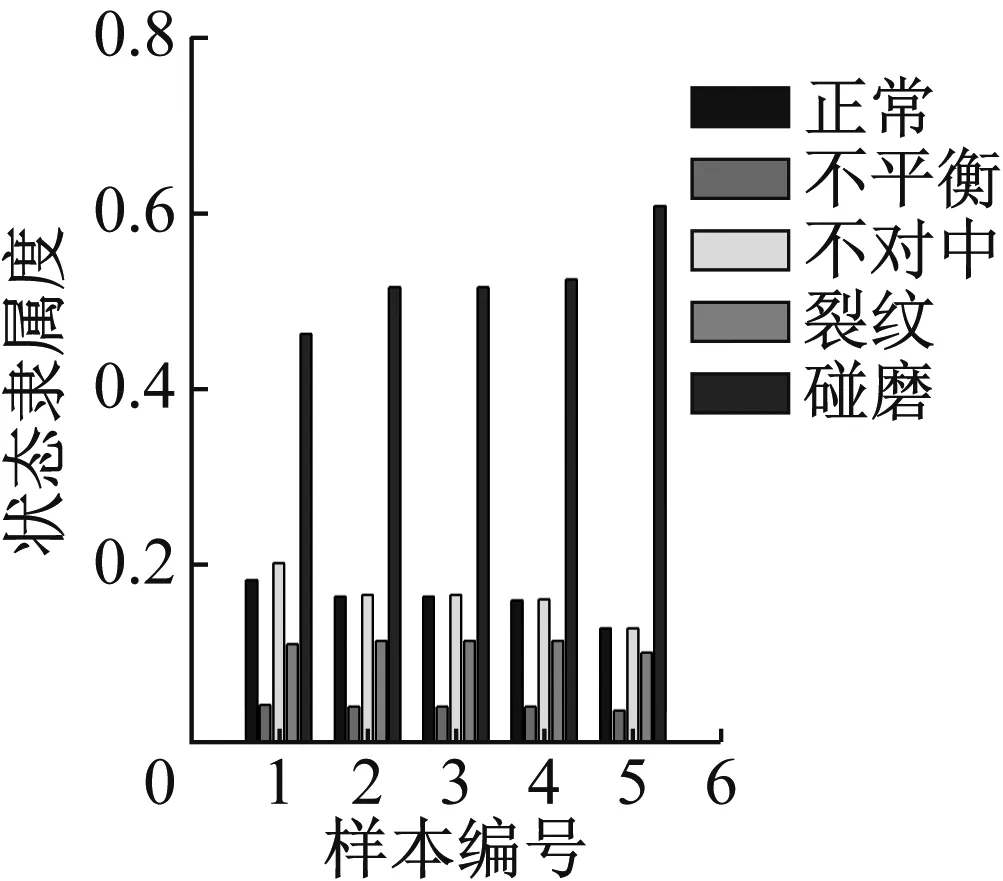
图30 轻度碰摩识别结果

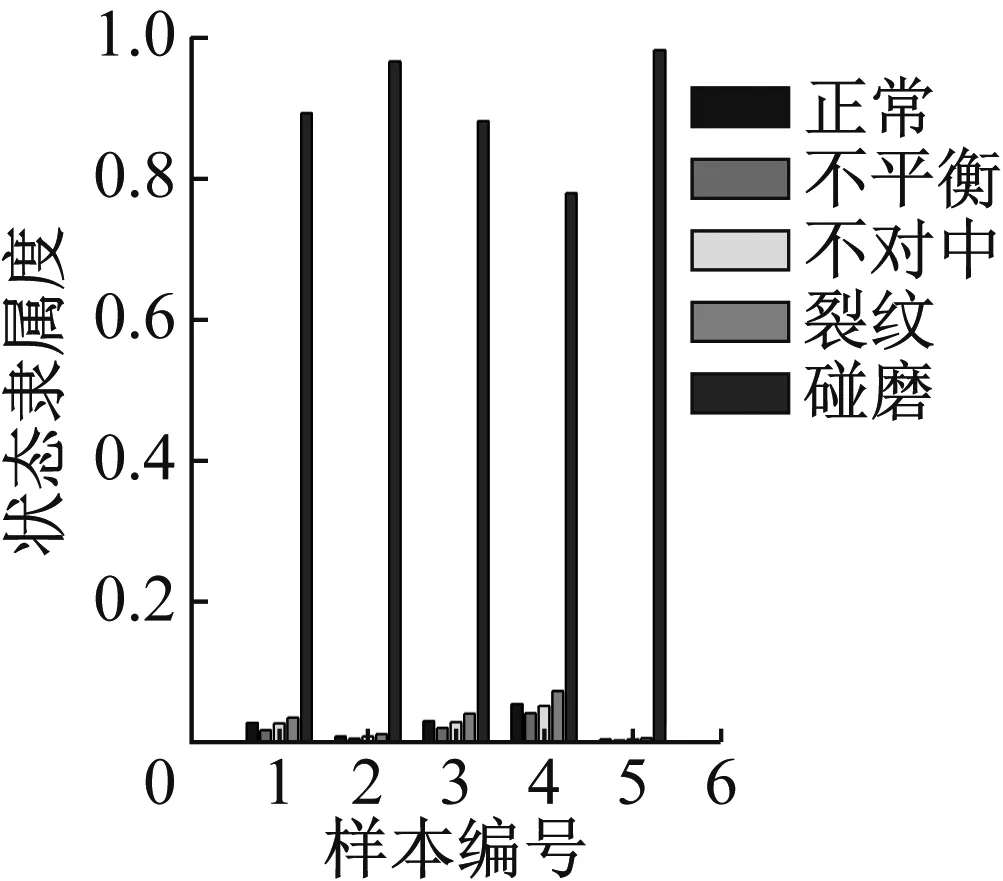
图31 重度碰摩识别结果

图24显示轻度不平衡数据对于正常有较高的隶属度，主要原因在于轻度不平衡在形态上与正常状态十分接近，可以接受。图25～31可看出其他状态的数据都可以得到较好的识别，隶属度的高低也能体现程度的高低，表明软聚类FCM算法和轴心轨迹象限信息熵指标在故障数据可视化表征上的优势。

3.5 对比验证

验证本文提出的指标，选取了3种用于轴心轨迹形态描述的指标，分别为轴心轨迹象限面积熵[19]，轴心轨迹二维近似熵[21]和轴心轨迹盒维数[22-23]，与提出指标进行对比。轴心轨迹象限面积信息熵描述了轴心轨迹在各个周期的分布均匀性和在四个象限内分布的偏心情况；二维近似熵由何正嘉于2003年提出，实现了对近似熵概念的扩充，突破近似熵仅能对一维信号进行复杂性度量的局限，使其同样适合度量轴心轨迹二维信号的复杂性，二维近似熵描述了当嵌入位数变化时，其轨迹产生新模式的概率大小，相比一维近似熵其包含更多的信息，灵敏度也更高；轴心轨迹盒维数量化的是轴心轨迹图像对空间的填充能力，评价轴心轨迹不规则程度的指标。

同轴心轨迹象限信息熵处理样本的步骤相同，建立评价模型，样本共90组。使用不同程度的故障数据进行数据验证，8种状态共40组样本，每种状态5组。识别结果如图32～39所示。

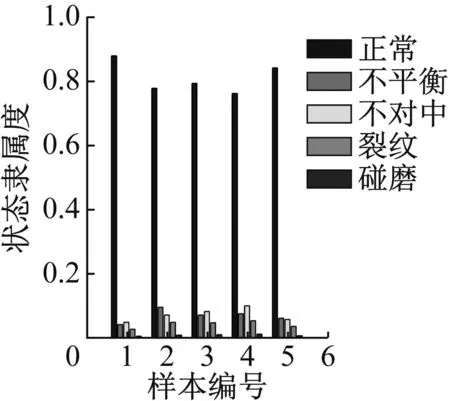
图32 轻度不平衡识别结果

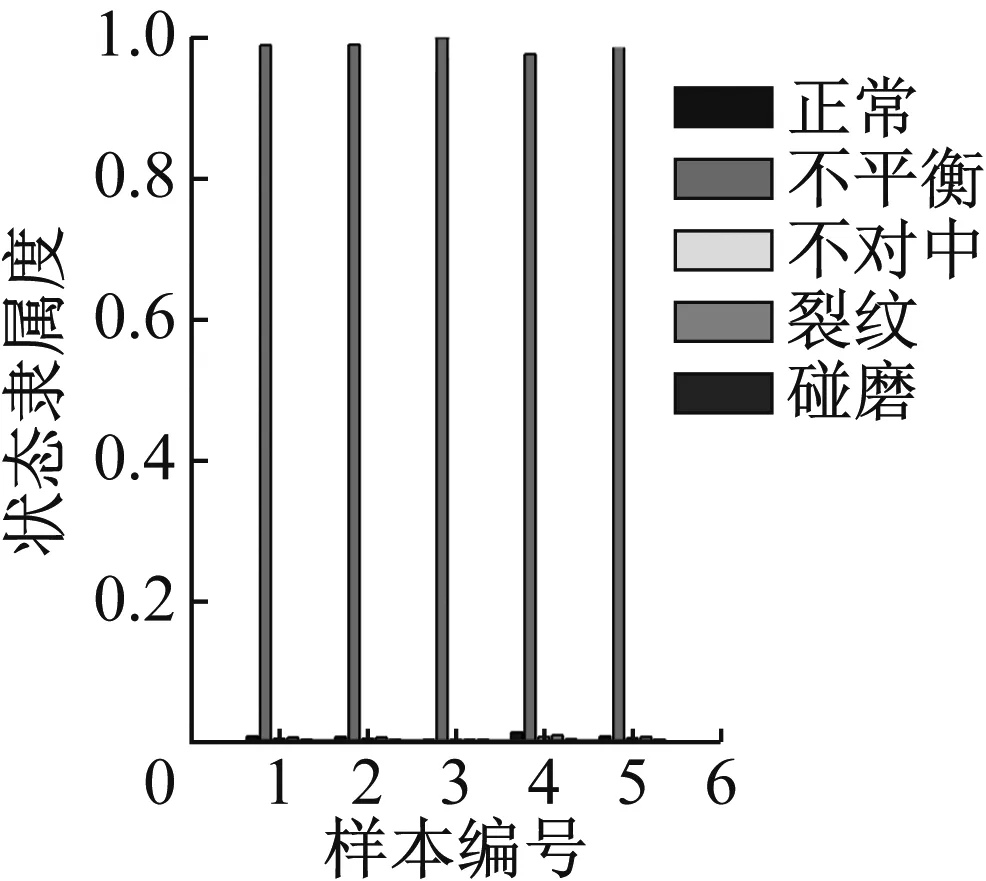
图33 重度不平衡识别结果

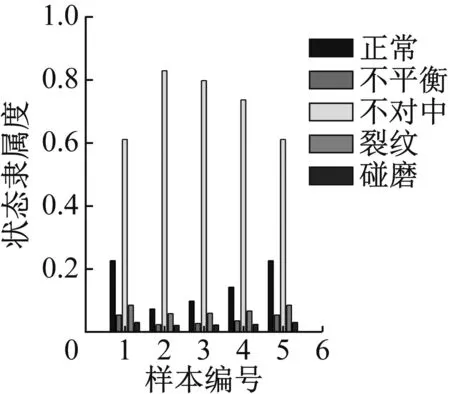
图34 轻度不对中识别结果

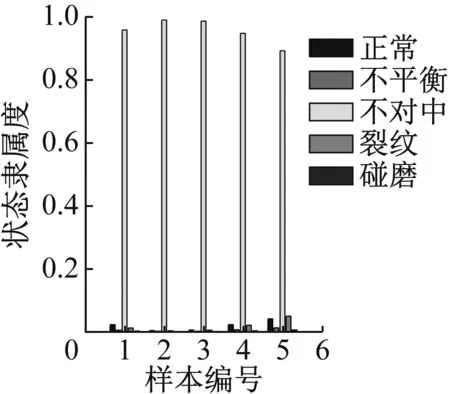
图35 重度不对中识别结果

图36 轻度裂纹识别结果

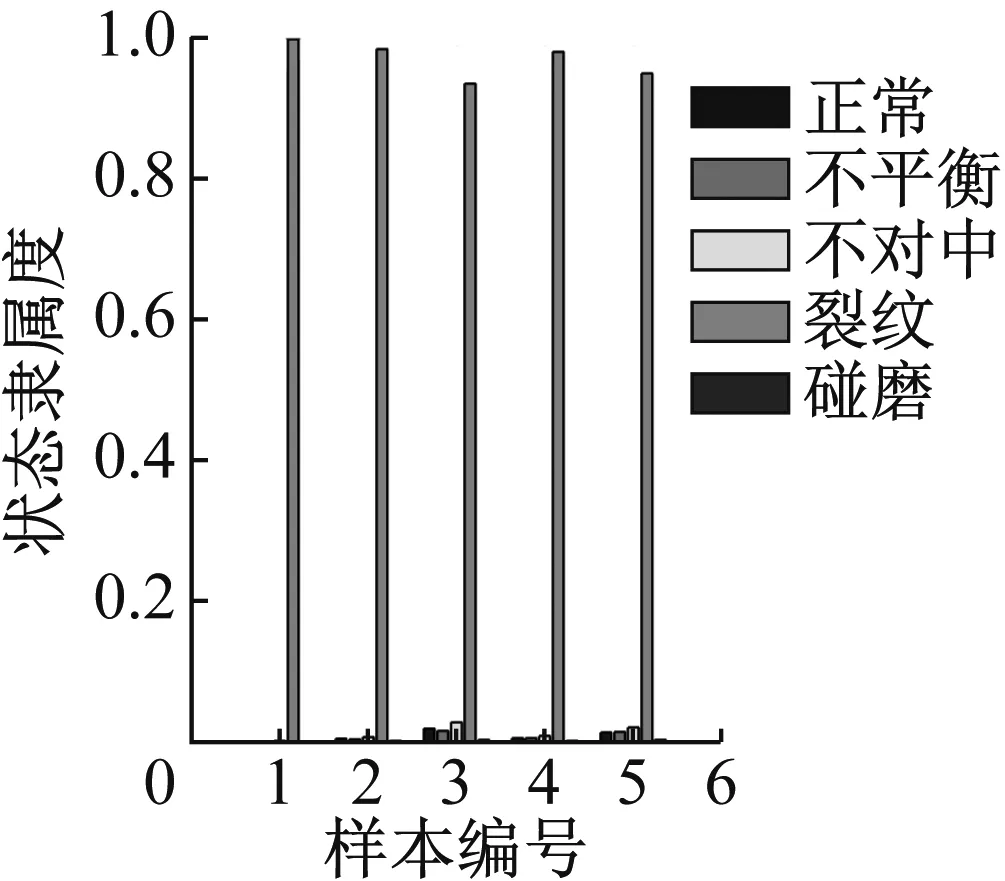
图37 重度裂纹识别结果

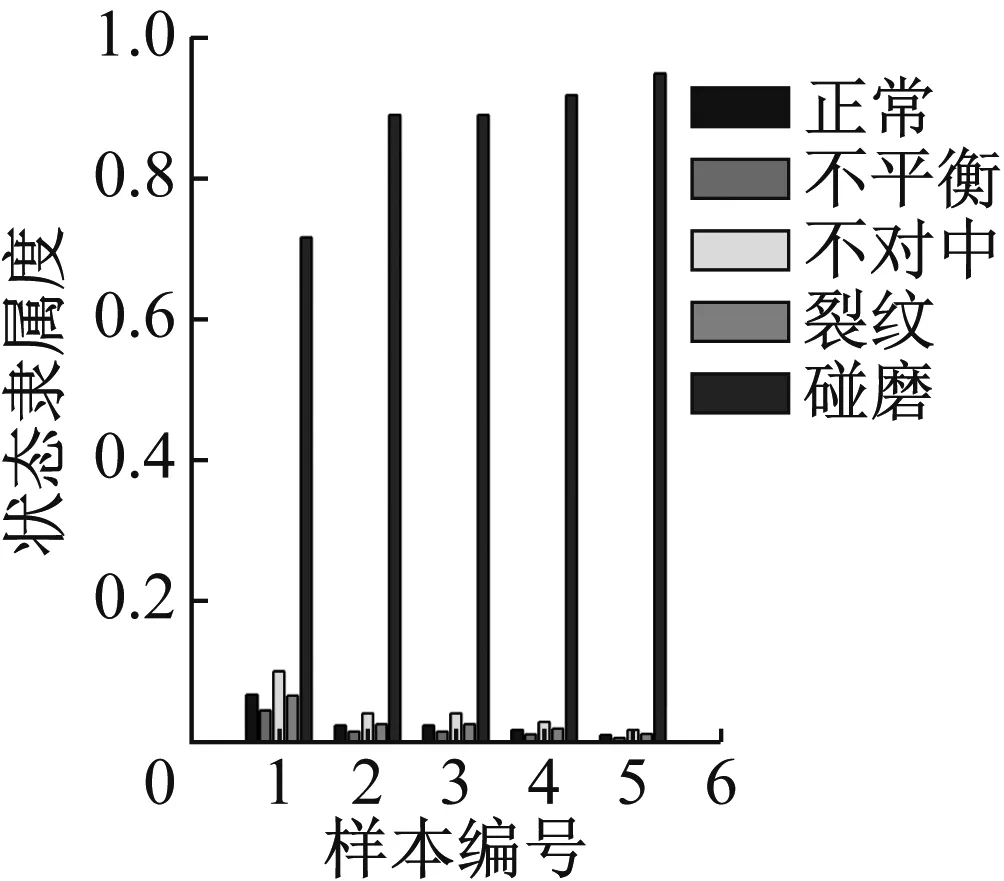
图38 轻度碰摩识别结果

通过计算结果可以看出，轴心轨迹象限面积熵，轴心轨迹二维近似熵和轴心轨迹盒维数指标，对于重度故障数据能得到比较好的识别效果，但对于轻度状态的识别结果不理想，除了不对中和碰摩之外其他故障都不能得到有效识别。

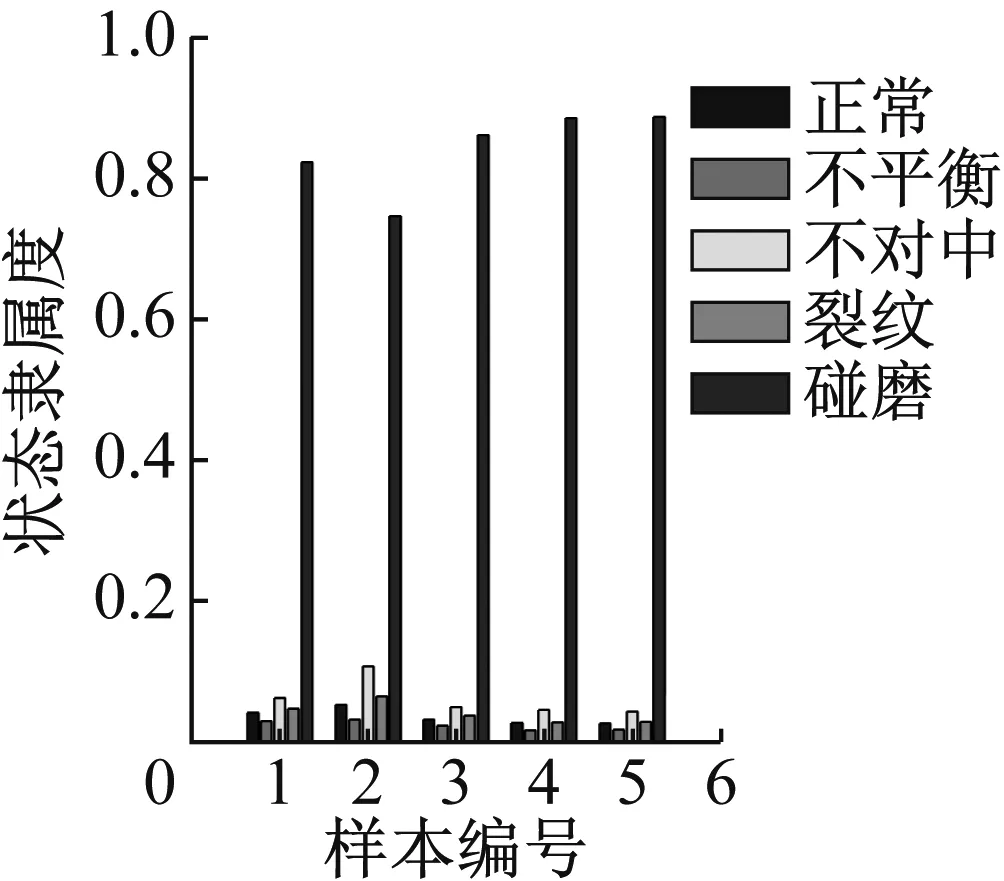
图39 重度碰摩识别结果

轴心轨迹象限信息熵评价的是轴心轨迹在四个象限的分布情况，故障程度越严重，轴心轨迹在四个象限的分布越不均匀、在单个象限的分布越离散，均会导致熵值增加，故障程度和熵值变化趋势一致。同时象限信息熵四维指标是等价的，通过指标的重排序使各个状态在聚类时其聚类中心呈类线性排列，从而可以获得了更好的识别效果。

4 结 论

本文以轴心轨迹在四个象限分布为切入点，提出了轴心轨迹象限信息熵实现转子振动信号的特征提取，得到四维信息熵特征，并以模糊C均值聚类算法作为模式识别和故障程度判别工具。通过采集不同转子故障状态的信号，讨论了网格划分程度对于聚类效果的影响，得到聚类最优网格数；通过类内密度估计初始化聚类中心提高了聚类的稳定性和成功率。

识别结果表明，以该指标建立的故障程度判别模型，对不同类型故障状态和不同程度故障状态均能有效识别。与现有轴心轨迹形态描述方法对比分析，进一步验证了本文提出的特征提取方法-轴心轨迹象限信息熵法在转子状态评估上拥有更好的状态描述和故障程度判别能力。