分布式驱动电动汽车直线行驶双模式控制

吕兵兵，严世榕，2

(1. 福州大学机械工程及自动化学院，福建 福州 350108； 2. 闽江师范高等专科学校机电工程系，福建 福州 350018)

0 引言

分布式驱动电动汽车将驱动电机直接安装在四个车轮中，每一个车轮均独立可控，只需要控制四个驱动电机就可以控制车辆的运行状态，相比于传统汽车其灵活性和可控性更高. 但是由于四个电机之间的转矩响应差异以及车辆两侧车轮所处的路面状况不同、 车辆的载荷转移等问题，在给四个驱动电机施加相同电压信号时也会出现车辆偏离直线行驶的情况. 目前，针对该问题的解决方法主要有两个： 一个是对同种规格电机的稳态误差和动态误差采取相应的控制手段, 使其转矩响应保持一致以达到车辆直线行驶[1]； 另一个是从整车角度出发，不管车辆处于何种路面、 是否出现载荷转移和是否有电机差异，通过附加横摆力矩的再分配使相应的电机进行驱动或制动来使车辆保持直线行驶，前者适应性差、 后者适应性强，但是控制模式和控制变量单一[2-3]. 本研究在以横摆角为控制变量的基础上增加车辆的侧向位移，利用二者进行联合控制，针对车辆处于不同工况下的受力特点及不同控制器的控制特点设计双模式控制器, 并在对开路面和有侧向风的工况中对车辆进行仿真验证.

1 动力学模型

1.1 车辆动力学模型

选用动力学软件CarSim搭建车辆各系统的数学模型，包括车身模型、 悬架模型、 转向模型、 制动模型、 驾驶员模型、 路面模型、 侧向风模型等[4]； 选用Matlab/Simulink搭建异步电机模型及控制系统模型. 最后，利用两者进行联合仿真.

1.2 车辆线性二自由度模型

车辆线性二自由度模型可以很好地反映出车辆的侧向位移和在不同输入参数下横摆角的变化. 由该模型计算出整车所需的附加横摆力矩ΔMz.

车辆线性二自由度方程[5]如下：

(1)

(2)

由于是直线行驶，因此δf=0. 式中：β为车辆质心侧偏角；ωr为车辆横摆角速度；y为车辆侧向位移；a、b为质心到前轴和后轴到的距离；k1、k2为前轮和后轮轮胎侧偏刚度；u为车速；δf为前轮转角；Iz为车辆绕z轴的转动惯量；m为车辆质量.

1.3 电机数学模型

轮毂电机采用结构简单、 坚固耐用的三相交流异步电动机，利用转子定向的矢量控制方法进行调速控制. 异步电机在同步旋转坐标下的数学模型[6]如下所示.

电压方程：

(3)

磁链方程：

(4)

转矩方程：

Te=pnLm(isqird-isdirq)

(5)

式中：usd、usq、urd、urq为d、q轴上的定子电压和转子电压；isd、isq、ird、isq为d、q轴上的定子电流和转子电流；Rs、Rr为定子电阻和转子电阻；Ls、Lr、Lm为定子电感、 转子电感和互感；ωs、ωs1为定子角速度和转差角频率；ψsd、ψsq、ψrd、ψrq为d、q轴上的定子磁链和转子磁链；Te为电磁转矩；p为微分算子；pn为极对数.

在按转子磁场定向时，使转子磁链ψr与d轴重合，电机转矩Te与q轴重合. 此时，可以对d轴的磁通分量和q轴的转矩分量进行单独控制，使原电机模型大大简化. 当转子磁链ψr确定时，电磁转矩Te就只与isq有关，转子磁链ψr只与电流的励磁分量isd有关，此时即可等效为直流电机模型进行高效控制[7]，矢量控制框图如图1所示.

图1 异步电机矢量控制框图Fig.1 Vector control block diagram of asynchronous motor

2 控制系统设计

在以车辆横摆角作为主控制变量的基础上，增加车辆侧向位移作为辅助控制变量，分别以车辆横摆角和车辆侧向位移设计对应的控制器.

2.1 单变量横摆角终端滑模控制器设计

设滑模切换面为：

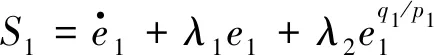
(6)

采用新型趋近率：

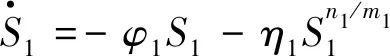
(7)

式中：λ1、λ2、φ1、η1、n1、m1均为正数，且n1、m1为正奇数.

(8)

对式(8)求导，得：

(9)

将式(2)代入式(9)，得：

(10)

令式(7)=式(10)，则：

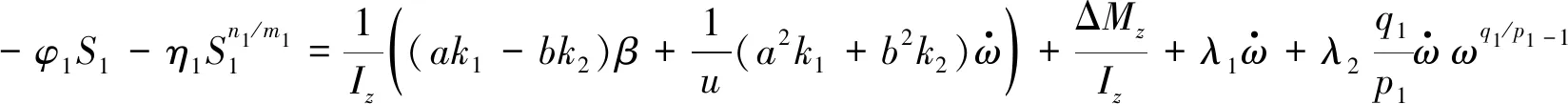
(11)

则有：

(12)

2.2 单变量侧向位移终端滑模控制器设计

设滑模切面为：

(13)

采用新型趋近率：

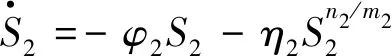
(14)

式中：λ3、λ4、φ2、η2、n2、m2都为正数，且n2、m2为正奇数.

(15)

同理，可求出：

2.3 加权系数设计

由于车辆的横摆角和侧向位移都可以反映车辆直线行驶状态，当只对其中一个变量进行控制时效果并不是很理想. 为得到更好的控制效果引入加权系数Γ，当侧向位移较小时，优先控制车辆的侧向位移； 当侧向位移较大时，优先控制车辆的横摆角.

定义加权系数为Γ[8]：

(17)

则最后总的附加横摆力矩ΔMz为：

ΔMz=ΓΔMzy+(1-Γ)ΔMzω

(18)

2.4 模糊控制器的设计

模糊控制器的输入变量为车辆实际横摆角与理论横摆角间的误差E及误差变化率EC，输出变量同样为附加横摆力ΔMz，ΔMz转换为车轮驱动力矩ΔTtire，有ΔTtire=ΔMzR/B. 设E和EC的模糊论域为[-2 2]，ΔMz的模糊论域为[-1 1].E、 EC和ΔMz都选定5个模糊子集，分别为{PB，PS，Z，NS，NB}，依次表示正大，正小，零，负小，负大，并采用三角隶属函数，然后制定相应的模糊规则，如图2～3和表1所示.

图2 E、 EC的隶属函数Fig.2 Membership function of E and EC

图3 ΔMz的隶属函数Fig.3 Membership function of ΔMz

表1 模糊规则

3 仿真验证

利用CarSim和Matlab/Simulink建立联合仿真平台，方向盘转角为0°，路面为对开路面，仿真时间30 s. 其它参数为a=1.139 06 m，b=1.637 16 m，m=1 529.98 kg，B=1.55 m，R=0.325 m.

3.1 低速无侧向风试验

设置车速为45 km·h-1，路面为对开路面，附着系数分别为0.2和0.85，侧向风为0 km·h-1，仿真时间30 s，仿真结果如图4～5所示. 图4中包含无控制、 单变量横摆角终端滑模变结构控制、 横摆角模糊控制、 双变量联合终端滑模变结构控制，而图5为图4中三种控制方法的控制效果对比图.

图4 车辆横摆角(v=45 km·h-1)Fig.4 Yaw angle of vehicle(v=45 km·h-1)

图5 控制效果对比图(v=45 km·h-1)Fig.5 Control effect comparison diagram(v=45 km·h-1)

此时，侧向风为零，车辆的受力较为简单，双模式控制系统切换为带有加权比重的侧向位移和横摆角联合终端滑模变结构控制模式. 由于车辆两侧车轮所处的路面附着系数不同即路面种类不同，导致车辆右侧车轮的驱动力大于左侧车轮的驱动力使车辆产生一个围绕z轴逆时针旋转的横摆力矩，车辆偏离直线向左边行驶. 从图4中可以看出经过单变量控制器、 联合控制器控制之后车辆都可以保持直线行驶，但图5显示联合控制模式比单变量控制模式效果更好、 精度更高，并且好于横摆角模糊控制.

3.2 高速有侧向风试验

设置车速为120 km·h-1，在车辆行驶10 s时施加侧向风，风速为50 km·h-1，风向-90°，持续20 s，路面附着系数为0.85，仿真时间30 s，仿真结果如图6～7所示. 图6中包括无控制、 单变量侧向位移终端滑模控制、 双模式控制(切换为横摆角模糊控制)，而图7为图6中三种控制方法的控制效果对比图.

此时，因有侧向风干扰且车速高, 车辆受力复杂，侧向风会使车辆沿x、y、z轴产生3个平动及3个转动[9]，导致车辆严重偏离直线行驶轨迹. 若仍沿用前面的控制方法则控制精度变差，大大降低车辆安全性，所以, 此时宜将双模式控制切换为横摆角模糊控制，模糊控制对无法建立精确数学模型的系统具有很强的鲁棒性. 从仿真结果图6中可见，三种控制方法均可抑制车辆的偏向行驶，但是从图7中同样可以发现, 双模式控制器切换为横摆角模糊控制时的效果比双变量联合终端滑模变结构控制要好得多.

图6 车辆横摆角(v=120 km·h-1)Fig.6 Yaw angle of vehicle(v=120 km·h-1)

图7 控制效果对比图(v=120 km·h-1)Fig.7 Control effect comparison diagram(v=120 km·h-1)

4 结语

在以往的控制策略基础上针对其不足之处，根据车辆在不同行驶工况下的受力特点和不同控制器的控制特点，制定了整车双模式控制策略. 相对于传统的单一控制变量和单一控制模式，该策略控制精度更高、 效果更好且适应性更广，极大地提高了车辆的行驶安全性和轨迹跟随能力.