以第一性原理研究单层二硫化钼压电特性
许 婧, 罗 静, 李明林
(1. 福州大学机械工程及自动化学院, 福建 福州 350108; 2. 厦门钨业股份有限公司,福建 厦门 361000)
0 引言
单层二硫化钼是近年来备受关注的二维纳米材料中的一员,具有优异的电学、 光学、 催化和固体润滑性能[1]. 不同于零带隙的石墨烯,单层二硫化钼是具有约1.8 eV禁带宽度的直接带隙半导体材料[2],这使其在纳米电子器件、 光电子器件等领域具有潜在的广泛应用前景[3-6].
近期研究显示,单层二硫化钼还具有优良的压电效应,可用于传感器、 能量收集器等[7]. 在实验研究方面,Qi等[8]研究了机械变形下单层MoS2器件的压电效应,发现应变极化诱导的内电场可有效调节器件的导电性. Wu等[9]发现只有奇数层二硫化钼才具有压电效应. Zhu等[10]实验测得单层二硫化钼压电系数e11为(0.29±0.05)nC·m-1. 在理论研究方面,Zhou等[11]采用有限元方法对Wu等[9]的实验研究进行理论分析,验证了二硫化钼压电特性的层数效应. 文[12-17]则使用PBE泛函研究了包括二硫化钼在内的材料的压电特性、 弹性常数的特性. 此外,文献中也有采用其他交换关联泛函计算二硫化钼物理特性的研究. 杨志鹏等[18]采用LDA计算了二硫化钼的光学性质,而文[19]则利用PW91赝势探讨了硫空位缺陷扶手型二硫化钼纳米带的结构与电子性质. 由于材料压电特性涉及材料的力学特性和电特性,据笔者所知,尚未有文献报道采用不同交换关联泛函研究二硫化钼的压电特性.
本研究基于密度泛函理论的第一性原理,分别采用GGA(generalized gradient approximation)[20]和LDA(local density approximation)[21]两种近似方法计算单层二硫化钼的晶格结构参数、 能带、 弹性常数和压电系数,其中GGA主要采用PW91和PBE两种交换关联泛函.
1 模型及方法
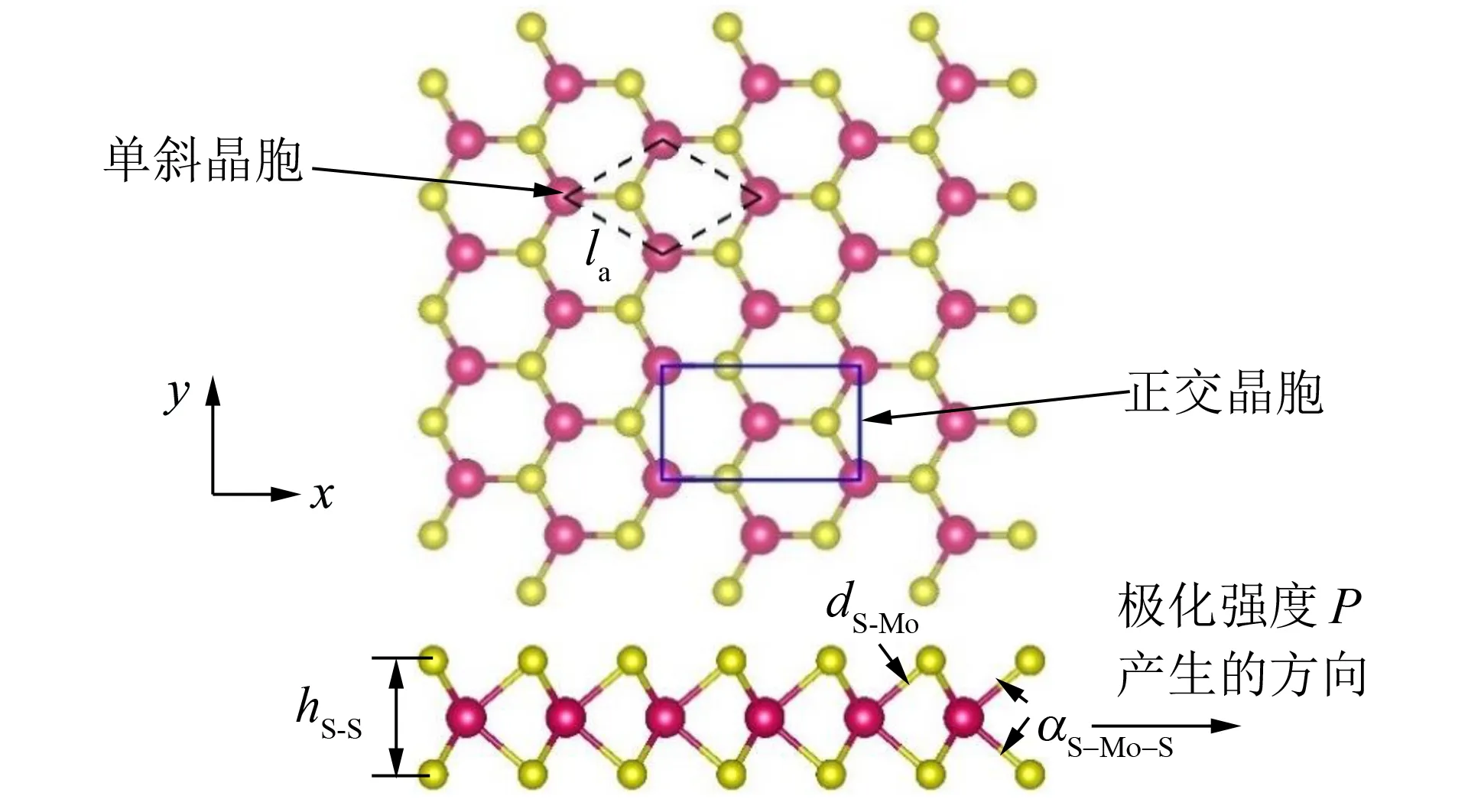
图1 单层二硫化钼(SLMoS2)结构Fig.1 Structure diagram of single layer MoS2(SLMoS2)
一般而言,不同材料体系的第一性原理计算需要选择合适的交换关联泛函[22]. 基于VASP软件包[23-24]执行单层二硫化钼基本物理性质的密度泛函计算. 仿真模拟选用周期性单斜晶胞,如图1虚线线框所示. 为实现单层二硫化钼的模拟,在平面法线方向(z向)上,设置2 nm的真空层,以避免层间相互作用. 设置体系总能量收敛阈值为1×10-6eV,原子间作用力优化参数为0.1 eV·nm-1.K点取样采用Monkhorst-Pack[25]方式,其值经过优化后选为13×13×1. 经优化后的截断能取为450 eV,体系中每个原子的总能量收敛阈值取为1×10-6eV,离子弛豫的收敛标准参数为0.1 eV·nm-1.
2 结果与讨论
2.1 晶体结构参数
三种泛函下单层二硫化钼晶格结构参数的计算结果如表1所示,同时列出了实验测试值以供对比. 数据表明,PBE和PW91的计算结果相近,而且均与实验参考值相差较小,而LDA的计算结果偏小. 主要原因是LDA没有考虑电子密度梯度对交换关联势的影响. 对于层厚度,三种泛函的计算结果相差无几,但均小于实验值. 由此,对于晶格结构参数,建议采用PBE和PW91两种交换关联泛函.

表1 三种泛函计算得到的单层二硫化钼晶格参数
2.2 能带结构和带隙
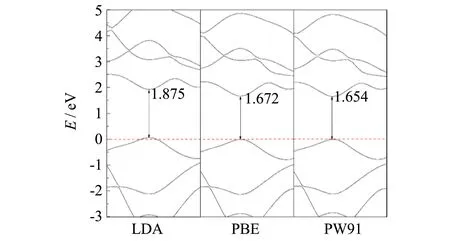
图2 三种泛函计算得到的能带结构Fig.2 Band structures calculated using three functionals
计算获得的单层二硫化钼能带结构及带隙结果如图2所示. 结果表明,所计算的单层二硫化钼为明确的直接带隙半导体,其直接带隙在1.65~1.86 eV,略低于实验测得值1.8、 1.9 eV[2, 27- 28],但与文献计算结果一致[29]. 此外,图2显示LDA泛函计算获得的带隙较接近于实测值,而GGA近似方法计算电子密度时对带隙有一定的低估[30]. 虽然不同泛函计算的带隙大小存在差异,但是其能带结构的形状却是一致的.
2.3 弹性常数
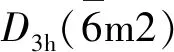
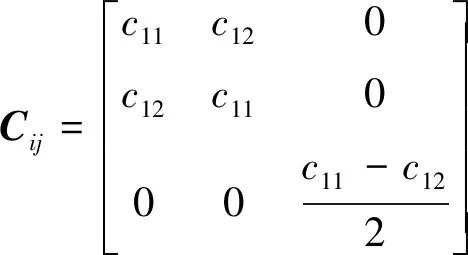
(1)
其杨氏模量(Y)和泊松比(v)可基于弹性常数c11、c12,由下式求出[15]:
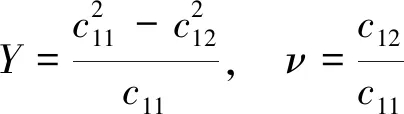
(2)
本研究计算单层二硫化钼弹性常数时,考虑了两种模式[32]: Clamped-ion(C模式)和Relaxed-ion(R模式), 如表2所示. C模式完全取自于电子所做的贡献,而R模式则全面考虑电子和离子的贡献. C模式计算结果高于R模式, 如表2所示,说明离子的松弛会软化材料刚度. 根据晶体系统的稳定性判据[15],单层二硫化钼的弹性常数满足c11-c12> 0,说明这三种泛函计算获得的体系均是稳定的. 表2还表明,LDA泛函计算获得的杨氏模量Y较PBE和PW91大,但均落入实验值范围内[33- 34],而泊松比v却相反,略低于实测值. 此外,PBE计算结果与文[14-15]一致.

表2 单层二硫化钼的弹性常数、 杨氏模量、 泊松比数值
2.4 压电常数
晶体的压电性是晶体受外力发生形变,诱发产生极性相反的束缚电荷. 只有晶体是非中心对称的,极化产生的电偶极矩才不会相互抵消,才能展现压电特性. 衡量晶体压电效应强弱的参数称为压电常数. 晶体的压电常数eijk和dijk可以由下式计算获得[12]:
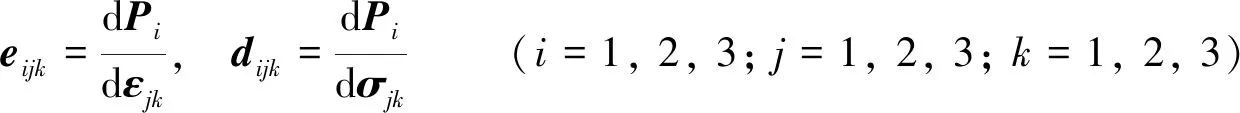
(3)
其中:σij、εij分别为应力和应变;Pi为极化强度. 根据单层二硫化钼点群特点,式(3)可简化为下式[12]:
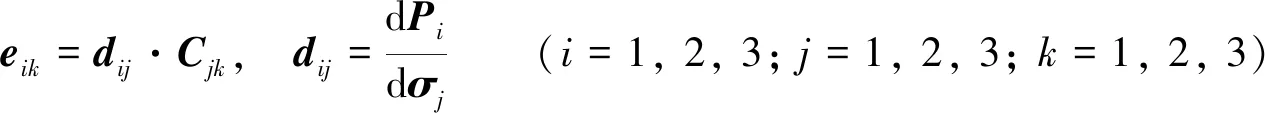
(4)
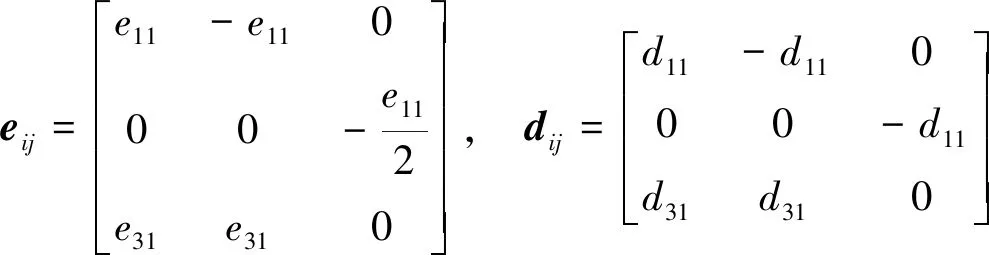
(5)
由于单层二硫化钼基面镜像对称特点,系数e31,d31可不予考虑[12],此时e11和d11的关系[12, 35]为:
e11=d11(c11-c12)
(6)
采用Berry-phase近似方法[36]计算二硫化钼沿x轴方向的应变、 应力和极化. 为便于计算压电效应,将上述单斜晶胞改为正交晶胞,如图1实线线框所示.
极化强度P是单位体积内电偶极矩的矢量和,用以反映电介质的极化程度. 对于单层二硫化钼而言,采用单位面积内的极化强度,即P=ΔPtot/A,A为晶胞面积. 根据Berry-phase近似方法,总偶极矩变化量ΔPtot包含离子和电子的偶极矩变化量之和,即: ΔPtot=ΔPion+ΔPelc分别考虑离子和电子的贡献,R和C两种应变模式下单层二硫化钼极化强度P相对应变ε11的关系曲线如图3所示. 由式(4)和式(6)可获得压电系数e11和d11,如表3所示.
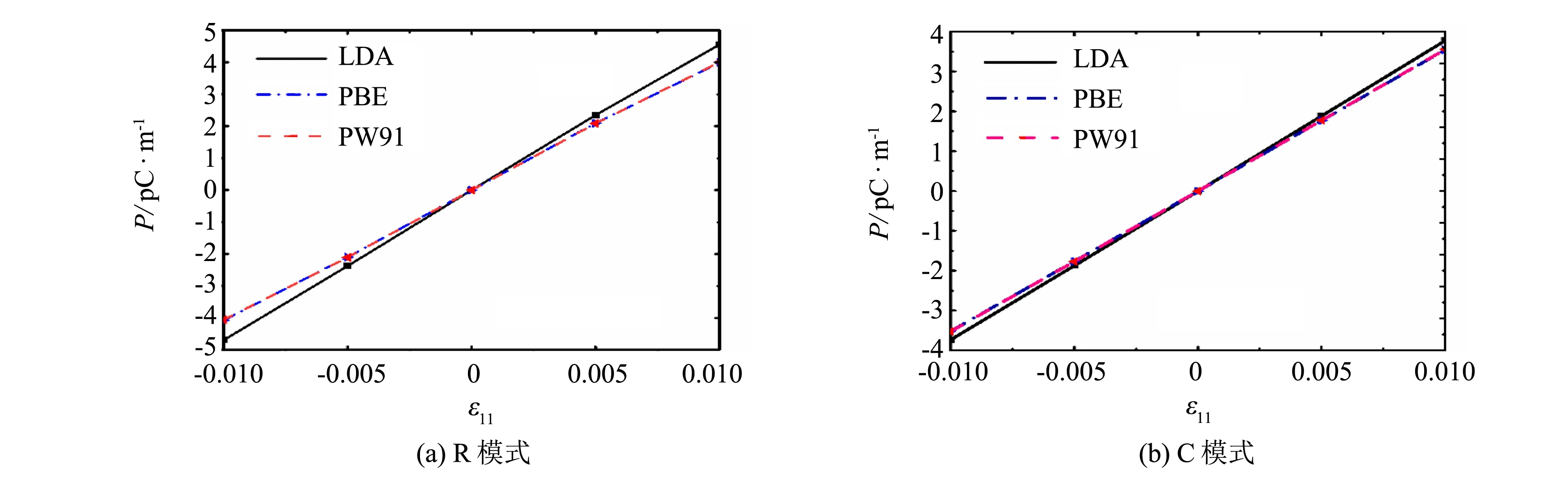
图3 极化强度与应变的关系曲线Fig.3 The curves of polarization and strain

方法R: Relaxed-ione11/nC ·m-1d11/pm∙V-1C: Clamped-ione11/nC ∙m-1d11/pm∙V-1LDA0.464.220.383.13PBE0.404.130.353.35PW910.404.180.353.40文[16](PBE)0.444.250.343.21文[17](PBE)0.373.730.312.91
由图3和表3结果知,考虑原子松弛的R应变模式获得的压电系数高于C模式,且三种交换关联泛函计算获得的压电系数e11均大于实测值(0.29±0.05)nC·m-1[10],且与文[14-15]相当. 此外,LDA泛函的计算结果较PBE和PW91偏大; PBE和PW91泛函的计算结果基本吻合. 这主要是由于PBE是在PW91基础上完善所得的. 但是,PBE具有比PW91更高的计算效率.
3 结语
采用三种交换关联泛函LDA、 PBE和PW91, 计算单层二硫化钼的晶格结构参数、 能带结构和带隙、 弹性常数和压电系数. 结果表明: LDA泛函表征的能带带隙较为符合实测数据,而PBE和PW91泛函在表征单层二硫化钼的晶格结构、 弹性常数和压电系数则较接近于实测数据; 考虑到计算效率,建议以PBE泛函计算其压电特性会更有优势. 鉴于单层二硫化钼在微电子能源领域的应用潜力巨大,后续将利用计算的参数结果进行二硫化钼压电等相关的研究工作,可为实验计算提供一定的理论依据.

