组合优化聚类与马尔科夫链的城市环卫车辆行驶工况构建方法

彭育辉，庄 源

(1. 福州大学机械工程及自动化学院，福建 福州 350108; 2. 厦门理工学院福建省客车及特种车辆研发协同创新中心，福建 厦门 361024)

0 引言

汽车行驶工况是用于汽车污染物排放、 燃油消耗等性能评估的基础数据，是影响汽车动力匹配与标定的关键因素. 截至2016年底，我国环卫车辆保有量达到34.75万辆，作为专用作业车辆，其工作范围覆盖绝大部分城市区域，工作时间长，且行驶工况特点明显区别于其它类别车辆. 美国能源部对城市垃圾转运车的运行工况进行研究，并开发了测试工况(neighborhood refuse truck cycle, NRTC)，模拟车辆在各垃圾站点间的频繁启停工况； Clark等[1-3]根据纽约市垃圾车的行驶特征开发的New York garbage truck cycle(NYGTC)也被应用于纽约市环卫车的开发测试. 但是目前绝大部分国家并没有建立针对城市环卫车的专用测试行驶工况，而是普遍采用商用车的测试工况. 中国现阶段对城市环卫车的测试工况是根据商用车的底盘属性，采用由世界重型商用车辆瞬态循环(WTVC，world transient vehicle cycle)为基础修订的C-WTVC工况进行测试[4]. 当车辆的最大设计总质量GVW大于5.5 t，用于测试油耗的特征里程分配中，市区比例10%，公路比例占30%～60%，高速占比工况30%～60%，显然，这与城市环卫车的实际运行状况差距较大.

国内外研究学者对专用汽车行驶工况的构建方法做了大量研究. 文[5]利用多参数统计理论构建自卸车循环工况； 文[6]以聚类分析方法构建重型载货汽车行驶工况； 文[7-8]利用大样本数据，通过短行程的划分，采用“最佳增量法”分别构建了重型客车与城市公交车的行驶工况. 文[9]最早提出马尔科夫法并应用于美国加利福尼亚州的LA01工况构建上，文[9-11]进一步将车辆行进过程抽象为离散随机的马尔科夫过程，基于状态转移概率合成车辆行驶工况. 相对而言，目前国内对于环卫车行驶工况的研究涉及极少，文[12]是以一辆环卫车行驶数据为研究对象，采用两阶段聚类法构建了西安市环卫车行驶工况，但是其采集区域与路线固定，试验车辆单一，采集时段覆盖较少，使得构建结果的代表性不够理想.

为研究城市环卫车辆的实际工况特征和合理的工况构建方法，以福州市内3辆清洁环卫车持续一周各时段的实际道路行驶数据为研究对象，提出一种适用于城市环卫车辆的工况构建方法. 通过均值化处理改进传统主成分分析 (principal component analysis，PCA)，提高各主成分提取到的车辆行驶信息，对特征参数降维后构造得到的各主成分进行k均值聚类，将原始数据样本划分为两类，有效区分环卫车在清洁作业时(以稳定中低车速行驶，加减速平缓)和作业结束返程时存在的两种明显不同的行驶特征； 再将每一类行驶过程视为一个随时间变化的马尔科夫过程，基于马尔科夫模型构建其代表工况，充分体现其瞬时工况的随机性. 所构建的福州市环卫车代表工况相较于国家现行标准工况能更好地反映福州市环卫车实际运行状况，更适用于福州市环卫车辆的开发测试.

1 数据采集与分析

1.1 实测数据采集

将车载数据采集终端接入车辆OBD接口，以1 Hz的频率实时采集测试车辆在行驶过程中的速度、 GPS位置、 瞬时油耗等参数，并与数据监控平台进行通讯，传输采集数据. 选取3辆福州市清洁环卫车辆，采用自主驾驶法，按照其正常工作路线行驶采集数据，而非规划的固定试验路线，保证采集的数据能真实有效地反映福州市环卫车的实际运行工况特点. 车辆行驶区域覆盖福州市各主要干线道路，数据采集周期为连续一周，含工作日和周末非工作日的各个时段. 采集到总计约180 ks有效的车辆实际道路行驶数据.

1.2 实测数据预处理及分析

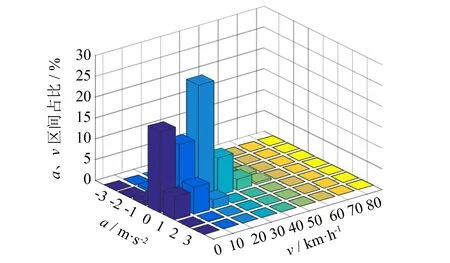
图1 实测数据速度-加速度频率分布图Fig.1 Frequency of speed-acceleration distribution

车辆行驶数据在采集过程中，由于采集设备故障、 环境条件等客观因素导致采集到的数据存在异常值，需对原始采集数据做滤波处理，消除影响. 在实际行驶过程中，受环卫车辆动力与制动性能、 道路交通条件和环卫作业规定等限制，对加速度超过-4～4 m·s-2阈值区间、 存在缺失值、 加速或减速时间比例为0的环卫车辆行驶数据，可判定为是由于GPS振动漂移或信号屏蔽等原因导致的数据异常，此类数据片段做剔除处理； 剔除异常值后车辆实测数据的速度-加速度频率分布情况如图1所示，行驶数据主要分布在0～40 km·h-1车速，-1～1 m·s-2加速度的区间内，具有车速较低，加减速平缓等专用作业车辆的行驶特点.

2 环卫车代表工况构建

2.1 运动学片段划分

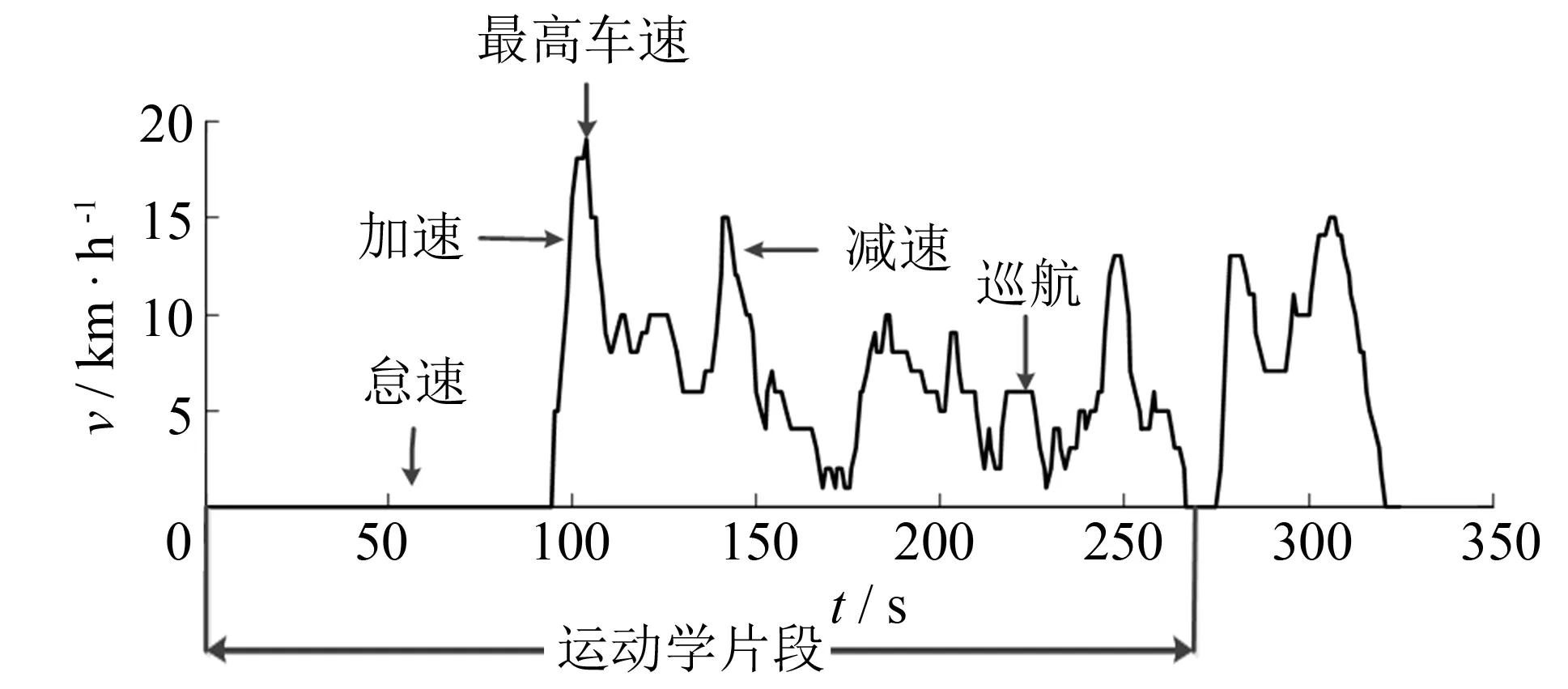
图2 运动学片段Fig.2 Micro-trips

车辆行进过程中，因路况和交通因素，存在多次怠速、 加速、 减速与匀速的状态. 如图2所示，运动学片段为某一怠速开始至下一怠速开始前的区间[13]. 汽车行进过程可视为大量运动学片段的衔接，按这一原则对原始工况数据进行划分，共得到2 070个运动学片段. 为最大限度反映每个运动学片段的行驶特征，选取如表1所示的15个特征参数来描述运动学片段，并计算出每一片段的特征参数值，构造为特征参数矩阵.

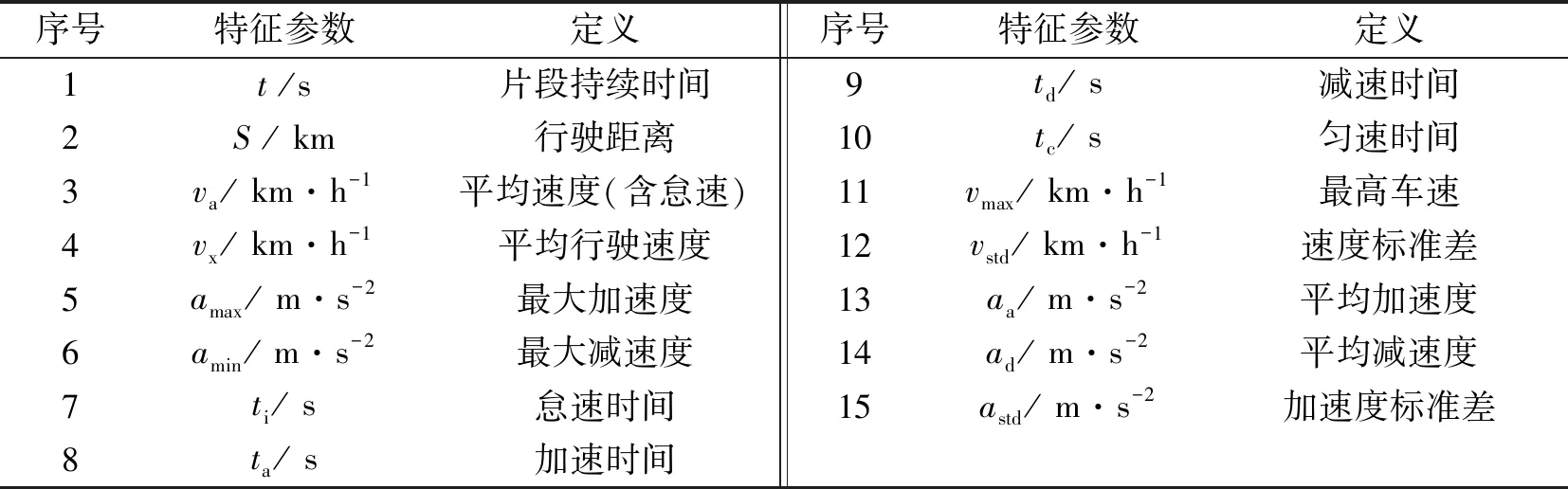
表1 用于描述运动学片段的15个特征参数

2.2 基于主成分分析法的特征参数降维

各特征参数因量纲不同将导致各自取值较为离散，使得大方差变量在后续分析时会优先照顾，降低计算准确性，因此特征参数降维前需先做标准化处理，消除量纲不同造成的影响[14]. 构造包含15个特征参数的矩阵A为:

(1)

式中：aij(i=1, 2, …,m；j=1, 2, …,n)是第i个运动学片段的第j个参数.

在主成分分析前先求出矩阵A的协方差矩阵A′，对A′做均值化处理，避免各参数变异程度信息丢失. 令：

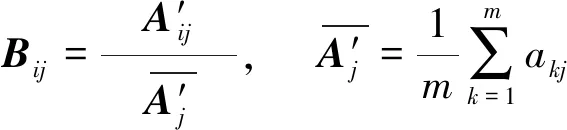
(2)

即用协方差矩阵A′中的每一元素aij除以所在列的所有元素均值，得到均值化后的特征参数矩阵Bm×n. 统计学上已证明[15]，经过均值化处理后的矩阵B将不改变各参数变量的相关系数，且能全面地包含原始数据信息.

对均值化处理后的特征参数矩阵做主成分分析，利用线性变换构造出新变量(即主成分)，使得各主成分间两两独立且线性无关，消除了所选取的各特征参数在描述运动学片段时存在的信息重叠，同时保留了原变量的绝大部分特征信息. 研究表明，若主成分的特征值大于1，且累积贡献率在80%以上，即满足行驶工况开发要求[16]. 特征参数矩阵在主成分分析后得到的各主成分相应特征值、 贡献率及累计贡献率如表2所示，可以看到，前三个主成分的特征值均大于1，累积贡献率为85.332%. 因此选取前三个主成分来表征15个特征参数所包含的行驶信息，能达到降维目的.

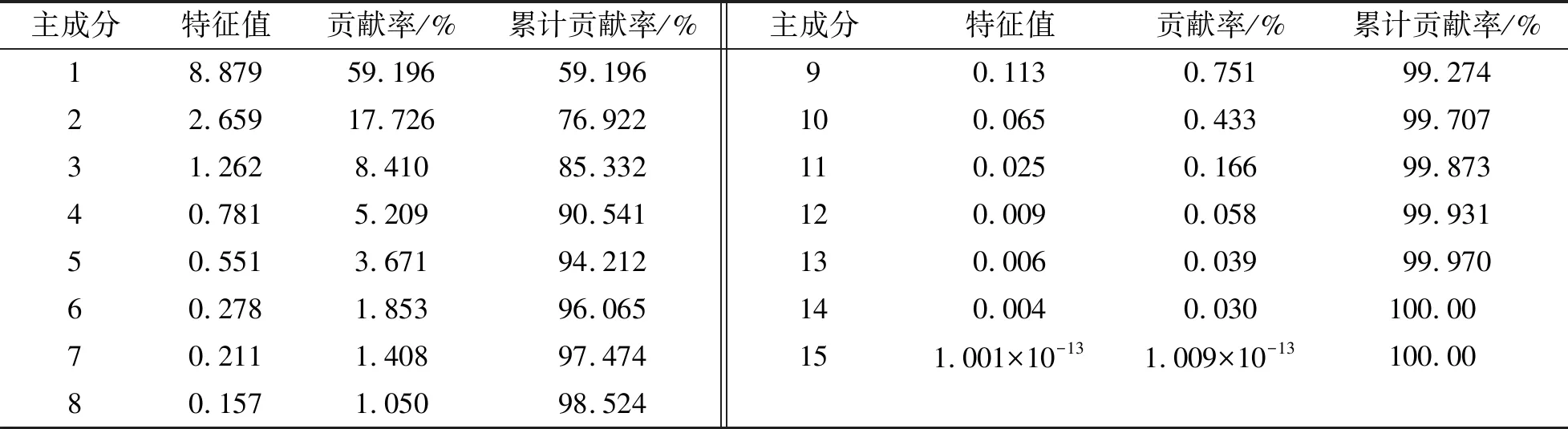
表2 主成分贡献率及累积贡献率

2.3 k均值聚类分析

聚类的过程就是把样本集分类成不同组别的过程.k均值聚类是非监督快速聚类，能够使样本分类后达到类内相似度高，类间相似度低的目的[17]. 具体过程为：

1) 针对样本数据特点确定k个初始聚类中心.

2)计算每一样本xi中的第k个变量值到最近聚类中心zj的欧式距离，确定样本类别； 欧式距离能很好表征类别间不相似性. 欧式距离的计算公式如下：

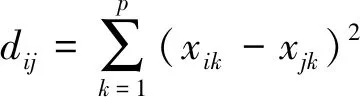
(3)

3) 重新计算求出每一聚类的均值，将这一均值作为新聚类中心.

4) 迭代步骤2)～3)，直至聚类中心收敛为定值.

按上述步骤，对主成分进行k均值聚类，把行驶特征相似的运动学片段聚为同一类，获得了两类片段样本集，两类片段样本各特征参数值的对比如表3所示. 可以看到，两类片段样本集的特征参数差异明显，分别代表两类不同的行驶特征. 聚类1、 聚类2的样本时间长度比例分别为69.60%和30.40%，其中聚类1的平均车速较低，仅为16.45 km·h-1，同时匀速比例Pc达到40.3%，加速比例Pa、 怠速比例Pi比例和平均加速度都不高，表明聚类1样本为环卫车在进行清洁作业时，缓慢稳定行驶的片段样本集； 聚类2的加速状态比例达到37.3%，平均车速也较高，而匀速时间比例仅为18.3%，表明聚类2样本为环卫车完成清洁作业后，跟随城市车流驶回停车场的片段样本集.

表3 每一聚类的特征参数

2.4 基于马尔科夫链法合成代表工况

环卫车在行进过程中，车速是随城市车流根据交通情况随机变化的，因此将其行驶过程视为一个随时间变化的离散马尔科夫过程，能够充分体现其瞬时工况的随机性.

2.4.1状态划分

由于行车过程是在加速、 减速、 匀速、 怠速工况间不断轮换，基于马尔科夫模型进行汽车行驶工况构建时，采用这四种确定的工况对实测数据的速度-时间序列进行划分，每个被划分出的片段定义为模型事件，记为Zτ={Z1,Z2, …,Zτ| (τ=1, 2, …,T)}，再将运动学特征接近的片段整合为模型事件集，形成马尔科夫模型中的“状态”[18]，记为S={S1，S2，…，Sτ| (τ=1, 2, …,k)}. 状态划分后，在所构建马尔科夫模型中，即能以状态(隐性信息)表征车速(显性信息)，因此状态划分是工况构建的首要.

2.4.2状态转移矩阵的计算

对于所有的模型状态S1,S2, …,Sτ，状态Sτ的概率仅和前一状态Sτ-1相关联，离散的马尔科夫链在固定时域下具有稳定性和齐次性，未来时刻的取值只与当前时刻取值有关，而与过去时刻取值无关[19].

对于从任意τ-1时刻到τ时刻，其条件概率有：

P={Zτ=s|Zτ-1=r}=P{Zτ+τ′=s|Zτ+τ′-1=r}(τ′=-(τ-1),-(τ-2), …, -1, 0, 1, …)

(4)

利用最大似然估计法计算各个状态间的转移概率Prs，全部转移概率构造为转移概率矩阵.

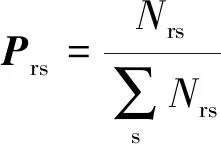
(5)

其中：Nrs指时间从τ-1到τ，状态从r转移至s的事件数.

基于马尔科夫模型计算时，采用随机选择连续片段的传统方法不能确保每个模型事件在工况中的最佳代表性. 因此本文利用最大似然估计法，以估计状态转移概率的方法取代传统的随机片段法，在车速隐马尔科夫链中，通过转移概率来不断预测下一状态，保证选取模型事件的代表性，各状态间转移概率矩阵计算结果见表4.

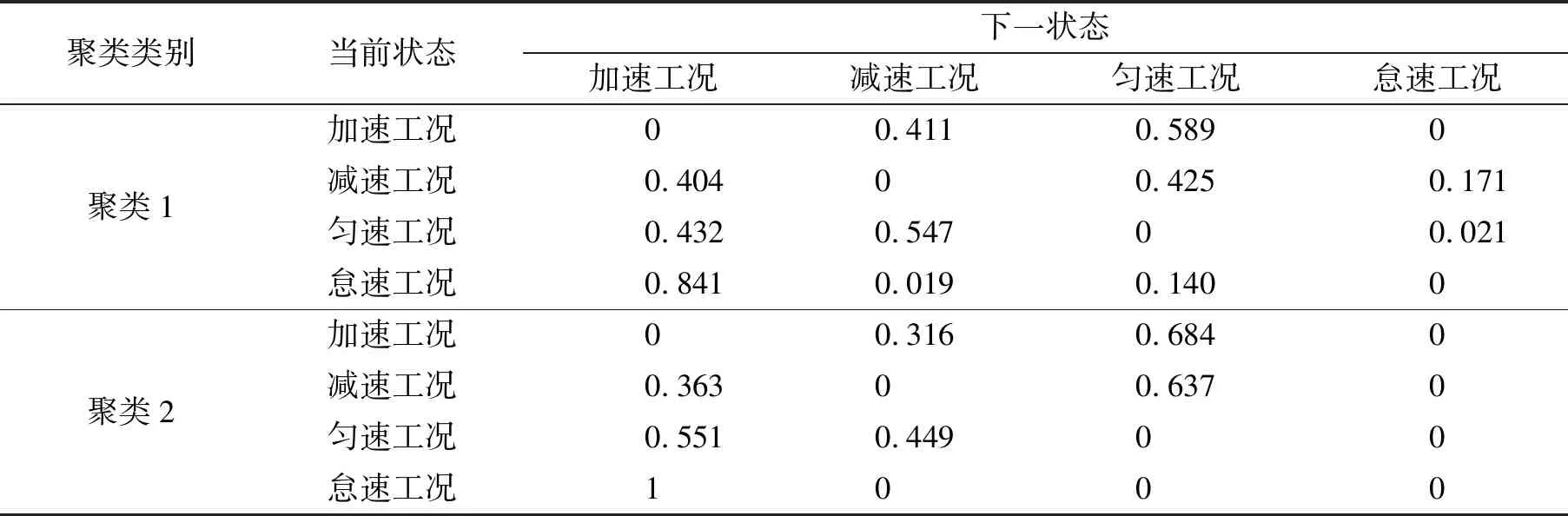
表4 各状态间转移概率矩阵

2.4.3环卫车代表工况合成

按照上文提及的马尔科夫法基础理论，以下述原则合成候选工况.

1) 根据聚类1、 聚类2占原始工况数据的时间比例，计算出环卫车在两类工作模式下的候选工况长度；

2) 为便于行驶工况在台架测试中的应用，以怠速工况状态作为初始状态，而后的每一个行驶状态是根据转移概率矩阵和当前时刻行驶状态确定；

3) 状态转移矩阵各个状态间的转移概率≥0；

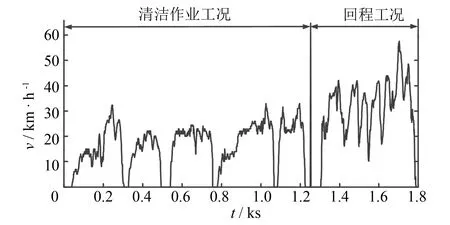
图3 清洁环卫车代表行驶工况 Fig.3 Representative driving cycle of cleaning trucks

4) 由最大似然估计法不断进行下一状态筛选，直至合成候选工况达到预定长度.

将合成的聚类1、 聚类2候选工况与实测数据每一个状态的行转移概率做K-S双尾检验，筛选出相似性水平不小于0.9的候选工况，以确保二者的状态转移矩阵来自同一样本分布. 将两类候选工况随机排列组合，筛选出特征参数平均误差最小的合成工况作为最终代表工况. 最终代表工况中两类工况的时间占比与两种聚类样本在实测数据中的时间占比相同. 按时间比例合成的福州市清洁环卫车代表工况如图3所示.

3 行驶工况有效性检验

3.1 基于运动学参数的有效性检验

为验证代表工况的准确性，将所构建的福州市环卫车代表工况的主要特征参数与实际试验采集数据的主要特征参数进行对比，其相对误差结果如表5所示. 代表工况与实际试验数据相比，各特征参数的相对误差均在7%以下，相对误差绝对值的算术平均值为4.46%. 同时，代表工况中的片段运动学特征和车辆实际行驶状况基本一致，符合环卫车在实际行进过程中的行驶特点.

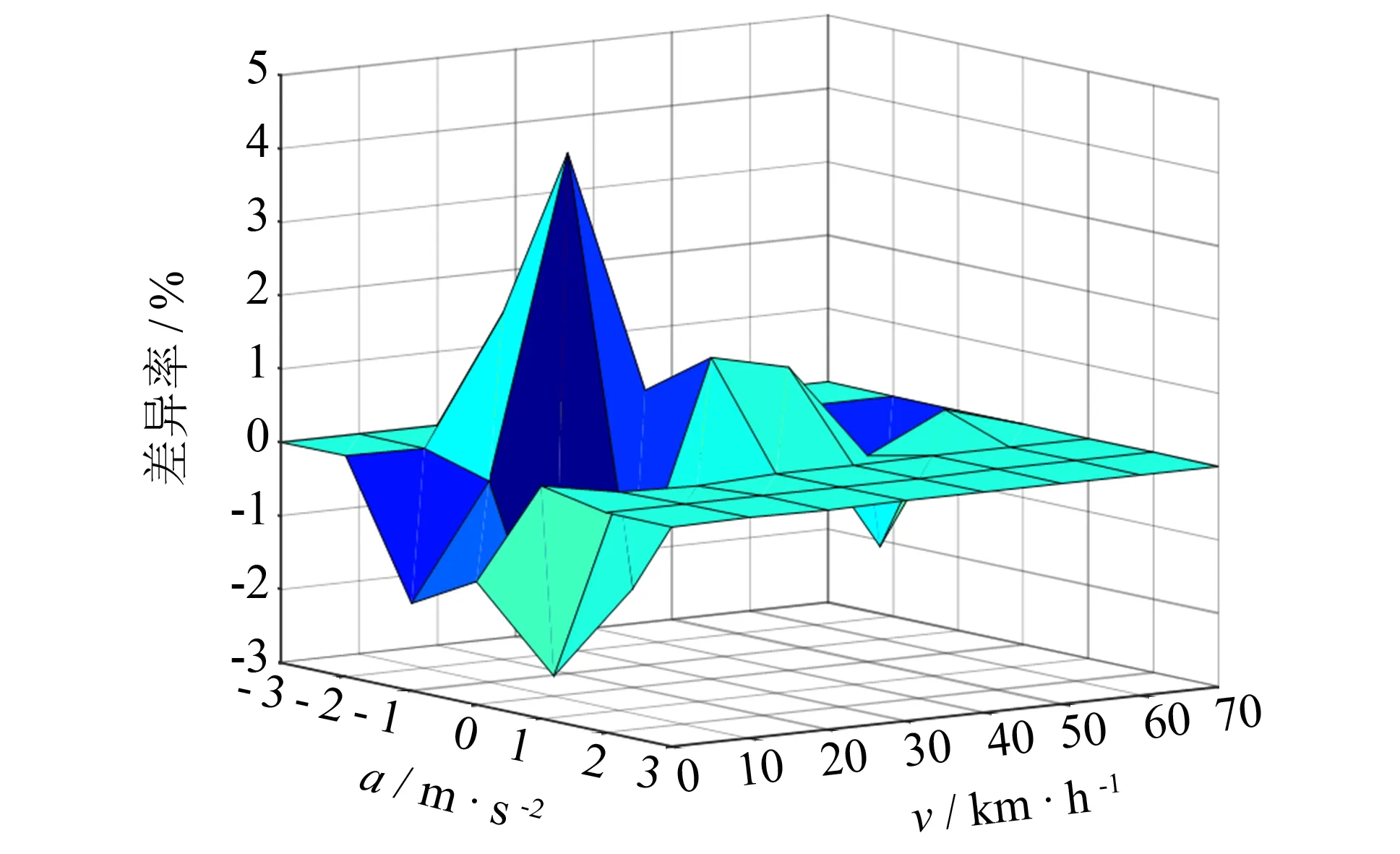
图4 试验数据与代表工况速度-加速度联合分布差异率 Fig.4 SAFD difference between the sampling data and the representative driving cycle

其次，从速度和加速度两个角度验证代表工况和试验数据之间的差异率，采用速度-加速度联合分布图(speed-acceleration frequency distribution, SAFD)来验证代表工况的准确性, 如图4所示. 从图4可见，试验数据与代表工况数据在速度加速度各个分布区间上的差异率都维持在±5%以内，说明所构建代表工况能很好地反映试验数据样本，表征车辆的实际行驶特征.

3.2 工况对比分析

将构建的福州市清洁环卫车代表工况(Fuzhou sanitation truck cycle, FZSTC)与现阶段我国对城市环卫车进行测试的C-WTVC标准工况进行对比，如表6所示，其中FZSTC-1为清洁作业工况，FZSTC-2为回程工况. 可以看到，环卫车在清洁作业时，匀速时间比例Pc较大，达到39.19%，而在回程时加减速较频繁，加速时间比例Pa能达到40.29%. FZSTC与C-WTVC在平均车速va和最高车速vmax上差异明显，主要原因是环卫车在清洁作业时的特殊性要求，必须保持稳定的较低车速，同时为了专用车辆的行车安全，即使在回程时，环卫部门也规定环卫车不能以较高的车速行驶，因此FZSTC整个循环不存在高速段，最高车速仅有58.12 km·h-1. 考虑到实际行驶工况特征，将C-WTVC测试循环去除432 s高速段后的工况命名为C-WTVC*，考察其与FZSTC的差异. 结果表明，C-WTVC和C-WTVC*都与FZSTC差异较大，尤其在匀速时间比例Pc和平均车速va差异明显. 这说明，现行对环卫车测试采用的商用车标准测试循环C-WTVC并不能有效反映出城市环卫车辆的实际运行状况，不适用于城市环卫车辆的工况测试.

表6 所构建代表工况与标准工况的比较

4 结语

提出一种改进PCA降维和k均值聚类的组合优化方法，提高各主成分所提取到的车辆行驶特征信息量，同时对环卫车不同行驶特征做有效分类； 以估计状态转移概率法取代传统的随机片段法，应用马尔科夫法按时间比例合成福州市环卫清洁车的代表工况.

1) 所提方法构建的代表工况与实际采集的行驶数据相比，各特征参数的相对误差均在7%以下，且SAFD差异率都维持在5%以内. 说明基于所提方法开发的代表工况能很好地反映试验数据样本，表征福州市环卫清洁车辆的实际行驶特征，证明了所提工况构建方法的有效性和合理性.

2) 现行对环卫车测试采用的商用车标准测试循环C-WTVC与福州市环卫车辆的实际行驶状况有较大差异，并不能有效反映出城市环卫车辆的实际运行状况，不适用于城市环卫车辆的工况测试. 根据所提方法而所构建的环卫车代表工况能更真实表征城市环卫车辆的行驶工况，为我国环卫车辆行驶工况的开发提供一种有效的借鉴.