定点投影问题的研究

张红，康彤

(中国传媒大学理工学部，北京 100024)

1 引言

随着大数据时代的到来，数据分析在社会各领域的应用也越来越广泛，而其中视频数据分析也发挥着巨大的作用。

2

2.1 符号说明及名词定义

符号说明及名词定义如表1所示。

2.2 模型建立与求解

2.2.1 建模准备

由问题的分析可知：建立出影子长度随时间变化的模型，再将题目中给出的北京的数据带入计算得出影子长度关于时间的变化曲线。

2.2.2 模型的建立过程

分析得到太阳高度角。如图1所示，H就是太阳高度角。

在图中该地有一根长为M木杆，它的影子长度、杆长以及太阳高度角的关系如图2所示。

表1

图1

图2

我们由图得到影长关于太阳高度角的表达式：

(1)

我们得出太阳高度角的三角公式：

sinH=sinαsinβ+cosαcosβcost

(2)

太阳赤纬的正弦值的表达式为：

sinβ=0.39795cos[0.98563(N-173)]

(3)

太阳时角所遵循的关系为

ω=15°×(ST-12)

(4)

其中ST=T±t0，T为某地时间(注：当某地所在的经度时<120°时，ST=T-t0当某地所在的经度>120°时，ST=T+t0。其中t0=(120°-φ)/15°，φ为当地经度)。

我们将公式(1)-(4)联立就可以建立影子长度关于太阳高度角的数学模型。

首先得到的是太阳高度角正弦值的变化，如图3所示。

图3

在图3中，我们可以看出，太阳高度角的正弦值在9：00-15：00是呈抛物线状的，并且其变化趋势是先增大后减小，在大约12：30的时候达到最大。在此基础上，由我们建立的模型，根据2015年10月22日得到太阳赤纬β，进而求出β的正弦值sinβ和余弦值cosβ。由东经116度23分29秒可以得出太阳时角关于北京时间T的表达式，再由太阳高度角的三角公式得出太阳高度角关于时间T的表达式。最终得到太阳影长的变化曲线，如图4。

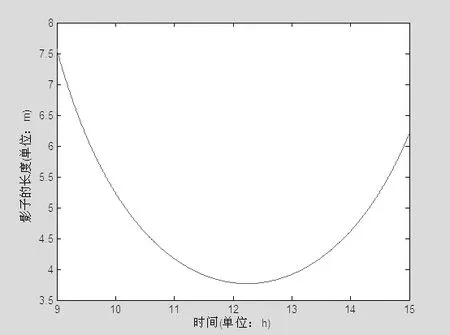
图4

在图4中，影长由9：00-15：00的变化是呈抛物线状的，并且是影子长度先减小后增加，在大约 12：30的时候影子长度达到最小。

3 总结

本文通过大量阅读文献，建立了一系列科学的假设，忽略对结果影响较小的因素，在大大简化了模型与算法的情况下得到了较好的建模效果。针对问题我们分析太阳高度角与影长的关系，并根据两者的关系建立模型，首先得到的太阳高度角的正弦值的变化曲线图像，为以后方便大家研究影长的曲线变化做了铺垫。