基于GA和DE的非均匀等离子体介质参数重构算法研究

冯雪健，邓浩川，韦笑，殷红成

(1.中国传媒大学信息与通信工程学院，北京 100024；2.电磁散射重点实验室，北京 100854)

1 引言

电磁波的散射反演是电磁计算领域一个重要方向，在过去的几十年里，被广泛应用于医学诊断、无损检测和地下探测等领域。散射反演通常是指通过目标电磁波的散射场来重构目标内部介质的参数分布，但是由于散射反演问题有很严重的非线性和病态性，所以如何快速有效地重构目标内部介质参数分布是目前散射反演领域的研究热点。具有色散特性的冷等离子广泛分布于地球电离层[1]，其参数的有效重构对于军事目标成像和通信等都有很大的现实意义。

近年来，国内外学者对色散介质的散射反演问题进行了广泛的研究，并在多种算法上取得了显著的成果。Sailing He等基于FDTD算法和共轭梯度法反演了一维分层色散有耗介质的电参数分布[2]，并与实验室测量结果进行了对比验证。在2011年，文献[3，4]中用类似的方法给出了一维洛仑兹模型和二维德拜模型的介质参数反演算法。以上方法均是通过严格的数学方法求重构参数梯度并与梯度类优化算法相结合来重构目标参数分布的，具有较高的计算精度，但容易陷入局部最优解且计算过程复杂。作为蒙特卡罗方法的一种，遗传算法(Genetic Algorithm -GA)在文献[5]中被用于参数重构。在2005年，文献[6]将粒子群优化(Particle Swarm Optimizer-PSO)算法应用于微波成像。随后，A.Semnani等提出了傅里叶级数展开和差分进化(Differential Evolution-DE)算法相结合的介质参数重构方法，并且与立方B曲线展开方法进行了对比[7]。2017年，Z.Q.Zhang等人用频域双共轭梯度快速傅里叶变换(bi-conjugate gradient fast Fourier transform-BCG-FFT)算法作为前向正演算法和 变分波恩迭代(variational Born iterative method-VBIM)算法作为后向重构算法，重构了非磁冷等离子体目标的参数分布[8]。对于非均匀的等离子体介质，本文采用时域电流密度卷积FDTD 方法为正演算法并分别与GA和DE算法[9]相结合构成等离子体介质参数反演算法。仿真实验中采用宽频带的高斯脉冲源作为激励源，相比域频域方法能够有效减少算法整体复杂度。仿真结果表明，当反演区域为均匀等离子体介质和非均匀两层等离子体介质时两种反演算法都能有效的重构等离子体介质参数，并且DE算法有比GA算法更好的重构精度。当反演区域为有严重病态性的多层非均匀等离子体介质时，两种反演算法的参数反演结果都变得不够准确。最后引入立方B样条曲线展开法对等离子介质参数进行展开，仿真实验表明改进算法能够使反演算法快速收敛并且能有效改善参数反演的准确度。

2 理论推导

在各向异性色散碰撞磁化等离子体介质中，Maxwell方程组和相关的本构方程可以写为：

(1)

(2)

(3)

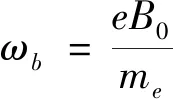
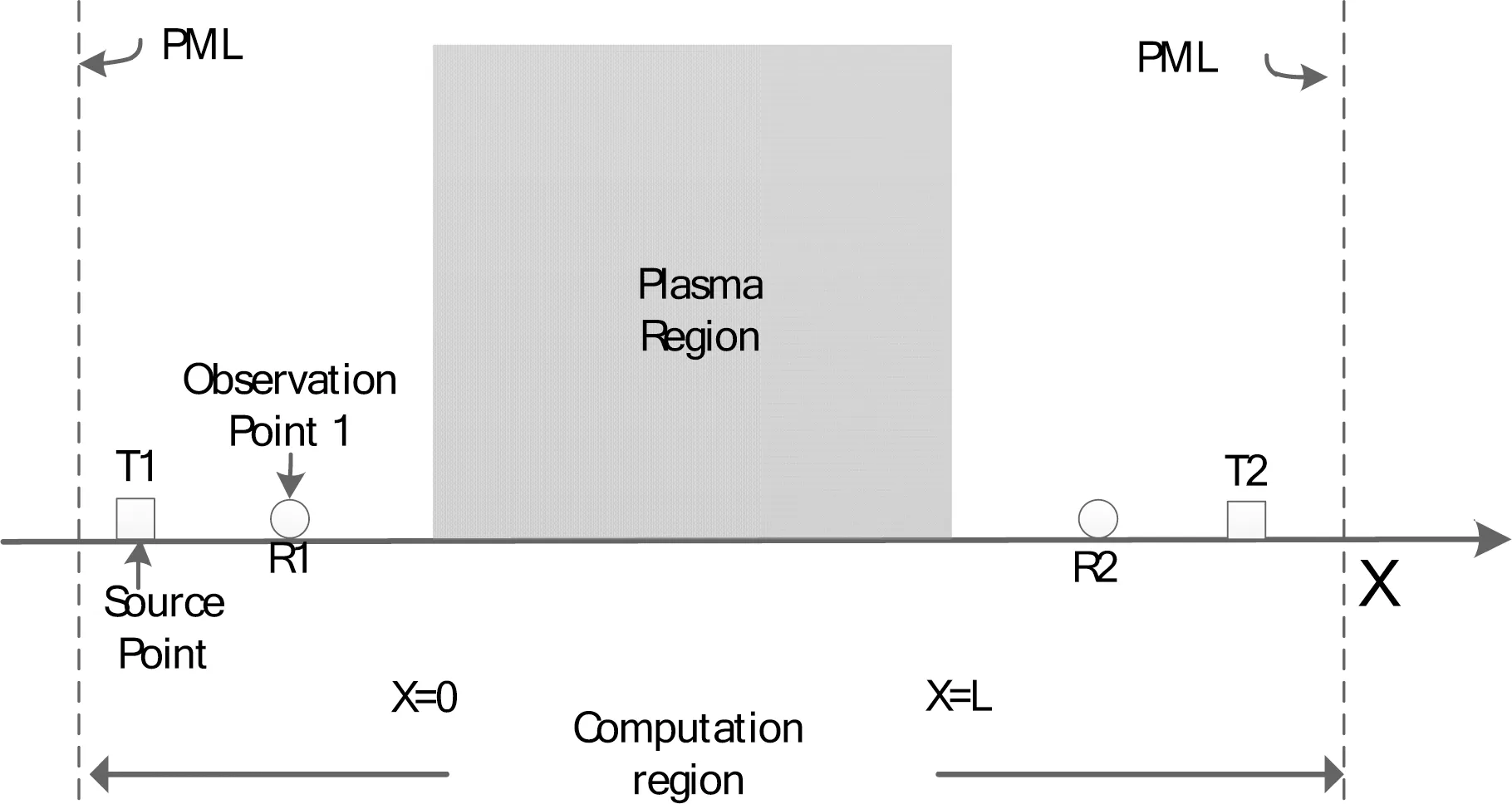
图1 一维等离子体介质参数重构计算模型

(4)

其中i，k分别表示仿真实验的入射点和接收点，T为观察点处的总采样时间，η0为自由空间波阻抗。

用GA算法作为优化算法时，考虑到对多层非均匀等离子体参数进行反演时有较多的反演参数，如果采用二进制编码则会导致编码长度过长从而造成编程实现困难。因此，本文将对反演参数进行实数编码，于是需要对GA算法的选择、变异和交叉操作进行适当修改。

(1)选择操作。由于反演问题要求的是代价函数Fcost的最小值问题，于是在采用轮盘法进行选择操作时需要在求个体选择概率时做如下修改：

1.对个体代价函数值进行反转得到个体适应度值：

fitvalue(i)=1/Fcost(i)

(5)

2.计算得到所有个体适应度值的总值：

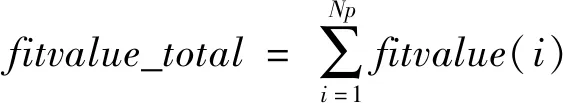
(6)

3.计算得到个体的选择概率值：

selection_value(i)=fitvalue(i)/fitvalue_total

(7)

其中i=1，2，3...Np表示种群中的个体。经过上述三步操作可以确保越小的Fcost拥有越大的被选择概率。

(2)变异操作。本文中实数编码的变异形式为：

pop(i，：)=pop(i，：)+λm·rand·pop(i，：)

(8)

其中pop(i，：)表示第i个种群个体的参数向量，λm为变异系数，rand为(-1，1)之间的随机数。

(3)交叉操作。本文中对于随机选择的两个实数编码个体(i，j)参数向量的交叉操作为：

pop(i，：)=pop(i，：)+λc·(pop(i，：)-pop(j，：))

(9)

pop(j，：)=pop(j，：)+λc·(pop(j，：)-pop(i，：))

(10)

其中λc为交叉系数。

在用DE进化算法作为优化算法时，与GA算法区别主要体现在变异和交叉这两个操作上。本文中，变异和交叉的形式分别如下：

(1)变异操作。差分进化算法中实现变异的方法是：在种群中随机选取两个不同个体，将它们的参数向量进行差值运算并乘以变异概率用以生成新的个体。

temp_popn+1(i，：)=popn(rand_1，：)+λm·(popn(rand_2，：)-popn(rand_3，：))

(11)

其中n表示进化的代数，λm为变异概率，rand_n，n=1，2，3表示随机选取的[1，Np]之间的数，Np为种群数目。

(2)交叉操作。差分进化算法中实现交叉操作的方法是：对第n代种群个体(popn(i，：))和经过变异操作后的临时种群(temp_popn+1(i，：))个体进行交叉操作来生成第n+1代种群个体。

(12)

其中，j表示种群个体参数向量中的第j个参数分量，RC表示交叉概率，j_rand为随机选取的必交叉分量用来保证每个个体最少有一个分量进行了交叉操作。

GA、DE算法用于等离子体介质参数的反演算法流程如图2所示。

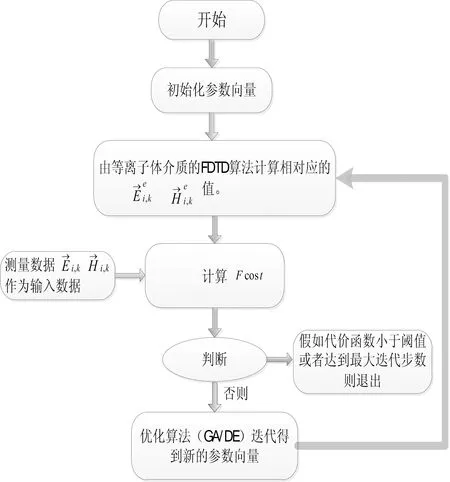
图2 反演算法流程图

3 散射参数的表示方法

本文分别用了两种参数重构方法：一种是直接表示法，一种是立方B样条曲线展开法。其中，对均匀等离子体和两层非均匀等离子体介质目标参数重构情形采用了直接表示法，对于多层非均匀等离子体介质目标参数重构情形采用了直接表示和立方B样条曲线展开两种方法表示。

(1)直接表示法。假设等离子体介质目标区域离散为N个离散网格，每个网格的介质参数相互独立，那么一维反演问题用直接表示法可以写成如下形式：

(13)

(14)

(15)

其中

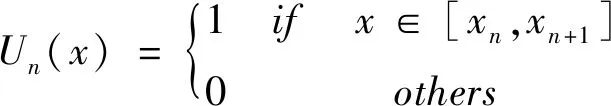
(16)

(2)立方B样条曲线展开。运用曲线拟合的思想，将需要反演的非均匀等离子体区域介质参数值看作是曲线上的一些离散点，然后用一段曲线近似拟合。立方B样条曲线拟合作为近年来广泛用于工程应用的曲线拟合方法，拥有良好的局部拟合效果。在立方B样条拟合中，通过一系列称为节点的实数将整个拟合区域划分为很多空间间隔。空间间隔长度也就是两个相邻节点之间的距离，用Δl表示。节点的分布形式有均匀分布和非均匀分布两种，由于我们通常没有任何关于反演问题中重构区域的参数曲线形状的先验信息，于是本文中将采用节点均匀分布的形式。由于立方B样条的基函数是三阶的，于是每个基函数需要五个节点也即四个空间间隔来确定。因此，拟合曲线上每一个点的值都需要四个包含这个点的基函数来组合确定。立方B样条曲线的基函数形式为：

(17)

(18)

(19)

(20)

其中t∈ [0，1]为所求点到所在间隔区间起始节点的距离与间隔区间长度Δl的比值。假如对于一维反演问题有Nc个控制点，那么整个反演区域被划分为Nc+3个间隔。那么有：

(21)

则拟合区间中某一点x对应的t值为：

(22)

其中Ni表示点所在的间隔区间，“integer”表示往零方向取整数。

于是，等离子体介质参数在立方B样条曲线中可以表示为：

(23)

(24)

(25)

其中1≤Nc-i≤Nc。

4 仿真实验

如图1所示，等离子体重构区域长度为L=22.5cm，正演算法采用电流密度卷积FDTD。激励源为调制高斯脉冲，表达式为

(26)

其中w=2πf，f=5e8Hz，τ=60dt，t0=0.8τ。离散网格大小设为Δx=0.75cm，则等离子体区域被离散为30个网格。c为自由空间的光速，离散时间步长为Δt=Δx/c/2。GA和DE算法的种群数都设为50个、，最大迭代步数设为200，电流密度卷积FDTD正演计算时间步数为1000步。遗传算法的交叉和变异概率都为0.5，差分进化算法的变异和交叉概率为λm=RC=0.5。

实验一，目标等离子体区域为均匀等离子体介质情形。已知目标等离子体区域为均匀等离子体介质，则式(13)-(15)中的系数an、bn、cn在不同离散网格的值都是相同的，也即是在重构均匀等离子区域介质参数时只有3个未知量。表1为等离子体介质参数反演的绝对误差和相对误差，其中yT表示理论值，yR表示反演值，可以看出以GA算法和DE算法为优化算法来重构均匀等离子体介质参数都有很好重构准确度，并且DE算法有比GA算法更好的重构准确度。图3为GA算法和DE算法重构等离子体介质参数时代价函数值随进化代数的变化曲线，也可以看出DE算法有更好的重构准确度。

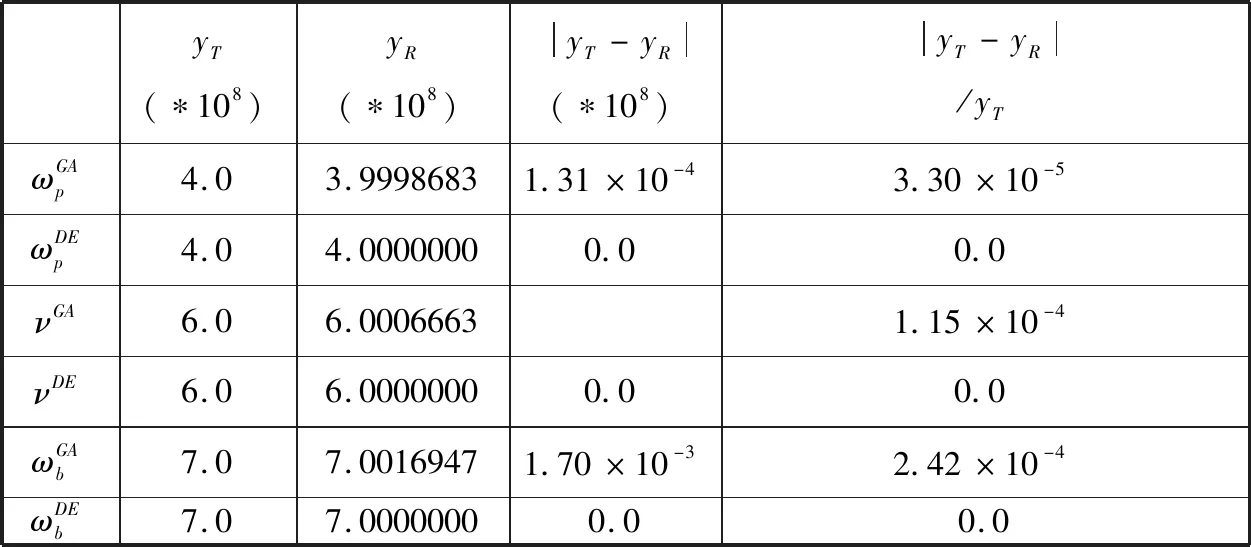
表1 实验一中的等离子体介质参数反演的绝对误差和相对误差

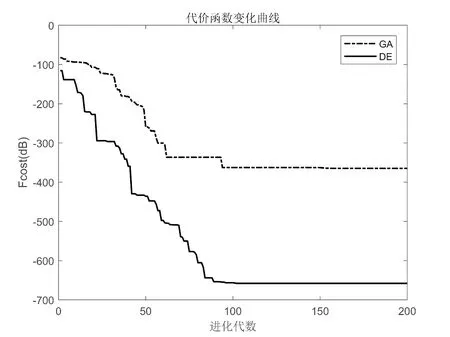
图3 实验一中 GA算法和DE算法重构等离子体介质参数时代价函数值随进化代数的变化曲线

实验二，目标等离子体区域为两层非均匀等离子体。在这个实验中，已知等离子体区域为等长的两层均匀等离子体介质，长度为L1=L2=L/2。则式(13)-(15)中的系数an、bn、cn在L1、L2内的离散网格的值是不相同的两种情形，也即是在重构均匀等离子区域介质参数时有6个未知量。从表2为等离子体介质参数反演的绝对误差和相对误差，可以看出以GA算法和DE算法为优化算法来重构两层非均匀等离子体介质参数都有很好重构准确度，并且DE算法有比GA算法更好的重构准确度。图4为GA算法和DE算法重构等离子体介质参数时代价函数值随进化代数的变化曲线，也可以看出DE算法收敛更快并有更好的重构准确度。

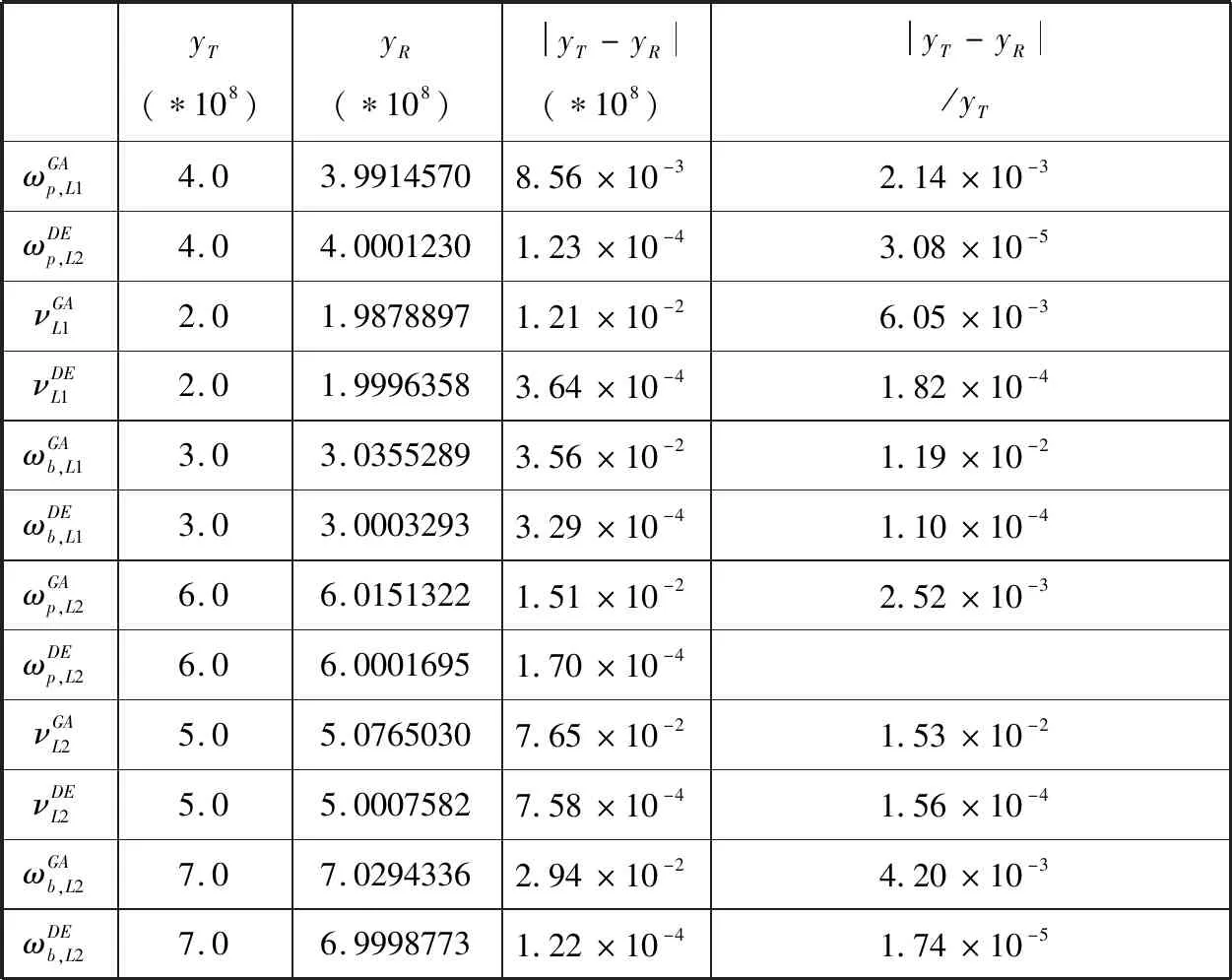
表2 实验二中的等离子体介质参数反演的绝对误差和相对误差

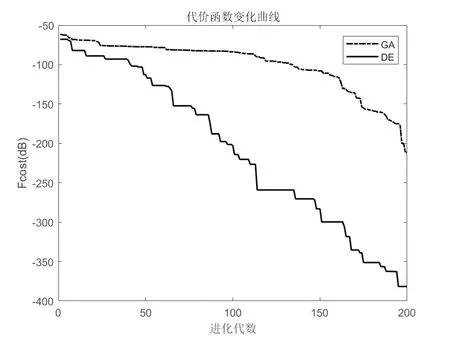
图4 实验二中GA算法和DE算法重构等离子体介质参数时代价函数值随进化代数的变化曲线

实验三，目标等离子体区域为多层非均匀等离子体。在这个实验中，已知等离子体区域的碰撞频率ν=2.0×108和旋转频率ωb=3.0×108，每个离散网格的等离子频率ωp都是未知的。因此，用直接法表示时由式(13)可知an有30个未知量，用立方B样条曲线展开时未知量数等于控制点数Nc，这里选取Nc=5。图5为GA算法和DE算法重构的多层非均匀等离子体介质参数与理论值对比(a)直接表示法，(b)立方B样条展开法，可以看出无论是GA算法还是DE算法，用立方B样条曲线展开法表示参数改进算法都有比直接表示法更好的重构准确度。并且，由图(b)可以看出，DE算法和立方B样条曲线展开结合的改进算法有比GA和立方B样条展开结合的改进算法更好的重构准确度。

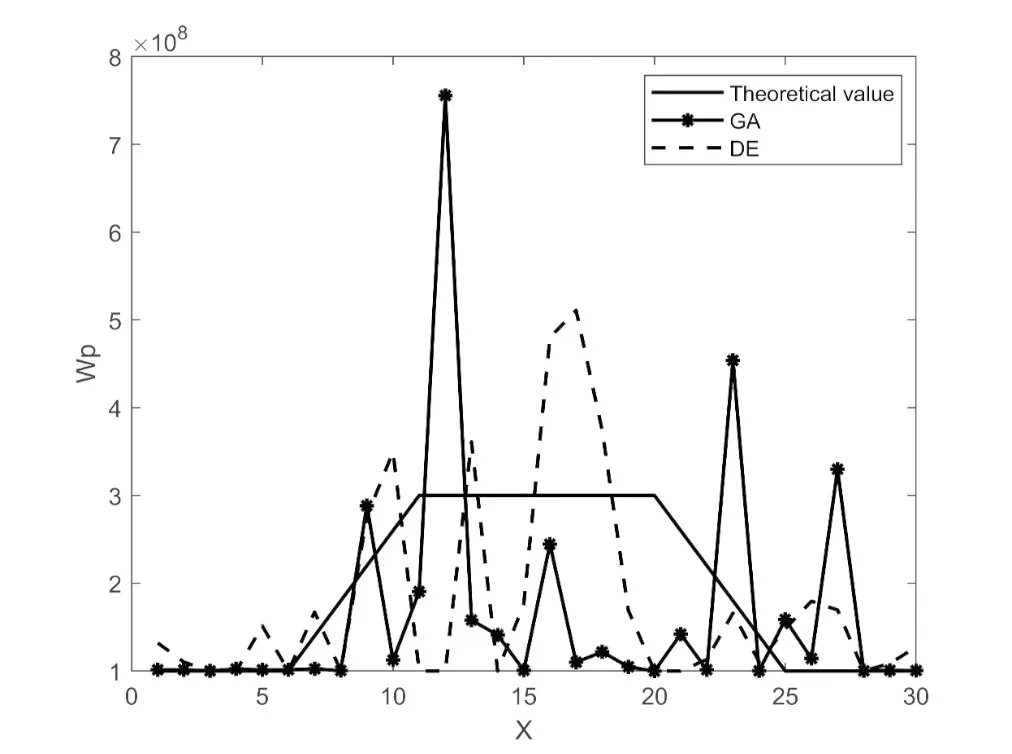
(a)直接表示法

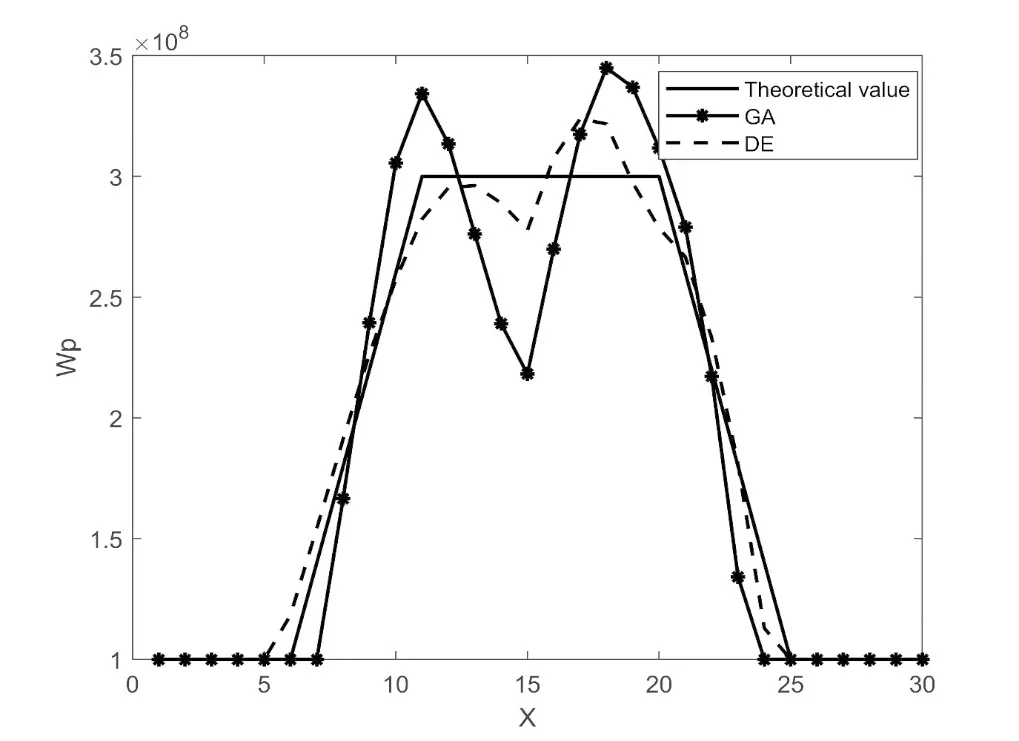
(b)立方B样条展开法图5 实验三中GA算法和DE算法重构的等离子体介质参数与理论值对比

5 结论

本文将等离子体时域正演算法和遗传算法、差分进化算法相结合，研究了非均匀等离子体介质的参数重构。针对有严重病态性的多层非均匀等离子体，提出了用立方B样条曲线展开对等离子体介质参数进行表示，与直接参数表示法对比表明，改进算法有更快的收敛速度和更好的准确度。通过相同条件下GA算法和DE算法对比可以发现，DE算法有比GA算法更快的收敛速度和介质参数重构准确度。