数学实践活动课的教学策略初探

宋明月

(江苏省无锡市惠山区钱桥中心小学 江苏 无锡 214000)

关于“综合与实践”义务教育《数学课程标准(2011年版)》是这样阐述的：“综合与实践”是一类以问题为载体、以学生自主参与为主的学习活动。在学习活动中，学生将综合运用“数与代数”“图形与几何”“统计与概率”等知识和方法解决问题。“综合与实践”的教学活动应当保证每学期至少一次，可以在课堂上完成，也可以课内外相结合。提倡把这种教学形式体现在日常教学活动中。“综合与实践”内容设置的目的在于培养学生综合运用有关的知识与方法解决实际问题，培养学生的问题意识、应用意识和创新意识，积累学生的活动经验，提高学生解决问题的能力。

在现实的数学教育教学活动中，“综合与实践”与“数与代数”“图形与几何”“统计与概率”相比，未能引起广大一线数学教师的足够重视，未能贯穿数学教育的始终，更未能成为培养学生应用意识、创新意识很好的载体。究其原因，不外乎以下几个方面：一是学时不够；二是“综合与实践”中的内容一般不会成为考试的考察点；三是这部分内容教学起来难度大，需要准备的材料多；四是从上到下的重视程度不够，也就不能发挥好这部分内容应有的作用。笔者结合苏教版六年级上册第一单元《表面涂色的正方体》一课，谈谈数学综合实践活动课的教学策略。

1.在观察与操作中，让学生自己发现问题和提出问题

数学老师都知道让学生发现问题和提出问题比解决问题更重要，如何在“综合与实践”内容教学中，让学生发现问题和提出问题？在观察中操作，在操作中观察是有效途径。

《表面涂色的正方体》一课，让学生发现问题和提出问题通过以下三个环节实现。第一环节：观察中思考。先出示一个表面涂色的正方体，每条棱都平均分成2份。如果照图一的样子把它切开，能切成多少个同样大的正方体？每个正方体有几个面涂色？对于这一环节，让学生在观察中思考并得出答案即可。2×2×2=8(个)，能切成8个小正方体，每个小正方体都有3个面涂色。

第二环节：操作中观察。每条棱都平均分成3份，如果照图二这样把正方体切开，能切成多少个小正方体？切成的小正方体中，3面涂色、2面涂色、1面涂色的各有多少个，分别在什么位置？与上一环节相比，虽然每条棱只是从平均分成两份到平均分成3份，但在理解上难度却增加了很多。把孩子们平时喜欢玩的魔方请进课堂，让孩子在拆、拼魔方的过程中边观察，边思考，得出答案：切成小正方体的总个数是27个，3面涂色的是8个，在大正方体的顶点位置，2面涂色的小正方体有12个，在大正方体的棱上，1面涂色的小正方体有6个，在大正方体每个面的中间。

老师适时提问：至少有一面涂色的小正方体的个数是26个，比小正方体的总个数27个少了一个，这少的一个在哪里？它是怎样的？(在大正方体的中心位置，没有面涂色。)

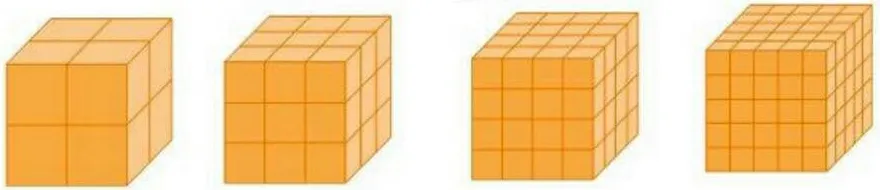
图一 图二 图三 图四

第三环节：观察中分层操作。如果把这个正方体的每条棱平均分成4份、5份、6份……再切成同样大的小正方体，结果会怎样？先观察图三和图四，如果有困难的，可以在图中找一找，分一分，再把结果填入下表，与同学交流。

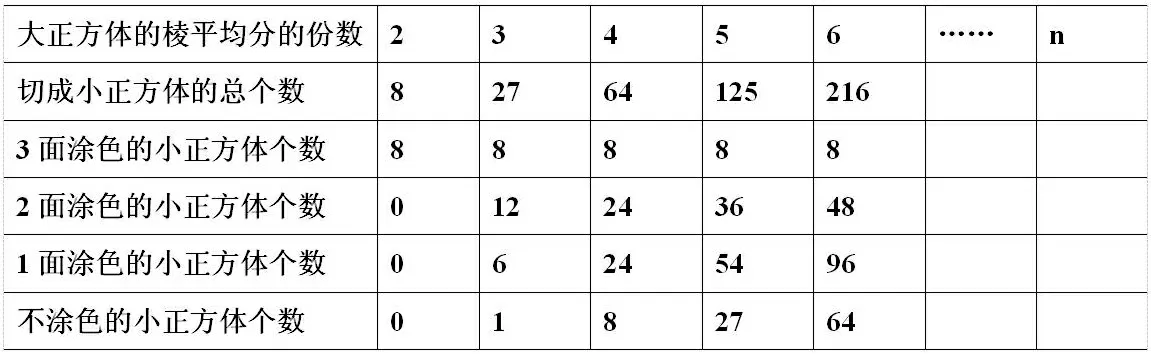
观察填出的表格，你有什么发现？能提出哪些与此相关的问题？建立在观察与操作的基础上，学生提出了如下有价值的问题：

①为什么切成小正方体的总个数越来越多，而3面涂色的小正方体个数都是8个？

②3面、2面、1面、不涂色的小正方体个数与它们所在的位置是否有关系？

③这4种小正方体的个数之间有什么样的联系？

④这4种小正方体的个数能否用含有字母的算式来表示？

2.在想象与推理中，让学生学会独立思考和互助合作

认真听讲、积极思考、动手实践、自主探索、合作交流等，都是学习数学的重要方式。在“综合与实践”领域，独立思考与互助合作显得更为重要。《表面涂色的正方体》一课中，学生提出了很多问题，最后在老师的引导下归纳成上述4个。如何解决这些问题，应根据问题的难度及特点采用不同的教学策略。

问题①为什么切成小正方体的总个数越来越多，而3面涂色的小正方体个数都是8个？是比较单一的，让学生独立思考，结合②问题3面涂色的小正方体都在原大正方体的顶点位置，因为正方体有8个顶点，所以3面涂色的小正方体个数总是8个，与大正方体的棱被平均分的份数无关。

将一个表面涂色的正方体，每条棱平均分成3份、4份、5份、6份……再切成同样大的小正方体，3面涂色、2面涂色、1面涂色、不涂色的小正方体各有多少个？2面、1面、不涂色的小正方体个数与它们所在的位置是否有关系？这4种小正方体的个数之间有什么样的联系？这4种小正方体的个数能否用含有字母的算式来表示？这些问题的解决如果光靠学生的独立思考是比较困难的，要在观察与操作的基础上发挥想象和推理在数学学习中的作用。2面涂色的小正方体，都在棱上，因为正方体都有12条棱，所以2面涂色的小正方体的个数都是12的倍数；1面涂色的小正方体都在每个面的中间，所以个数都是6的倍数。

在有限的课堂教学时空内，更要将学生的独立思考与互助合作结合起来，提高课堂教学的效率。学生的合作过程中合理分工，互相补充，思维上互相启迪，快速高效地完成学习任务，达成教学目标。在“综合与实践”领域，随着年段的增长，这样的合作将会越来越多，学习力得到不断的提高。

3.在比较与归纳中，让学生概括猜想规律并加以验证

《表面涂色的正方体》一课中，学生提出3面、2面、1面、不涂色的小正方体个数与它们所在的位置是否有关系？这4种小正方体的个数之间有什么样的联系？这4种小正方体的个数能否用含有字母的算式来表示？其实学生已经感受到其中存在的规律，并且对这些规律有一定的猜想。这时，应该在师生互动中，概括猜想，总结规律，并加以验证，比较与归纳是有效教学策略。本课所得出的规律主要有以下几条：

①2面涂色的小正方体，都在棱上，因为正方体都有12条棱，所以2面涂色的小正方体的个数都是12的倍数；观察与比较表格中的数据，分别是0、12、24、36、48……如果用n表示大正方体的每条棱被平均分成的份数，2面涂色的小正方体个数可以用(n—2)×12来表示，n—2表示每条棱上2面涂色的小正方体的个数，减去的2表示每条棱的端点位置要去掉2个3面涂色的小正方体。

②1面涂色的小正方体都在每个面的中间，所以个数都是6的倍数。观察与比较表格中的数据，分别是0、6、24、54、96……如果用n表示大正方体的每条棱被平均分成的份数，1面涂色的小正方体个数可以用(n—2)2×6来表示，(n—2)2每个面上1面涂色的小正方体的个数。

③不涂色的小正方体都在原正方体的中心位置，如果不切开是看不到的。观察与比较表格中的数据，分别是0、1、8、27、64……如果用n表示大正方体的每条棱被平均分成的份数，不涂色的小正方体个数可以用(n—2)3来表示。

④这4种小正方体的个数相加应该等于小正方体的总个数。可以用这个方法来检验每种小正方体的个数是否算对，完成并完善表格：

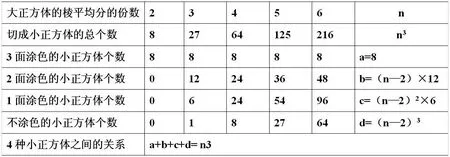
学生得出的猜想是否正确与合理，需要进行验证。推理是数学的基本思维方式，包括合情推理和演绎推理。合情推理用于探索思路，发现结论，演绎推理用于证明结论。上述结论中：a=8，b=(n—2)×12，c=(n—2)2×6，d=(n—2)3，a+b+c+d=n3，后四个需要学生和老师通过举例，用不完全归纳法进行验证，也可以通过字母式之间的关系进行论证，同时规定n的取值范围n是≧2的自然数。

4.在体验与建构中，让学生获得思想方法和活动经验

2011版《数学课程标准》提出了十个核心概念：数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力、模型思想、应用意识和创新意识。前8个是基础，后2个是核心。要让“综合与实践”真正成为培养应用意识与创新意识的载体，就必须注重学生的体验与自我建构，运用所学的数学知识与技能，体会和运用数学思想方法，获得基本的数学活动经验。

《表面涂色的正方体》一课，在师生共同得出规律之后，要让学生回顾探索和发现规律的过程，说说自己的体会，从不同的方面加以总结提升：

①找a，b，c，d四种小正方体时，要注意它们在大正方体上的位置；

②a，b，c三种小正方体的个数与正方体顶点、面和棱的个(条)数有关；

③要把找、数、算等方法结合起来，并根据图形的特征进行思考；

④虽然课本只要我们研究a，b，c三种小正方体的个数，我们觉得不够完整，所以增加了第四种，不涂色的小正方体；

⑤虽然增加的第四种小正方体的个数与正方体顶点、面和棱的个(条)数有关看似没有直接的联系，但是与a，b，c三种小正方体的个数有关，a+b+c+d=n3；

⑥有了a=8，b=(n—2)×12，c=(n—2)2×6，d=(n—2)3，a+b+c+d= n3这5个结论，我们可以检验每种正方体是否数对或算对，对于棱数更多的问题，可以直接运用规律……

学生如此丰富的体会，是今后的数学学习动力，更能转化为数学学习的能力，“综合与实践”确实是培养学生培养应用意识与创新意识的肥沃土壤。