Laplace方程边值问题的五点差分格式
支越
(中国传媒大学信息科学与技术学部,北京 100024)
1 引言
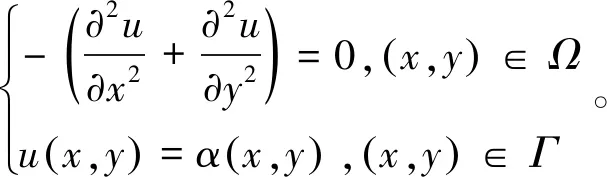
这里δ(x,y)≥0。
若边界Γ上不同部分满足不同类型的边界条件,则为混合边值问题。假设α(x,y),β(x,y),γ(x,y),δ(x,y)为定义在边界Γ上的光滑函数。
本文用五点差分格式建立Laplace方程边值问题的差分方程组,具体步骤如下:
(1)将区域Ω进行网格剖分。
(2)对区域Ω上的内点建立差分格式。
(3)对区域Ω上边界条件的处理。
为简便讨论,取区域Ω为正方形区域进行均匀正方形网格剖分。
2 在差商代替导数的方法下建立差分格式
2.1 区域Ω上内点的差分格式
对内网格点(i,j),1≤i≤N-1,1≤j≤N-1,有(N-1)×(N-1)个内点。
内点列出的差分格式:-(ui,j+1+ui,j-1+ui+1,j+ui-1,j-4ui,j)=0。
2.2 区域Ω上的边界条件的处理
对于第一类边界条件,u(x,y)=α(x,y),∀(x,y)∈Γ,将uij=αij直接代入差分方程中 。
对于第二、三类边界条件,在正方形区域Ω四个边界外侧的一个步长h处,各增设一排虚网点,用中心差商逼近边界条件中的法向导数,在四个边界点上单独列出差分方程。
例如,在左边界(0,j)(0≤j≤N)的左侧增设(-1,j)(0≤j≤N),用中心差商逼近边界条件中的法向导数
通过在左边界增设一排虚网点,以(0,j)为内点建立五点差分格式,与内点(i,j)列出的差分格式联立,从而消去了虚网点(-1,j)上的未知量u-1,j。
根据上述方法,以Laplace方程的第二边值问题为例,列出其在上、下、左、右边界的差分格式。
下边界差分格式:-2ui,1-ui+1,0-ui-1,0+4ui0=2hβi0,i=1,2,…,N-1
上边界差分格式:-2ui,N-1-ui+1,N-ui-1,N+4uiN=2hβiN,i=1,2,…,N-1
左边界差分格式:-2u1,j-u0,j+1-u0,j-1+4u0j=2hβ0j,j=1,2,…,N-1
右边界差分格式:-2uN-1,j-uN,j+1-uN,j-1+4uNj=2hβNj,j=1,2,…,N-1
角点(0,0),需要用到左侧的虚网点(-1,0)和下侧的虚网点(0,-1),由左边界、下边界和内点的差分格式联立,消去未知量u-1,0和u0,-1,(0,N),(N,0)和(N,N)类似处理。
角点(0,0),-u1,0-u0,1+2u00=2hβ00
角点(0,N),-u0,N-1-u1,N+2u0N=2hβ0N
角点(N,0),-uN,1-uN-1,0+2uN0=2hβN0
角点(N,N),-uN,N-1-uN-1,N+2uNN=2hβNN
3 在积分插值法下建立差分格式
3.1 区域Ω上内点的差分格式
对内网格点(i,j),1≤i≤N-1,1≤j≤N-1,区域Di,j为:

对区域Di,j分段积分得-([u]i,j+1+[u]i,j-1+[u]i+1,j+[u]i-1,j-4[u]i,j)≈0。
3.2 区域Ω上的边界条件的处理


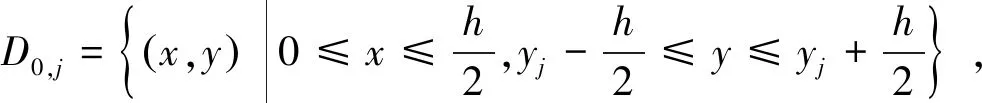

得-[u]1,0-[u]0,1+2[u]0,0≈2hβ00。
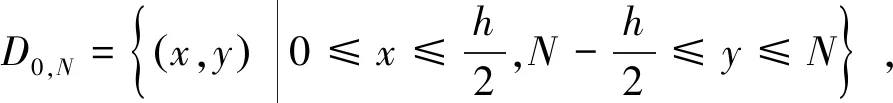

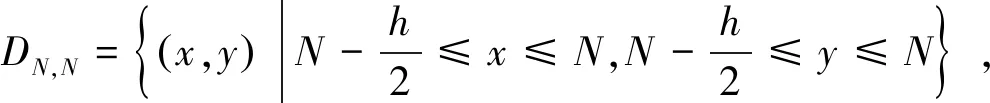
4 差分方程组
Laplace方程第二边值问题的差分方程组如下:
5 结论
本文用差商代替导数的方法与积分插值法,对Laplace方程第二边值问题建立了五点差分格式。对边界条件的处理上,通过增设虚网点,用中心差商逼近法向导数,但这种方法是不严谨的,因为Laplace方程在边界点上五点差分格式不一定成立。不过实际应用方便,它列出的边界点差分格式与积分插值法是一致的。积分插值法的优越性是容易在边界点上建立差分格式,选定积分区域,进行分段积分,这避免了在边界上逼近法向导数,这样处理既方便又减少误差,特别是当边界不平行于坐标轴时,更显其优越性。

