基于遗传算法的水下传感器网络节点部署算法研究*

金合丽,刘半藤,陈 唯,凌家顺

(浙江树人大学信息工程学院,杭州 310015)

水下无线传感网络UWSN(Underwater Wireless Sensor Networks)是将低能耗、通信距离受限的节点部署在指定水域中,利用节点的自组织能力自动组网,对指定区域内的信息进行采集并完成相应的数据收集和整理[1]。UWSN在海洋资源勘探、海洋环境监测以及海洋军事领域有广泛且重要的用途,已经引起工业界、学术界以及军事界的极大关注。近年来,随着各国发展海洋经济热潮兴起,UWSN已经成为无线传感器网络的热点新兴研究领域之一。

区别于传统二维无线传感网络2D-WSN(Wireless Sensor Networks),UWSN需要监测三维水域环境。由于水下环境复杂多变且仅能依靠衰落较快的声波信号传输信息、节点成本高、网络能耗大等原因,许多2D-WSN的方法并不适用于UWSN[2]。由于水下节点部署研究直接关系到网络的节点能量、通信带宽、监测信息的准确性,成为UWSN众多研究方向的首要待解决问题。

近年来,有不少学者针对UWSN节点部署开展广泛而深入的研究。由于水下传感器节点成本高,节点数量优化往往成为UWSN节点部署的首要考虑目标[3]。目前,对于UWSN节点部署方案可以归纳为以下两类:在满足一定条件的情况下,使得网络所需节点数量最小化;或者在网络节点数量不超过某定量时,使得网络性能达到最优化。网络整体覆盖率与节点间连通率也是网络构建的重要指标[4-5]。例如,赵敏华等人提出了一种非均匀简单立方格节点部署算法。该算法在确保网络覆盖率的情况下,考虑水声网络能耗特点,可有效降低网络能耗,提高网络寿命[6]。田祥宏以网络覆盖率和节点分布均匀度为目标函数,提出了一种基于黏性流体算法的优化部署方案,并运用鱼群优化算法进行求解[7]。李世伟等人提出一种基于潜艇深度的节点部署算法,通过潜艇深度信息的概率模型设计节点的活动状态,提高覆盖率[8]。胡照鹏等人提出一种基于矩形分区覆盖的节点确定部署策略,采用矩形分区覆盖部署方式减少部署节点的数量并减少路由跳数[9]。郭秀明等人提出一种基于网格扫面实现确定性目标点覆盖的节点部署方法,为了选择合适的位置放置节点将目标区域划分成若干正方形网格并提出一种评价标准,实现最少的节点对目标覆盖[10]。高德民等人对无线传感器网络随机分布模型的覆盖问题进行研究,提出数学模型来量化节点密度、感知半径和面积覆盖率的关系,有效增加覆盖面积并减少重覆盖[11]。通过文献综述,可以发现大部分UWSN的节点部署方案在计算覆盖率指标时采用感知模型,将网络离散成格点,以被感知格点数量所占格点总数比例记为网络覆盖率。这样的计算方法虽然简单,但容易出现覆盖空洞,如图1所示。

图1 覆盖算法中的覆盖空洞示意图

图1中,虽然正方形区域的四个格点被两个传感器节点所覆盖,但显然传感器节点并不能覆盖整个正方形区域,存在“覆盖空洞”。这也是很多文献关于UWSN覆盖率算法存在的不足之处。很多文献在网络连通性指标上并没有讨论,没有给出连通性的计算方法。本文从UWSN部署节点数量最小化角度出发,对传统的覆盖算法进行修正,以整体网络覆盖率和节点连通率两项指标作为约束条件,建立整数非线性模型求解节点优化部署方案。

1 节点模型

通常,UWSN由基站节点与普通传感器节点两种类型的节点构成[12]。其中,基站节点(Sink)负责接收来自普通传感器节点传来的监测海域的数据信息;普通传感器节点负责采集覆盖海域内的信息并将其以多跳传输的形式传送到Sink节点。为方便讨论问题,假设UWSN每个传感器节点具有固定的覆盖半径Rc和传输半径Rn,其结构如图2和图3所示。通常,Sink节点的传输半径要远大于普通节点的传输半径。

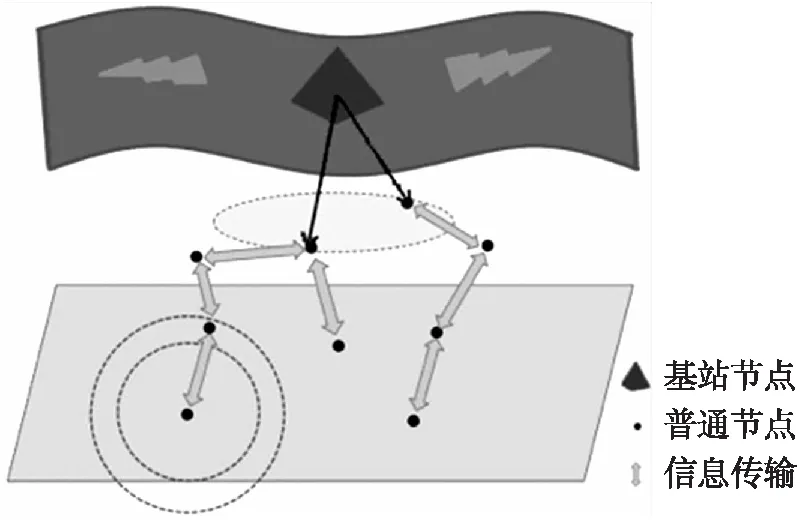
图2 水下传感器网络结构示意图

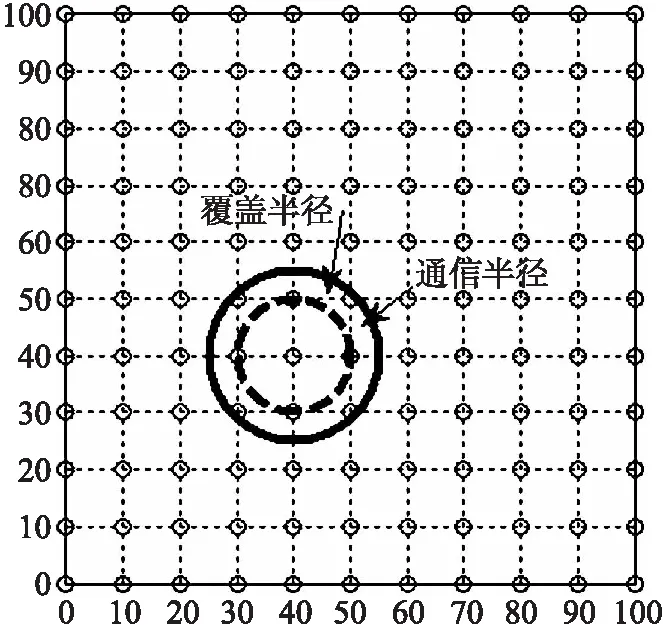
图3 节点通信半径与覆盖半径说明示意图

每一个普通传感器节点都可以采集覆盖半径内的数据信息,并将采集获得的数据信息转发给距离其传输半径内的其他节点。

由于UWSN所需探测的三维环境复杂多变,为便于讨论节点部署问题可将所探测的长方体区域划分成较小规格的网格。例如,一个规格为K×M×L的长方体网络,以“1”为步长进行离散化处理将会形成N=(K+1)×(M+1)×(L+1)个格点,{K,M,L}∈Z+。网络中的每一个格点位置都可以用三维坐标(x,y,z)(x=1,2,…,K+1;y=1,2,…,M+1;z=1,2,…,L+1)进行唯一标识。假设在文中讨论最优化网络节点部署时,传感器节点只能部署在格点。对于一个由N个格点构成的UWSN,可以引入一个0-1决策矩阵G=(gxyz)(K+1)×(M+1)×(L+1)以表示是否在格点位置(x,y,z)放置传感器节点,矩阵元素含义如下:

因此,最优节点部署问题可以归结为求解最优决策矩阵G。

UWSN中的节点采用声纳方式相互通信。UWSN环境中,节点的能耗可以参考以声波为媒介的UWSN数据通信能耗模型[13-14]。节点发送数据能耗Esend、节点接收数据能耗Erec、数据融合的能耗Eintg计算方式如下所示:

其中,l表示数据包的长度,Ps表示节点可以接收到单位数据所需的最小功率,d表示发送节点和目的节点之间的距离,Pr是常数,Edate表示数据融合能耗,λ为能量扩散因子。由于水中信号呈现球形扩散,通常取λ=2[15]。α表示吸收参数,由载波频率f决定。

2 连通性指标

当传感器节点采集区域信息后,将以节点间多跳传输的形式传递到水面的Sink节点。可以引入一个六维的连通矩阵T=(txyz·opq)[(K+1)×(M+1)×(L+1)]×[(K+1)×(M+1)×(L+1)]表示位于(x,y,z)与(o,p,q)的两个传感器节点之间的连通状况。由于每个传感器的位置可以由一个三维坐标确定,故连通矩阵是六维矩阵。在指定的某种节点部署方案G=(gxyz)(K+1)×(M+1)×(L+1)下,位于(x,y,z)与(o,p,q)的两个传感器节点间的一跳连通状况计算方法如下:

txyz·opq=

当位置(x,y,z)与位置(o,p,q)都放置传感器节点(即gxyz=gopq=1),且两点之间的距离小于传输半径Rn时,说明两个传感器节点间可以相互传输信息,即认为此两个传感器节点是连通的。

假设UWSN网络中Sink节点标号为(sx,sy,sz)。由于海域中的任意一个普通传感器节点都需要将监测获得的信息传送到Sink节点。因此,对于位置(x,y,z)的传感器节点而言,是否与Sink节点连通可以由下式计算获得:

由于UWSN中所有的传感器节点都能够将采集的信息传输到基站Sink,应该符合如下约束条件:

上式表明与Sink节点连通的传感器节点数量等于UWSN网络部署的节点总数。此约束条件可确保网络中的每个节点都可以将信息传输至Sink。

3 覆盖率指标

为了改善“覆盖空洞”问题,本文将网络覆盖问题转化为KML个正方体的覆盖问题。某个正方体的左下顶点(i,j,h),i=1,…,K;j=1,…,M;h=1,…,L,该正方体的顶点集合可以表示为:Sijh={(i,j,h),{i,j,h+1},{i,j+1,h},{i,j+1,h+1},(i+1,j,h),{i+1,j,h+1},{i+1,j+1,h},{i+1,j+1,h+1}}。因此,每一个正方体都可以用一个顶点集合唯一标识,如Sijh。

如果存在一个传感器节点距离UWSN中某正方体八个顶点的距离都小于覆盖半径Rc,则可以认为该正方体可以被传感器节点有效覆盖。传感器节点覆盖小正方体的情况可以用一个0-1覆盖矩阵F=(fxyz·ijh)((K+1)×(M+1)×(L+1))×(K×M×L)表示。位于格点(x,y,z)的传感器节点是否能够覆盖正方体Sijh可以计算如下:

若UWSN中的正方体Sijh可以被至少一个传感器节点完整覆盖,则认为该正方体可以被覆盖。在覆盖矩阵F的基础上,某个正方体被覆盖的情况可以用一个新的0-1覆盖矩阵FF=(ffijh)(K×M×L)表示。

因此,在某种节点部署方案(G)下,网络的覆盖率Cov(G)可以用被覆盖正方体体积占整体网络体积百分比进行表示,计算方法如下:

因此,以部署传感器节点数量最小化,要求网络覆盖率达到α以上,优化模型可以表达如下:

4 算法设计与数值仿真

Step1设定网络初始参数,如网络区域范围、Sink节点位置、离散化格点边长、初始种群数量、迭代最大代数、GA算法交叉概率、GA算法变异概率等基本参数。

Step2计算并判断种群内个体是否符合覆盖范围约束要求、连通度约束要求。如果种群内个体不符合此两项约束条件,随机生成个体并重新判断,直至使得种群内个体数量等于初始种群数量。

Step3计算种群内各个体的适应度函数Fitness1(Ri),将种群个体按照适应度函数值从大到小排序,选择前10%的种群个体直接复制到下一代的种群。根据交叉准则,从原始种群中按照适应度大小顺序进行两两交叉,并将交叉后的结果放至下一代种群。根据变异准则,从原始种群中按照适应度大小顺序进行变异,并将变异后的结果放至下一代种群,直至使得下一代种群数量等于初始种群数量。检查下一代种群数量是否等于初始种群数量。如果不足,则随机生成个体加入下一代种群。

Step4检查是否到达最大代数或者满足算法结束条件。如果满足结束条件,则输出网络最少节点数量Mopt。如果不满足结束条件,则跳转至Step 2。

为评价本文所提出的算法效果,本文采用MATLAB软件进行数值仿真。针对一个60 m×60 m×60 m海域部署传感器节点。以5 m为步长离散为13×13×13的格点。在GA中,设定迭代代数最多为30,初始种群大小为80,交叉概率为80%,变异概率为50%。

首先,讨论针对不同的网络覆盖率要求,在不同的覆盖半径下,网络最优解点数量算法收敛如图4、图5所示。

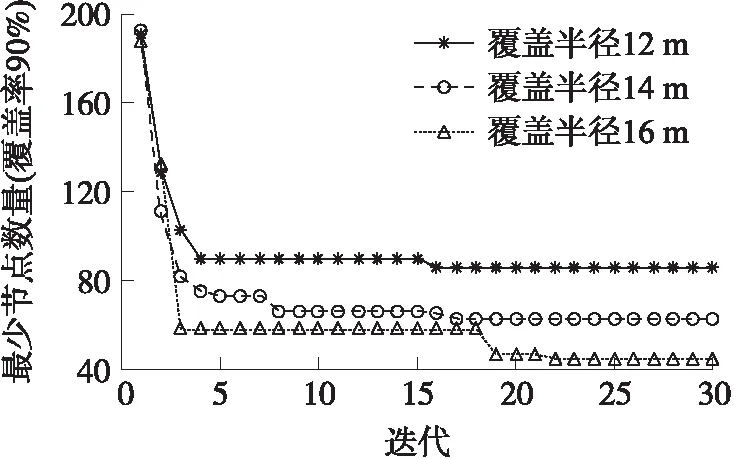
图4 网络覆盖率90%下,遗传算法收敛图

图5 网络覆盖率100%要求下,遗传算法收敛图

对比不同的覆盖率要求,可见在100%覆盖率要求下需要部署的网络节点数量要远大于在90%覆盖率要求下部署的网络节点数量。例如,在覆盖半径为16 m时,实现网络100%覆盖需要的节点数量为75个,而实现网络90%覆盖仅需要的节点数量为47个。而在现实情况下,传感器节点成本昂贵,而100%覆盖并不是必须的。

讨论不同覆盖半径下,不同覆盖率要求所需部署最少节点数量如图6所示。

从图6可以发现:随着覆盖半径增加,所需部署节点的最少数量呈现较为明显的下降趋势。由于覆盖半径增加,扩大单节点的覆盖范围,从而降低网络节点数量。

图6 不同覆盖半径下,最少部署节点数量变化趋势图

假设每个节点的初始能量为10 J,对比本文采用的正方体覆盖方法与传统的感知覆盖算法得到的节点部署方案。定义网络中节点能量最低的节点为瓶颈节点,瓶颈节点能量随传播轮数的变化趋势如图7所示。

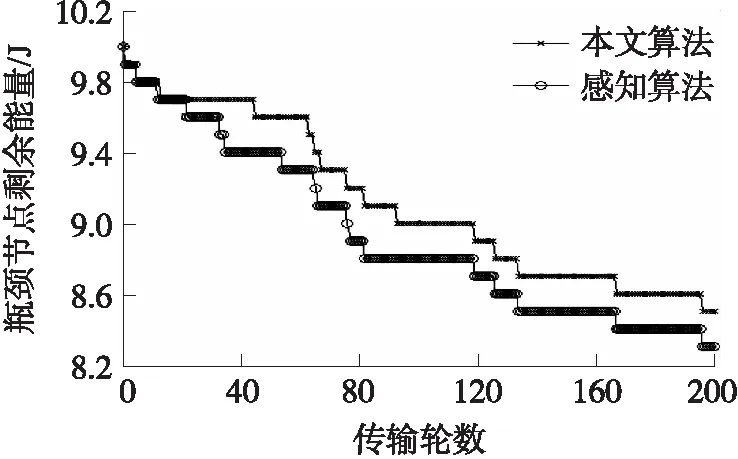
图7 网络中瓶颈节点能量变化趋势图

从图7可以发现,相较于传统的感知覆盖部署方案,本文提出的部署方案可以降低网络瓶颈节点能耗,从而提高网络生存时间。

5 结束语

本文从UWSN节点数量最小化角度出发,同时考虑网络连通性与覆盖性两项指标建立优化模型,提出了一种基于遗传算法的节点优化部署方案。相比与传统覆盖算法,本文算法能够有效地降低覆盖空洞,提高网络覆盖率,提高网络生存时间。