一种互补耦合型电磁感应式直线位移传感器的研究*

翁道纛,汤其富,彭东林,谷星莹

(重庆理工大学机械检测技术与装备教育部工程研究中心,重庆 400054)

直线位移传感器是一种重要的位移测量元件。其作为直线位移反馈元件在工业领域有着广泛的应用。目前在工业领域中常用的直线位移传感器有光电型、电场型以及磁场型三大类传感器[1-2]。目前光电型中典型的代表有直线光栅传感器和激光干涉仪;在电场型中容栅位移传感器应用较为广泛;在磁场型方面有感应同步器和磁栅位移传感器。光电型位移传感器相较于其余两种能够达到较高的精度,适合应用于精密位移测量,但是这类传感器的制造工艺要求较高,工作性能易受环境变化的影响;电场型位移传感器如容栅等,测量精度高,但是量程偏小,相较于其余两类位移传感器更适合小位移测量[3];磁场型位移传感器的制造成本低,能够实现较大的量程,但测量精度偏低,且其测量精度易受到外界条件的影响。直线磁场式时栅位移传感器是一种典型的磁场型直线位移传感器,其在已有的磁场式角位移时栅传感器的基础上发展而来[4-5],能够实现较大的测量量程,目前直线磁场式时栅位移传感器按结构分主要有两类,即绕线式和平面线圈式直线时栅[6]。由于两种直线时栅结构上的限制,导致传感器的几何尺寸误差和机械装配误差对测量精度的影响较大。由此,针对上述问题开展对直线时栅位移传感器的结构改进研究。

1 传感器基本结构

本文提出的直线位移传感器,是基于文献[6]中的“主动约束磁场型直线位移传感器”而设计。主动约束磁场型直线位移传感器的结构如图1所示,图1显示该传感器为单面耦合型,即动尺只在定尺一侧安装。动尺通过在被测位移方向相对于定尺移动,周期性地改变激励线圈与感应线圈的磁场耦合,使感应线圈输出与被测位移相关的信号。为了保证该传感器的测量性能,其动尺和定尺之间的间隙和平行度需要保持在一定范围内。传感器的测量性能越高,对动尺与定尺之间的间隙和平行度的约束越高。

图1 单边耦合型直线时栅位移传感器的基本结构

单面耦合型的直线位移传感器[7]在实际的使用中,会因为安装误差及外源振动导致动子和定尺之间的间隙变化,从而导致传感器输出信号发生不稳定变化,最终使得传感器的测量精度降低。因此,本文提出一种互补耦合型电磁感应式直线位移传感器,如图2所示,有助于弥补图1所示传感器的不足。

图2(a)所示的直线位移传感器主要由定尺D1和动尺D2组成组成。定尺包含G1组和G2组激励线圈,及I1组和I2组感应线圈,如图2(b)、(c)所示,激励线圈和感应线圈均为平面线圈,其中,激励线圈为正弦形线圈,感应线圈为矩形线圈。G1组和G2组激励线圈在定尺上周期分布,在被测位移方向上二者的起始点相差1/4周期。动尺为矩形齿状导磁体,并且关于中间槽对称,在被测位移方向上齿的宽度等于激励线圈周期的一半,其结构如图2(d)所示为动尺的等轴测图和侧视图。动尺通过中间槽跨于定尺安装,如图2(a)和2(b)所示,在定尺两边的动尺结构完全相同。在动尺齿所处位置,激励线圈和感应线圈的磁场耦合程度比其他位置大。当动尺与定尺之间一侧的间隙增加或减小时,另一侧的间隙减小或增加,而两侧激励线圈与感应线圈的耦合程度随之一侧增大或减小、另一侧减小或增大。

图2 互补耦合型直线位移传感器结构

2 直线时栅位移传感器测量原理

互补耦合型直线位移传感器测量原理基于“时空坐标转换理论[8-10]”,即将定尺视为静坐标系,定尺上的时变磁场[6]视为动作标系,而动子处于匀速或变速状态,由此动子的位移量ΔX就可以转换为动子与定坐标系上固定的参考点间的时间差ΔT来表示,那么位移量ΔX就可以表示时间差ΔT与动作标系的速度V的乘积,即ΔX=ΔT×V,而后将运动坐标系的速度V用静坐标系上的等空间间隔ΔS和固定的周期时间T0表示,即V=ΔS/T0,由此ΔX可表示为ΔX=ΔT×ΔS/T0,当ΔT为脉冲计数时间时可以求得动子位移量ΔX。

传感器具体工作方式如下所述,测量动子位移量即通过动子在感应线圈上产生的感应电信号的相位变化量来实现增量位移测量,如图2中所示,在G1组和G2组激励线圈中通入两组激励电信号,即在G1组线圈中通入激励信号e1(t)=Asin(ωt)和在G2组线圈中通入激励信号e2(t)=Acos(ωt),当动子相对于定尺在测量方向上移动时,动子与定尺间将产生4种磁通[11-12]:

(1)

(2)

(3)

(4)

式中,W为激励线圈的正弦结构的周期长度,x为动尺的位移变化量,Δh为激励线圈正弦幅值。其中磁通φ1(t,x)和φ2(t,x)由激励e1(t)产生,磁通φ3(t,x)和φ4(t,x)由激励e2(t)产生,所以将式(1)～式(4)分别代入式(5)～式(8),并将φ1(t,x)和φ2(t,x)合并,以及φ3(t,x)和φ4(t,x)合并,可以得到两相交流激励分别产生的感应电动势[11-12]为:

(5)

式中,k′为常数,其中sin(ωt)和cos(ωt)是一对时间正交的函数,sin(2πx/T)和cos(2πx/T)是一对空间正交的函数。单侧感应线圈产生的感应电动势[11-12]由式(5)与式(6)叠加得到,如式(7)所示。

由于本传感器的设计采用了双边传感的设计,并将两侧动尺相互串联,故两侧感应线圈产生的总感应电动势[11-12]为:

由式(8)可知,当动尺相对定尺产生位移变化时,感应信号的幅值不变,相位将随着位移的变化而变化。将产生的感应信号与同频率的参考信号相比较,两者之间的相位差也随位移的变化而变化,故可根据二者的相位差得到动尺相对于定尺的位移量。假设动尺相对定尺的位移量为x时,感应信号与参考信号过零点时刻的时间差为Δt,则时间差与动尺相对于定尺的位移量之间的关系[11-12]为式(9):

式中,X为周期T对应的位移量,n为传感器在测量范围内的变化周期数。

3 传感器的模型和仿真

基于图2所示的传感器结构,根据场式时栅基本结构建立互补耦合型直线位移传感器的三维模型[13-14]。其具体构建步骤如下:首先,通过三维软件建立了传感器定尺基体、正弦结构的激励线圈、矩形结构的感应线圈和动尺的三维模型,最后将传感器三维模型导入有限元仿真软件建立传感器有限元仿真模型[15],并进行了仿真实验。传感器模型的仿真参数设置如表1所示。

表1 传感器仿真模型的参数设置表

如表1中所示参数,一组正弦激励线圈由两个首尾相连的正弦线圈组成,这两个正弦线圈在相位上差半个周期(这两个参数均指几何尺寸上的相位和周期),因此激励线圈正弦结构幅值即为每个正弦线圈的幅值大小。此外,传感器信号处理电路中的高输入阻抗放大器在连接感应线圈时,感应线圈中有一个小电流,因此为了和上述电路状态相匹配,这里将感应线圈的直流阻抗取较大值,故将其值设为25 MΩ。

中共中央纪律检查委员会和国家监察委员会之所以对高等院校腐败现象进行专项调查处置，就是因为高等院校许多人员不是国家公职人员，但是，他们有非常大的社会和学术影响力，可以利用自己的影响力从事腐败交易活动。中央纪委和国家监察委员会对高等院校的腐败问题进行深入调查，就是要透过高等院校这个特殊的切口，让人们了解影响力腐败的社会危害性。

仿真实验包括单边耦合型和互补耦合型传感器模型的仿真,并对两种模型的仿真结果做了分析对比。对于单面耦合型的传感器模型,分别做了动尺与定尺间隙为0.4 mm和0.6 mm的实验;相应地,对于互补耦合型的传感器模型,分别做了动尺与定尺间隙为(0.4 mm,0.4 mm)和(0.2 mm,0.6 mm)的实验。通过仿真动子在一个激励线圈正弦结构周期内的位移变化得到如上述感应线圈仿真信号,图3、图4所示为单边耦合型结构感应信号仿真结果图,图5和图6所示为互补耦合型结构感应信号仿真结果图。

图3～图6中横坐标表示仿真时间为0～30 μs,纵坐标表示感应线圈上的感应信号,图3和图4中单位为μV,图5和图6中单位为mV,图中的每条感应信号曲线代表动子在移动方向上空间位置移动1 mm的感应信号,每张图中各有16条感应信号曲线。

单边耦合型结构仿真结果分析:对比图3和图4中的单边感应信号可知,单边间隙的扩大使感应信号产生幅值和相位上较大程度的畸变,且产生的信号强度较弱,大小为微伏级别,理论上图中的每条曲线应该等间隔排布,但由图中曲线相位上的不规则排布可知,通过感应信号相位变化测量动子位移量会出现较大偏差,感应信号幅值上的不稳定同样也会造成位移测量值的跳动和误差。

互补耦合型仿真结果分析:如图5和图6所示的感应线圈的仿真信号可知,感应线圈产生的感应信号幅值和相位上畸变程度得到了明显的改善,图中各曲线的相位分布较为均匀,双边间隙在一定范围内变化时,产生的感应信号曲线的幅值和相位没有发生明显的畸变。

图3 单边0.4 mm间隙感应信号

图4 单边0.6 mm间隙感应信号

图5 双边间隙分别为0.4 mm和0.4 mm感应信号

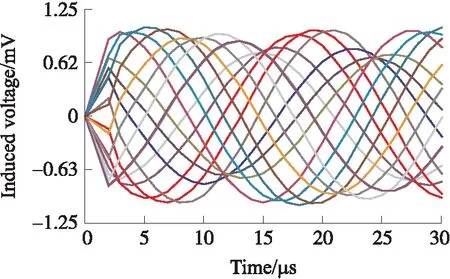
图6 双边间隙分别为0.2 mm和0.6 mm感应信号

如图7所示为定尺两边与动尺间隙分别为0.4 mm和0.4 mm、0.2 mm和0.6 mm的感应磁场信号相位随着动尺位移而变化的仿真图,图7(a)中所示为双边间隙分别为0.4 mm和0.4 mm的对称结构传感器感应信号相位变化仿真图,图7(a)中所示为双边间隙分别为0.2 mm和0.6 mm的对称结构传感器感应信号相位变化仿真图,感应信号的相位变化Δψ随着动尺的位移Δx而均匀变化,且每当动尺移动一个位移Δx感应信号的相位也相应地变化一个Δψ,结合图3～图6可知,当动尺与定尺间隙变化时对该对称结构的感应信号相位的不良影响远小于单边结构。综上所述,采用该对称式结构的直线位移传感器产生的感应信号的强度相较于单边结构有了较大的提高,因此在理论上,采用对称结构能够减小动子和定尺之间的间隙变化带来的测量误差,并有效提高测量精度和稳定性。

图7 互补耦合结构的传感器模型的感应信号相位变化

4 传感器的实物实验验证

用于实验验证的传感器样机的定尺采用PCB(Printed Circuit Board)工艺制造,动尺采用45钢制造。定尺PCB总长度为600 mm,其线圈布线图如图8所示,PCB共4层,其上集成了G1组激励线圈和G2组激励线圈,共有72个周期,周期长度为8 mm,I1和I2为回形感应线圈。

图8 传感器样机定尺PCB布线图

为了验证仿真分析结果的正确性,设计了一套实验装置及测试传感器样机,传感器测试平台如图9所示。该测试平台有六部分组成,分别为①动子及定尺夹具,②直线光栅,③直线导轨,④传感器信号处理板,⑤运动控制板,⑥光学平台,以及⑦安装有传感器数据采集程序的电脑。光栅测头和动子夹具用螺钉固定在直线导轨的运动构件上,并跟随运动构件一齐运动。如图10为传感器样机在测试平台上的侧视图,图中显示了传感器样机动尺与定尺的安装方式。动尺通过顶部螺丝固定于动尺夹头;定尺由如图所示的定尺基体通过挤压方式,以垂直方式固定于定尺基体中。

图9 对称式直线式时栅测试实验台

对互补耦合结构传感器样机进行测试,以测试平台中的光栅为测量基准,获取传感器样机的测量误差。进行第1次测试时(仅运动了100 mm),发现传感器样机的测试误差异常之大,达到了毫米级,如图11所示,为传感器样机在100 mm位移内的误差曲线。

图10 传感器样机在测试平台上的侧视图

图11 测试1,在100 mm位移内测量误差

由图11中数据可知,误差具有规律性,误差周期与激励线圈的周期长度(8 mm)具有相关性。如图12显示了位移为8 mm的误差曲线。由该误差曲线可知,传感器样机的误差有明显的一次成分。

图12 测试1,在8 mm位移内测量误差

在利用示波器观察感应线圈的输出信号时,发现当动尺被移去后感应线圈仍有较大的信号,如图13(a)所示。由文献[6]可知,该信号会引起图13所示误差曲线中的1次成分。为了消除该信号对传感器样机测量精度的影响,在定尺上附近固定一个形状尺寸及材料与动尺完全相同的导磁体(下文称其为校正动尺)。通过调整校正动尺与定尺间的间隙,及其在被测试位移方向的位置,可使感应线圈产生与图13(a)所示信号大小相等、相位相差180°的信号,从而抵消图13(a)所示信号。最终,通过调整校正动尺的位置,图13(a)所示信号的被大幅抵消,抵消结果如图13(b)所示。

图13 无动子条件下校正动尺对传感器样机的调节效果

采用了校正动尺后,传感器样机的测试误差大大减小,如图14和图15所示,修正后一个重复结构周期内的误差为±50 μm,相比未修正前的误差有了明显的减小。由于传感器本身的结构特性,使得传感器可以实现较大的量程,矫正动尺在测量方向的长度较小,因此将校正动尺置于定尺的一端进行残余信号的消除不会影响传感器的正常位移测量。

图14 测试2,在150 mm位移内测量误差

图15 测试2,在8 mm位移内测量误差

为了和所提出的互补耦合结构形成对照本文对单边耦合结构传感器进行实验。由于未经过校正动尺修正的传感器测量误差太大不适合作为互补耦合结构的实验参考,由此利用校正动尺对单边耦合结构进行了误差修正,如图16和图17所示分别为修正后的单边耦合结构传感器在0～100 mm内的位移测量误差和0～8 mm内的位移测量误差:

图17 测试3,在8 mm位移内测量误差

由图16和17可知经过校正动尺修正后的单边耦合结构传感器的在100 mm内的测量误差以及在8 mm内的误差,由图17可知经过修正后一次误差任然占主要成分。单边耦合结构的误差测量结果远大于修正后的互补耦合结构传感器的对应测量误差,因此可知互补耦合结构在减小直线传感器测量误差方面要优与单边耦合结构。

为了验证本文所提出的互补耦合结构在减小传感器装配误差对传感器测量精度的影响,对传感器样机在动尺和定尺之间不同的间隙情况下进行测试,如表2所示为经过校正动尺修正后的互补耦合结构的不同动子和定尺间隙下的测量误差值,其中设动尺与定尺两侧的间隙为A面间隙和B面间隙,为了和互补耦合结构相对照,本文对经过校正动尺修正后的单边耦合结构传感器也进行了相同的误差实验,实验结果如表3所示。

由表2所示,可以观察到传感器在一个机械周期内的测量误差随着A面间隙和B面间隙之和的增加而增大,而当A面间隙和B面间隙之和保持不变时,传感器的测量误差变化较小。另外,A面间隙和B面间隙相等,且二者同时增加时,传感器样机的测量误差增加。根据表3中的实验结果可知,单边耦合结构传感器测量误差随着间隙的增大而显著增加。

表2 互补耦合结构不同动尺和定尺间隙下的测量误差

表3 单边耦合结构不同动尺和定尺间隙下的测量误差

根据上述实验结果和分析,互补耦合结构的传感器动尺与定尺之间的间隙受外界因素影响发生变化时,只要两侧的间隙之和不变,传感器的测量性能仅产生微小变化,由此可推论出互补耦合结构相较于单边耦合结构传感器在测量误差方面具有较强的抵抗间隙变化影响的性能,即互补耦合结构能够防止传感器装配误差对传感器测量精度的影响。

5 结束语

针对直线位移传感器中单面耦合结构潜在的不足,本文提出了一种互补耦合型电磁感应式直线位移传感器。通过对动尺结构及安装方式、定尺安装方式的改进,该传感器可以有效抑制动尺与定尺间的间隙变化、平行度差等装配问题对测量性能的影响,从而减小对传感器安装和运行轨迹直线度的要求。对于该传感器,文中介绍了其仿真实验和实物实验。两种实验结果均表明,本文提出的互补耦合结构,对于改善电磁感应式直线位移传感器的测量精度,及提高其抑制安装问题所带来影响的能力均有重要意义。

此外,由于传感器样机最终的测量误差具有较好的规律性,所以随着后期的深入研究,通过改进传感器结构、加工工艺和装配方式,作者相信可以消除其测量误差中的规律成分,从而进一步提高该传感器的测量性能。