例谈高考圆锥曲线问题中的配极背景

张胜利

(新疆乌鲁木齐市第一中学 830000)

圆锥曲线是非常优美的曲线，高中数学中利用“坐标法”揭示了其丰富的性质，展现了完美的“数形结合”.其实，在研究直线与圆锥曲线的位置关系时，一些问题、结论已经涉及到圆、椭圆、双曲线、抛物线的极线；配极理论是圆锥曲线一套非常漂亮、实用的性质，在历年高考试题中也有它的背景.本文做些极线、极点的介绍、应用，与各位读者共同学习.

定义1圆锥曲线的配极：已知圆锥曲线Ω所在平面上一点P(非中心)，过P作两条直线PP1P2和PP3P4分别交Ω于两点P1、P2和P3、P4，过点P1、P2引Ω的切线交于点X，过点P3、P4引Ω的切线交于点Y，称直线XY是点P关于圆锥曲线Ω的极线，同时点P是直线XY关于圆锥曲线Ω的极点.我们把圆锥曲线的一对极点、极线称为配极.

显然，当点P在圆锥曲线Ω上时，极线就是过点P圆锥曲线Ω的切线；当点P在圆锥曲线Ω外时，极线就是过P引Ω的两条切线得两切点的连线.特殊的，圆锥曲线的焦点与准线就是一对配极.

一般的，设圆锥曲线Ω的割线PAB、PDC与Ω交于点A、B、C、D，AC与BD、AD与BC的交点分别为M、N，如图，则直线MN是点P的极线、直线MP是点N的极线、直线NP是点M的极线.

在直角坐标系中，有以下结论：

设圆(椭圆、双曲线)的方程为mx2+ny2=1，点P(x0，y0)是异于原点(中心)的点，则直线l：mx0x+ny0y=1就是点P的极线.

设抛物线的方程为y2=2px，点P(x0，y0)是异于原点(顶心)的点，则直线l：y0y=p(x0+x)就是点P的极线.

结合圆锥曲线的配极有以下结论：

一般地，过极点C的直线交极线于点D、交圆锥曲线于点A、B，则A、B、C、D是调和点列.

以上结论，可以查阅射影几何或其它相关书籍，这里限于篇幅就不证明了.下面主要探究几例高考试题中的配极背景.

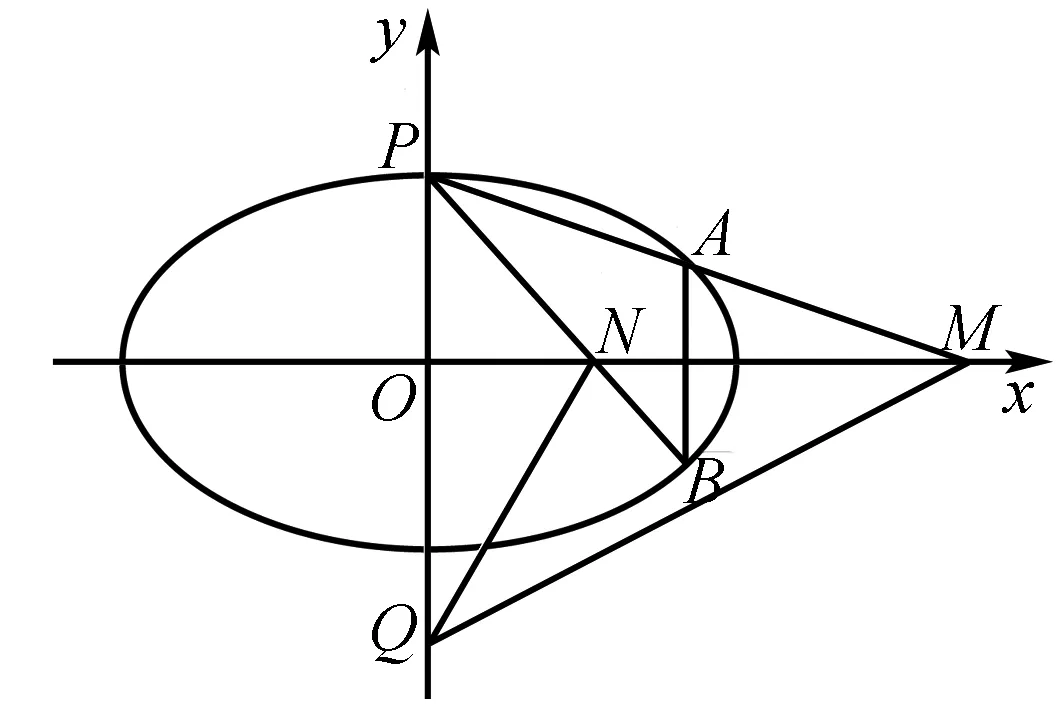
(1)求椭圆C的方程，并求点M的坐标(用m，n表示)；

(2)设O为原点，点B与点A关于x轴对称，直线PB交x轴于点N．问：y轴上是否存在点Q，使得∠OQM=∠ONQ？若存在，求点Q的坐标；若不存在，说明理由．

解(1)椭圆略.

通过分析配极，能够更进一步认识此问题的本质，求解也方便多了.同时，通过本例我们注意到了调和点列与定义等价的一个性质：已知A、B、C、D是调和点列，O是线段AB的中点，则OC·OD=OA2，反之也成立.

例2[2013·陕西卷(理)] 已知动圆过定点A(4,0)，且在y轴上截得的弦MN的长为8.

(1) 求动圆圆心的轨迹C的方程;

(2) 已知点B(-1,0), 设不垂直于x轴的直线l与轨迹C交于不同的两点P,Q, 若x轴是∠PBQ的角平分线, 证明直线l过定点.

解(1)略.

(2)由(1)知C:y2=8x，点T(1，0)关于C的极线方程是：4(x+1)=0即x=-1.

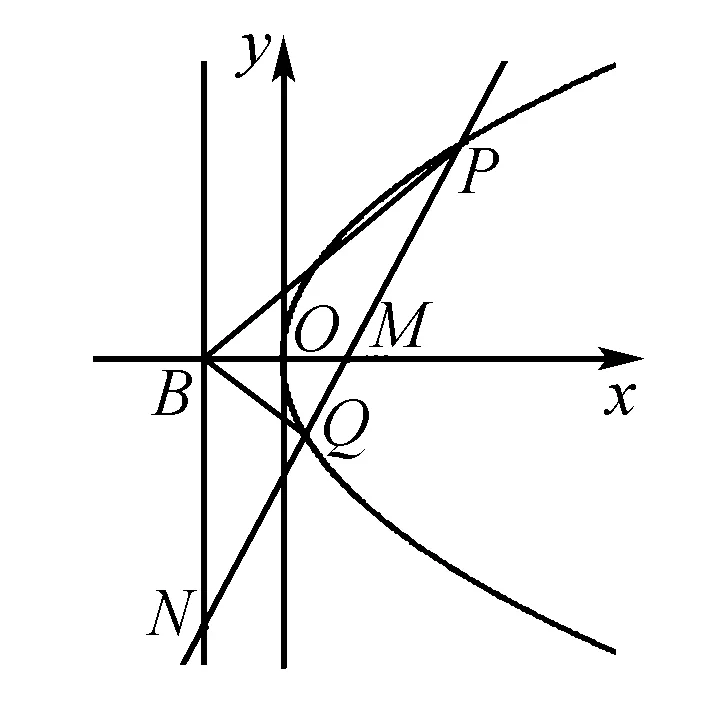
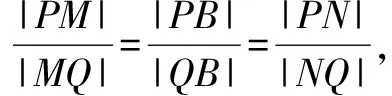
通过本例，我们发现：一条直线与一个角的两边及其内外角平分线的交点成调和点列.其实，这是调和线束的特殊情况.

定义3调和线束：如果共点的四条直线与一条直线的四个交点成调和点列，则称这四条直线是调和线束.

通过上面的例子我们可以得到以下结论：

如图，设l、m、n、k是调和线束(即A、B、C、D是调和点列)； 当OC是∠AOB的角平分线时，OD是∠AOB的外角平

分线，故OC⊥OD；反之，当OC⊥OD时，有OC平分∠AOB(证明略).

例3[2015·福建卷(文)]已知点F为抛物线E∶y2=2px(p>0)的焦点，点A(2，m)在抛物线E上，且|AF|=3.

(1)求抛物线E的方程；

(2)已知点G(-1，0)，延长AF交抛物线E于点B，证明：以点F为圆心且与直线GA相切的圆，必与直线GB相切.

解(1)略.

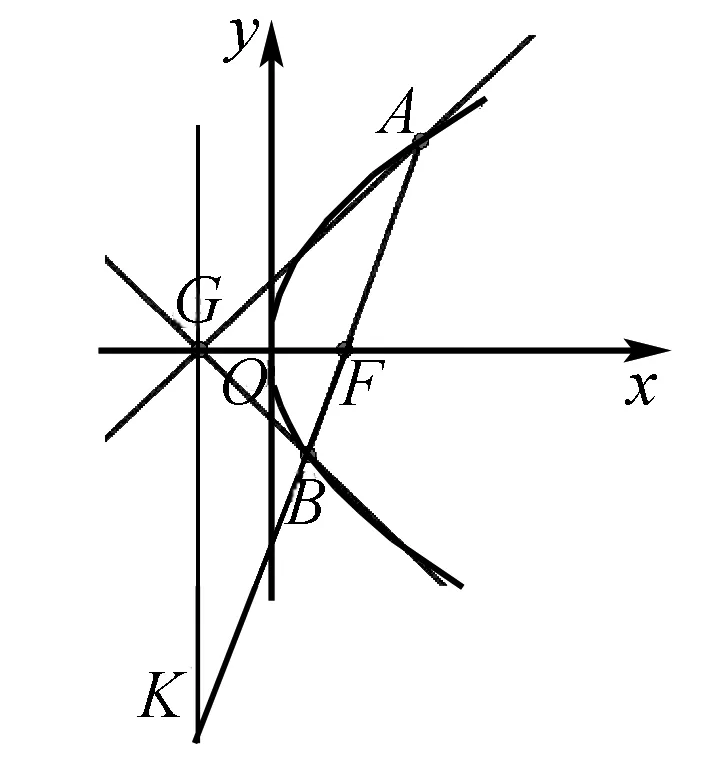
(2)由(1)知抛物线E∶y2=4x，焦点F(1，0)，准线x=-1，过点G作x轴垂线GK，如图，则直线GK是点F的极线.设直线AB交直线GK于点K，则A、B、F、K是调和点列，∴GA、GB、GF、GK是调和点列.而GF⊥GK，∴GF(即x轴)平分∠AGB，故以点F为圆心且与直线GA相切的圆，必与直线GB相切.

关于抛物线焦点弦、准线的综合问题经常见，本例揭示了其中一种的几何本质，让人印象深刻.

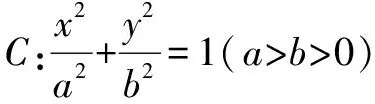
(1)求椭圆C的离心率；

解(1)略.

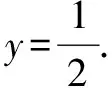
通过本例，我们知道了调和点列的又一个与定义等价的性质.根据调和点列的性质，可以证明：调和线束与任何直线相交所得的四个点都是调和点列.

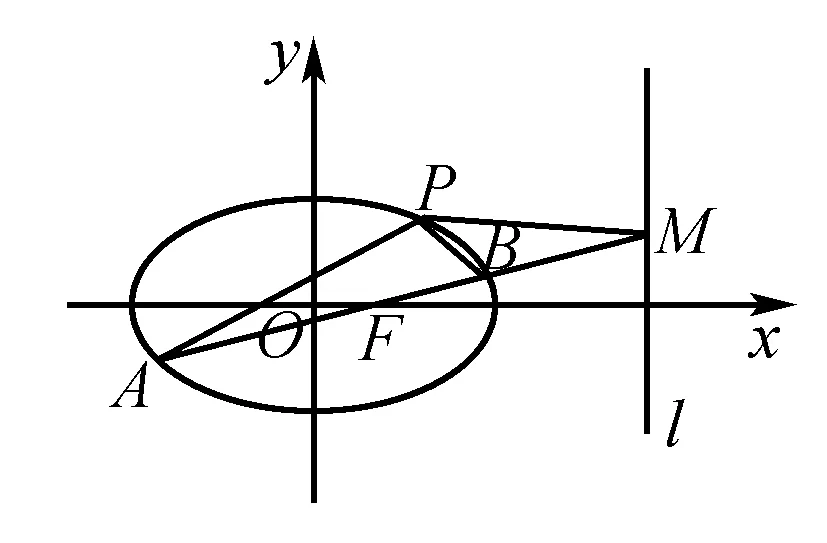
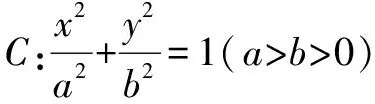
(1)求椭圆C的方程;

(2)AB是经过右焦点F的任一弦(不经过点P),设直线AB与直线l相交于点M,记PA,PB,PM的斜率分别为k1,k2,k3.问:是否存在常数λ,使得k1+k2=λk3?若存在求λ的值;若不存在,说明理由.

解(1)略.

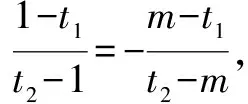
∴存在λ=2.

配极理论是射影变换在几何中完美地应用，是射影几何中的一个重要知识点.高中解析几何中一些结论都可以找到它的背景，引领一部分学生学习一点相关的知识，对于提升对几何的认识和数学素养都大有益处.笔者曾在奥赛辅导教学中有过尝试，一些学生很感兴趣，而且接受得比预想中的快，说不定就此在未来的数学家心中埋下了一颗种子，倘若如此，不失为基础数学教育工作者最大的欣慰！