异常值自识别的低秩矩阵补全方法*

李可欣，徐 彬，高克宁

东北大学 计算机科学与工程学院，沈阳 110000

1 引言

当矩阵的元素存在未知或缺失的情况下，可以采用矩阵补全方法根据已知元素估计未知元素，找到与原始矩阵尽可能相似的矩阵。目前矩阵补全已经应用到很多领域：机器学习[1]、视频去噪[2]、压缩感知[3]、图像处理[4]、无线传感[5]、目标追踪[6]等。Cai和Candès等提出奇异值阈值（singular value thresholding，SVT）算法[7]。利用奇异值分解（singular value decomposition，SVD）找到与原始矩阵尽可能相似的目标矩阵，但该算法每一步都进行SVD分解，这意味着每一步迭代都需要重新遍历所有样本，这样在处理大规模矩阵时需要巨大的计算时间和空间存储。为了解决大规模数据的矩阵补全问题，Wen等人在此基础上提出了低秩矩阵拟合算法（low-rank matrix fitting，LMaFit）[8]。LMaFit每一步迭代都只需解决一个最小二乘问题，因此计算速度和存储空间优于SVT算法。大量研究所知，目前LMaFit算法无法准确处理存在异常值的数据样本，且计算是一个迭代过程，每一步迭代都在上一步计算的结果基础上进行，如果计算包含异常值的样本，将会导致不准确的结果，因此在数据处理之前识别并处理异常值将会提高算法的准确率。

为了解决上述问题，本文提出了一种新的非线性过放缩异常值自识别算法。该方法可以识别出异常值的位置并对异常值进行近似值替代，降低异常值对结果的影响，相较于已有矩阵补全算法的恢复结果也更加精确。

2 相关工作

陈蕾等人详细地介绍了矩阵补全模型及相关算法应用研究[9]，在矩阵补全的相关算法中，大部分算法可以处理添加高斯噪声的数据，却对真实数据中的异常值无法进行有效的处理[10]，而现实生活中很多情况例如电影、书籍、游戏等的分类问题都是存在异常值的样本问题。在这样的情况下，如何降低异常值对最终结果的影响是提高矩阵补全算法鲁棒性的重点。在之前的工作中[11]，在本校的在线平台增加学生互评系统，学生之间互相评价分数反映该学生的学习情况，并利用学生平时成绩衡量学生互评成绩的可信度。但是在实际情况中，由于现实情况的不可控性，学生的成绩存在缺失或存在异常点，例如学生成绩超出成绩区间、波动较大的异常数据等情况。当剔除不合理的成绩数据后，形成了存在较多缺失值的成绩矩阵。使用矩阵补全方法可以对成绩数据补全，可以使数据完整，但对于存在异常值的学生成绩使用矩阵补全算法，不仅与实际情况有所偏差，更有可能与真实情况背离。因此降低异常值对矩阵补全结果的影响是目前存在的重点及难点。

为了解决因异常值而导致的分析结果存在偏差问题，相关学者提出了许多有效的算法，例如Ji等人提出黎曼信赖补全方法（Riemannian trust-region method for low-rank matrix completion，RTRMC）[13]。利用低秩的几何约束在格拉斯曼流形上重塑无约束优化问题；Boumal等人采用非奇异值分解SVT算法[7,12]，在SVT的基础上提出通过直接对矩阵进行牛顿迭代。由于SVT模型每一次迭代都要在全部样本上进行SVD分解，虽然理论上可行，但是在处理大规模数据情况下的效果却并不尽人意。Jain等人通过奇异值映射保证秩最小化方法[14]，提出一个简单且快速的奇异值投影算法（singular value projection，SVP）映射约束来达到最小化秩的目的，从而解决限制等距约束问题。Dong等人利用最少数据恢复矩阵的算法（special matrix completion，SMC）[15-16]，但是在实验中可以看到在矩阵数目为500左右时达到最优，对于过少或过多的数目的矩阵处理较乏力。

为了解决上述问题并降低异常值对于矩阵补全结果的不利影响，提高算法的精确度，本文在低秩矩阵拟合算法的基础上提出一种新的异常值自识别算法（self-identifition of outliers for low-rank matrix completion，SIOMC）。与传统算法不同的是，该算法选择直接优化原始矩阵中的未知元素使原始矩阵趋于低秩结构，在此基础上进行矩阵补全，通过构造误差矩阵，识别矩阵中的异常值，降低异常值对算法鲁棒性的影响。误差矩阵在每一步的迭代中都会更新，该矩阵显示上一步的误差结果，并返回异常值的位置，使用近似值对异常值进行替换，增加算法的精确度。

本文分别进行了人工数据和真实数据的矩阵补全实验分析，讨论四种矩阵补全算法的时间及鲁棒性能。实验结果显示SIOMC算法相较于其他矩阵补全算法，在处理异常值矩阵性能更加优秀。其他方法包括奇异值阈值方法（SVT）、快速SVT方法、不精确增广拉格朗日方法（inexact augmented Lagrange multiplier，IALM）和低秩矩阵拟合方法（LMaFit）[17-20]。

3 算法描述

在算法的描述之前，先给出一些基本的定义:

令X=(x1,x2,…,xn)为大小为m×n的矩阵，本文定义{1,2,…,m}×{1,2,…,n}是观察到的X中的元素的位置集合，而ΩC为缺失元素的位置集合。定义PΩ为矩阵X在集合Ω上的正交投影算子：

低秩近似算法目前可以分为两方面：最小化核范数和矩阵分解。绝大多数的矩阵补全问题都是在如下模型的基础上提出的：

式中，X为M在Ω上的投影矩阵，大小是m×n，Ω为相应指示集，表示在Ω区域内进行矩阵补全算法的研究，rank(X)代表矩阵X的秩。明显可以看出上述的问题是一个NP难问题，因此上述问题可以转化为最核范数问题：

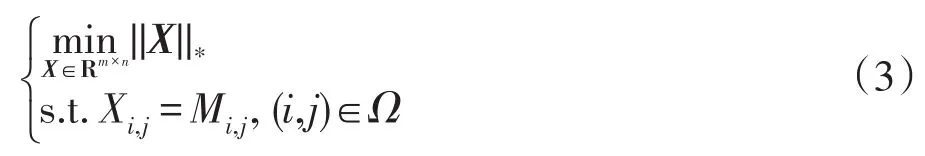
其中，M为原始矩阵，秩为r,UVT是目标矩阵，U和V分别是n1×r和n2×r的矩阵，由于上式是非凸的，考虑其拉格朗日形式：

优化过程分别在U、V和X上最小化，得到最后的最优值。

4 优化算法

为了降低异常值对算法鲁棒性的影响，本文提出SIOMC方法提高算法的精确度，SIOMC模型如下：

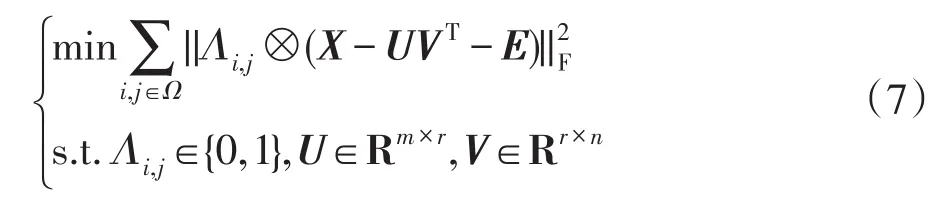
式中，X是原始矩阵，引入异常值检测结果矩阵E，UVT是想要得到的目标矩阵，⊗表示分量相乘。E为上一步迭代产生的误差稀疏矩阵，其中Ei,j=-ÛV̂T。如果Ei,j≠0 ，表明对应的Xi,j可能为异常值。在接下来的步骤中，将对异常值进行处理，具体处理过程会在后续表明。其中Λi,j代表迭代中对Xi,j的控制参数，每一步的迭代过程中，在更新的U、V的基础上识别异常值的位置。

本文采用最小二乘法优化上述问题，首先设置误差矩阵E初始值为0，采用重复迭代方法固定U和V更新E和Λ，然后固定E和Λ更新U和V。

首先固定U和V，求解如下问题：

上述过程中，E为误差矩阵，Λi,j识别异常值并记录异常值的位置。如果Xi,j不是异常值，那么直接将Xi,j投影到Ω上，否则将其值置为0。

在算法的每一次迭代过程中，通过以下操作得到误差矩阵：

引入误差阈值γ=UVTij-Xij，其合理性的详细证明可参考文献[22]，在误差矩阵超过定义的阈值范围的情况下，判断Xi,j为异常值，下一步将进行：

如果该值为异常值即Λi,j=1，将其与进行替换，上一步迭代中更新的目标矩阵中对应的值。

接下来继续固定误差矩阵E和Λi,j，更新U和V，解决如下问题：

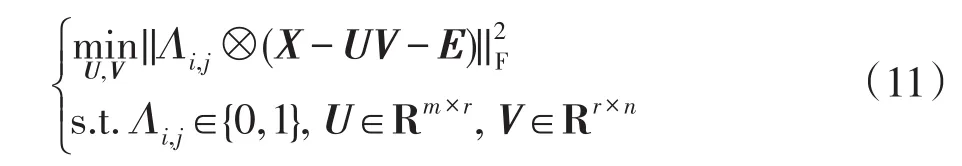
更新U：

更新V：

上述过程可以定位异常值位置并自动将近似值与异常值替换，每一步都更新了数据，提高了算法处理结果的精确度，从而保证最终结果的准确性。SIOMC算法详细描述如算法1所示。

算法1 SIOMC

Input:MatrixX,Ω,PΩ(M),r＞0,maxiter.

Initialize:Λij=1for(i,j)∈Ωand otherwise=Ω,iter.

Whileiter＜maxiterdo

5 实验

在本章实验部分，基于人工数据集和真实数据集比较SIOMC算法和LMaFit算法在矩阵补全问题上的效果。本校学生在线成绩比较SVT、IALM、LMaFit和SIOMC算法，使用RMSE（root mean square error）和Relative error分别衡量算法的准确性。在本文实验中，程序均用Matlab2016编程，在双核i7-4770处理器、内存为16 GB的台式电脑（操作系统为Windows 7）上运行。

5.1 合成数据实验

首先构造两个矩阵ML∈Rm×r和MR∈Rr×n，每一个元素都根据独立同分布高斯采样，生成秩为r的矩阵M，M=MLMR。令MΩ是矩阵M中可观察得到的部分，位置集合Ω是通过随机采样得到的。令p是观察得到的元素数量和矩阵M中所有m×n个元素的比例。均方根误差和相对重构误差经常被用于衡量本文所述类似算法的准确性，因此实验采用均方根误差和相对重构误差指标来衡量不同算法所处理矩阵的准确性。

均方根误差的定义为：

这里的num是测试样本数目。

相对重构误差的定义为：

Fig.1 RMSE versus different ranks图1 随着秩变化RMSE的变化情况

在实验中，设置m=n=1 500，p=0.8，c=0.05，λ=0.5，分别调节r的大小，r的取值范围为{5,10,15,20,25}，实验结果取10次实验的平均值保证实验的公平有效，对比不同秩大小的实验的结果如图1所示。同时为了探究噪声的比例对算法性能的影响，验证SIOMC相较于其他算法在异常值问题上具有更优秀的鲁棒性，在原始数据基础上增加不同比例的噪声（noise level）来观察不同算法对数据处理的情况。实验中保持矩阵的秩为5不变，逐步改变noise level取值范围为{0.25,0.30,0.35,0.40,0.45,0.50}，noise level代表噪声数据在实验数据中的比例，通过观察noise level变化过程，算法RMSE变化的趋势如图2所示。

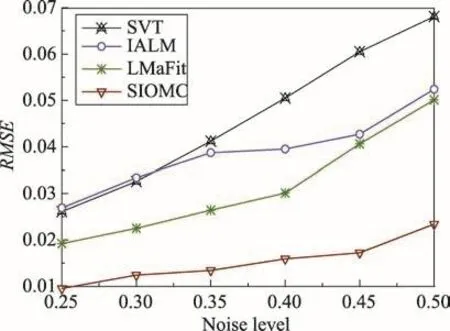
Fig.2 RMSE versus noise level图2 随着噪声变化RMSE变化情况

图1为随着秩变化SIOMC算法和SVT、IALM和LMaFit三种算法的RMSE值的曲线图。从图中可以看出，随着矩阵秩增加，算法的RMSE呈下降趋势。从图1显示，在矩阵秩从5递增到25的过程中，代表SIOMC算法的曲线数值上结果优于其他三种算法；图2为随着噪声变化四种矩阵补全算法RMSE的变化曲线图。从图中可以看出，随着noise level增加，SIOMC算法的曲线相较于其他算法曲线趋势更加平缓，说明SIOMC可以更好地处理异常值情况，具有更好的鲁棒性。因此可以总结为SIOMC算法在模拟数据的处理上相较于LMaFit等其他三种算法无论在增加矩阵的秩和噪声比例的情况下，因为SIOMC在每一步迭代都对异常值进行处理，上一步的异常值没有对下一步数据计算产生影响，因此有较强的鲁棒性。

5.2 真实数据实验

在本节中，将提出的算法SIOMC应用到具体的推荐系统问题中，分别基于公开数据集和本校在线平台成绩数据进行算法比较。公开数据集为广泛应用的推荐系统数据Jester数据集（http://www.ieor.berkeley.edu/～goldberg/jester-data/）和 Movie 数 据 集（https://grouplens.org/datasets/movielens/）。Jester数据集有73 496个用户对100个笑话开展的410万次评分，不同的数据集代表不同大小的数据规模；Movie数据集中是用户对自己看过电影的评分，三个数据集不同规模，用来比较实验中算法应用于不同大小数据规模的实验性能，数据集详情如表1所示。第一部分实验选用的两个数据集是人为对笑话或电影进行评分，整个评分矩阵是高度稀疏的，不能保证所有的评分都在正常范围内。例如在对电影的评分中，有的人可能对没看过的电影进行评分，因此数据集中存在部分异常值的情况。

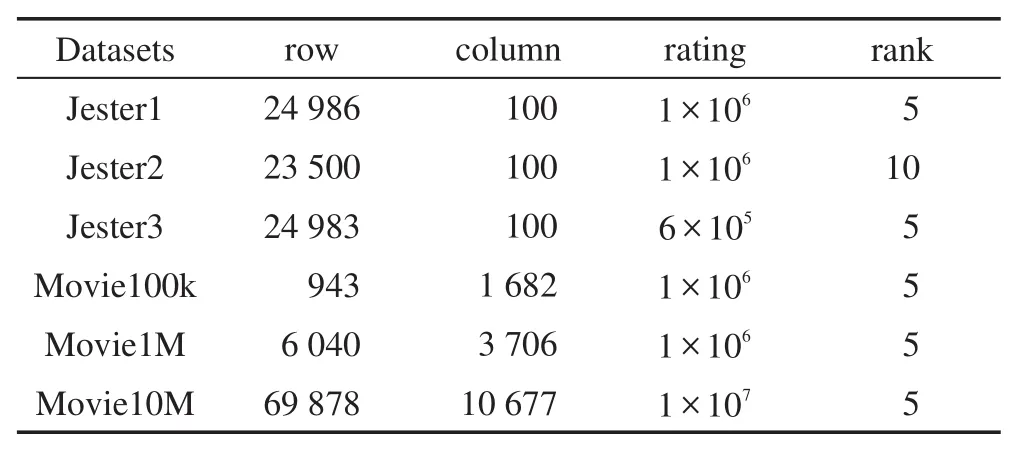
Table 1 Details of real datasets表1 真实数据集细节

实验中将这些数据分为训练集和测试集两部分（采样率为0.8），随机选取80%评分信息作为训练集，其余部分作为测试集。实验中采用式（15）给定的error作为矩阵恢复准确性的度量。分别将SIOMC算法与其他三种矩阵补全算法相比较，性能比较详情如表2所示。

Table 2 RMSE results of different algorithms on different datasets表2 不同数据集算法RMSE比较

表2显示进行SIOMC处理后的数据error的值相较于SVT、IALM和LMaFit更小。SIOMC在过程中增加异常值处理机制，识别异常值的同时对异常值进行近似值代替处理，能够降低异常值对结果的不利影响，提高算法的鲁棒性，从而使结果更加精确。

基于MovieLen三个数据集分别采用四种矩阵补全算法对数据进行处理，并记录运行时间，如表3所示。采样率分别为0.3、0.5、0.8。

表3显示，随着训练集规模的增加，四种算法的运行时间都相应增加，其中SVT的增加速率在四种算法中最快，LMaFit与SIOMC的速率相似。以上四种矩阵补全算法，LMaFit的运行时间比其他三种算法同等采样率情况下小，由于本文提出的算法增加了异常值矩阵，但由于异常矩阵仅记录补全过程中的差异，因此运行时间虽不及LMaFit，但也优于SVT算法和IALM算法。

第二部分实验选择在线平台开放课程的学习者成绩，由于测试题不是强制完成项目，许多学习者只完成了部分测试题，造成数据中存在大量的缺失项。之前的工作为根据学生在线成绩的互评分数构建学生成绩互评系统，在验证学生互评成绩的可信度的过程中需要根据学生之前的在线成绩判断学生互评成绩的可信度，学生的在线成绩的完整性和准确性需要得到保证，因此在之前的工作中尝试利用矩阵补全技术对缺失数据进行补全，取得良好的补全效果。为了验证SIOMC算法能否更好地应用于在线平台学习者成绩数据，降低成绩数据中异常值对结果的影响，将SIOMC算法应用于本校在线平台一个学期内的两门课程测试成绩上，同时与其他矩阵补全算法比较性能。两门课程的基本信息如表4所示。

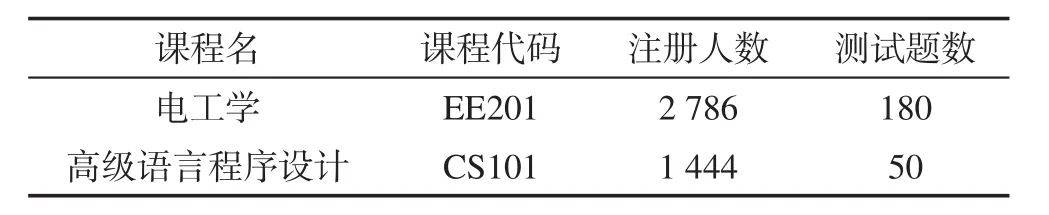
Table 4 Courses information表4 课程基本信息

图3为成绩矩阵最大的特征值大小分布情况，从图中可以看出，学生成绩矩阵的信息主要分布在部分数值较大的异常值上，因此利用矩阵补全算法来恢复学生成绩中缺失信息是非常合理的。

Fig.3 Grade matrix singular value distribution图3 学生成绩矩阵奇异值分布情况

Table 3 Running time of different algorithms on different datasets表3 不同数据集算法运行时间比较

基于在线平台学习者课程成绩数据进行矩阵补全算法的相关实验，分别比较SIOMC与SVT、IALM和LMaFit三种矩阵补全算法的性能。本实验中分别采用RMSE和error衡量算法性能，实验结果包括的RMSE和error详细信息分别如表5、表6显示。表5显示不同算法在课程成绩数据上的RMSE对比，表6显示不同算法在课程成绩数据上的error指标对比。

Table 5 Comparative RMSE measurement on course data of different algorithms表5 不同算法在课程成绩数据上的RMSE指标对比

Table 6 Comparative error measurement on course data of different algorithms表6 不同算法在课程成绩数据上的error指标对比

从表5和表6可以看出，比较SVT、LMaFit、IALM和SIOMC对本校学生在线成绩的衡量结果显示，SIOMC相较于其他三种算法具有更高的精确度，在处理真实数据的情况中，SIOMC算法可以较为精确地处理数据。

6 结论

本文提出了一个新的能够准确处理低秩矩阵的方法，不同于其他算法直接优化整个矩阵，本文算法在优化之前对异常值进行识别并处理。该过程可以将异常值自动处理，从而提高后续迭代过程的精确度。通过准确识别异常值的位置并对异常值进行处理，从而使结果更加精确。通过每一步迭代产生的误差矩阵返回的异常值位置可以快速准确地识别异常值并对其进行处理。实验证明，这个方法与LMaFit相比在增加噪声的情况下有更好的鲁棒性，并且结果更加精确。