分层递进的改进聚类蚁群算法解决TSP问题*
冯志雨,游晓明,刘 升
1.上海工程技术大学 电子电气工程学院,上海 201620
2.上海工程技术大学 管理学院,上海 201620
1 引言
旅行商问题(traveling salesman problem,TSP)属于NP难问题[1],仿生进化思想的发展为NP难问题提供了新的思路,这其中以蚁群算法(ant colony optimization,ACO)最为显著。蚁群算法的提出[2],是源于Marco Dorigo的博士论文,它是一种具有进化思想的启发式算法,根据正反馈机制实现种群间的信息交流。蚁群算法1992年提出至今,针对算法的不足,研究学者一直进行着改进工作以提高算法的实现效率。Dorigo等人[3]和Stützle等人[4]分别提出了蚁群系统、最大-最小蚁群算法,对传统蚁群算法在信息素更新方式以及界限进行了改进;对于TSP问题,有n个节点,那么相应的就会有(n-1)!个可行解,对应的时间复杂度就变成了O(n!)。随着TSP问题规模越来越大,时间复杂度会愈加增大,运算难度就会愈加增大。传统蚁群算法在解决大规模的TSP问题时,运算时间会增大并且解精度会降低。因此,应对TSP问题,越来越多的学者试着结合多种智能算法的优点去获得更好的运算性能。文献[5]提出蚁群算法(ACO)与3Opt并行合作混合方法。利用蚁群算法找到TSP问题的路径解,然后运用3Opt算法优化找到的路径解,进一步提高解精度,避免算法陷入局部最优。虽然算法运行时间有所提高,但是为了算法中种群的并行运行,需要不止一台实验的仿真设备来完成,这无形中增大了仿真硬件要求。文献[6]提出粒子群算法(particle swarm optimization,PSO)+蚁群算法(ACO)+3Opt方法,解决不同的TSP问题所需要的参数不尽相同,故利用粒子群算法去优化蚁群算法中的信息素因子α和启发式因子β,以便蚁群算法可以找到期望的路径最优解。然后再经3Opt算法优化解路径。虽然算法提高了某些TSP问题的解精度,但是并没有缩短算法的运算时间,并且当TSP问题规模增大的时候,提出的改进算法并没有获得较好的解路径值。文献[7]提出融合遗传算法、模拟退火、蚁群算法、粒子群算法等多种群技术去解决TSP问题。先通过蚁群算法获得初始最优路径解,然后通过遗传模拟退火算法去优化初始最优路径,当迭代完成一段时间后,通过粒子群算法去优化各路径上的信息素,然后再进行迭代运行。该算法在较大规模的TSP问题上获得了理想的解路径值,但是由于融合了多种优化算法,算法本身的计算复杂度被提高了,运算时间没有缩短。文献[8]提出了基于蚁群算法的改进信息素更新机制以及新的信息素平滑机制去解决TSP问题,利用迭代最优路径上的信息素确定新探边的动态最佳路径变化信息,从而加快算法收敛速度,利用平滑机制对信息素矩阵进行重新初始化,从而扩大种群多样性,增强算法的全局搜索能力,但是算法的计算复杂度为O(n2),并没有较大程度地降低算法的计算复杂度。
本文提出的DP-ACS(density peak clustering algorithm-ant colony system)算法利用分工合作[9]的思想,将大规模的TSP案例进行节点分组归纳,然后运用改进的蚁群算法寻找新形成的二类TSP问题的解路径,最终切割断点重组二类TSP问题的解路径构成原始TSP问题的最优路径。DP-ACS算法在保证问题解精度的前提下,明显加快了算法运算时间,并且有效降低了算法的时间复杂度。
2 相关工作
2.1 TSP问题描述
旅行商问题是一个经典的组合优化问题,组合优化是根据数学方法对某离散事件进行整编、分组、排序等。旅行商问题是说一个旅行者要走遍给定数量的城市,但是前提这些给定的城市只允许旅行者拜访一次,要求找出旅行者走遍每个城市后的最短路径。给定的城市数量越大,求解问题的空间复杂度、时间复杂度不可避免地会增大,而且呈指数函数增长,因此TSP问题的解不是穷举就可以得到的,问题的复杂度已经远远超出了人们想象。求解TSP问题的算法一般分为两大类:精确算法和启发式算法。前者适用于小规模旅行商问题,后者适用于中大型TSP问题。精确算法主要有定界法、规划法等。启发式算法有GA(genetic algorithm)、SA(simulated annealing)、PSO、ACO等。其中蚁群算法,由于具备进化思想,为解决旅行商问题提供了新的思路。
2.2 蚁群算法求解TSP问题
在标准的蚁群算法中,蚂蚁根据式(1)[3]状态转移概率规则,判断蚂蚁下一个去往的城市。

式中,τij(t)是t迭代过程中,城市i与j连接路径上的信息素值;ηij是城市i与j连接路径长度的倒数值,是一种启发式信息,如果城市i与j连接路径长度越短,那么蚂蚁选择的下一个城市越可能是j;Allowedk表示蚂蚁k未走过的城市;α和β分别决定了信息素和启发因子的重要性。当所有蚂蚁完成了一次完整的路径构建,即完成一次迭代,此时信息素的更新将会按照式(2)进行。

式中,ρ表示信息素挥发参数,m是每次迭代的蚂蚁总数量,表示蚂蚁k在路径(i,j)上释放的信息素值,Lk(t)是蚂蚁k旅行路径长度。通过设置最大迭代次数,当算法运行迭代数达到设定最大值,结束运行,得出算法最优解。如果在迭代过程中出现停滞现象,则初始化处理,从而摆脱停滞,继续迭代运行,直到达到设定的迭代上界。
2.3 密度峰聚类算法
密度峰聚类算法(density peak clustering algorithm,DPCA)[10]的基本思想是对于一个数据集,聚类中心被一些低局部密度的数据点包围,而且这些低局部密度的点距离其他有高局部密度的点的距离都比较大。DPCA主要有两个需要计算的量:(1)局部密度ρi;(2)与高密度点之间的距离δi。密度峰聚类算法是将给出的数据点通过计算点与点之间的欧式距离dij,然后根据ρi以及δi选取出聚类中心,聚类中心的选取衡量标准是具备较大局部密度ρi和较大距离δi。然后将所有非聚类中心的散点归类到比自身密度更大的最相近的类中心所在的簇中。
2.3.1 局部密度ρi

其中,dc是截断距离,N是数据点总数,percent是比例因子,本文设为2%,ρi是统计数据点i与其他数据点的欧式距离小于dc的个数。
2.3.2 与高密度点之间的距离δi

式中,δi是在所有较数据点i的局部密度ρi都大的数据点中,选出那些点与数据点i的欧式距离的最小值。
2.4 3Opt算法
3Opt[11]是一个应用于优化旅行商问题解质量的局部搜索算法。在本算法中,3Opt主要用于从蚂蚁找到全局最优解中任意挑选3对节点,打乱重新组合3对节点的连接,并记录所有重新组合的8种连接情况。然后评估重新连接的线路质量与最初线路质量的好与差,如果比对出更好的连接线路,则覆盖之前蚂蚁找到的全局最优线路,反之保留起初线路。如果蚁群算法没有使用3Opt,蚂蚁容易陷入局部最小并导致搜寻不到最好的旅行长度,故3Opt进一步遏制了局部最优情况的发生。如图1所示,左侧连接图有3条边经3Opt算法处理后可以重新生成更优的连接图。

Fig.1 3Opt algorithm implementation图1 3Opt算法实现
2.5 粒子群算法
粒子群算法[12]是一种基于社会环境的自适应算法,其中设置一组种群粒子去访问给定域的尽可能的位置,每个位置都有对应的可计算的适应值。在每次迭代中,粒子将随机地返回到先前的最佳适应位置和种群最佳适应位置。种群中的所有粒子都在分享自身找到的最佳搜索区域的信息。
粒子的运动由式(5)主导,vf表示粒子f的速度,xf表示粒子f的位置。
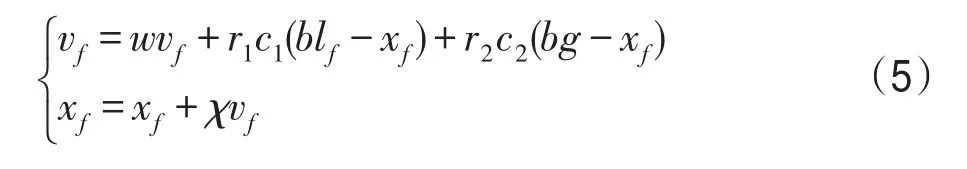
式中,c1、c2是非负整数,分别称作“认知”与“社会”,前者是粒子本身的思考,后者是粒子间的信息共享与合作,都是学习因子。r1、r2是[0,1]内的随机数,都是比例因子。w、χ是非负实数,分别称作惯性权重和收缩因子。blf表示粒子f经过的历史最好位置,bg表示种群中所有粒子所经过的最好位置。
3 改进算法(DP-ACS)
运用蚁群算法求解TSP问题的过程中,随着TSP问题规模的增大,蚁群算法的运算复杂度会呈指数上升。当TSP问题中的节点数超过100时,依靠蚁群算法自身很难在运行时间和解精度之间找到平衡性,往往会消耗更多的时间去寻求更高的解精度。文献[13]提出当TSP问题中的城市节点小于40个时,蚁群算法在运行时间以及求解的精度都获得最优。文献[14]提出了K-means聚类算法,这种算法快速、简单,但是局限于处理数据分布呈球状的簇。密度峰聚类算法是一种基于密度的聚类算法,寻求被低密度区域分离的高密度区域,能克服基于距离的算法只能发现“类圆形”的聚类的缺点,聚类形状不受限制。
3.1 改进的密度峰聚类算法
密度峰聚类算法选取聚类中心依靠局部密度ρi和与高密度点之间的距离δi,故定义式(6)中γi为衡量点i是否为聚类中心:

因为聚类中心同时具备较大的ρi和δi,所以γi的值越大,说明点i越有可能是聚类中心,对集合γ进行降序排序,选取集合γ的前8%个点,记为DE(density),对排序后的点重新编号,记为j,然后绘制γ关于j的数据图,数据图呈非递增状态。
定义ε为拐点,点ε为数据图中前后两点的γ值相差过大的点,点ε满足式(7)给出的条件:

式中,kj表示点j+1与点j构成线段的斜率,当确定拐点之后,由于集合γ是降序排序的,故潜在的聚类中心点均位于拐点的左侧。当确定了潜在聚类中心后,按照需要解决的TSP问题规模确定划分多少个聚类中心。
如图2,以TSP案例lin105为例,利用Matlab仿真绘制出γ关于j的排序图,其中横轴对应的是筛选出的城市节点重新编号,纵轴对应的是原城市节点根据式(6)计算的γ值,图中数据点旁的标号是原TSP问题的城市编号。从图2可以得出城市节点51是拐点,故城市节点77、23均为潜在的聚类中心。
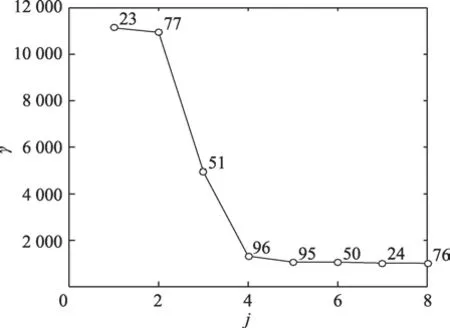
Fig.2 γsorting chart图2 γ排序图
3.2 改进的蚁群算法
文献[2-4]的局部信息素更新都是根据式(8)进行的。

式中,ρ表示信息素挥发参数,取值范围在[0,1]。一般将ρ的值设为0.1,但是TSP问题不同的数据规模算法需要的运算复杂度是不同的。ρ设为定值将不能满足问题的解要求,比如kroA200,需要将ρ的值设大一些,以防蚁群算法过早收敛,获得局部最优解,降低了算法精度。因此提出式(9)自适应地改变信息素挥发值。

其中,k为比例因子,设为0.1;c为归一化因子,设为2。通过式(9)将信息素挥发参数ρ与信息素τij(t)之间建立线性关系。以e为底的指数函数呈单调递增的特性,而信息素τij(t)的值随着算法迭代运行呈上升趋势。对τij(t)取反处理,这样经exp函数处理后所得值控制在(0,1)内,从而经式(9)处理,信息素挥发参数ρ随着信息素τij(t)的增大而增大,并且ρ的值控制在(0.1,0.2)。
算法迭代运行初期,TSP问题中节点构成的路径上面蚂蚁数随机,信息素相差甚微,路径与路径间的受蚂蚁的欢迎度相差不大。随着算法的迭代运行推进,路径上面的信息素量的差距开始拉大,此时某些受欢迎度高的路径上的信息素值较高,这时在还没有找到全局最优路径的情况下,蚁群算法很容易陷入局部最优。这时根据式(9)的关系,避免了信息素过高带来的影响,此时信息素挥发参数对应提高,有效遏制了较欢迎路径上的信息素浓度的进一步提高。反过来,当信息素挥发参数ρ值升高时,必然会造成算法收敛速度的下降。这时候根据式(9)的关系,信息素τij(t)必然会略有提高来应对信息素挥发参数ρ值升高带来路径上面的信息素残余量过少的情况,在一定程度上避免了蚁群算法收敛速度减缓的情况发生。信息素挥发参数ρ与信息素τij(t)之间相互平衡,当ρ过大时,τij(t)相应就会增大,避免算法运算复杂度的上升;当τij(t)过大时,ρ相应就会增大,避免算法过早收敛陷入局部最优。
3.3 改进算法的流程图
本文DP-ACS算法求解旅行商问题的基本步骤如图3所示。
由图3可以看出,本文提出的改进算法(DPACS)先进行设置初始参数值,例如最大迭代次数、城市节点上信息素初始值、信息素挥发参数的初始值、蚂蚁数量等,然后根据初始TSP问题数据集给定的节点坐标,运算节点与节点之间的欧式距离,进而根据式(3)截断距离的定义计算dc,再根据式(3)、式(4)计算出每个节点的局部密度ρi以及与高密度点之间的距离δi。通过改进的密度峰聚类算法确定拐点,根据拐点的位置筛选出潜在的聚类中心,聚类中心的个数由初始TSP问题规模决定。根据选举出的聚类中心形成簇,每个簇包含一个聚类中心,一个城市节点只能属于一个簇。由于每个簇包含的节点数不尽相同,故利用粒子群算法去寻找对应不同规模的TSP问题应该设定的蚁群算法的信息素因子α和启发式因子β。形成的这些簇中的数据节点各自又构成了新的TSP问题,本文称为二类TSP问题。用具备自适应局部信息素更新的蚁群算法对二类TSP问题求解最优路径解,当这些二类TSP问题结束运行后,通过近邻原则选取两个相邻簇之间最近的两个节点,切割断开经过这两个节点的相关路径,通过之前断开的节点之间的相互连接实现两簇相连的效果,依此类推,将所有形成的二类TSP问题解路径重新组合成全局解路径,这样二类TSP问题将还原成初始设置的TSP问题,解路径从区域连接重新融合组成整体。再将重新连接后的全局路径经过局部优化策略3Opt的处理,以达到进一步优化重新连接后的全局路径的效果。最后通过算法辨别是否达到了预先设置的迭代次数上限。如果达到了,算法退出运行,输出运行结果;否则,算法继续迭代运行。如果算法在运行过程中出现停滞状况,算法将进行初始化信息素操作,以达到强制算法恢复运行的效果。
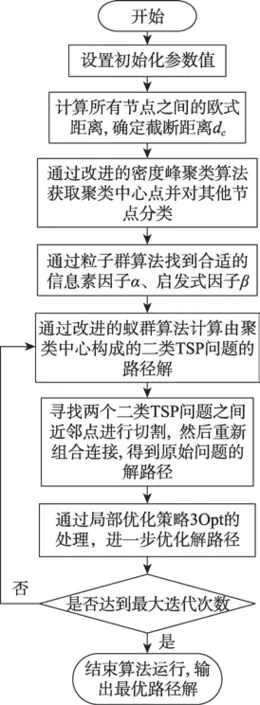
Fig.3 DP-ACS algorithm flowchart图3 DP-ACS算法流程图
3.4 DP-ACS算法的原理图
如图4,以TSP问题lin105为例,改进算法先经过密度峰聚类算法处理,选取出3个聚类中心,分别是初始TSP问题的节点23、51、77,然后对新形成的二类TSP问题经改进的蚁群算法运算,找出各自的最优路径解。由图4可知新形成的二类TSP问题构造的是密闭的环形路径解,需要通过近邻原则选取节点进行分割。将左侧的二类TSP问题的节点39与节点37之间的线段切割断开,将右侧的二类TSP问题的节点2与节点9之间的线段切割断开,然后将左侧的二类TSP问题的节点69与右侧的二类TSP问题的节点1相连。因为TSP问题中规定每个被访问的城市节点只允许访问一次,考虑到构建的全局最优路径解最短的要求,所以断开右侧的二类TSP问题的节点1与节点4之间连接的线段,然后将节点4与节点2相连。依此类推,断开中间的二类TSP问题的节点2与节点18、节点3与节点4、节点19与节点22之间的线段,将左侧的二类TSP问题中的节点37与中间的二类TSP问题的节点3相连,将右侧的二类TSP问题的节点9与中间的二类TSP问题的节点22相连。同样考虑到每个被访问的节点仅允许访问一次,将中间的二类TSP问题的节点2与节点4相连。最终经过改进的蚁群算法运算的所有二类TSP问题的局部最优路径重组构成了初始TSP问题的全局最优路径解,再经过3-Opt算法优化解路径,最后得到了lin105问题的最优路径解,即14 379。

Fig.4 DP-ACS algorithm schematic图4 DP-ACS算法原理图
4 仿真实验与结果分析
本文算法采用Matlab 2014b仿真软件,基于Intel®CoreTMi5-4200M CPU@2.50 GHz处理器,RAM为16 GB,操作系统为64位的Win10。本文选取了TSPLIB里的典型问题集,这些问题集通常用于测试和优化算法。本文将问题集分为两组进行实验,一组是小规模,另一组是大规模。参考文献[15]可知,密度峰聚类算法处理后的TSP问题形成的二类TSP问题规模在30~40个数据集节点最优。
如表1,利用粒子群算法中的粒子与种群寻找对应不同问题集的蚁群算法的信息素因子α和启发式因子β。

Table 1 Sets of parameters factor values表1 参数因子值集
如表2,设置蚁群算法的初始参数值以及算法运行迭代门限值等。

Table 2 Setting of basic parameters表2 基本参数设置
表2中ρ表示信息素挥发参数,Nmax表示算法运行迭代门限,Q表示蚂蚁循环一周释放的信息素总量,m表示蚂蚁数,n表示城市节点数,τ0表示信息素初始参数值。
4.1 DP-ACS算法处理小规模TSP问题
图5给出的是蚁群算法在迭代运行10次时,添加密度峰聚类算法和不添加密度峰聚类算法进行实验比较。

Fig.5 Comparison of algorithm running time图5 算法运行时间对比
从图5可以得出,经过密度峰聚类算法处理分割的TSP问题虽然在蚁群算法运算过程中还是需要一些时间,但是问题规模数据集节点的减少,降低了蚁群算法运算时间,并且运算时间减少会随着问题规模的增大而越发明显。当TSP案例的城市规模小于100时,算法之间的运行时间差距并不明显,随着城市规模增大,运用密度峰聚类算法所显现出的优势越发明显。以kroA100问题为例,算法运行时间开始加快,比不使用密度峰聚类算法降低了1.59 s。以ch150问题为例,算法运行时间明显加快,比不使用密度峰聚类算法降低了4.70 s。
如表3所示,选取6个规模不同的TSP问题案例,分别添加3Opt算法和不添加3Opt算法进行20次仿真运行,利用式(10)验证3Opt算法对改进算法的运行时间和运行解精度的影响力。
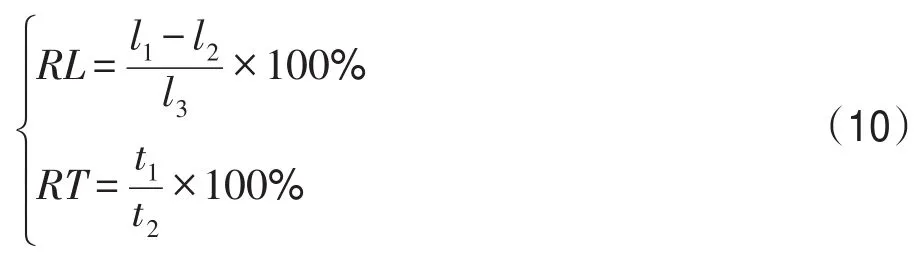

Table 3 Comparison of application of 3Opt algorithm表3 3Opt算法的运用比较
其中,RL表示路径解相对优化比例,RT表示3Opt算法运行时间占改进算法的总运行时间比例,l1表示改进算法不运用3Opt算法的解长度平均值,l2表示改进算法运用3Opt算法处理后得到的解长度平均值,t1表示3Opt算法的运行时间,t2表示改进算法的总运行时间。
从表3中可以得出,选取的6个案例运用3Opt算法处理对改进算法找到的全局路径解都起到了一定的优化作用,特别是案例fl417,路径解相对优化比例达到了31.91%。虽然案例eil51优化力度最小,仅为1.72%,但是RT值最小,仅为0.01%,可以忽略不计。随着案例规模的增大,运用3Opt算法处理显现出的优势越发明显,并且RT值的增幅放缓。
从图6可以得出,左侧的全局路径线路图在未经过3Opt算法处理前,存在3处路径线路重叠现象,右侧的全局路径线路图在经过3Opt算法处理后,原先存在的3处重叠不存在了。因此经过3Opt算法的处理,可以将改进算法运算得出的全局路径线路的边缘重叠问题消除,减少路径的总长度,从而得到更好的全局最优解。虽然3Opt算法提供了很好的路径优化方案,但是运用3Opt算法增加了改进算法整体的运行时间,参考式(11)可以得出3Opt算法的时间复杂度为O(n3)。
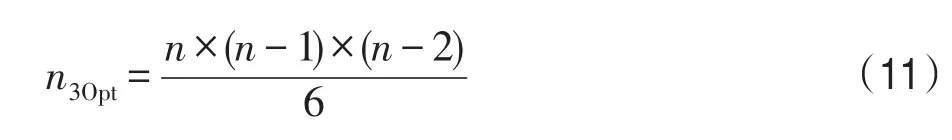
其中,n3Opt表示在3Opt算法中,需要检查边节点交换的次数,n表示城市节点数量。

Fig.6 3Opt algorithm optimization case kroA200图6 3Opt算法优化案例kroA200
为了让改进算法加快解决TSP问题的时间,必须优化3Opt算法处理进程。3Opt算法是在重复地做着同一件事,比较三边长短,然后新构造的边短就会重新更新路径,否则不会更改。因此通过加速这些单一步骤,整个改进算法的运行时间将会缩短。CPU并行方法是预先将节点与节点间的距离计算好存储在缓存内存中,这种处理方法会随着问题规模的增大而降低效率,并且也会受到内存带宽的限制。故本文参考文献[16]中的GPU并行方法,利用GPU内存存储城市的坐标,并且存储在共享内存的快速片上,需要时就计算两城市间的距离,从而提高了数据读取速率。随着TSP问题规模的增大,GPU处理进程中计算两城市间的距离的比例会降低,这是由于快速片具有共享性,并且相比于CPU并行方法,GPU并行方法具有更高的峰值内存吞吐量。
从表4可以得出,当TSP问题集选取案例较小时,比如eil51、berlin52,除蚁群算法外,DP-ACS算法与其他两种算法的实验结果相差不大,几乎相同,并且算法均能找到eil51、berlin52问题的最优路径解,解值分别是426、7 542。虽然说eil51和berlin52问题的城市点数几乎相同,但是从它们的最优路径解值可以看出它们各自的城市点位置分布稀疏情况不同,eil51的城市点与点之间更为靠近,berlin52的城市点与点之间更为疏远。当通过改进的聚类算法对问题集berlin52进行聚类处理后,可以将问题中的城市点进行分类,划分到一类簇中。然后根据粒子群算法优化后的参数α和β交由改进后的蚁群算法进行运算处理,这样可以节约蚂蚁判断前往下一个城市的运算时间。因为由蚁群算法状态转移规则可知,两个城市间的间隔越短,蚂蚁从当前城市去往间隔短的城市的概率就会越大,密度峰聚类就是把离中心节点最近的城市化为一类,那么在这一类中的节点与节点之间的距离远远小于与其他类中的节点距离。
本文选取5组小规模TSP问题集,即eil51、berlin52、eil76、kroA100、ch150,用改进算法进行仿真实验,每组TSP问题分别实验20次,并将DP-ACS算法的实验结果与 ACO[17]、ACO+3Opt[5]、PSO+ACO+3Opt[6]进行比较。蚁群算法中参数α与β值的选取参考表1中的6个小规模TSP问题对应的参数值设置。
从表4可以得出,针对eil51问题,DP-ACS算法在找到问题最优路径解值的前提下,标准差较ACO[17]降低了3.72,这说明DP-ACS算法更加稳定,实验仿真结果的波动性更小。针对kroA100问题,DP-ACS算法与其他算法相比,平均值分别降低了1 581.66、28.34、146.64。DP-ACS算法在20次仿真实验中得出的最优路径解值更接近问题已知最优解,因此DPACS算法的解精度更高一些,并且较ACO[17]、PSO+ACO+3Opt[6],DP-ACS算法可以找到问题已知最优路径规划。在标准差值中,DP-ACS算法比其他算法低211.73、10.27、54.79,得出DP-ACS算法具有更高的稳定性,算法每次找到的最优路径解偏差较小,改进算法具有更强的鲁棒性能。针对ch150问题,DPACS算法找出的最优路径解与已知最优解值相差只为5,与已知路径最优解值几乎相同,比ACO[17]找到的路径最优解缩小了115.51,比ACO+3Opt[5]找到的路径最优解缩小了37,比PSO+ACO+3Opt[6]找到的路径最优解缩小了5,DP-ACS算法较大程度上提高了算法的解精度,改进算法在平均值和标准差上都比其他算法更优,故DP-ACS算法具有更强的稳定性。
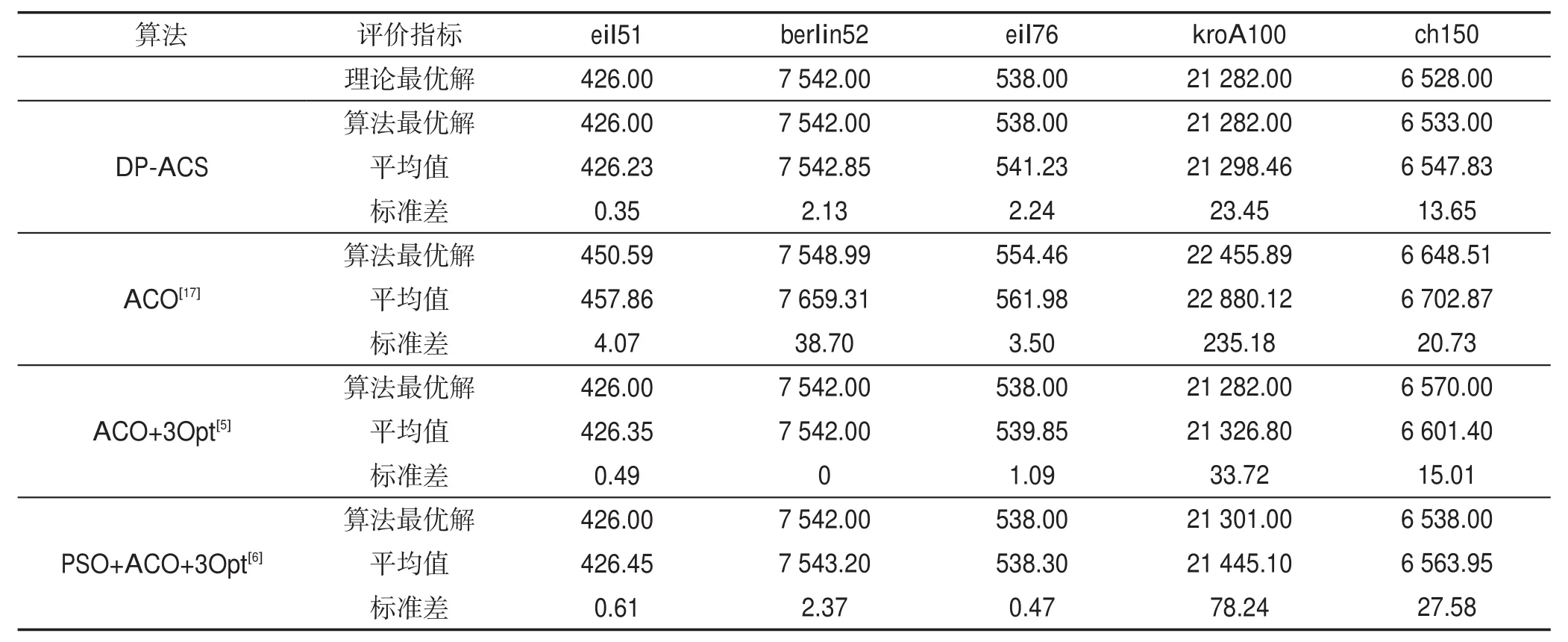
Table 4 Comparison of DP-ACS algorithm with other algorithms on small-scale TSP instances表4 DP-ACS算法与其他算法在小规模TSP案例上的比较
4.2 DP-ACS算法处理大规模TSP问题
本文选取4组大规模TSP问题集,即kroA200、rd400、fl417、d493,用DP-ACS算法进行仿真实验,每组TSP问题分别实验20次,并将DP-ACS算法的实验结果与 ACO+3Opt[5]、PSO+ACO+3Opt[6]进行比较。ACO中参数α与β值的选取参考表1中的TSP问题对应的参数值设置。
对于大规模的TSP问题,通过密度峰聚类算法处理后得到的簇中包含的数据集节点限制在40个以内[15]。然后经过蚁群算法运算后各自形成的二类TSP问题的路径图,这些簇与簇之间交流的时间很短,通过找到两个聚类簇之间最近邻节点,然后切割重组成初始TSP问题的最优路径图。对于大规模的TSP问题,运用密度峰聚类算法和不运用密度峰聚类算法之间的差别是显著的,特别在算法运行时间上的减少是明显的。
由表5可以得出,与ACO+3Opt[5]、PSO+ACO+3Opt[6]相比,DP-ACS算法找到了案例kroA200的最优路径解,并且在平均误差百分比(平均值与理论最优解的差值除以理论最优解)上降低了0.7%,因此DP-ACS算法运行更加稳定。在案例rd400、fl417上,DP-ACS算法的平均误差百分比分别降低了1.28%、1.79%、0.66%、0.6%,DP-ACS算法在每个TSP案例中的20次仿真实验结果精度更高,解路径值更加接近TSP案例的理论最优解。在案例d493上,DP-ACS算法的运算结果精度有所提高,较其他算法的最优解值,DP-ACS算法找到的最优路径分别缩短了382、436。
对于大规模的TSP问题,经过改进的密度峰聚类算法处理后,得到的二类TSP问题城市节点数量较初始TSP问题更少,这样减轻了具备自适应信息素更新机制的蚁群算法的运算复杂度。相对于大规模TSP问题,蚁群算法解决二类TSP问题更容易找到全局路径最优解,对于蚂蚁在寻找自身的局部最优解的时候,城市节点数量越少,蚁群更加容易找到局部最优路径,密度峰聚类算法的运用加快了蚁群算法在处理二类TSP问题的收敛速度,并且由于城市数量的减少,蚁群算法[18]不易陷入局部最优。当全局路径线路经过3Opt算法处理后,进一步优化算法已知最优路径解,有效地提高了解精度,本文在构建局部最优路径路线的基础上优化了全局最优路径路线。
4.3 算法收敛速度与多样性分析
选取4个TSP问题的基本案例,kroA100、ch150、kroA200、fl417,将 DP-ACS算法与蚁群算法(ant colony system,ACS)、最大-最小蚁群算法(max-min ant system,MMAS)进行仿真实验对比。

Table 5 Comparison of DP-ACS algorithm with other algorithms on large-scale TSP instances表5 DP-ACS算法与其他算法在大规模TSP案例上的比较
从图7(a)可以得出,DP-ACS算法在kroA100案例中收敛速度比ACS算法、MMAS算法都快,大约在算法迭代运行了500次后,DP-ACS算法已经收敛到了全局最优解,即21 282。虽然ACS算法多样性很强,但是ACS算法并没有找到全局最优解。从图7(b)可以得出,DP-ACS算法在前180次迭代运行中,路径解都在不断经过优化,并且从迭代曲线看,每次迭代优化的数值都较大。而ACS算法自80次迭代运行开始就收敛到了算法找到的最优解,陷入了局部最优,解路径值没有再变优。MMAS算法表现出丰富的多样性,但是找到的路径最优解较DP-ACS算法还是相差甚远。从图7(c)可以得出,DP-ACS算法表现出的全局多样性更优越,ACS算法收敛速度慢并且算法找到的结果与理论最优解相距甚远。MMAS算法过早收敛到算法最优解,多样性较差,并没有找到理论最优解。从图7(d)可以得出,当所选TSP案例增大时,DP-ACS较其他算法更加优越,种群多样性更优,没有出现过早收敛的情况,而ACS算法、MMAS算法均在300次迭代后陷入局部最优,并没有有效提高算法的解精度。
图8(a)、图8(b)分别是ACS算法与DP-ACS算法在解决fl417问题所表现出的算法多样性[19]。从图8(a)可以得出,ACS算法在前200次迭代运行中,前后迭代运算的标准差呈上升趋势,种群多样性较好。但是图8(b)中DP-ACS算法所表现出种群多样性更好,DP-ACS算法在前700次迭代运行过程中,前后迭代运算的标准差一直呈上升趋势,这说明DPACS算法一直在不断优化解路径。对比图8(a)和图8(b),DP-ACS算法每次迭代运算的标准差都较ACS算法的标准差数值大,在第400次迭代时,DP-ACS算法运算出的标准差数值较ACS算法运算出的标准差相差约500,这表明了DP-ACS算法中每次迭代运行中的蚂蚁所寻找的路径解数值相距较大,DP-ACS算法表现出更好的种群多样性。
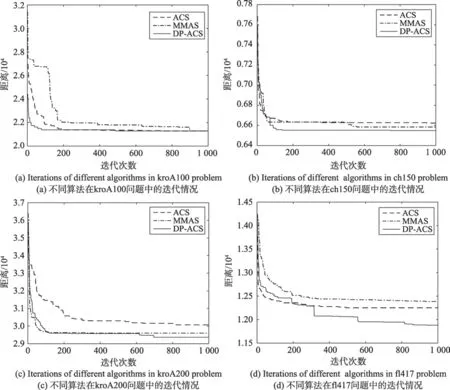
Fig.7 Comparison of algorithm iterations for different TSP problems图7 不同TSP问题的算法迭代情况比较

Fig.8 Comparison of algorithm diversity图8 算法多样性比较
4.4 分析时间复杂度
如表6所示,选取6个TSP问题案例,然后经过改进算法的运算,统计20次仿真实验,求取平均运算时间,比较改进算法与ACO+3Opt[5]算法、PSO+ACO+kOpt[20]的平均运算时间。

Table 6 Comparison of running time between improved algorithm and other algorithms表6 改进算法与其他算法的运行时间比较 s
从表6可以得出,随着案例的城市节点数量上升,3种算法的运算时间均在增大。由于ACO+3Opt[5]算法没有经过聚类[21-22]处理以及没有运用粒子群算法,因此针对eil51案例,ACO+3Opt[5]算法运算时间更短。但是,随着案例规模的增大,改进算法的运算时间显现出明显的优势。
DP-ACS算法的运行时间是衡量算法优化TSP问题性能的一个重要指标。对于单纯用蚁群算法解决TSP问题,提出式(12)来表达算法的运算复杂度。
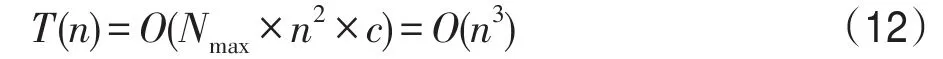
其中,Nmax是蚁群算法迭代运行的次数,n表示TSP问题规模,即城市节点总数额,c表示与n成比例的常数。
令nm表示TSP问题经过密度峰聚类算法聚类形成的二类TSP问题所能包含的最大节点数额。本文参考文献[14]将nm设置为40。提出式(13)来计算DP-ACS算法的时间复杂度。

其中,O(n1)是密度峰聚类算法对TSP问题每个节点进行计算处理的时间复杂度,O(n2)是经过3Opt算法进一步优化找到的最优路径的时间复杂度O(n3)。因为经过密度峰聚类算法处理过的TSP问题形成的二类TSP问题规模大致相同,并且每个二类TSP问题的规模都不会超过nm,所以蚁群算法处理二类TSP问题的时间复杂度为然后再乘以经过向上取整的n/nm,得出经过密度峰聚类算法处理后的蚁群算法时间复杂度O(n),其中表示聚类算法处理后形成的二类TSP问题的数额。因此,整个改进算法的时间复杂度为O(n3)。
4.5 DP-ACS算法找到的最优路径图
如图9~图12,分别是DP-ACS算法就TSP问题ch150、lin105、kroA200、fl417处理得到的算法最优路径解。

Fig.9 Optimal path for ch150 problem(length:6 533)图9 ch150问题的最优路径(最短距离:6 533)

Fig.10 Optimal path for lin105 problem(length:14 379)图10 lin105问题的最优路径(最短距离:14 379)
5 结束语

Fig.11 Optimal path for kroA200 problem(length:29 368)图11 kroA200问题的最优路径(最短距离:29 368)

Fig.12 Optimal path for fl417 problem(length:11 898)图12 fl417问题的最优路径(最短距离:11 898)
随着TSP问题规模的增大,蚁群算法在问题解精度以及算法收敛速度上表现不足[23],提出具有自适应信息素更新策略的聚类蚁群算法(DP-ACS)。利用密度峰聚类算法将原始TSP问题切割成较小的簇,这些簇再由具有自适应信息素更新策略的蚁群算法求解形成解路径。这些二类TSP问题各自形成的闭合解路径通过近邻点切割断开重组构成原始TSP问题的解路径回路,再经局部优化策略(3Opt)优化最优路径解,通过这些改进策略共同作用提高改进算法的性能。实验结果证明,DP-ACS算法的最优解精度以及收敛速度都较其他的改进蚁群算法更优越,当TSP问题规模增大的时候,DP-ACS算法的优越性更加突出。在接下来的研究过程中,将探讨蚁群算法求解二类TSP问题的解精度与算法的迭代运行次数之间的关联;另一方面,将研究二类TSP问题各自形成的解路径如何有效地连接在一起构成全局最优路径。

