利用LSTM网络和课程关联分类的推荐模型

王素琴，吴子锐

华北电力大学 控制与计算机工程学院，北京 102206

1 引言

随着互联网以及移动互联网技术的迅速发展，在线学习方式已经得到了人们的广泛认可。在线学习网站在为用户提供丰富课程资源的同时，信息过载问题日益凸显，海量的学习资源常常让用户无所适从。推荐系统能够帮助用户快速发现所需要的课程，是缓解信息过载问题的最有效方法之一[1]。

在线学习网站目前主要采用传统的协同过滤算法[2-3]为用户推荐课程，但存在冷启动[4]和数据稀疏性等问题。近年来，深度学习技术发展迅速，并率先在图像处理、自然语言处理和语音识别等领域取得突破性进展[5-6]，为推荐系统带来了新的思路。与协同过滤算法相比，多层神经网络可以更好地应对数据的稀疏性特征。其中，长短时记忆（long short-term memory，LSTM）网络擅长处理时间序列数据，当用户行为模式具有明显的时序性特点时，采用LSTM网络能够更准确地预测用户未来的行为。用户选择新的课程时要考虑的因素与网络购物差异较大，用户购买商品通常出于个人偏好[7]，但选择新的课程时，往往与其学过的课程有关，即用户所学习的课程具有一定的时序性。根据这一特性，本文将LSTM网络应用于在线课程的推荐，根据用户已学习的课程序列预测其将要学习的课程。

本文第2章介绍相关工作；第3章给出相关概念；第4章介绍课程推荐模型；第5章提出基于频繁模式谱聚类的课程关联分类模型；第6章给出在线课程推荐算法；第7章基于在线学习网站数据集进行实验结果验证和分析；第8章对全文工作进行总结。

2 相关工作

2.1 协同过滤算法及其应用

协同过滤算法是根据用户群体兴趣的相似性进行推荐的技术，分为基于用户的协同过滤推荐（userbased collaborative filtering，UCF)和基于项目的协同过滤推荐（item-based collaborative filtering，ICF）。由于在线学习网站中用户的数量通常远多于课程的数量，使得计算用户相似度矩阵的代价远远高于计算课程相似度矩阵的代价，因此针对该问题采用基于项目的协同过滤推荐算法效率更高。

冯亚丽等人[8]综合应用UCF和ICF算法进行远程培训中的个性化学习资源的智能推荐，经实际应用测试表明效果良好。李浩君等人[9]提出了基于多维特征差异的个性化学习资源推荐算法，针对推荐模型的多目标优化特征，将协同过滤算法和粒子群算法相结合，实验结果证明该算法准确率较好。

2.2 基于深度学习的推荐算法及其应用

深度学习技术能将数据的属性或者特征进行提取并抽象为更高层的表示。最早应用于推荐系统的深度学习技术是受限玻尔兹曼机[10]（restricted Boltzmann machine，RBM），Hinton等人使用RBM对表格数据建模，并提出了一种对比散度算法来提高RBM的训练效率。实验结果表明，该方法在Netflix数据集（包含超过1亿用户的评分数据）上表现出色。微软公司的研究人员Song等人[11]在WWW2015会议上提出了一个面向新闻和桌面应用的基于内容的推荐模型，采用深层神经网络（deep neural networks，DNN）进行用户信息的提取。

循环神经网络（recurrent neural network，RNN）主要用于处理序列数据。Netflix研究员Hidasi[12]提出了一个基于会话的循环神经网络推荐系统，将会话记录中的用户点击项序列信息作为输入数据，在用户点击流数据量庞大且数据稀疏性高（即大部分用户点击量往往集中在少量的数据项）的情况下，RNN网络取得了不错的推荐结果。Okura等人[13]采用RNN从用户的历史行为列表中学习用户的偏好，最后利用用户与新闻之间的关联性为用户推荐新闻。斯坦福大学Liu等人[14]比较了十种不同结构的RNN网络对用户评论信息进行处理后的推荐效果，在此基础上提出了一种适合于推荐的双向RNN结构。

2.3 基于LSTM的推荐算法及应用

LSTM网络针对RNN的隐藏层单元进行改进，具备长时记忆功能。通常来说，RNN能够解决的问题LSTM都能够处理并且效果更好。目前LSTM网络主要应用于自然语言处理、语音识别和图像理解。Graves等人[15]最早将LSTM网络应用于单词预测方面的研究，经过英语和法语语言库的训练后，单词预测正确率比标准RNN高出8%。Li等人[16]提出了一种基于LSTM网络的推特推文标签推荐系统，首先使用skip-gram模型生成词汇表，然后应用CNN（convolutional neural networks，CNN）将文章中的每一个句子生成为句子向量，最后利用句子向量训练LSTM网络。实验结果表明，与标准RNN以及GRU（gated recurrent unit）相比，基于LSTM的推荐模型取得了更好的效果。

多项研究结果表明LSTM网络适合于对具有时序性的信息流进行建模，并且在序列的时间跨度较大的情况下LSTM的性能优于RNN。

3 相关概念

3.1 RNN网络结构

循环神经网络RNN是一种时间递归网络，可以看作是同一个神经网络结构在时间轴上循环多次得到的结果。与其他深层神经网络相比，RNN的结构特点决定了它更擅长处理序列数据。

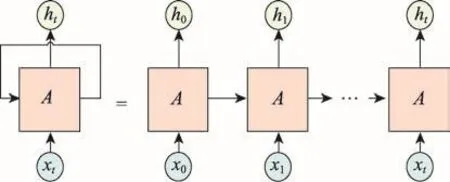
Fig.1 Network structure of RNN图1 RNN网络结构

RNN的网络结构如图1所示，其中A为RNN隐藏层处理单元，xt为当前时刻的输入值，ht为当前时刻隐藏层的输出值。从图中可以看出，ht是由当前输入值xt和上一时刻输出值ht-1共同决定，而ht又会影响下一时刻的输出，即每个输出值不仅与当前的输入值有关还与之前时刻的输出值有关。

理论上RNN可以处理任意长度的时间序列数据，但是在实际应用中发现，在RNN训练过程中会产生梯度消失和梯度爆炸的问题。Pascanu等人[17]通过详细的数学推导解释了这一现象产生的原因，即传统的RNN模型在训练时倾向于按照序列结尾处的权值正确方向进行更新。由于隔得越远的输入序列，对权值能够正确变化的影响越小，因此网络输入偏向于新信息的输入而不具备长期记忆功能。

3.2 LSTM网络结构

LSTM解决了RNN训练神经网络过程中梯度消失和梯度爆炸问题，能够保留更久以前的信息。LSTM的网络结构与RNN大体接近，但是隐藏层的结构更为复杂，如图2所示。

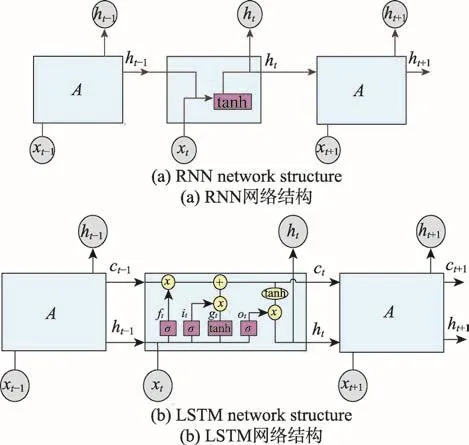
Fig.2 Comparison of RNN and LSTM network structures图2 RNN和LSTM网络结构比较

图2 中，t时刻的输入信息包括当前的输入值xt以及上一时刻的输出值ht-1。LSTM处理单元主要由输入门（用it表示）、遗忘门（用ft表示）、输出门（用ot表示）组成。

输入门it主要用于控制当前时刻信息的流入量，见式（1）。

遗忘门ft用于控制上一时刻累积的历史信息ct-1的流入量，见式（2）。

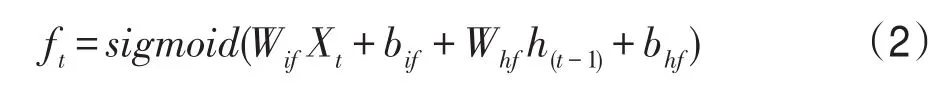
输出门ot主要用于控制当前时刻信息的流出量，见式（3）。

gt代表当前时刻信息的更新值，它由上一时刻的输出值ht-1和当前时刻的输入值xt所决定，见式（4）。

ct表示隐藏层单元携带的信息，类似于细胞的状态。它由输入门和遗忘门控制，每一时刻都在更新，并直接决定当前的输出。ht是由输出门ot对ct进行筛选后得到的输出结果，见式（5）、式（6）。

以上公式详细地推导了输入信息在LSTM隐藏层的处理过程。LSTM通过输入门、遗忘门和输出门三个门的作用来调控信息的流向以及筛选信息，从而解决了信息的长时记忆问题[18-20]。

4 基于LSTM网络的在线课程推荐模型

4.1 在线课程推荐模型的框架

基于LSTM的在线课程推荐模型按照功能划分为输入部分、处理部分和输出部分，如图3所示。

输入部分将用户的原始学习记录转化为LSTM网络计算时所需要的数据形式，即每个用户已学课程的向量表示。

处理部分是通过LSTM网络处理输入数据，得到输出结果。需要确定LSTM网络的结构，包括网络层数、时间步长以及各层之间的连接设置。本文以课程的数量作为特征值的数量，相应地也就定义了输入数据和输出数据的维度，即输入层和输出层神经元的数量。用户的课程学习序列长度决定了每次计算时的时间步长，将最大时间步长定义为用户学习的课程序列的最大值，同时在读取每个用户学习序列时，需要指定相应的序列长度。这样整个LSTM网络模型的结构就确定了。Softmax层是将LSTM处理层输出向量的值映射到（0,1）区间内。

输出部分取Softmax层处理结果的最后一个维度得到最终推荐的课程向量。

4.2 课程向量表示及输入数据预处理

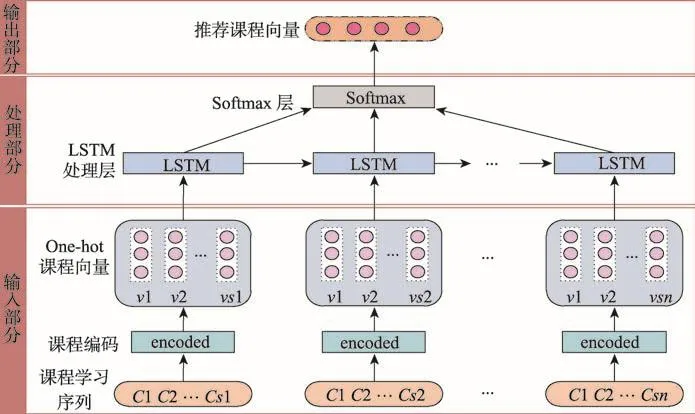
Fig.3 Framework of online course recommendation model图3 在线课程推荐模型框架

神经网络在计算前通常需要对输入数据进行归一化处理，将数据限制在一定范围内，以保证模型能够迅速收敛。本文采用One-Hot编码对输入数据进行归一化处理。One-Hot编码采用二进制向量形式，因此需要将课程映射为整数值，即每一门课程对应一个课程id，再将课程id表示为二进制向量，向量中下标为id号的元素值标记为1，其他元素都是0，例如{0,0,0,1,0…0}表示课程id为4的课程。对输入数据进行预处理的过程如图4所示。

首先读取数据库中用户原始学习记录，并转化为用户-课程序列的格式，最后将课程序列中每一门课程用向量表示。

其中将用户课程序列用向量表示的方法如图5所示。

Fig.5 Data normalization diagram图5 数据归一化处理示意图

4.3 模型输出和推荐结果

将样本中每个用户的课程学习序列输入到模型中，经过LSTM网络处理后，再通过Softmax层映射得到最终的推荐结果，如图6所示。

输出结果是向量形式，每个元素的下标代表相应的课程id，每个元素的值表示用户学习该课程的概率。向量中最大元素的下标即为推荐给用户的课程id，是用户接下来最有可能学习的课程。

4.4 模型输出和推荐结果

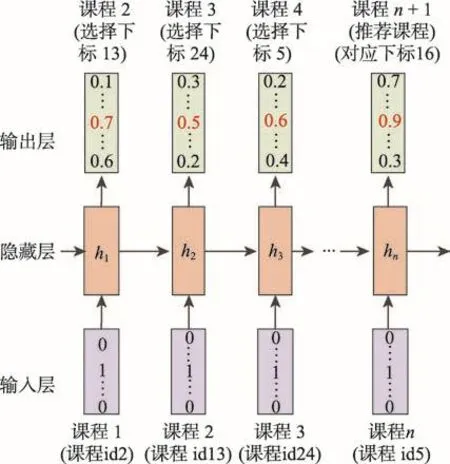
Fig.6 Input and output of model图6 模型输入输出示意图

训练神经网络时，使用损失函数（loss function）来评估模型的预测值与实际值不一致的程度。损失函数的值越小，模型的性能越好。交叉熵损失函数适用于多分类和预测问题。根据在线课程推荐的特点，本文选用交叉熵损失函数作为LSTM网络的损失函数，其计算方法如式（7）所示。

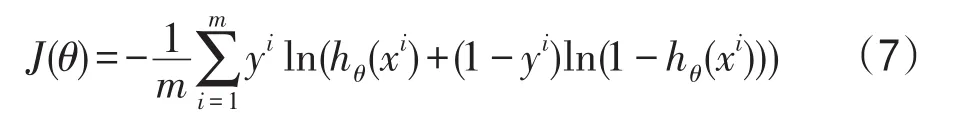
式中，m表示样本大小，xi表示第i组输入值，yi表示第i组输入值对应的实际值，hθ表示模型中的权值参数，hθ(xi)表示模型的输出值。

交叉熵损失函数有两个重要的性质：

（1）非负性：J(θ)的值始终大于0，优化函数的目标是将函数值减小。

（2）模型的输出值hθ(xi)与实际值yi偏差越小，J(θ)的值越小。当神经网络的输出值接近于实际值时，J(θ)的值接近于0。

以上两个性质说明了交叉熵损失函数从数学的角度上看，适合用来评估模型的性能。当选择sigmoid函数作为激活函数时，权值的更新速度与误差大小相关，避免了反向传播损失值收敛速度慢这一问题[21]。

4.5 Adam优化算法

在训练神经网络时，需要使用优化算法来调整网络的权值参数，减小损失函数的值，使模型的性能得到优化。常用的优化算法有SGD算法、Adagrad算法和Adam算法等。SGD算法在每次迭代时计算最小batch的梯度，然后更新参数，缺点是选择合适的学习速率比较困难，且容易陷入局部最优解。Adagrad算法对学习速率进行了约束，但仍依赖人工设置全局的学习速率，有时对梯度的调节过大。Adam（adaptive moment estimation）算法适用于大数据和高维度的空间，对内存的需求较小，因此本文采用Adam算法作为优化算法。

Adam算法能够根据损失函数对每个参数的梯度的一阶矩估计和二阶矩估计动态调整针对于每个参数的学习速率。Adam是基于梯度下降的方法，但是每次迭代参数的学习步长都有一个确定的范围，不会因为较大的梯度导致过大的学习步长，参数更新比较稳定。Adam的每一步迭代过程如下：

（1）从训练集中随机抽取一批样本{x1,x2,…,xm}以及相应的输出yi。

（2）计算梯度和误差，更新一阶动量s和二阶动量r，再根据s和r以及梯度计算参数更新量。

与其他自适应学习率算法相比，Adam算法收敛速度更快，学习效果更有效，能够解决其他优化算法中存在的问题，如学习率消失、收敛过慢或是高方差的参数更新导致损失函数波动较大等[22]。

5 基于频繁模式谱聚类的课程关联分类模型

5.1 关于课程分类的讨论

上文的课程推荐算法是基于课程之间的时序性而提出的，因此将课程按照时序相关性进行分类后推荐的准确率会更高。目前，在线学习网站课程的分类由人工进行，一般只是单纯地依据课程内容上的相似性，对课程学习的时序相关性考虑不多。同时，由于在线课程更新频繁，人工维护课程分类的工作量较大。如果能够根据大量用户的学习记录发现课程之间的时序相关性，再依据时序相关性对课程进行自动分类，必将进一步提高推荐算法的准确性。这里的课程分类不是通常意义上的课程聚类，聚类是根据课程的特征值计算课程间的“距离”，反映的是课程的相似性，而这里的课程分类考虑的是课程的时序相关性。本文采用GSP（generalized sequential pattern mining algorithm）算法和谱聚类算法对课程进行分类。

5.2 GSP算法和课程关系建立

首先使用GSP算法从用户课程学习记录数据库中挖掘出不同课程之间的关联关系，为下一步的聚类决策提供支持。GSP算法是一种常用的序列模式挖掘算法[23]，属于Apriori类算法。它能够从用户对课程的学习行为中，发现常见的学习模式，挖掘出课程之间时序上的联系。

首先应用GSP算法挖掘出数据库中所有超过最小支持度阈值的频繁项集。对课程序列α支持度的定义见式（8）。

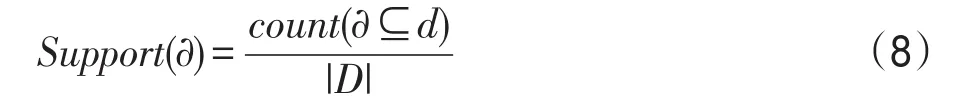
式中，count(α⊆d)表示数据库中包含课程序列α的用户课程序列d的个数，|D|表示数据库大小，即序列总数。最小支持度阈值Supmin是人为设定的。

再对频繁项集进行连接操作，设有两个序列s1和s2，若s1去掉第一项和s2去掉最后一项剩下的序列相同，便可进行连接操作。通过连接操作自下而上地进行迭代产生更长的高阶频繁序列。

算法的实现流程如下所示：

（1）输入用户-课程数据库D，支持度阈值Supmin。

（2）扫描数据库，产生长度为1的频繁序列的集合，即种子集L1。

（3）对频繁序列进行连接，删掉不满足支持度阈值的序列，直到没有新的候选集产生时，结束。

（4）输出频繁模式L，支持度列表count。

GSP算法挖掘出的频繁序列数量随着序列长度的增加呈现指数级递减。较长的频繁序列数量稀少，无法用于课程的分类。因此根据GSP算法挖掘出的长度为2的频繁序列，建立课程关联矩阵W。W是一个对称矩阵，其中Wij表示课程i与课程j的关联度,设定Wii=0。对于频繁模式 ＜i,j＞，对应的支持度为a(a＜1)，那么Wij=Wji=a。

5.3 谱聚类算法和课程关联分类

GSP算法得到的关联矩阵只能提供两个课程间的相关程度，需要利用谱聚类算法[24]进一步根据课程关联关系的强弱对所有课程做出合理的簇划分。谱聚类算法是在传统聚类算法的基础上结合了图谱理论而演化出的算法，后来在聚类中得到了广泛的应用。其基本原理是：对于一个图G，通常需要用点的集合V和边的集合E来进行描述，记作G(V,E)。V为样本集中的所有点(v1,v2,…,vn)，对于图中的点，定义Wij为点vi和vj之间的权重。谱聚类算法简单地说就是通过对所有数据点组成的图进行切图，让切图后不同子图点之间的权重较低，子图内点之间的权重尽可能得高，从而达到聚类的目的。而最优的切图方式，则可以通过对无向图邻接矩阵进行数学变化得到[25]。

本文将各个课程当作顶点，课程数为n，课程间的关联度Wij看成带权重的边。算法流程如下：

（2）求出L前k个较小特征值对应的特征向量，构造N×K维特征向量矩阵M，其中N为全部课程数，K为指定特征数。将全部课程投影到k维空间，M的每一行表示每门课程对应的k个特征。

（3）将每一行作为一个样本点，对N个样本点进行K-means聚类，最终得到每个课程的分类结果。

6 基于课程关联分类和LSTM网络的课程推荐流程

（1）利用GSP算法从用户课程学习记录表中挖掘出频繁序列，并根据支持度建立课程关联矩阵。

（2）应用谱聚类算法在课程关联矩阵的基础上对所有课程分类。

（3）数据归一化，通过one-hot编码将课程序列转化为课程向量集合。

（4）按类别将课程向量输入推荐模型，得到输出结果。

（5）通过交叉熵损失函数，将模型的输出结果与实际值比较，计算偏差值。

（6）偏差值反向传播，应用Adam优化算法更新模型中每一层神经元的权值参数，达到调整偏差值的目的，直到满足指定的条件，否则重复（3）、（4）、（5）步骤。

（7）推荐模型训练结束后，载入测试数据，得到模型的输出值，获取推荐结果。

7 实验结果及分析

7.1 实验数据集

实验数据集来自于某在线教学网站的实际运行数据，用户数13 680人，课程总数737门，主要是计算机类相关课程。数据包括用户的学习记录和评分记录，时间跨度从2014年5月到2017年7月，记录总条数共148 170条。其中训练集占80%，约11.8万条记录，测试集占20%，约3万条记录。首先将数据简化为三元组（用户id,学习时间,课程id）。

7.2 评估指标

算法的评价指标是准确率（Precision），是指在推荐给用户的所有课程中用户实际学习的课程所占的比例，见式（9）。

式中，T(u)表示用户u实际学习的所有课程，R(u)表示推荐给用户u的所有课程。准确率越高，表示推荐的课程越符合用户的期望。

7.3 实验结果

输入测试集中用户已学习的课程序列，经模型处理后输出一个课程序列，取最后一门课程作为用户推荐课程，并与用户实际学习的课程相比，判断推荐结果是否准确。

7.3.1 人工分类和频繁模式谱聚类下推荐结果对比

将全部课程人工划分为前端开发、后端开发、数据库应用、软件测试、UI设计、移动端开发六大类，并相应地将数据集拆分为六个子集。

表1记载了网站人工分类下应用基于LSTM推荐算法的推荐结果。

Table 1 Recommend results based on artificial classification of websites表1 基于网站人工分类下的推荐结果

从表格中可以看出，分类后各个类别下的推荐结果普遍好于全部课程下的推荐结果。

采用频繁模式谱聚类算法进行课程的自动分类，得到六个课程类别，相应的推荐结果如表2所示。

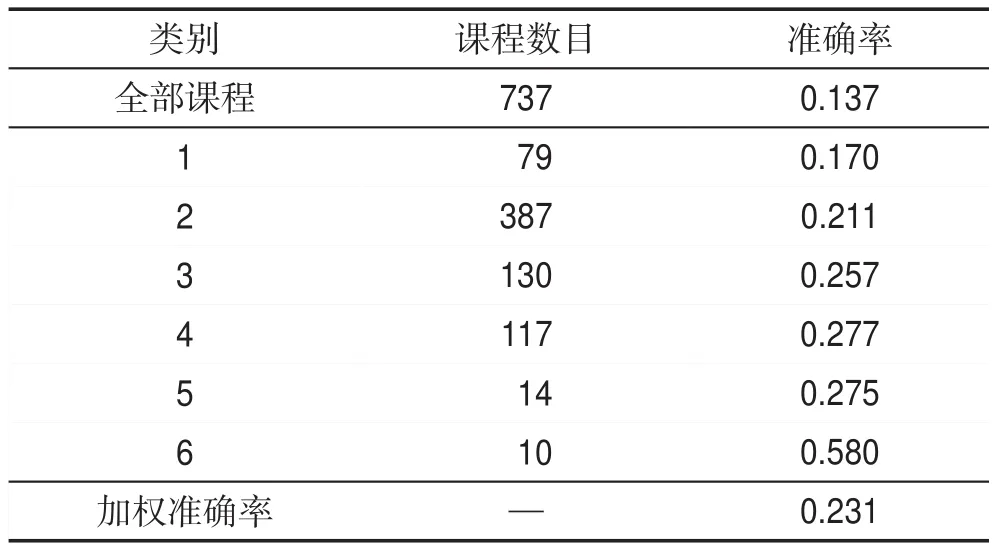
Table 2 Recommended results based on spectral clustering表2 谱聚类下的推荐结果

与表1人工分类推荐结果对比，推荐算法在谱聚类划分的大多数类别下比人工分类的表现更好，加权的准确率提高了1.7%。

7.3.2 与协同过滤推荐算法对比

本文算法与UCF和ICF算法在相同数据集下的推荐结果准确率比较如表3所示。

除了全部课程类别外，本文算法的准确率指标均远远高于ICF和UCF算法。与协同过滤算法相比，本文算法更适合于时序依赖性较强的课程的推荐。另外，ICF比UCF更适合于在线教学网站中用户数量远大于课程数量情况下的推荐工作。

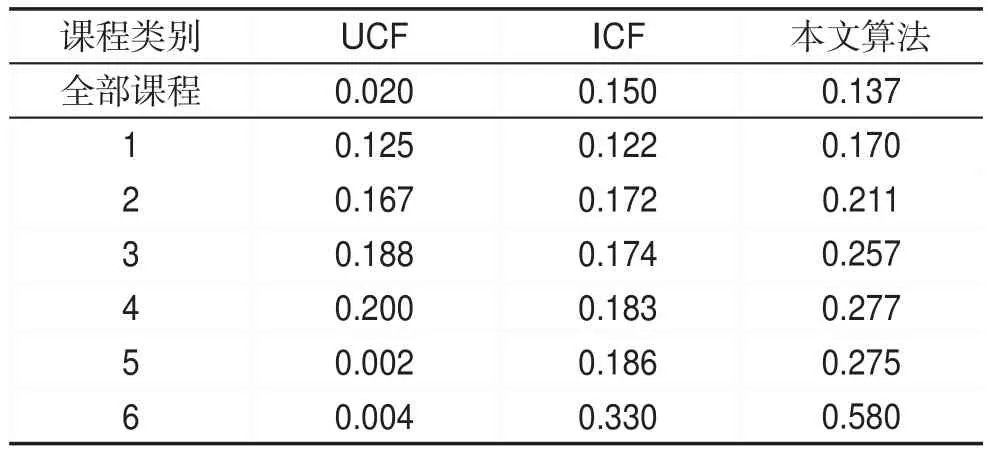
Table 3 Precision comparison between this algorithm and collaborative filtering recommendation algorithm表3 本文算法与协同过滤推荐算法准确率的对比

7.3.3 与基于RNN的推荐算法对比

基于RNN网络的推荐算法与本文算法在相同训练周期下（设定为100）推荐结果的准确率比较如表4所示。

Table 4 Precision comparison between this algorithm and recommendation algorithm based on RNN表4 本文算法与基于RNN的推荐算法准确率的对比

实验结果表明，一方面，两个算法在不同类别课程上表现的差异性是相似的，在课程之间联系比较紧密的课程类别上算法的表现更好，反之则算法的表现稍差；另一方面，在每一个课程类别上本文算法的推荐效果都优于RNN推荐算法，在用户课程学习序列普遍较长的情况下两者表现差距更大，出现这种现象的原因是LSTM网络具备长时记忆功能，能够很好地利用关系紧密的序列信息。

8 总结

本文结合了LSTM网络的特性和在线课程学习的特点，提出将LSTM网络应用于在线课程推荐算法，并应用GSP算法和谱聚类算法对全部课程进行分类，使每一类别下的课程联系更加紧密。实验结果表明，自动分类方法提高了课程推荐的准确率。与传统的协同过滤算法相比，对于同类课程的推荐本文算法准确率有大幅度提升；与RNN推荐算法相比，本文算法在各个类别的课程数据集上准确率均有明显提升，在用户课程学习序列普遍较长的情况下，两者表现差距更大，体现了LSTM网络具备长时记忆的优势。实验结果表明，本文算法具有准确率高，所推荐课程与用户已学课程密切相关的优点。

本文算法存在的不足主要是推荐列表的长度过短。本文算法推荐课程时取的是LSTM网络输出序列的最后一个维度，对应的是出现概率最大的课程，因此推荐列表的长度只有1，在实际推荐系统中，往往需要更多的推荐结果，在后续改进时，可选择出现概率大的多门课程进行Top-N推荐。