多类分类模型和多层次增量算法*

2019-08-12 02:11王旭生

计算机与生活 2019年8期

徐怡，王旭生

1.安徽大学计算智能与信号处理教育部重点实验室，合肥 230039

2.安徽大学计算机科学与技术学院，合肥 230601

1 引言

三支决策作为决策粗糙集和粒计算理论的一个重要应用方向[1-2]，是研究不确定性决策的有力工具，广泛应用于知识发现、数据挖掘和模式识别等领域[3-5]。相比于传统的二支决策，三支决策的关键是引入了延迟决策，从而规避了错误决策造成的损失。当做出延迟决策时，为了下一次做出准确决策，需要进一步采集决策的状态信息，即对决策对象的认识从粗粒度向细粒度进行转化。这种从粗粒度到细粒度的决策过程构成了一种序贯决策方法[6-7]，它可以刻画人们在许多实际问题中所采用的动态渐进决策过程。例如，在医学诊断中，初步检查后仍无法判断患者患有哪种疾病，此时需要通过其他的手段对患者逐步进行检查，直到最终确定患者病情，并给出相应的治疗方案。

三支决策作为一种决策方式，其主要用于二分类问题。然而实际应用中会经常出现多分类的问题，例如病毒性肝炎、流行性感冒、肺炎、扁桃体炎等疾病类型的判定等多类分类问题，而关于多类分类问题下的模型较少。Yao和Zhao[8]将m分类问题转换成m个二分类问题，并为每个决策类做出三支决策。Ślęzak[9]将贝叶斯模型应用到分类问题中，基于成对比较的决策类来处理多类分类问题。Liu等[10]提出了基于决策粗糙集的两阶段多分类问题来决定最佳决策。Zhou[11-12]提出了多类分类模型需要3m×m代价矩阵来计算多类分类中的阈值。然而，上述研究只考虑了单层粒度，没有将决策结果的代价和决策过程一起考虑，在决策过程中造成较大的决策损失。为了解决这种问题，Yao[6]提出了序贯三支决策。基于信息和知识粒度，序贯三支决策致力于分层粒度结构下有效问题处理。例如，Li等[13-14]将序贯三支决策方法应用到代价敏感脸部识别问题中，并研究了基于序贯粒度特征提取的深度神经网络。Yang等[15]提出了序贯三支决策的模型并给出其增量方法。Li等[16]引入序贯三支决策的思想并提出三支决策的形式概念分析。

综上所述，本文将序贯三支决策应用到多类分类问题。通过新增属性来确定每一层的条件属性，然后在Zhou提出的模型基础上，计算每个决策类的三支决策。将边界域与负域中的对象作为下一层需要决策的对象，直到不能再添加新的属性信息，整个序贯过程结束。最后，基于本文的序贯三支决策的多类分类模型给出它的增量算法，通过仿真实验证实了本文所提算法的有效性。

2 基础概念

本章给出决策粗糙集和三支决策相关的知识[17-19]。

假设给定一个信息系统S=(U,AT,V,f)，Ω={w1,w2,…,wm}为m个有限的状态集，A={a1,a2,…,an}为n个有限的行动集。x为论域U中的对象，Pr(wi|x)表示x在状态wi下的条件概率，λ(aj|wi)表示在状态wi下采取行动aj的损失函数，则x执行决策aj的期望损失为：

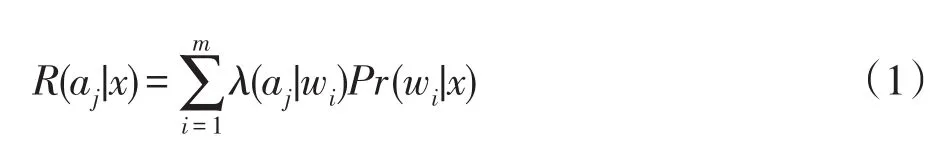
一般地，对于给定的描述x，令τ(x)为一个决策规则，ℜ为τ下的总体期望风险，则可表示为：

式中，Pr(x)为x的先验概率，R(τ(x)|x)为采取不同行动x的条件风险。根据贝叶斯的决策准则，选取使得总体期望风险ℜ达到最小的决策行为作为最佳行动方案。

基于决策粗糙集的思想，三支决策利用两个状态集和三个行动集来描述决策过程。状态集D={X,¬X}，行动集A={aP,aB,aN}，其中，aP、aB、aN分别表示将对象划分到正域POS(X)、边界域BND(X)、负域NEG(X)三种决策行为。λPP、λBP、λNP表示当样本x真实属于X类时，分别做出aP、aB、aN三种决策所对应的损失函数，λPN、λBN、λNN表示当样本x真实属于¬X类时，分别做出aP、aB、aN三种决策所对应的损失函数，该三种决策的期望损失分别表示为：

在式（3）中，[x]表示样本的等价类。选择期望损失最小的行动集作为最佳行动方案，因此得到如下三条决策规则：

（P）如果R(aP|[x])≤R(aB|[x])且R(aP|[x])≤R(aN|[x])，则令x∈POS(X)；

（B）如果R(aB|[x])≤R(aP|[x])且R(aB|[x])≤R(aN|[x])，则令x∈BND(X)；

（N）如果R(aN|[x])≤R(aB|[x])且R(aN|[x])≤R(aP|[x])，则令x∈NEG(X)。

¬X是X的补集，Pr(X|[x])+Pr(¬X|[x])=1。从式（1）中可知，决策规则只和Pr(X|[x])及λ∙∙(∙=P,B,N)有关。考虑到实际决策过程，一个合理的假设为0≤λPP≤λBP＜λNP，0≤λNN≤λBN＜λPN，因此上述的三条决策规则改写为如下形式：

（P1）如果Pr(X|[x])≥α且Pr(X|[x])≥γ，则令x∈POS(X)；

（B1）如果β＜Pr(X|[x])＜αx，则令x∈BND(X)；

（N1）如果Pr(X|[x])≤β且Pr(X|[x])≤γ，则令x∈NEG(X)。

阈值α、β、γ与决策的损失函数密切相关，具体的推导过程以及关于阈值的讨论参见文献[2]。

3 基于多类分类的序贯三支决策模型

本章将讨论序贯三支决策在多类分类问题中的应用。首先，给出序贯三支决策的基本概念和定义；然后，结合Zhou提出的多类分类模型，提出一种基于多类分类的序贯三支决策模型；最后，给出该模型的相关算法和实例。

定义1给定决策表Si=(Ui,ATi=Ci⋃Di)，其中i=1,2,…,m，Ui是一个非空的有限集合。Ci是条件属性集，满足C1⊂C2⊂…⊂Cm⊆AT。多层次粒结构记为GS，GS的第i层记为GSi，分别表示为：

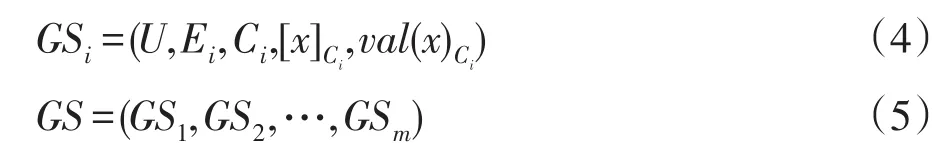
其中，Ei表示第i层下的等价关系，val(x)Ci表示x(x∈U)在第i层下的条件属性集值，[x]Ci表示其等价类且[x]Ci={y∈U|val(x)Ci=val(y)Ci}。

在多层粒结构下，第k层的决策表为Sk=(Uk,ATk=Ck⋃Dk)，第k+1层的决策表为Sk+1=(Uk+1,ATk+1=Ck+1⋃Dk+1)。下面给出从第k层到k+1层多类分类问题的处理方法。

定义2给定决策表Sk=(Uk,ATk=Ck⋃Dk)，πΩ=表示根据决策属性Dk划分的n个类，则类的正域、边界域和负域分别为：

其中，(αi,βi)为的阈值，计算方法如下。

定义3给定n个类的损失函数矩阵定义为3×m的矩阵，如表1所示。

Table 1 Loss functions matrix of表1 的损失函数矩阵

定义4给定决策表Sk=(Uk,ATk=Ck⋃Dk)，其中，给定3n×n的损失函数矩阵Costk。根据式（1），对象x采取不同行动的期望损失为：

类似于三支决策的阈值计算过程，多类分类中每个决策类的阈值为：

在多类分类问题处理中，当对象x分类到

定义6给定多层次粒结构GS的第k层GSk=(Uk,Ek,Ck,[x]Ck,val(x)Ck)，Uk的正域、负域和边界域分别为则第k+1层的Uk+1和定义为：

计算出Uk+1和，然后通过增加新的属性得到条件属性集Ck+1，因此第k+1层的决策表Sk+1=(Uk+1,ATk+1=Ck+1⋃Dk+1)。类似于第k层的分类方法，计算出第k+1层的正域、负域和边界域。此时，第k层向第k+1层的分类过程结束。在多层粒结构中，基于此分类过程对论域做出决策，直到整个序贯过程结束。

定理1给定m层粒结构GSi=(Ui,Ei,Ci,[x]Ci,val(x)Ci)，对应决策表Si=(Ui,ATi=Ci⋃Di)，i=1,2,…,m。Ci是Ui的条件属性集满足C1⊂C2⊂…⊂Cm⊆AT，Ei是Ui的等价关系满足Em⊂Em-1⊂…⊂E1。是根据决策属性Di划分的n个类。是第k层的一个类集合，是第k+1层的类集合，。从第k层向第k+1层处理时，对于∀x∈Uk，如果，则对象x的条件概率变化情况如下：

（1）如果|[x]Ck+1|=|[x]Ck|，则：

算法1基于多类分类的序贯三支决策算法

输入：决策表S=(U,C⋃D)，损失函数矩阵Costi，i=1,2,∙∙∙,m。

输出：确定到决策类的对象X。

下面给出一个例子说明算法1的计算过程。

例1给定决策表S=(U,AT=C⋃D)，其中U={x1,x2,x3,x4,x5,x6,x7,x8,x9,x10}，C={c1,c2,c3}。根据决策属性D划分得到πD={D1,D2,D3}，D1={x1,x4,x5,x8}，D2={x2,x3,x10}，D3={x6,x7,x9}。第一层中以第一个属性作为条件属性，后面依次通过增加一个属性作为下一层的条件属性，因此构建三层粒结构(GS1,GS2,GS3)。给出GS1的损失函数矩阵Cost1，如表2所示，GS2损失函数矩阵Cost2，如表3所示，GS3的损失函数矩阵Cost3，如表4所示。

Table 2 Loss functions matrixCost1表2 损失函数矩阵Cost1

Table 3 Loss functions matrixCost2表3 损失函数矩阵Cost2

Table 4 Loss functions matrixCost3表4 损失函数矩阵Cost3

4 基于多类分类的序贯三支决策增量算法

基于多类分类的序贯三支决策问题处理中，m层粒结构(GS1,GS2,…,GSm)，第k层表示为GSk=(Uk,Ek,Ck,[x]Ck,val(x)Ck)，第k+1层表示为GSk+1=(Uk+1,Ek+1,Ck+1,[x]Ck+1,val(x)Ck+1)。下面将给出从第k层到第k+1层多类分类问题处理的增量方法。

定理2基于序贯三支决策的多类分类处理中，m层粒结构GS=(GS1,GS2,…,GSm)，GSi=(Ui,Ei,Ci,[x]Ci,val(x)Ci)，对应决策表Si=(Ui,ATi=Ci⋃Di)，i=1,2,…,m。Ci是Ui的条件属性集满足C1⊂C2⊂…⊂Cm⊆AT，Ei是Ui的等价关系满足Em⊂Em-1⊂…⊂E1。那么对于Uk+1中的对象，有[x]Ck+1⊆[x]Ck。

基于序贯三支决策的多类分类处理中，m层粒结构GS=(GS1,GS2,…,GSm)，GSi=(Ui,Ci,[x]Ci,val(x)Ci)，i=1,2,…,m。Ci是Ui的条件属性集满足C1⊂C2⊂…⊂Cm⊆AT，Ei是Ui的等价关系满足Em⊂Em-1⊂…⊂E1。那么从GS的第k层到第k+1层，有因此第k+1层的等价类[x]Ck+1可以通过第k层的等价类[x]Ck和新增属性Ck+1-Ck推导得到，不需要通过Ck+1中所有属性来重新计算。当存在，因此在第k+1层不需要重新计算Uk+1中的所有对象的。此外，当=∅时，则不需要再计算，直接记为0。综上，下面给出多类分类增量算法如下。

算法2基于序贯三支决策的多类分类增量算法

输入：决策表S=(U,C⋃D)，损失函数矩阵Costi，i=1,2,…,m。

输出：确定到决策类的对象X。

使用非增量算法1和增量算法2构建的X是相同的，但是通过增量算法2计算出的X比非增量算法1计算出的X更简单。接下来通过仿真实验来验证算法2比算法1效率更高。

5 实验分析

本章将通过实验证明，在多层粒结构下，根据本文提出的多类分类模型，有效地将论域中的对象划分到决策类中。此外，在分类过程中，使用算法2计算决策类中的对象数比使用算法1更有效。

本文选取4个UCI数据集用于算法的验证，数据集的信息如表5所示。在实验中，将每个数据集的属性集分成4个属性子集用于构建多层粒结构。例如，第1个属性子集作为GS的第1层条件属性集，在实验中记为level_1，前两个作为第2层level_2的条件属性集，前3个作为level_3的条件属性集，将4个属性子集结合在一起作为level_4的条件属性集。关于每个数据集的粒结构，每层的属性个数如表6所示。

Table 5 Description of datasets表5 数据集描述

在实验中，每个数据集随机选取4个损失函数矩阵来计算每层的决策阈值。其中，Balance和Contraceptive Method是9×3的损失函数矩阵，Car是12×4的损失函数矩阵，Zoo对应的是21×7的矩阵。然后，根据本文提出的多类分类模型，计算出每层决策后划分到决策类的对象数，具体的实验结构如图1所示。

Table 6 Attributes under each level of granular structure表6 粒结构下每一层的条件属性

图1展示了数据集在每层决策后，决策表中划分到决策类的对象数和没有划分到决策类的对象数之间的变化。从图1中可以看出，每层分类后非确定决策类的对象数逐渐减少。因此，数据集中划分到决策类中对象数逐渐增多。接下来，为了验证算法2比算法1有效，将4个数据集分别在算法1和算法2下进行计算，每组实验进行100次，然后取其平均值作为最终的运行时间，实验结果如图2所示。

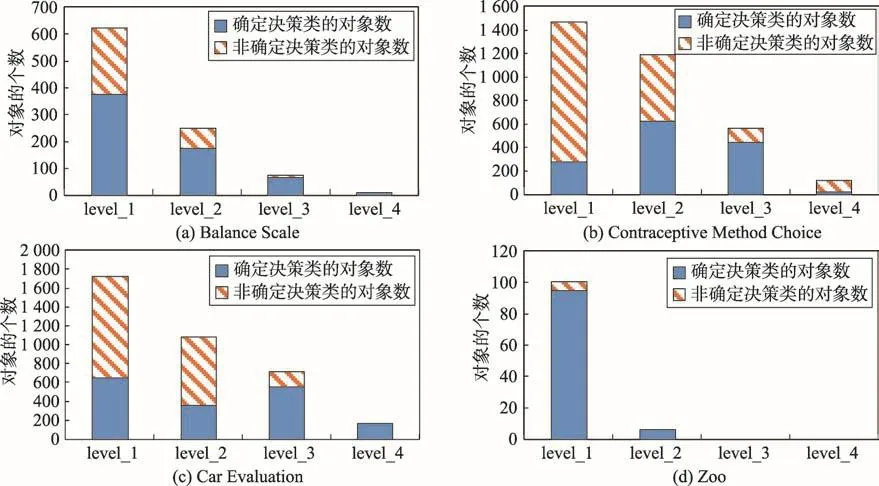
Fig.1 Comparison among the number of objects of determining decision class for 4 datasets图1 4组数据集分别确定决策类的对象数对比

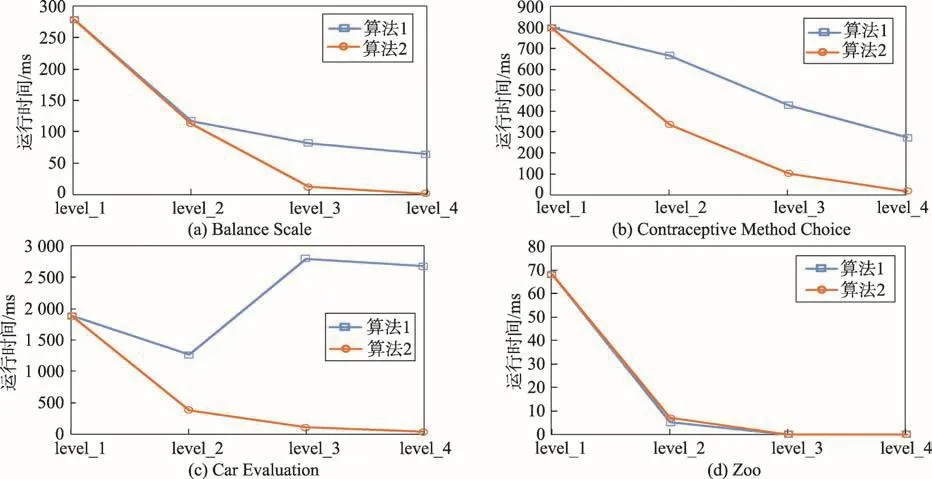
Fig.2 Running time comparison between algorithm 1 and algorithm 2 for 4 datasets图2 4组数据集分别使用算法1和算法2的运行时间对比

图2 是使用增量算法2与非增量算法1去计算多类分类问题的运行时间对比。在多层次粒结构的第一层中，算法2和算法1的计算过程是一样的，因此该层的运行时间是一致的，但是在第二层到第四层中，经过决策过程中增量处理，可以看到算法2的运行时间要比算法1的运行时间少。因此，本文提出的增量算法是有效的。

6 结束语

实际应用中，序贯三支决策是一种有效的动态决策方法去处理多粒度变化问题。本文针对多类分类的决策问题，提出一种基于序贯三支决策的多类分类模型来求解问题。在模型中，利用信息熵来确定对每层决策帮助最大的条件属性，然后构建多层粒结构，从不同粒度层次上进行多类分类。为了减少使用该模型计算决策类的对象数的运行时间开销，提出了增量的方法去计算决策类的对象数。在此基础上，给出了基于序贯三支决策的多类分类增量算法。仿真实验验证了本文所提算法的有效性。在以后的工作中，将进一步研究其他的基于序贯三支决策的多类分类模型。