云计算中基于动态虚拟化电子流密码的安全存储*

任晓莉，杨建卫，李乃乾

宝鸡文理学院，陕西 宝鸡 721016

1 引言

云计算是一种计算范式，用于促进从共享资源池（存储、服务器、网络等）按需随时随地访问网络，它提供了即时更新、更好的资源利用、低成本计算以及更好的存储平台[1-2]。现代社会中，云服务提供商以虚拟化的形式提供服务。虚拟化环境利用虚拟化的服务器、存储、网络、操作系统等创建模型。虚拟化模型VM（virtual model）还提高了灵活性，通过虚拟化，云服务提供商（cloud service provider，CSP）将工作负载部署到其他系统而不是一个系统，以实现更高的性能[3-4]。

在文献中，许多研究者都研究了远距存储数据真实性和完整性问题。例如文献[5]针对远距存储数据真实性和完整性问题，讨论了云模型中数据云中心虚拟化的一些方法。文献[6]提出了一种基于分组密码的VM磁盘安全体系结构，该加密解密方法采用适当的安全性和梅克尔哈希树（Merkle Hash tree,MHT）来保持适当的验证方案，同时采用Merkle一次签名方案实现真实性，但是这种方法存在一些安全问题，如密码分析、冲突攻击。文献[7]介绍了基于经典的MHT和MD5哈希函数的128位加密算法，但这种方法存在一些安全问题，如128位差分密码分析。文献[8]描述了一种基于安全签名方案的最新版本的公共审计方案，以获得适当的真实性，并支持相互认证。但是签名方案在签名验证过程中耗时两步，对于数据中心的动态更新或修改不够及时。文献[9]构造了一个安全短签名方案，该方案具有更好的性能，但是该方案是一种静态方案，通用性不强。文献[10-13]介绍了一种新的动态第三方审计协议（third party audit，TPA），其检查云数据中心用户敏感数据的完整性和真实性。但由于TPA直接参与安全检查，将有可能泄露关键数据。

上述方法大多基于里德-所罗门码率-纠错码等纠错码。本文提出了一种安全的基于流密码的加密/解密方法，以在云数据中心维持对用户敏感数据的适当安全性。为了在VM磁盘之间保持正确的完整性和真实性，引入一个动态版本的DBHT（dynamic B+Hash tree），在没有随机Oracle签名方案的情况下，使用q-SDH（q-strong Diffie-Hellman）安全短签名。

2 基于流密码的加密方法

本章简要介绍基于萨尔萨电子流密码家族成员ChaCha20的加密算法。该流密码算法包含3个基本部分：

（1）密钥流设置阶段

该阶段的基本输入是256位初始密钥以及96位随机数和32位计数器。这些值是通过执行8位小字节整数的级联而形成的。将这些值排列成初始状态矩阵，并在矩阵上应用四分圆函数运算，如下所示。

首先，在新的输入明文的每128位上执行列和对角矩阵的变换，在初始状态矩阵上重复执行20个循环。每个单词更新两次，并执行1/4循环函数。1/4函数的符号表示为四分圆(a,b,c,d)，其中a、b、c、d是ChaCha20的索引，被视为向量。例如，如果1/4轮函数应用于（0,4,8,12）到初始状态矩阵，则1/4循环操作更新用指针符号值进行标记，最后密钥设置阶段产生64个随机字节的输出。

（2）基于流密码的加密阶段

在这个阶段，为了加密密钥，采取256位密钥流，在初始状态矩阵XORD上执行20轮1/4循环函数，并用16个单词明文文件执行。加密过程见算法1所示。图1描述了用ChaCha20算法加密过程。

算法1ChaCha20流密码算法

（3）基于流密码的解密阶段

通过密钥流对密文文本文件进行异或运算，电子流密码的解密操作与加密操作相同。为了保持不同的VM磁盘之间的完整性，使用改进的动态Merkle B+哈希树（dynamic Merkle B+Hash tree，DMBHT）算法进行流密码的解密，具体在下章中进行描述。

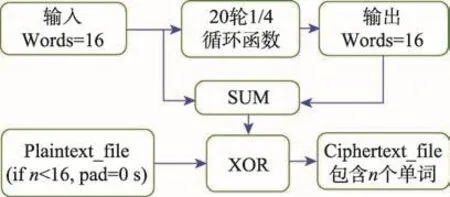
Fig.1 ChaCha20 stream cipher algorithm flow图1 ChaCha20流密码算法流程

3 动态Merkle B+哈希树算法

3.1 算法描述

在现代云计算环境中，客户端更倾向于将其数据存储到云数据中心。云服务提供商（CSP）将该信息以元数据的形式存储在定位区域的一小部分中。为了使用消息摘要MD（message digest），任何客户端或用户可以从分配的部分检索数据。为了执行此过程，使用一种称为DMBHT的方案，本节设计了一种DMBHT的动态改进方案。

首先，对哈希树的叶层哈希值个数进行设置：H(M1),H(M2),…,H(Mn)（SHA-512哈希函数）。这种结构具有O(logn)的最坏情况复杂度。DMBHT的每个叶节点都由left(t)、right(t)和rank(t)三部分构成，即秩表示一个节点上的依赖下降的总数：

式中：

U(t)=h[U(left)||U(right)||U(middle)||ρ(t)||rank(t)]

U(elem)=h(H(M))

为了在客户机和服务器之间保持正确的真实性，在密钥生成方法中生成私钥[Signprvt_key(U(W))]，在DBHT的根节点R上签署了一个不带随机预测的短签名方案，并最终将数据文件连同签名φ、DMHT（dynamic Merkle Hash tree）和U(W)一起部署到云数据中心。图2描绘了算法结构。

DBHT算法描述过程中主要包括以下参数：

（1）Key_generation(λk)→(pub_key,prvt_key)：这一阶段的算法以安全令牌λ为输入，生成一对公钥和私钥。在更新和签名期间使用这些密钥。

Fig.2 DBHT algorithm description图2 DBHT算法描述

（2）Preparation(pub_key,FB,FBtag)→(φ,Signprvt_key(U(W)),DMBHT)：这一阶段的算法通过使用速率φ伪擦除Tornado-z代码生成块标记（flagged block，FB），用于对块中的数据文件进行编码，并在DMBHT(Mi)叶层面形成这些块标签的哈希值，形式为(FBtags)FBtag={H(Mi)}，0≤i≤n。同时，它在DMBHT的非叶节点上生成一组签名φi。最后，它在根节点R上签名作为该步骤的输出。

（3）Challenge_generation(1)→Qr：在该算法的步骤中，客户端生成动态树的叶级数据文件块的每个索引查询集和随机值si∈Zp，并为所有数据文件块标签集定义(ID=id1,id2,…,idk)。最后，客户端向服务器端发送(Qri,si)的计算值作为服务器端的块标签验证步骤。

（5）Verification：在该算法中，客户端运行验证功能，验证VM磁盘数据的真实性。在验证阶段，客户端在根节点R上生成Signprvt_key(U(W))值。为实现验证有效性，可通过检查存储在叶级上的VM磁盘数据e(δ,δ)获得：

（6）Updation Process：假设将DMHT的叶级存储在VM磁盘的kth块中，K的任何用户都希望从M到M!更新数据，用户请求用UPDATE_REQUEST()进行更新：

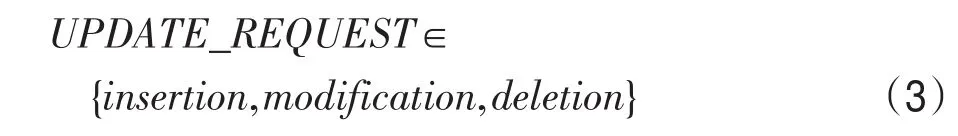
现服务器有两个验证值{Prold,Prnew}，并将这些值发送给客户端。在从服务器端接收证明值时，客户端通过执行UPDATE_VERIFICATION()函数验证这些证明，并生成输出(True,False)。DBHT的插入、更新和删除操作如图3所示。

3.2 签名方案

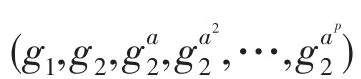
（1）退化：e(P,Q)≠1。

最后，签名方案具有安全性参数(G,GT,e,p,g,Zp[+1])，其中Zp[+1]可定义为：

签名方案过程具体如下：

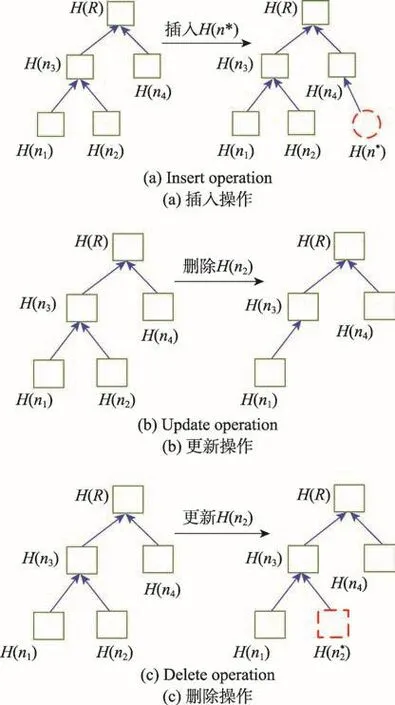
Fig.3 Insert,update and delete operations in DBHT图3 DBHT中的插入、更新和删除操作

3.3 VM磁盘数据安全性和完整性

根据所提方法，将加密敏感数据存储在VM的磁盘中，并创建DBHT叶级VM磁盘的大散列值。不可伪造签名方案用于在所有非叶节点上进行签名，并实现在DBHT根上签名(δ)。此过程表示如下：

（1）每当用户/客户端想要在数据中心上传数据时，则使用电子流密码ChaCha20对数据进行加密。

（2）找到VM磁盘的散列值，并将大量散列值安排到DBHT中。

（3）将DBHT连同签名一起发送给服务器。

（4）在下载时，首先检查VM磁盘的完整性和真实性，然后通过VMM（virtual machine monitor）级别存储的初始矢量以小的结尾格式存储在VM磁盘上解密数据。

图4中描述了从云数据中心下载数据的完整性验证过程。

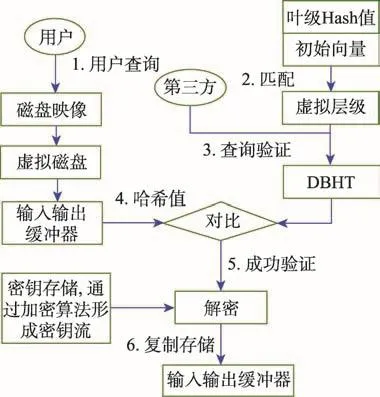
Fig.4 Cloud data center download data integrity verification图4 云数据中心下载数据完整性验证

4 安全性分析

4.1 流密码的安全性分析

在所提算法构造中，提出了利用块函数生成的256位密钥流{0,1}256×{0,1}128→{0,1}512。这个函数将16字节作为输入，64字节作为输出。选择明文攻击下的不可区分性安全问题：

（1）如果对手能够区分由初始加密E0与相同长度的随机比特串生成的(C,T)，则对手赢得游戏。因此，对手获胜的可能性是：

（2）如果对手可通过改变输出元组(N,A,C,T)来伪造密文Dk(N,A,C,T)=(N,A,P)≠⊥，其中(N,A,C,T)可能不是由加密和解密Oracle输出⊥所设置的正确密文，其是无效的，那么它将显示对手可以改变CT值。对手获胜的可能性是：

4.2 基于DBHT的安全性分析

定理1假设在n-块文件FB上的重复证明器表现良好，且它是∈可容许的。令E=1/#Block+(∂Y)l/(Y-C+1)C，假设(∈-E)是正的和不可忽略的，在欺骗O(Y/∈-∂)的时间内，可以在时间 O(Y2+(1+∈Y2)(Y)/(∈-E)内恢复编码的文件块。

证明提取器在每个点的知识是一个子空间D，由一个t×n矩阵A表示的行降级。假设有助于提取器知识的查询响应对：

同时，VM=W，其中V是t×n矩阵的行是{qi}，W是t×s矩阵，其行是。行降阶矩阵A与V有关的A=UV，其中U是t×t矩阵，其非高斯行列式应用于高斯消去法计算。

（1）提取器的知识最初是空的，即K=0。

（2）提取器重复以下行为直到#freeK≥ρn。

提取器选择在B上运行的随机查询Q。假设B选择回答给出答案 (μ,…,μs)。令Q超过指数I∈[1,n]，并用矢量符号表示为q。现在把Q分为三个步骤：（1）q∉K；（2）q∈K，但是I!⊂freeK；（3）I⊂freeK。

对于查询，提取器将Q添加到其知识K，并获得如下新知识D1。它通过获得对应于W的响应的V1和行来添加与查询V对应的行。并获得具有A1=U1V1的W1变换矩阵U和U1。显然，如果一维K等于n，则类型1查询增加维度K，则freeK=n≤ρm。查询最多构成查询空间的一个(1/#B)部分。因为：

由此定理1得证。

定理2给定编码文件FB的Y块的分数部分，可以完全可忽略的概率检索完整原始文件FB。

证明在所提算法模型中，使用速率伪删除码（Tornado-z）来编码DMBHT的叶级上的块标签（FB）。根据Tornado-z码的性质(k=d+h)，客户端/用户能够从小部分（冗余块）检索完整文件块。具有速率伪擦除码的Tornado-z码以原始数据(d)的形式与冗余数据(h)结合，即r=d+h。任何客户端/用户都可很容易地从足够的部分或多个块分组中获得原始消息。

4.3 签名方案的安全性分析

定理3假设(G1,G2)中的签名方案(q,T!,∈!)，则在自适应选择消息攻击下签名模型是(T,qs,∈)，其信息伪造攻击为qs=q，∈≥2t!+qs,p≈2∈!和T≤T!-θ(q2t)，其中t是G1、G2和Zp中幂次运算的最大时间。

证明假设伪造者将打破签名方案(T,qs,t)。现在，生成与A交互算法B，并尝试在时间T!中基于优势∈!解决q-SDH问题。算法B提供在(G1,G2)中q-SDH问题的随机细节(g1,e1,e2,…,eq,g2,F)，其中e1=对于v∈Zp/{-v}，算法B的目的是生成一对利用这个定理，给出所提算法对明文攻击的安全性。

5 实验分析

在对云计算中基于动态虚拟化电子流密码安全存储过程进行验证过程中，采用实验硬件：处理器是i7-6400K，内存是4 GB ddr4 2 400 KB，实验平台选取Matlab2013b。对比算法选取两种已有的云存储安全算法，分别见文献[14-15]所示。其中，文献[14]采取的是密钥配对检测方法，文献[15]采取的是数据的远程密钥审核策略。

5.1 计算复杂度分析

（1）检测概率

假定实验过程中存储文件的大小是1 GB、10 GB、100 GB和1 000 GB四种不同规模。设置检测概率变化区间是P=90%、95%和99%三种变化区间。通过实验分析对所提算法在响应和验证两个算法阶段的计算成本指标随着存储文件大小变化情况见图5所示。

Fig.5 Experimental comparison of computation cost(detection probability)图5 计算成本实验对比（检测概率）

按照图5所示计算成本实验对比结果可知，检测概率参数对计算成本指标具有直接的影响关系，检测概率越高需要算法的计算复杂度越大。原因在于检测概率参数越大需选取的存储文件的质询消息数量越大，这会造成算法的计算过程趋缓，产生更多的计算步骤。对于不同的文件规模，在算法的响应过程中，其计算复杂度与存储文件的大小关系不大，响应计算复杂度曲线呈现出相对平稳的变化趋势。而在算法的验证过程中，对于不同的文件规模，验证计算过程的复杂度曲线变化较为明显，这表明在这个过程中存储文件大小对于算法的计算复杂度影响较大。

（2）q-SDH安全短签名长度

假定实验过程中存储文件大小是1 GB、10 GB、100 GB和1 000 GB四种不同规模。设置q-SDH安全短签名长度为SL=16 bit、32 bit、64 bit、128 bit和256 bit。通过实验分析所提算法数据传输成本指标随着存储文件大小变化情况见图6所示。

按照图6所示计算成本实验对比结果可知，对于设定的1～10 GB变化区间的文件大小，因为本文实验过程中配置的硬件资源较高，且均未超出数据传输带宽上限，因此q-SDH安全短签名长度这个指标对于数据传输成本指标的影响较小，基本呈现出接近于0的传输成本。而对于10～1 000 GB文件大小区间，q-SDH安全短签名长度这个指标对于数据传输成本影响较大，q-SDH安全短签名长度指标越大，算法的数据传输成本越高。

Fig.6 Experimental comparison of data transmission cost(q-SDH short signature length)图6 数据传输成本实验对比（q-SDH短签名长度）

（3）D&CTs数据结构影响

动态数据更新过程中，D&CTs数据结构对于数据更新具有重要的作用。为降低算法的计算复杂度，需要针对选取的存储文件数据块m对数据结构参数k的值进行设置。实验过程中，首先定义实验场景对D&CTs数据结构的动态更新影响情况进行分析：更新外包文件f的大小变化区间是1～100 GB，数据块的数量变化区间是125 000～1 125 000。存储文件数据块分解数量设定为10～353。插入、更新和删除操作的总数上限设定为2 000。对数据块位置进行随机选取，并且在实验分析过程中保持相对的恒定。实验结果见图7所示。

Fig.7 Experimental comparison of computation cost(D&CTs data structure)图7 计算成本实验对比（D&CTs数据结构）

按照图5所示计算成本实验对比结果可知，数据块数量的增加会造成云存储过程中安全性检验过程的计算复杂度增加。总体来看，相对最佳数据块数量是在kopt=354时的数据块数量125 000。同时，根据图7所示实验结果可知，更新请求的增加会导致算法的计算成本增加，两者之间存在直接的关联。例如，若参数k的取值从k=100变化到k=354过程中，对文件大小为1 GB的1 000个数据块进行安全性验证的计算复杂度大约是0.140～0.218 s，呈现出增加趋势。

图8所示为在选取的大型存储文件上，执行存储更新100次，所需要的算法计算成本对比实验结果。实验过程中，参数的具体设置为P=90%，数据块规模为16 KB，数据的存储损坏比例是0.02%，q-SDH安全短签名长度SL=256 bit。对比算法仍然选择上述文献[14-15]两种算法。

根据图8所示算法对比实验结果可知，随着存储文件大小的增加，本文算法在云存储节点实现再平衡所需的计算时间变化幅度不大，主要原因是本文算法是一种动态计算方法，而对比算法随着存储文件大小的增加，云存储节点实现再平衡所需的计算时间呈现出增加趋势。文献[14]算法是静态的云存储数据审计方法，云存储文件在10～60 MB区间内变化时，算法大约产生380 ms的计算复杂度，而文献[15]大约可产生405 ms的计算复杂度，上述实验结果体现了本文算法的动态计算效率。

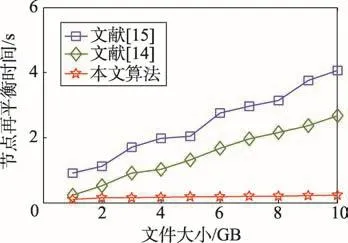
Fig.8 Algorithms contrast experiments图8 算法对比实验

5.2 成功检索实验对比

为证明所提算法鲁棒性，设定有关模型参数取值：节点数n=1 024，数据块大小k=256，测试样本阈值u=1～35，p为实验中用到的素数。对比算法是文献[4-5]以及文献[6]，数据损坏率指标选择ε=1%、5%、10%及20%，四种算法的成功率对比实验结果如图9所示。

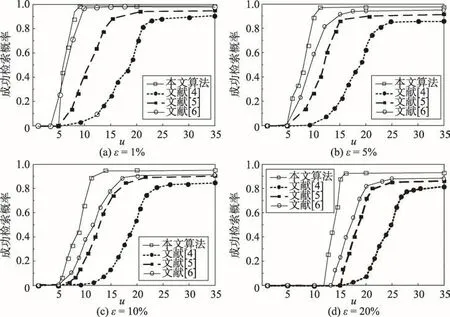
Fig.9 Comparisons of successful retrieval probabilities图9 成功检索概率对比

根据图9所示结果，如果数据损坏率指标增大，则对于相同的成功率指标设定结果，本文需要进行的服务器查询数量最小，表明本文算法在检索成功率指标上具有更加优异的性能表现。文献[5]计算得到的成功率指标结果在集中算法中最差，但是文献[6]相对于本文算法和文献[4]算法，在数据损坏率指标增大时的性能降低幅度最快，逐渐接近于文献[5]算法性能结果。

6 结束语

本文提出了一种云计算中基于电子流密码的安全动态更新存储策略。主要贡献是提出一种新的Merkle哈希散列B+树的动态版本，采用Q-SDH安全短签名，在DBHT的叶级上采用有效的码率作为伪删除码（Tornado-z码），可有效保持虚拟机磁盘之间的完整性和真实性。

上述算法主要是针对单服务器云存储情形进行设计的，但是单服务器云存储存在的问题是对数据损坏问题缺乏有效的恢复措施。因为其没有数据的备份功能，所以在今后的工作中，主要是将算法方案进行分布式云服务器的适应性设计，提高数据损坏恢复的鲁棒性。