云科学工作流截止期限约束代价优化调度算法*

陈彦橦，裴树军，苗 辉

哈尔滨理工大学 计算机科学与技术学院，哈尔滨 150080

1 引言

现代科学在天文学、地球科学、生物信息学等不同研究领域中运行日益繁杂的大规模科学应用，以模拟和分析现实世界的活动，而科学工作流已被证实是建模和管理这些复杂问题的最有效手段[1]。科学工作流通常由一组通过控制和数据依赖链接的粗粒度并行计算任务组成。随着数据生产速度的提升和计算系统的日益复杂化，科学工作流越来越体现为大数据形式，如计算密集型和数据密集型[2]。科学家通常将科学工作流部署在传统的分布式执行环境，如集群和网格等平台上，然而系统的建立所付出的代价是非常高昂的，且资源的扩展性较差[3]。近年来随着云计算技术的发展，其在性能和成本方面为科学工作流提供了相当好的解决方案，云以虚拟机（virtual machines，VM）的形式为用户提供计算资源，与传统的分布式执行环境相比，具有无限的计算和存储资源、资源按需提供以及允许用户弹性地获取和释放资源等优点。虽然云环境有很多优势，但仍然存在某些需要通过预期调度策略解决的特定问题，例如虚拟机实例采集延迟、虚拟机资源的异构性及动态按需提供等问题。

工作流的调度主要包含两个层次：一是任务与虚拟机实例之间的映射；二是单个虚拟机上任务的顺序执行。调度算法的众多性能指标中，用户最关心的两个指标为工作流的完成时间和执行代价。分布式资源上的工作流时间代价优化调度是一个NP-hard问题，对于这类问题，利用基于启发式和元启发式的调度算法能够取得近似最优解[4]。

相关研究中，文献[5-7]提出基于逆向分层的截止期限约束费用优化算法TCDBL（temporal consistency based deadline bottom level）和 PBCO（path balance based cost optimization），将截止期限分解到各层，使费用优化问题由全局转化到局部。在此基础上提出CACO（communication aware cost optimization）算法，采用动态规划收集任务与虚拟机匹配时产生的时间碎片，改善费用优化效果，但并未为任务设定优先级来找到最佳调度顺序。文献[8-9]提出了基于部分关键路径的调度算法IC-PCP（IaaS cloud partial critical paths）和CPC（critical path cut），将局部关键路径中的任务都安排在同一个费用最低的VM实例上，避免了任务间的通信成本，但多条部分关键路径分配到不同VM上时，由于任务间的数据传输将导致较低的任务调度成功率。文献[10-11]提出自适应调度算法 MOEA（multi-objective evolutionary algorithms）和UQMM（uncertainty-based quality of service Min-Min），用于在异构多云环境中实现用户定义约束的任务调度，使算法具有更高的适用性。

近年来，很多学者侧重于利用智能搜索算法解决调度问题。文献[12-13]提出基于蚁群的元启发式算法，放宽截止期限引导搜索朝着约束方向优化。文献[14]提出基于粒子群的最优调度算法，利用关键路径进行粒子初始化和搜索阶段的筛选处理，提高搜索结果的精度和降低搜索的计算时间。文献[15]提出一种模拟退火遗传改进算法SA（simulated annealing），将模拟退火算法与遗传算法相结合，用以解决工作流的多目标优化问题。虽然这些方法都具有良好的表现，但与其他基于启发式的方法相比，智能搜索算法在初始化阶段耗时过多。

针对异构云环境下科学工作流截止时间约束的代价优化调度问题，本文提出了基于约束关键路径的代价优化算法（cost-optimized scheduling algorithm based on constrained critical path，CSACCP）。算法分为两个阶段：第一阶段设定任务的向上权值，根据权值将工作流分解为约束关键路径（constrained critical path，CCP）集合。第二阶段在满足截止期限约束的条件下，通过最小费用增长代价和及时完成的VM选择策略，结合首次适应插入算法，实现每条约束关键路径与最优VM的匹配。

2 系统模型

2.1 科学工作流模型

科学工作流通常用有向无环图（directed acyclic graph，DAG）进行描述，表示为G=(T,E)，其中T={t1,t2,…,tn}表示一个含有n个任务节点的有限集，E={eij|ti,tj∈T}表示任务之间数据依赖关系的有限边集。每条数据依赖边eij=(ti,tj)代表任务ti和任务tj之间的数据控制依赖关系，其中任务ti称为tj的直接前驱，任务tj是ti的直接后继。用pred(ti)表示任务ti的直接前驱集合，succ(ti)表示任务ti的直接后继集合。|eij|表示两个任务之间的数据传输量。

在一个给定的DAG工作流中，一个不存在任何前驱任务的任务称为入口任务tentry，一个不存在任何后继任务的任务称为出口任务texit。若一个DAG中存在多个入口任务或多个出口任务，则需要增加一个虚拟任务（计算和通信开销都为0）来保证DAG在进行调度时有唯一的入口任务和出口任务。

一个拥有11个任务的简单工作流如图1所示，每个节点代表一个任务，边上的权值代表两个任务之间的数据传输量。

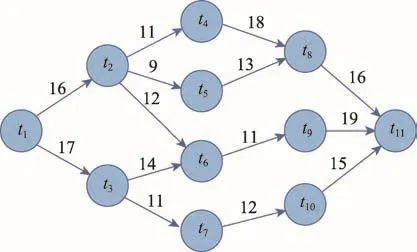
Fig.1 Sample workflow图1 工作流示例

2.2 云资源模型

云资源以m种异构的VM形式提供VMSET={VM1,VM2,…,VMm}，每个VM类型，在其CPU性能、内存容量和资源定价等方面都拥有自身配置。资源定价基于Amazon EC2中按需提供的定价模型，用户根据VM租赁时间间隔（timeinterval）的数量付费。同时当VM租用时，需要一个引导时间对VM进行初始化以便用户使用，用户可根据需要部署相应的软件资源。

由于云服务商提供独立于VM生存期的存储服务，例如EBS（elastic block store），因此当输入数据文件传输到相应的存储资源时，要执行子任务的VM不需要处于活动状态。此外由于用于存储输入输出数据的存储资源所需的成本与调度算法无关，因此在此模型中未考虑。假设所有计算和存储服务都位于同一数据中心或区域，计算服务之间的平均带宽基本相同，用β表示。当两个具有数据依赖关系的任务所选的VM实例不同时就会产生通信开销，则此时两任务之间通信开销如式（1）所示：

表1给出了实验中使用的Amazon EC2所提供的5种VM资源类型的相关参数，其中一个ECU单元相当于1 GHz Xeon CPU的性能。

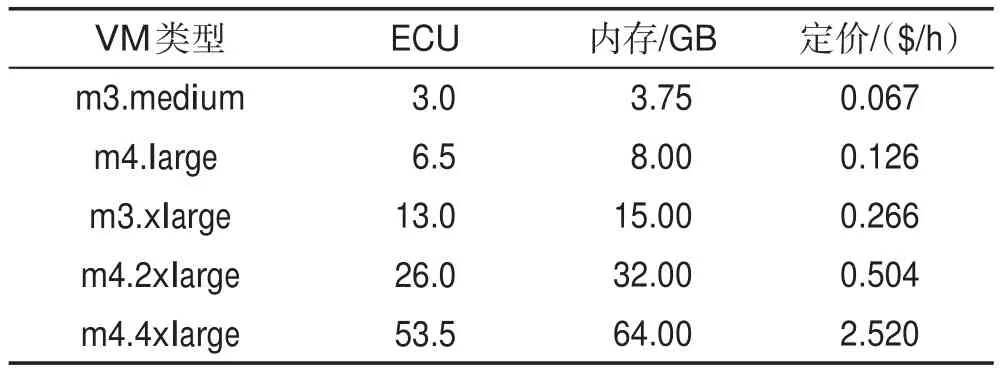
Table 1 Types of VM表1 VM类型

将VMSET中每个VMk定义为一个二元组(EXT(ti,VMk),Cost(VMk))，其中EXT(ti,VMk)表示任务ti在资源类型为VMk上的预期执行时间，如式（2）所示，Cost(VMk)表示单位时间租赁成本。

其中，size(ti)表示任务ti的大小，以浮点计算的运行次数度量；FPC(VMk)表示VMk的计算能力，以每秒进行的浮点运行次数度量。

2.3 计算平台模型

本文使用与文献[16]中相似的计算平台模型，如图2所示。用户提交工作流及相关的服务质量（quality of service，QoS）要求，例如截止时间期限和资源需求到工作流管理系统。工作流管理系统由三个主要模块组成：资源调配模块、工作流调度模块和执行管理器。资源调配模块分析工作流结构以预估所需资源量，动态地向云服务商申请资源，并在租赁期结束时释放资源。工作流程调度模块与执行管理器协调，完成工作流任务与资源之间的映射，并由资源管理器执行。

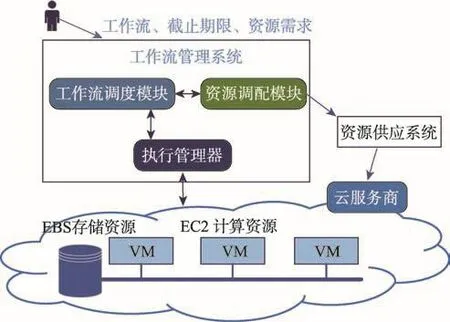
Fig.2 Scheduling system model图2 调度系统模型

工作流管理系统维护一个资源池Active_VMs信息列表，资源池信息列表中存储每个申请到的资源实例的类型、开始时间和结束时间，如式（3）所示：

2.4 调度目标

工作流调度目标定义如下：

为工作流G规划一个时间表S，在总执行时间makespan不超过工作流截止期限D的条件下，最小化运行工作流的执行代价CostTotal，如式（4）所示：

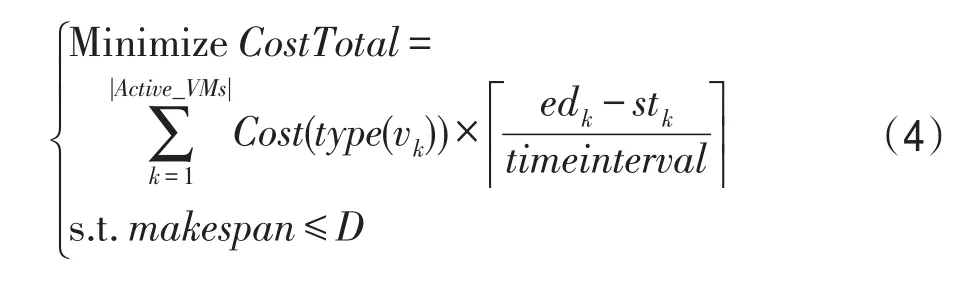
3 CSACCP算法设计

本章首先介绍与算法有关的基本定义，然后设计CSACCP调度算法。算法首先调用Gen_CCPSET将工作流分解成CCP集合，然后通过CheapestMap算法实现每条CCP与最优VM的匹配，以期在异构云环境中在满足用户截止期限的约束下尽可能减少执行代价。

3.1 基本定义

定义1MXT(ti)表示任务ti的最小执行时间，定义为其在VMSET中所有资源类型上最小执行时间，其计算公式如下：

定义2EST(ti)表示任务ti的最早开始时间，定义为其所有直接前驱被安排在执行时间最小的VM上，并且所有所需的依赖数据都已传递到ti。其计算公式如下：

定义3EFT(ti)表示任务ti的最早完成时间，定义如下：

定义4MEXT_G表示工作流最早完成时间，即出口任务的最早完成时间，计算公式如下：

定义5XFT(ti)表示任务ti被调度到VM实例为vq上的预期完成时间，计算公式如下：

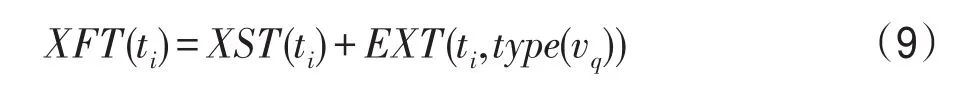
定义6XST(ti)表示任务ti被调度到VM实例为vq上的预期可开始时间，只有在所有直接前驱执行完毕且依赖数据传输到vq时才可开始，计算公式如下：

定义7XIDT(vq)表示VM实例vq的预期空闲时间，其中tp为安排调度到vq上的最后一个任务，计算公式如下：

定义8XET(ti,VMk)表示从任务ti之后开始的关键路径在VM类型为VMk上的执行总时间，计算公式如下：

3.2 CSACCP算法

3.2.1 Gen_CCPSET算法生成CCP

通常关键路径是指工作流任务图中从入口节点到出口节点的最长路径。路径的长度为节点的执行时间的平均值和沿该路径的通信开销的总和。当关键路径上的任务首先被调度时，将产生有效的调度，但是关键路径上的所有任务并非全都准备就绪。所有直接前驱已经为其调度处理的任务被称为准备就绪任务。只包含准备就绪任务的一组任务构成了一条约束关键路径CCP。每个CCP可以根据其任务的完成时间分配一个VM实例，将减少依赖数据传输时间。

HEFT（heterogeneous earliest-finish-time）[17]中将任务ti的向上权值rank定义为任务ti至texit的关键路径长度，并根据rank的大小决定任务执行的优先级。从出口任务开始向上迭代计算每个任务的rank值，计算公式如式（13）所示：

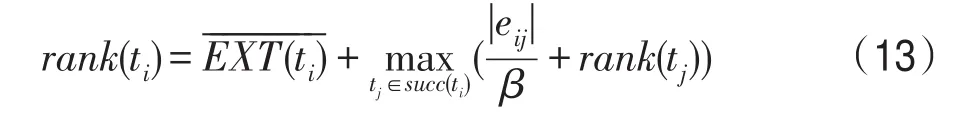
考虑到出度高的任务若没有及时执行会影响整个工作流的执行时间，CSACCP算法将向上权值进行改进，计算公式定义如下：

ranku与HEFT中的向上权值的差异在于聚合了任务直接后继的通信时间，任务的出度越高优先级越高。

算法Gen_CCPSET用于生成CCP集合。首先从降序排列的权值集合中选取最大值任务，查找到其入度为1且权值最大的子任务，继续向下寻找直到不存在入度为1的子任务，生成一条CCP。从权值任务集合中去除CCP任务，并在边集合中去除CCP相关有向边，重复上一步直到集合为空。算法描述如下：

算法1Gen_CCPSET(G=(T,E))

图1中简单工作流每个任务在三种VM类型上的执行时间及计算所得向上权值如表2所示。

Table 2 Upward rank of workflow表2 工作流向上权值

则经过Gen_CCPSET之后生成的CCPSET为：

CCPSET={{t1,t2},{t3,t6,t9},{t5},{t4,t8},{t7,t10,t11}}

3.2.2 CheapestMap算法

CheapestMap算法接收CCPi及资源集合VMs作为输入，并返回其最便宜的适用VM实例cheapestvm。

尽管最便宜的VM实例可能在其最晚完成时间之前完成任务，但它可能不是最佳选择。这是因为任务选择最便宜的VM实例，而不考虑其对后继任务的影响，可能会强制后继任务在更快的VM上执行，从而增加总体成本。因此，本文采用及时完成策略，将最便宜的适用VM实例定义为，在单个VM实例vk上，调度执行此CCPi及从其尾任务ti之后开始的关键路径(最长路径)，在满足截止期限D的条件下使得费用增长代价mincost最小。

由于每个任务必须等待其直接前驱的依赖数据，因此在调度任务之间可能会形成空闲时隙。如果空闲时隙过多，则会产生资源浪费。因此为了提高资源的利用率同时进一步降低执行代价，算法首先考虑对空闲时隙的利用，采用首次适应（first fit）的回填策略，在满足截止期限的前提下，将CCPi插入最合适的空闲时隙，此时最小费用增长代价mincost为0。

对于资源集合VMs中每个虚拟机实例vk，算法由CCPi中每个任务在vk上的XFT(tj)和XST(tj)来计算CCPi的预期结束时间XFTCCP(CCPi)和预期开始时间XSTCCP(CCPi)以及预期执行时间XETCCP(CCPi)，计算公式如下：

若其满足工作流截止期限D，则计算vk的费用增长代价，最终返回最便宜的虚拟机实例cheapestvm。算法描述如下：

算法2CheapestMap(CCPi,VMs)

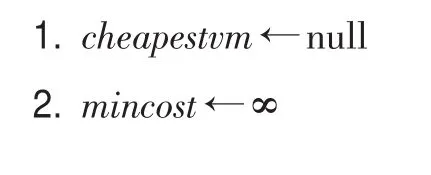
3.2.3 CSACCP算法

为了适应VM采集延迟launchdelay，算法将输入预期的VM采集时间并相应地作出供应决策。由于VM终止延迟不会对工作流程的截止时间限制产生不利影响，因此本算法不考虑终止延迟。

算法首先评估MEXT_G并将其与用户指定的截止期限D进行比较，如果D大于MEXT_G，算法会继续寻找适当的调度时间表，否则会提示用户修改截止期限D。一旦确定了用户指定的截止期限的可实现性，算法调用Gen_CCPSET生成约束关键路径集合CCPSET，再对集合中每条约束关键路径调用CheapestMap，选取最便宜的VM实例进行匹配。

由于活动资源池Active_VMs并不一定满足所需，则将VMSET中每种虚拟机类型新实例集合New_VMs与其合并形成备选资源集合VMs用于选取最便宜的虚拟机实例。若最终选取的实例属于Active_VMs，将其调度到该实例上，并更新活动资源池状态；若属于New_VMs，考虑虚拟机实例采集延迟，在XSTCP(CCPi)-launchdelay时刻新建虚拟机实例，将其调度到新建虚拟机实例上并更新资源池状态信息。算法描述如下：

算法3CSACCP

3.3 时间复杂度分析

为计算时间复杂度，假设工作流G=(T,E)由n个任务组成，数据依赖边的最大数量为n(n-1)/2，云服务商提供m种异构的VM资源。CSACCP首先计算MEXT_G，判断用户定义截止期限的合理性，其时间复杂度为O(n2)。一旦确定用户定义的截止期限是合理的，算法计算XET矩阵，为后续VM与CCP的匹配做准备，其时间复杂度为O(n2m)。接下来算法通过调用Gen_CCPSET算法生成约束关键路径集合，由于需要计算任务的向上权值，其时间复杂度为O(n2m)。最后CSACCP算法为CCPSET中每条CCP调用时间复杂度为O(n2m)的CheapestMap算法进行虚拟机的匹配，考虑所有依赖性的时间复杂度为O(n3m)。此外由于云服务商提供的VM类型的数量是恒定的并且小到足以忽略，因此CSACCP算法的时间复杂度为O(n2+n2m+n3m)=O(n3)。

4 实验结果及分析

4.1 实验设置

工作流采用Juve等人[1]研究的4种不同科学领域中的工作流结构作为测试源，包括天文学领域的Montage、地震科学领域的Cybershake、重力物理学领域的LIGO和生物基因学领域的Epigenomics。每种工作流的大致结构如图3所示，这些工作流具有不同的组成和结构特性。为了便于评估工作流算法，Bharathi等人[18]开发了一个Pegasus工作流生成器来生成类似于真实科学工作流的人工合成工作流，将诸如任务列表、任务之间的依赖关系、计算时间等信息存储在XML格式的文件中。选取3种大小的工作流进行了测试：小型（约100个任务）、中型（约300个任务）和大型（约1 000个任务）。由于实验结果相似，则结果图表中只显示大型工作流的实验结果。为了对所提出工作流调度算法进行评估，本节利用仿真工具CloudSim[19]对由Pegasus生成的不同的工作流进行仿真测试。

Fig.3 Four workflow structures used in experiment图3 实验中所用4种工作流结构

假设云服务提供商提供5种不同类型的VM。虚拟机实例配置及处理能力基于Amazon EC2，参数如表1所示，不同虚拟机之间的平均带宽设置为20 Mb/s，VM的采集延迟设置为97 s[20]。

每个工作流需要一个对应的截止期限来评估所提出的算法，太短的截止期限会导致大部分工作流无法及时完成，如果截止日期非常宽松，则有足够的时间以较低费用完成工作流的执行。为了设定截止期限，通过式（18）将截止时间分布于严格、适度与宽松之间。

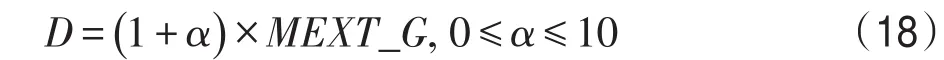
截止期限因子α从1开始考虑非常严格的截止期限（通常接近最快执行时间），最高为10的非常宽松的期限，且步长为1。

4.2 对比算法

为了验证CSACCP调度算法的有效性，选择ICPCP[8]和RCT（robustness cost time）[21]作对比算法，在考虑所有依赖性的前提下，3种算法时间复杂度均为O(n3)。

IC-PCP算法是针对本问题最常引用的算法之一。算法分为截止期限分布和规划调度两个阶段，算法将用户定义的截止期限分布在所有任务上，起始于将关键路径上的关键任务在满足截止期限的前提下，安排在最便宜的VM上执行以消除通信代价，然后通过递归计算关键路径上未被调度的后续任务的关键路径，重复以上步骤直到所有任务调度完成。但是IC-PCP算法并未考虑到VM的采集延迟。

文献[21]中提出了一种健壮性的工作流调度算法RCT，该算法考虑了云环境中资源采集延迟，依据成本和时间的权重设定目标函数。基于部分关键路径PCP（partial critical path），由健壮性类型定义的一定量的松弛时间被添加到PCP执行时间，每个PCP都有可行解集合FS（feasible solution），从FS中选择适当的VM实例。

4.3 实验结果分析

4.3.1 性能指标

为了评估被测算法，选择使用以下性能指标：任务调度成功率SR（success rate）和标准化执行成本NEC（normalized execute cost）。

每个算法的任务调度成功率SR，计算为成功达到预定期限的模拟运行次数nk与模拟运行总次数ntotal之间的比率，定义为：

因为存在多种不同性质的科学工作流，所以需要一种标准化方法统一定义执行成本。本文首先考虑了在最后期限内失败的成本，因此标准化执行成本NEC定义为：

其中，CostTotal是满足期限工作流的成本，已在式（4）中定义。MinCost为利用贪心策略将所有任务分配到最便宜的VM实例中的执行成本。

4.3.2 算法执行时间

表3具体介绍3种调度算法针对不同类型的4种工作流的平均执行时间。考虑所有任务依赖性的前提下，时间复杂度均为O(n3)，结果表明3种算法的执行时间相差不大。值得注意的是，在LIGO工作流中，CSACCP算法的执行时间相对其他算法有所降低。这是受工作流结构的影响，由于CSACCP算法执行时间主要消耗在为CCP查找最便宜的VM上，CSACCP将LIGO工作流分解为多个结构相似且执行时间较短的约束关键路径，使大量的CCP更容易满足首次适应的插入策略，减少了每条CCP在查找最便宜的VM时的计算时间。因此执行时间有所降低，在大型工作流中较为明显。

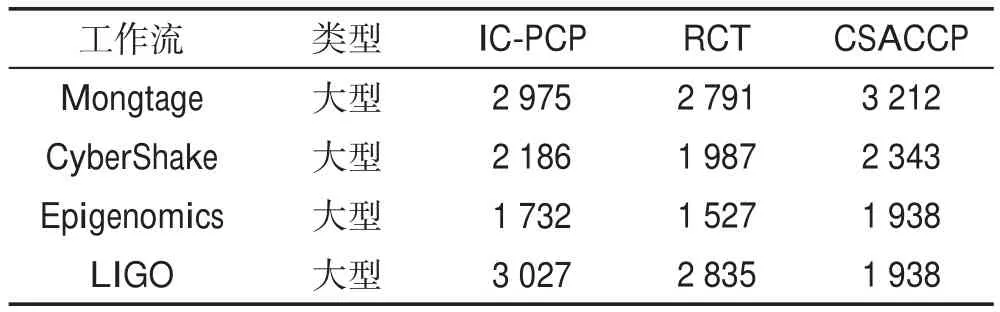
Table 3 Average running time of 3 scheduling algorithms表3 3种调度算法平均执行时间 ms

4.3.3 调度成功率

评估每种工作流在不同截止期限因子的情况下任务调度成功率，结果如图4所示。

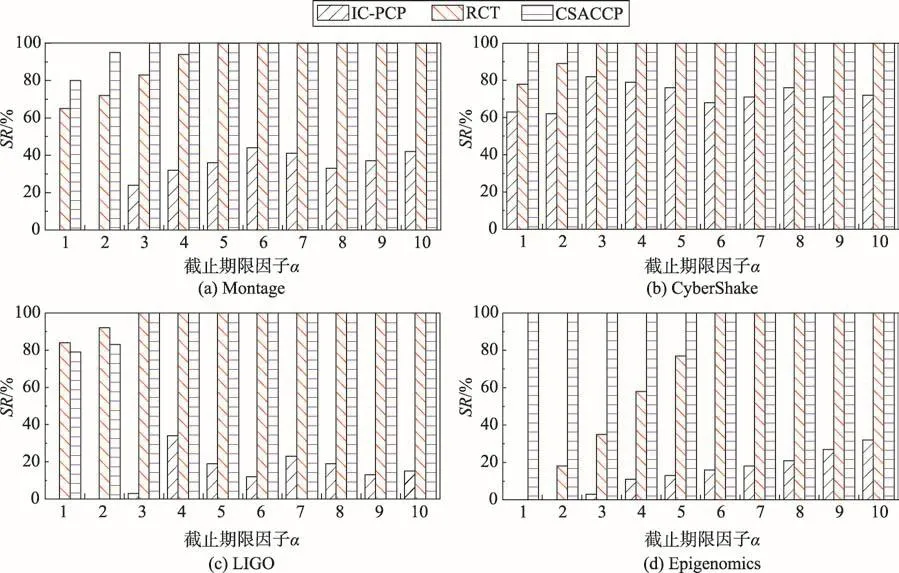
Fig.4 Scheduling success rate图4 调度成功率

图4显示了截止期限因子α从1增加到10，每种算法的调度成功率SR。较低的成功率表明算法无法找到符合截止期限的完成时间。可以观察到IC-PCP在α为1和2时，在大多数情况下都无法找到满足截止期限的调度策略。这是因为算法首先遍历工作流，在忽略任务间通信开销的前提下，将整条关键路径分配到一个最便宜的VM上。在后续的迭代选取剩余部分关键路径并为其分配VM时，由于分配到不同VM上的任务间需要通信开销，这将导致在严格截止期限下，已分配的关键路径无法在预期的时间内完成，因此整体表现较差。

除Epigenomics之外，RCT和CSACCP在适度和宽松的截止期限内没有明显差异，但是CSACCP在严格的截止期限内比RCT有更好的表现。这是因为RCT将成本及执行时间设定目标函数，成本的优先级高于执行时间，这将导致在严格的截止期限内的表现不如CSACCP。尤其具有高并行度局部关键路径的工作流Epigenomics，每条局部关键路径都具有较长的执行时间。RCT优先考虑对执行成本的影响，在满足最小费用增长的前提下，将多条局部关键路径分配到一个VM上，忽视了对截止期限的影响，因此在严格的截止期限内无法找到合适的调度策略。而CSACCP设定了任务的向上权值，优先调度对工作流执行影响较大的任务，并且降低任务间通信代价，每次在为CCP分配VM时，综合考虑对费用增长代价和截止期限的影响，因此有较高的调度成功率，在严格的截止期限内成功率均高于60%。

4.3.4 标准化执行成本

图5中的实验结果表明，工作流调度的成本通常随着截止期限因子的增加而减少。由于NEC受调度成功率SR的影响，若无法找到合适的调度策略会引起数据值的缺失。在大多数情况下，CSACCP和RCT算法的性能优于IC-PCP算法，在所有工作流的截止期限内实现了最低的总执行成本。如所有启发式算法一样，有些方面表现并不是最优，但是这些方面都是少数。例如在Cybershake中，当α＜3时，RCT表现出更少的执行成本，但在此阶段CSACCP比RCT有更高的调度成功率，且随着截止期限因子的增加，CSACCP有着更好的表现。

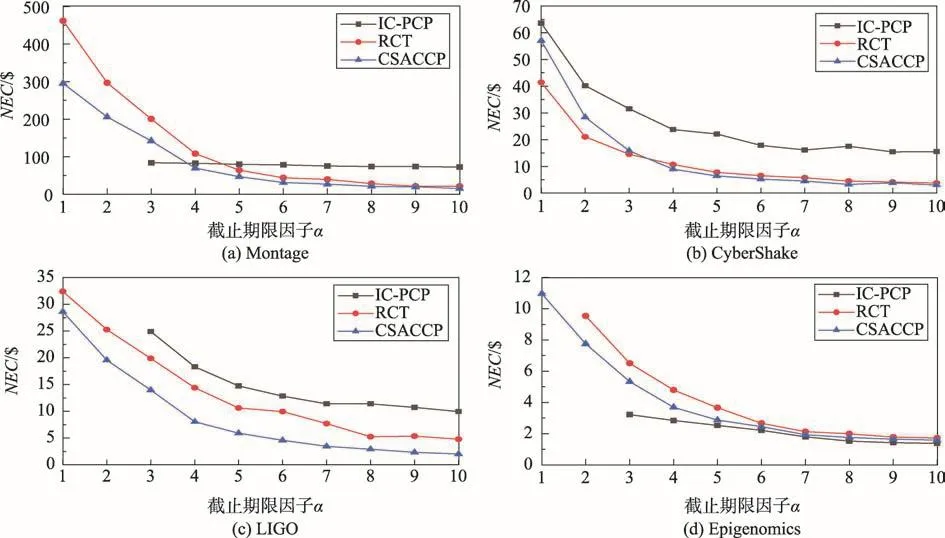
Fig.5 Normalized schedule cost图5 标准化执行成本

在Epigenomics工作流中，IC-PCP虽然在α＞3的阶段内实现了更低的执行成本，但是该算法在大多数的截止期限内，无法满足期限约束完成工作流的调度，尤其是在α足够大的情况下调度成功率也只达到32%，而CSACCP则达到了100%。从图5中可以看出，Montage和CyberShake在严格截止期限内调度产生的执行成本非常高，这是由工作流本身的结构所决定的。在截止期限非常严格时，工作流前两层结构中的任务具有很高的并行度，任务需要并行执行，因此所有算法都需要租用更多的虚拟机实例来完成前期任务，这将导致更高的执行成本。

4.3.5 向上权值对算法性能的影响

CSACCP算法对HEFT中向上权值rank进行了改进，为了分析其对算法性能的影响，设定性能指标执行成本降低率CR（cost reduction rate），计算公式如下：

其中，NECH表示使用HEFT算法中rank的标准化执行成本，NECC表示使用CSACCP算法中ranku的标准化执行成本。

4种不同类型的大型工作流按截止期限因子递增实验结果如表4所示。

Table 4 Average execution cost reduction rate表4 平均执行成本降低率 %

表4中结果表明，对于大型科学工作流，优先调度出度高的任务，在满足截止期限约束的前提下，可以有效降低工作流的执行成本，降低率均在4.6%以上。尤其是对于Epigenomics和LIGO工作流，降低率可达到7.2%以上，这与两种工作流的结构特性有关。两种工作流中都有大量的高出度任务，聚合任务的通信时间，提高任务的优先级，进一步缩短了工作流的执行时间，提高调度成功率。因此，CSACCP算法对向上权值进行改进，并为工作流设定约束关键路径可有效降低执行成本。

总体来看，CSACCP在大多数情况下均可构造更优的调度方案，仅只在LIGO工作流的截止期限中RCT具有略高的调度成功率。在其他场景中，CSACCP均优于IC-PCP和RCT。

5 结束语

为了解决异构云环境下科学工作流截止期限约束的代价优化调度问题，提出一种基于约束关键路径的代价优化算法CSACCP。算法综合考虑云环境下资源异构性、数据通信开销和虚拟机采集延迟等因素。算法对任务设定向上权值，并根据权值将工作流进行分解形成约束关键路径CCP集合，整体分配CCP任务到最便宜实例，并且优先考虑回填策略，进一步提高资源利用率，降低执行代价。实验结果表明，CSACCP算法不仅可以降低执行代价，还可以得到更高的任务调度成功率。在未来工作中，将考虑可靠性、能耗等QoS约束。另外，进一步结合云资源的付费模式，如Amazon的预留模式和Spot模式，提高本文工作流调度模型的适用性。