注重数学整体性 发展学生核心素养的策略方法

摘 要：运用系统、联系的观点对待教学，注重数学整体性，通过对教材重新梳理和编排，整合数学知识内在联系;将学习过程与学生发展终极目标相结合，以知识学习为载体，培养学生数学能力;教学中注重让学生感悟数学思想方法，培养学生数学思维和探究能力，从而发展学生数学核心素养。

关键词：数学整体性;核心素养;策略方法

注重数学整体性是运用系统、联系的观点对待教学，根据数学知识体系、单元主题、数学逻辑关系、数学思想方法与规律、解题思路等内在联系将教学内容加以整合;注重数学整体性是通过抓住知识的内在规律，使学生的学习能力举一反三、触类旁通，达到应有的宽度、广度和深度;将知识盘活，使其可以灵活运用，让学生掌握数学内在规律与方法，培养学生数学思维和探究能力，从而发展学生数学核心素养。

笔者在开展“初中数学单元整体教学研究”和“基于数学核心素养的课堂教学研究与实践”课题研究中，通过对单元教学设计和实施规律的研究与实践，运用系统、联系的观点看待教学，不断总结发展学生核心素养的策略方法。

一、

注重数学整体性，整合数学知识内在联系开展教学，实现高效课堂

加强课标学习，深入研究教材、教法、学法，围绕课程目标用好教材、用活教材、发展教材、整合教材。教师要学会运用系统、联系的观点进行备课和开展教学活动，通过对教材重新梳理和编排，整合数学知识内在联系，有利于激活学生思维，促进学生发展，使教学有的放矢。

案例1 《平行四边形》一章的教学

为了使学生更好地找出和理解知识间的内在联系与变化规律，在教学中进行教材重组。把平行四边形的判定和性质由逐一探究变成整体探究。让学生沿着边、角、对角线三个要素充分认识和理解平行四边形的性质和判定，并能综合利用性质和判定解决具体问题。在此基础上，把矩形、菱形、正方形的性质组合在一起沿着边、角、对角线三个要素探究;把矩形、菱形、正方形的判定组合在一起沿着边、角、对角线三个要素探究。这样整合的目的是让学生找出特殊的平行四边形与平行四边形性质之间、特殊的平行四边形与平行四边形判定之间的关系;明确研究平行四边形的关键要抓住边、角、对角线各元素之间的变化规律，通过类比方法找出知识间的内在联系，提高学习效率;培养学生站在系统的高度理解知识、学习知识，关注数学知识间的联系，从而构建数学知识体系，能够准确地应用知识解决具体问题。

二、

注重数学整体性，将学习过程与学生发展终极目标相结合，培养学生数学能力

数学整体性既体现在数学概念及其蕴含的数学思想方法的一致性上，又体现在各部分内容的有机联系上。从教的角度看，注重数学整体性，才能整体把握教学目标，把数学教得本质而自然，實现“准”“精”“简”的数学课堂，充分发挥数学的育人功能;从学的角度看，注重数学整体性，可以让学生了解知识的源头、发展和去向，掌握数学内容之间的联系，学会用数学思维思考问题、解决问题。在“理解数学，理解学生，理解教学”的基础上开展教学设计和课堂教学，加强数学思考方法的指导，使学生既获得系统性知识，又学会探究的方法，从而提高数学思维能力。

案例2 23.1图形的旋转（1）

“图形的旋转”是人教版九上第二十三章的第1课时，本节课的主要内容是让学生理解旋转的概念及性质。备课时考虑到学生在七下第五章已学过平移，八上第十三章已学过轴对称，而这三部分内容都属于图形的全等变换，从学生的认知水平出发，把这三部分的内容整合在一起，同学们相当于对平移、轴对称知识进行一次充分复习，得到进一步的巩固与提升，是个升华的过程;并且有了平移、轴对称知识作铺垫，对旋转的学习就积累了一定的经验，对顺利完成旋转的学习起到一定的促进作用，学习时就会建立知识间整体的认识，发现联系，关注联系，使学习更系统。另外，由于旋转和平移、轴对称都是全等变换，因此它们不仅在性质的内容上有很多相似之处，而且在性质的探究视角方面也有不少相似之处。因此可以通过类比平移、轴对称的研究内容和研究方法研究旋转，使学生在自主探究中进一步体会类比的研究方法以及图形运动中的变与不变。

三、

注重数学整体性，让学生感悟数学思想方法，培养学生数学思维和探究能力

注重数学整体性，教学中以数学思想为主线，结合数学知识设计问题串，让学生在不断分析问题和解决问题中总结学习方法，培养数学思维和探究能力;让学生通过提炼、总结、理解、应用等循环往复的过程逐步“悟”数学知识、技能中蕴涵的数学思想，提高学生数学素质。

案例3 在“多边形的外角和”探索中设计如下教学活动：

复习提问：

①n边形的内角和是多少？

②什么叫三角形的外角？

③一个三角形有多少个外角？

④什么叫三角形的外角和？

新课导入：

1.

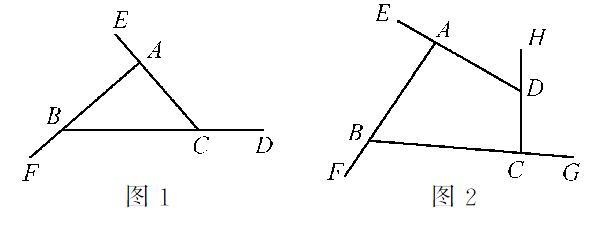
如图1，你能求出三角形的外角和吗？

鼓励学生用不同的方法，及时引导学生归纳结论。

2. 我们已经知道三角形的外角和定义，你能定义四边形的外角和、多边形的外角和吗？

3.

同学们有当数学家的天赋，我们的数学家也是这样定义的。现在我们要探究多边形的外角和，先看简单的，求一个四边形的外角和，如图2所示，应如何进行？

学生会根据刚才求三角形的外角和的思路来求四边形的外角和。及时引导学生归纳结论。

4. 如图3，六边形的外角和等于多少？

追问1：你是怎么计算的？

追问2：猜想n边形的外角和等于多少？你能证明你的猜想吗？

鼓励学生用多种方法证明。

教学反思：

1.

在处理教材时注重数学整体性，关注数学知识联系，引导学生对比“三角形外角和定义”与“三角形内角和定义”，通过“三角形的外角和的定义及推导思路”类比推广到“四边形、六边形、多边形的外角和的定义及推导思路”;联想“三角形内角和定理的证明思路”，用推理的方法证明四边形、多边形的外角和公式;学生经历类比、推广、提炼、总结、猜想、验证、理解、应用的过程，逐步领会学习数学的思想方法，培养学生的推理能力、应用意识和创新意识。

2.

运用类比、推广的方法，设计层层递进的问题串，将复杂问题转化为简单问题、化未知为已知，让学生感悟从特殊到一般、数形结合等思想方法，引导学生从多种角度验证、理解与体会“多边形的外角和恒为360°”的道理，较好地落实“探索并掌握多边形外角和公式”教学要求，培养学生的探索能力。

通过开展“初中数学单元整体教学研究”和“基于数学核心素养的课堂教学研究与实践”的课题研究与教学实践，我们运用系统、联系的观点对待教学，重视认识和解决问题方法的教学：引导学生思考如何获得研究对象;怎样构建研究数学对象的基本线索;逐步学会发现和提出值得研究的具体问题;不断掌握研究问题的基本方法。培养学生学会用数学的眼光观察世界，用数学的思维分析世界，用数学的语言表达世界，不断总结发展学生核心素养的策略方法：注重数学整体性，通过对教材重新梳理和编排，整合数学知识的内在联系，实现高效课堂;将学习过程与学生发展终极目标相结合，培养学生数学能力;让学生感悟数学思想方法，培养学生数学思维和探究能力，从而发展学生数学核心素养。

参考文献：

[1]姜风平，侯丙生.换一种教法：单元整体课程实施与评价（初中数学）[M].济南：山东文艺出版社，2013：241.

[2]章建跃.注重整体性才是好数学教学[J].中小学数学：高中版，2012（4）.

[3]邓秀荫.单元整体教学中渗透数学思想方法的研究[J].中学数学研究，2015（10）：2，14.

作者简介：

邓秀荫，福建省龙岩市，龙岩市第一中学分校。