降雨联合地震下黏土心墙土石坝稳定性分析
米热尼沙·麦麦提
(喀什地区水利水电勘测设计院,新疆 喀什 844000)
1 概 述
中国是世界上地震频发的国家之一,地震灾害给人民的财产安全和生命安全造成巨大的威胁[1]。由地震引发的滑坡灾害就是其中之一,而降雨又加速了这种灾害的发生概率。例如1999年的台湾集集大地震[2]后的强降雨诱发了新的滑坡等地质灾害,降雨诱发的滑坡面积是地震直接诱发的滑坡面积的3倍;汶川大地震也诱发了1.5万处滑坡[3],说明震后的降雨将会诱发更大范围的滑坡。国内外许多专家学者都对地震、降雨或者降雨耦合地震工况下的边坡稳定性进行大量的研究。Premchit[4]在1991年通过研究发现,在香港24 h降雨量超过200 mm时一定会有滑坡发生。Keefer[5]1984年通过对40个历史地震进行研究分析得出, 地震震级不大于4级时不会有滑坡发生;当震级达到9.2级时, 将会在500 000 km2范围内发生滑坡。徐文杰[6]等选用ABAQUS软件, 从三维空间出发对地震诱发肖家桥滑坡的失稳进行了相关的模拟分析, 克服了二维分析方法带来的误差, 且与现实较符。孙军杰[7]认为某种特定条件下 (降雨充沛地区发生特大地震时) , 地震和降雨的持续影响效应可能会对边坡体稳定性产生耦合削弱作用, 由此造成的与滑坡有关的潜在灾害不容忽视。
为了分析研究降雨及地震耦合作用对土石坝边坡稳定性的影响, 本文以某水利枢纽中的黏土心墙坝为工程背景, 采用Geostudio软件模拟分析土石坝坝坡在不同库水位下地震与降雨耦合情况下的稳定性, 为今后类似工程研究提供科学依据。
2 理论背景
2.1 非饱和理论
库水位骤降时,上下游堆石区呈现出典型的饱和-非饱和渗流特性,特别是上游堆石区内的孔压力出现较大的波动,饱和-非饱和渗流[8]的张量形式如下:
(1)
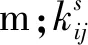
2.2 非线性材料模型
本文进行动力模拟时,采用Geostudio中Quake/w中的非线性材料模型。本文主要研究对象为上下游堆石区,QUAKE/w提供的粗粒土的剪切模量表达式如下:
(2)
(3)
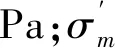
2.3 坝坡永久变形
本文采用1965年Newmark[9]提出的地震下边坡的永久变形分析方法,即同时计算多个潜在滑动面并且计算出最大变形边坡滑动面,在获得最大变形的滑动面后Geoslope计算出安全系数Fs为1时的屈服加速度ay以及该潜在滑动面随时间变化的平均加速度a,对(a-ay)关于时间二次积分即可得到潜在滑动面的Newmark边坡永久位移大小。
3 计算模拟
3.1 工程概况
某水利枢纽工程中的拦河坝为黏土心墙土石坝,从上游到下游依次为上游围堰、上游堆石区、过渡层、黏土心墙、下游堆石区以及下游堆石棱体。坝顶高程为156.20 m,正常蓄水位为152.0 m,死水位为125 m,典型剖面见图1。
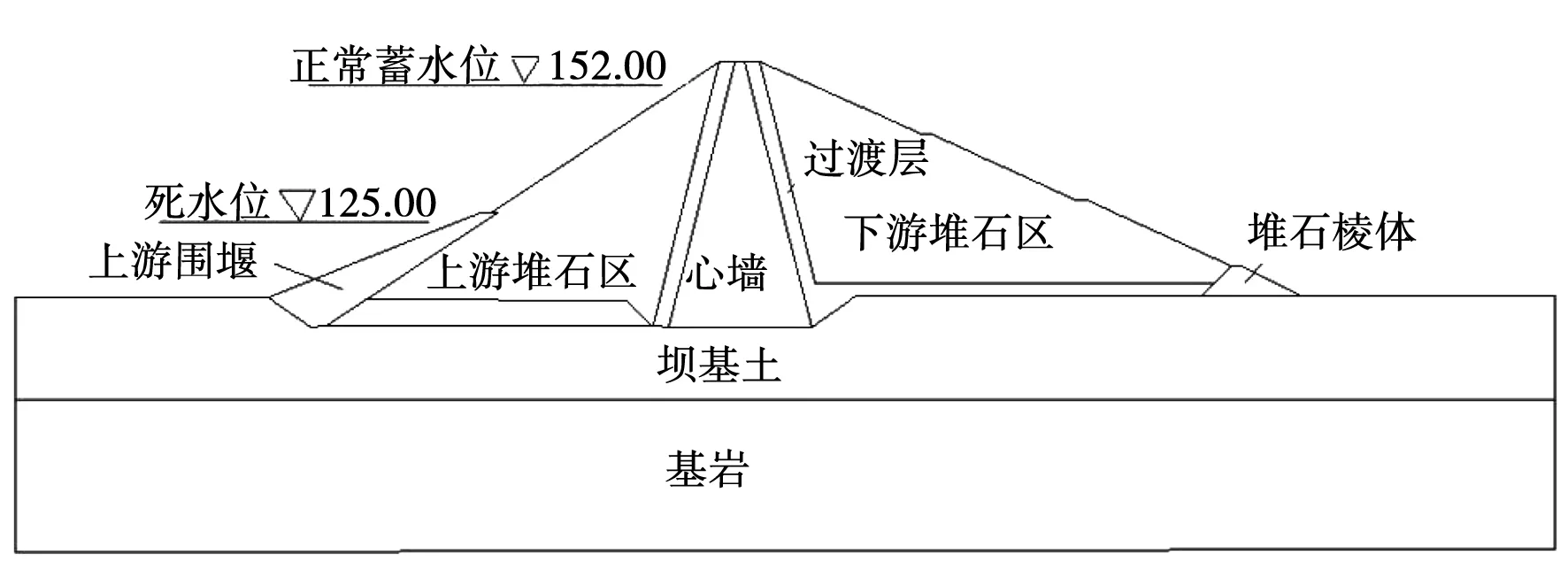
图1 心墙坝典型剖面图
3.2 计算模型
模型网格图见图2。地基厚度为50 m,长305 m,地面高程为0 m,则死水位为15 m,正常蓄水位为42 m。N1、N2、N3上游堆石区内不同位置的监测点。网格单元类型主要为三角形和四边形。为了更准确反映上下游堆石体内不同监测点的孔隙水压力变化,取上下游堆石体和心墙部分的网格尺寸为1.5 m,其余部分取3.5 m,全局共划分3 854个单元,3 896个节点。
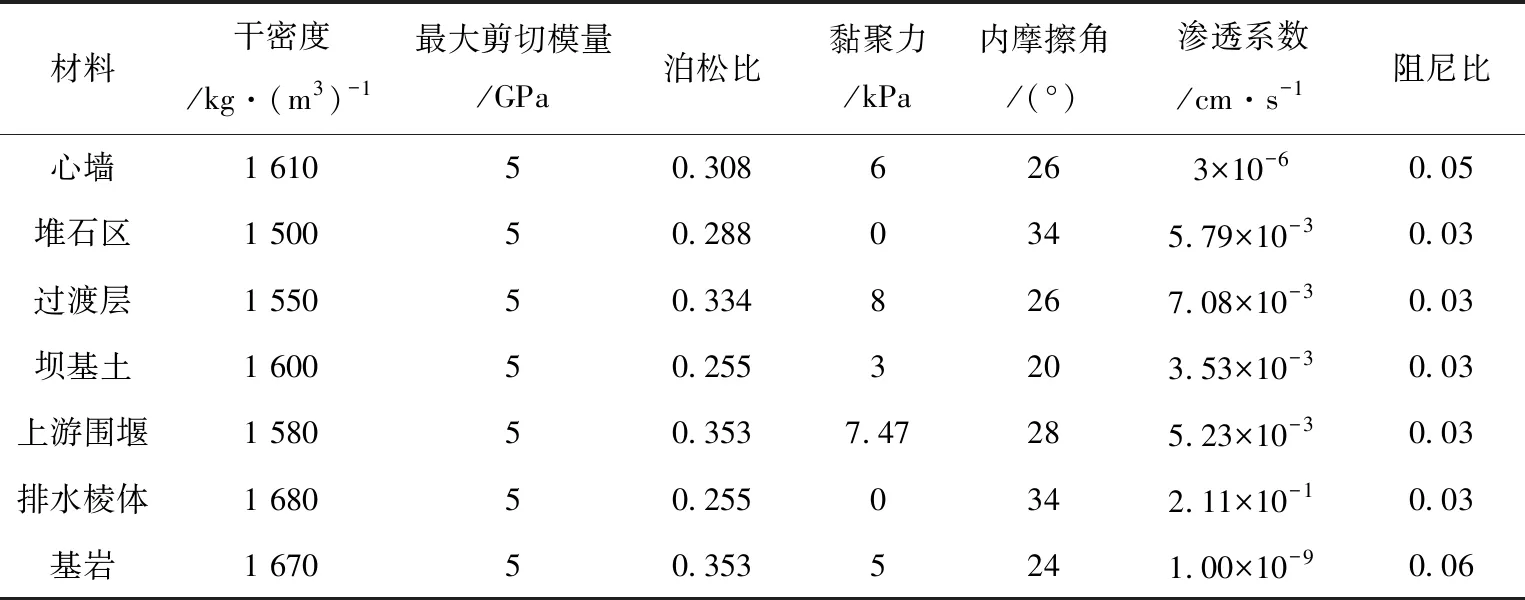
3.3 土体参数
黏土心墙土石坝各区域的物理力学参数见表1。土水特征曲线采用Fredlund&Xing模型, 描述土水特征曲线 (SWCC曲线) 是衡量土体内部渗透系数(体积含水率)与基质吸力之间的关系的重要曲线,见图3。
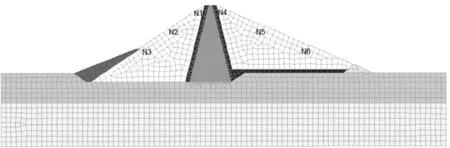
图2 模型网格图
材料干密度/kg·(m3)-1最大剪切模量 /GPa泊松比黏聚力/kPa内摩擦角/(°)渗透系数/cm·s-1阻尼比心墙1 61050.3086263×10-60.05堆石区1 50050.2880345.79×10-30.03过渡层1 55050.3348267.08×10-30.03坝基土1 60050.2553203.53×10-30.03上游围堰1 58050.3537.47285.23×10-30.03排水棱体1 68050.2550342.11×10-10.03基岩1 67050.3535241.00×10-90.06
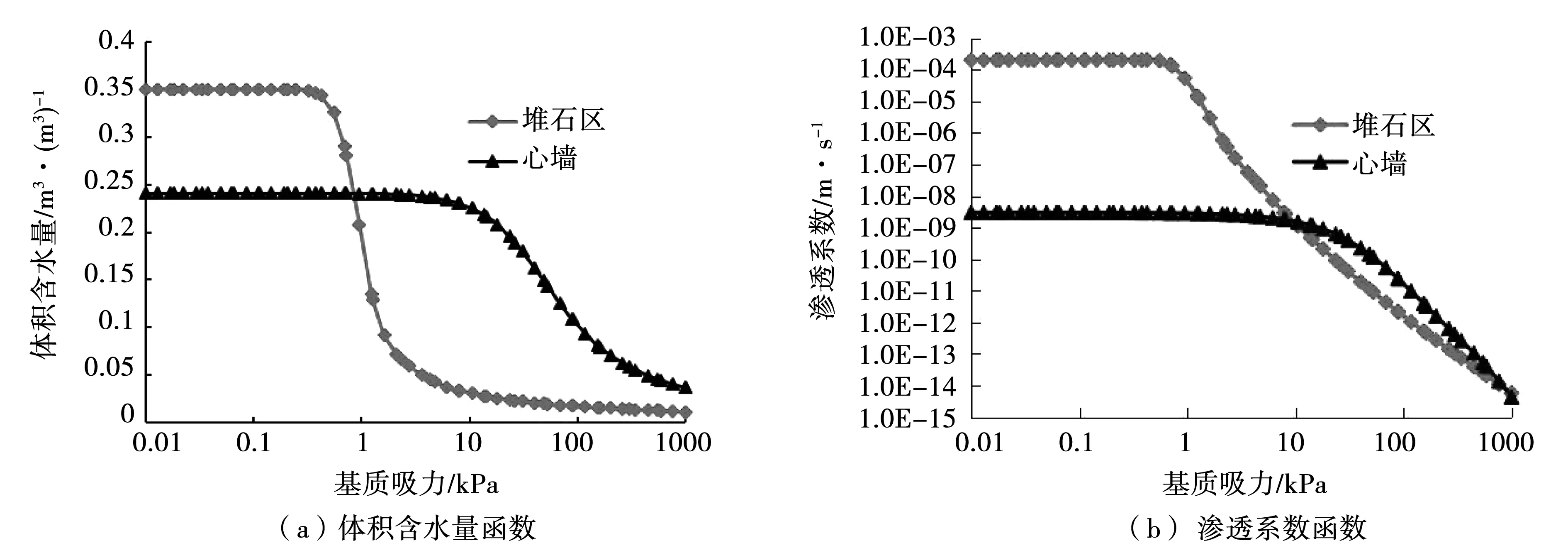
图3 土水特征函数曲线
根据可研性研究报告,库区的地震动峰值加速度为0.10 g,相应的地震烈度为Ⅶ度。本次数值模拟采用国际上常用的EI-Centro水平方向的地震加速度时程曲线,为缩短计算时间截取地震振幅较大的前10 s作为输入波,在对地震波进行滤波以及基线校正处理的基础上,将其峰值调为0.10 g(g=10 m/s2),图4为校正后的加速度时程曲线。
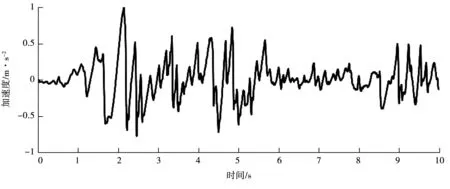
图4 校正后水平向加速度时程曲线
4 计算结果分析
4.1 不同骤降速率上下游堆石区孔隙水压力分析
本文研究的是某黏土心墙土石坝上下游堆石区在不同库水位工况下发生降雨时的渗透特性,以及在降雨过程中遇到地震作用下的上下游坝坡稳定性。降雨强度为0.1m/d,降雨持时为2天,发生在0~2天;地震最大输入加速度为0.1 g,持续时间为10 s,发生时刻为第一天降雨结束时刻;数值模拟时长为10天。N1、N2、N3、N4、N5和N6分别为上下游堆石区内的监测点。从图5可以看出,在死水位工况下,上游堆石区内的监测点孔压总体上呈现先增大后减小的变化规律。由于监测点离上游库水位的距离不同,各个监测点的孔压在降雨过程中的变化也存在差异。监测点离库水位越远,初始孔压力越小,降雨后孔压变化越剧烈。例如,N1、N2和N3的初始孔压力分别为-265.6、-176.7和-18.4 kPa;在降雨发生的一天内,最大孔压力上升到-13.6、-12.2和-9.7 kPa,分别增大95%、93%和34%。这是因为降雨强度比较大,上游堆石区的渗透系数也比较大,大部分降雨入渗到土体内,导致土体的孔压力迅速升高。监测点发生最大孔压力时刻并非停雨时刻,而是在降雨期间。停雨后,各监测点的孔压力缓慢减小,直至计算结束时刻,分别为-41.8、-41.3和-17.1 kPa。对于下游堆石区的监测点来说,监测点离坝体浸润线的距离越远,初始孔压力越小,降雨后孔压力变化越剧烈,达到孔压力最大值的时间越长。例如,N4、N5和N6在降雨期间孔压力达到最大值的时间分别为0.25、1.75和2天。停雨后,监测点的孔压力缓慢减小,计算结束时刻孔压力相差不大。对比上下游同一高度的监测点孔压力可以看出,下游监测点的初始孔压比上游相同高度的监测点小,而且降雨期间孔压力的变化更加剧烈。
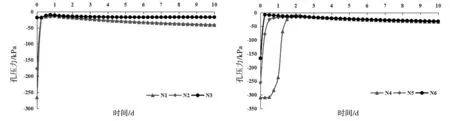
图5 死水位下监测点孔压力图
由图6可以看出,在正常蓄水位工况下,上游堆石区内监测点的孔压总体上保持不变。这是因为当库水位为正常蓄水位时,上游监测点都位于饱和区,降雨对其几乎没有影响。对于下游各监测点来说,其变化规律与死水位工况下的相似。对比不同库水位下下游同一监测点可以看出,死水位下监测点的孔压力小于正常蓄水位,但是到达孔压最大值的时间相对较短,计算结束时刻孔压力更大。
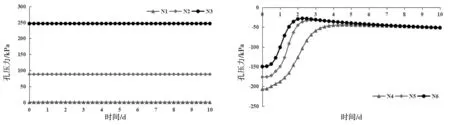
图6 正常蓄水位下监测点孔压力图
4.2 不同库水位工况下降雨偶遇地震上下游堆石区抗震稳定分析
地震可能发生于降雨过程中的任意时刻,所以限于篇幅,本文假定降雨1天结束时刻发生地震。从图7(a)可以看出,总体上正常蓄水位工况下上游坝坡安全系数比死水位工况下大,而且最小安全系数均大于1。由此可见,库水位越高,上游坝坡在地震作用下的稳定性越好。从图7(b)可以看出,正常蓄水位和死水位工况下,上游坝坡的永久变形分别为0和0.025 m。
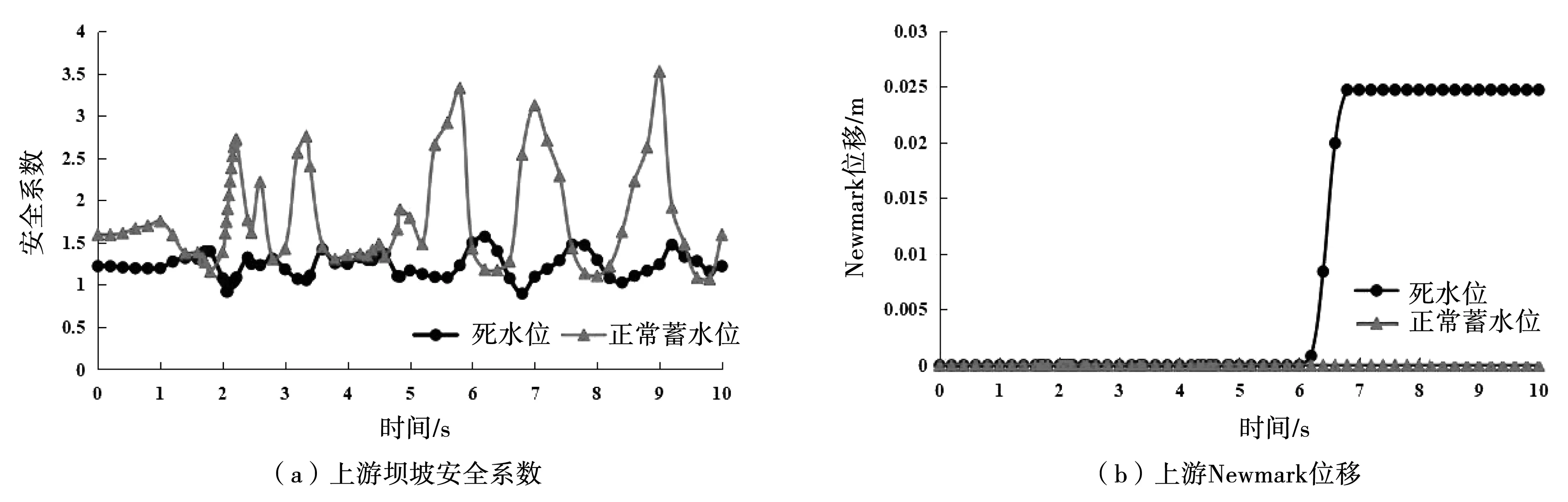
图7 上游动力响应图
从图8(a)可以看出,对于下游坝坡而言,死水位工况下的坝坡安全系数比高水位下大,高水位和低水位下下游坝坡永久变形分别为0.241和0.039 m。由此可见,库水位越高,下游坝坡在地震作用下的稳定性越差。对比上下游坝坡安全稳定系数曲线可得,库水压力可以加强上游坝坡的稳定性,但是水位越高,下游坝坡的稳定性越差。这是由于库水位越高,作用在坡面的水压力越大,增加了上游坝坡的抗滑力。但是库水位越高,下游坝坡的地下水位线越高,下游堆石区的饱和区越大,土体的抗剪强度减小,下游坝坡的抗滑力减小。综上可知,低水位下黏土心墙土石坝的上游边坡为抗震稳定薄弱区,高水位下黏土心墙土石坝的下游边坡为抗震稳定薄弱区。

图8 下游动力响应图
5 结 论
1) 在不同水位工况下发生降雨时,上下游堆石区内的监测点孔压总体上呈现先增大后减小的变化规律,上游堆石区内的监测点离库水位越远,孔压力变化越剧烈;下游堆石区内的监测点离地下水位越远,孔压力变化越剧烈。
2) 在降雨期间遇到地震时,高水位工况下,上游坝坡的安全系数总体上比低水位工况大,而下游坝坡恰恰相反。

