CFD and experimental investigations on the micromixing performance of single countercurrent-flow microchannel reactor☆

Kunpeng Cheng,Chunyu Liu,Tianyu Guo,Lixiong Wen,2,*

1 State Key Laboratory of Organic-Inorganic Composites,Beijing University of Chemical Technology,Beijing 100029,China

2 Research Center of the Ministry of Education for High Gravity Engineering and Technology,Beijing University of Chemical Technology,Beijing 100029,China

Keywords:Single countercurrent-flow microchannel reactor Micromixing performance CFD Villermaux/Dushman reaction

ABSTRACT Microchannel reactors are widely used in different fields due to their intensive micromixing and,thus,high masstransfer efficiency.In this work,a single countercurrent-flow microchannel reactor(S-CFMCR)at the size of～1 mm was developed by steel micro-capillary and laser drilling technology.Utilizing the Villermaux/Dushman parallel competing reaction,numerical and experimental studies were carried out to investigate the micromixing performance(expressed as the segregation index XS)of liquids inside S-CFMCR at the low flow velocity regime.The effects of various operating conditions and design parameters of S-CFMCR,e.g.,inlet Reynolds number(Re),volumetric flow ratio(R),inlet diameter(d)and outlet length(L),on the quality of micromixing were studied qualitatively.It was found that the micromixing efficiency was enhanced with increasing Re,but weakened with the increase of R.Moreover,d and L also have a significant influence on micromixing.CFD results were in good agreement with experimental data.In addition,the visualization of velocity magnitude,turbulent kinetic energy and concentration distributions of various ions inside S-CFMCR was illustrated as well.Based on the incorporation model,the estimated minimum micromixing time tm of S-CFMCR is ～2×10-4 s.

1.Introduction

During the past decade,microchan nel reactors,which can perform chemical reactions in tiny channels with continuous processes [1],have attracted considerable attention.With the channel dimensions in the sub-millimeter level,microchannel reactors achieve process intensification by greatly increasing the specific surface area.It was reported that transport properties in such reactors can be up to two orders of magnitude higher than that in corresponding conventional equipment[2],and the dimensions of microchannels are often an order of magnitude lower than those conventional reactors[3].Microchannels have shown superior heat and mass transfer efficiency.Moreover,the size of the interface between fluids can be precisely and easily controlled[4].These characteristics make microchannels suitable for fast reactions[5],intensive exothermic reactions[6],and even explosive reactions[7,8].A lot of microchannel reactors have been designed elaborately for gas-liquid flow and liquid-liquid folw studies,and attracted increasing attention in both laboratories and commercial areas in recent years[9-13].

Mixing at molecular scale(micromixing)can intensively influence the selectivity, yield and quality of final products in many fields in chemical processes,such as polymerization,crystallization,and organic synthesis[14-16].Micromixing efficiency is a significant performance index for most chemical mixers and acts an extremely crucial role in their design and optimization.To evaluate the micromixing performance, many methods have been proposed [17], among which the chemical reaction methods are the most widely used. By employing mixing sensitive chemical reaction as molecular probes,chemical reaction methods offer distinct advantages over other proposed methods,which can be classified into three schemes:single reaction(A+B →R),consecutive competing reactions(A+B →R;R+B →S),and parallel competing reactions(A+B →R;C+B →S)[18].The iodide-iodate parallel competing reaction[19](known as the Villermaux/Dushman reaction)has been widely utilized for the micromixing characterization of various mixers,working in batch or continuous conditions, with the best sensitivity.Gao et al.presented the application of the Villermaux/Dushman method in characterizing the micromixing efficiency of a T-shaped confined impinging jet reactor(CIJR)at high Reynolds number under different operating conditions[20].They found that the geometric parameters of CIJR play a significant role in its micromixing performance.The investigation of convective micromixing in various mixer structures was carried out with the aim of high mixing intensity and a high throughput mainly based on the Villermaux/Dushman method[21],and a new class of identification number was proposed for characterizing and comparing the effectiveness of different mixing devices.Nevertheless,such an experimental method is not that convenient when it comes to extreme operating conditions or desired tiny size of microchannels.Additionally,detailed local information about fulid folw and concentrations of reaction species as well as the characterizing processes for folw parameters can be hardly obtained via experimental method.

With the spectacular development of computer capacity,numerical simulation based on computational fluid dynamics(CFD)has proven to be a reliable way for both qualitative and quantitative analysis of folw structures,species concentration and mixing performance.CFD approach, although still needing experimental verification, is more economical, efficient and flexible since it can adjust the structure of microchannels and operating conditions accordingly in the simulation process.Therefore,CFD method offers great potentials for the design and optimization of chemical reactors,and has been implemented in investigating the mixing behaviors in microchannels accompanying with experimental method frequently.Soleymani et al.experimentally and numerically studied the flow dynamics and mixing characteristics of liquids in T-type micromixers to optimize the mixing[22].The results indicated that the development of vortices is essential to achieve good mixing performance,which strongly depends on the flow rate and the geometrical parameters of the mixer.The flow and mixing in a zigzag microchannel under rotation were studied by Ren and Leung [23].Their results demonstrated that the overall mixing effciiency of a rotating zigzag channel is considerably better than that of a stationary zigzag channel and a rotating straight channel.In our previous work,a microimpinging stream reactor (MISR) was developed by commercial microcapillary and T-junction and its micromixing performance was investigated experimentally and numerically [24]. The simulation results agreed well with the experimental data and revealed that the two injecting streams impinged intensely at the center of the reactor chamber and could achieve almost perfect micromixing at the inlet Re higher than 3000.Then the application of MISR in the preparation of CuO/ZnO/Al2O3catalysts for methanol synthesis was presented[25]. It was found that both the catalytic activity and selectivity of CuO/ZnO/Al2O3catalysts prepared in MISR were superior to those produced in batch route.However,to achieve the desired micromixing efficiency,MISR requires high liquid flow velocities,which will cause great challenges to the fluid loading capacity and working pressure of the fluid pumps during the number-scaling up of MISR.Therefore,new microchannel reactors with simple structure and excellent micromixing efficiency at low liquid flow velocities are more suitable and needed for commercial-scale production.

In this work,we built a single countercurrent-flow microchannel reactor(S-CFMCR)with steel micro-capillary and laser drilling technology to achieve intensifeid micromixing performance at low liquid folw velocities. The S-CFMCR was constructed with a single steel microcapillary,which was connected with two pumps for the liquid input from both ends and had a laser-drilled outlet at the center position with adjustable size. The two liquid streams flew into each other at the middle of the micro-capillary and got out at the outlet.The mixture was then collected into a container for the subsequent treatments.Such design can also avoid the severe blocking problem of the T-shape or Y-shape microchannel reactors when applied in precipitation reactions,which usually occurs within the tiny outlet channel. Therefore, SCFMCR is a promising and powerful process intensifciation technology with ease of scale-up.It may have great potentials in most applications where microchannel reactors are applicable,including nano/ultrafine particle synthesis, liquid-liquid extraction, precious-metal recovery,organic synthesis and heat transfer processes.

To better understand the flow patterns inside S-CFMCR and the factors affecting the micromixing efficiency,both CFD simulations and experiments were conducted to investigate its micromixing performance by applying the Villermaux/Dushman method.CFD predictions were compared with experimental data in a wide range of operating conditions,including injection Reynolds number(Re),and volumetric flow ratio between the two inlet streams(R).The effects of geometric parameters, e.g., inlet diameter (d) and outlet length (L), on the micromixing efficiency and the pressure drop inside the microchannel were also analyzed. The micromixing time was estimated based on the incorporation model.

2.Experimental

2.1.Materials

The used reactants,their initial concentrations are shown in Table 1,which were prepared according to the previous work[26].All reagents used were obtained from Beijing Tongguang Fine Chemicals Company,and were of analytical grade and used without further purification.The acidic solution was prepared from dilute sulfuric acid.

For preparation of the base solution,sodium hydroxide(NaOH)wasadded into boric acid solution(H3BO3)in deionized water to obtain an equimolar buffer solution of H2BO3-/H3BO3(pH=9.14).Additionally,KI and KIO3were dissolved in deionized water to form a KI/KIO3solution, then added to the buffer solution. This sequence of mixing must be strictly followed so that iodide and iodate ions can coexist in a basic solution,which prevents thermodynamic iodine formation[27,28].

Table 1 Initial concentrations of used reactant

2.2.Micromixing characterization

The micromixing performance of S-CFMCR was characterized using the Villermaux/Dushman method as proposed previously[19],with reported experimental procedure and reaction kinetics[26,29].However,there are still some controversies in the kinetics of the Dushman reaction[30,31].Kölbl and Schmidt-Lehr argued that the choice of the acid or the dissociation constant of sulfuric acid has to be considered for a quantitative analysis of micromixing performance[32].While Commenge and Falk proposed that the use of sulfuric acid would not have much impact even on quantitative investigations [33]. Even so, the iodide-iodate reaction system with the following classic kinetics is still a commonly used reaction scheme to rank different mixer or check effects of varying process conditions on mixing qualitatively.

The reaction formulas are shown as follows:

Eq.(1)is quasi-instantaneous,the kinetics can be expressed as[30]:

For Eq.(2),the kinetics is experimentally determined and can be written as[29]:

Eq.(3)is a reversible reaction whose kinetics can be specified as[29]:

Eq.(1)is quasi-instantaneous while Eq.(2)is very fast but much slower than Eq.(1).The two reactions are competing for H+in the system.In the case of ideal micromixing,H+will be instantaneously distributed homogeneously and completely consumed by borate ions(H2BO3-)to form boric acid(H3BO3)according to Eq.(1),and Eq.(2)will not take place. On the contrary, H+will be involved in both Eq.(1)and(2)and I2will be formed.The formed I2can further react with I-to yield I3-according to Eq.(3).The amount of the produced I3-depends on the micromixing performance,which is expressed in terms of segregation index(XS),and calculated from the following expressions[19]:

where Y is the molar ratio of the acid consumed by Eq.(2)to the total acid injected;YSTis the value of Y in case of total segregation,as follows:

in which,the subscript 0 represents the initial concentration of each component before entering the mixing zone; VAand VBdenote the volumetric flow rates of mixtures A and B,respectively.In this study,mixture A is composed of H2BO3-,I-and IO3-,and mixture B is sulfuric acid solution(H2SO4).

The value of XSis within the range of 0 ＜XS＜1 for partial segregation.The higher XSis,the worse the micromixing status it represents.

2.3.Estimation of micromixing time

The incorporation model was firstly proposed for estimating the micromixing time [34], especially in continuous reactors [35,36].Based on the incorporation model,mixture A is divided into aggregates,which are progressively invaded by fluid of the outside mixture B.The characteristic reaction time of incorporation (tm) is assumed to be equal to the micromixing time.The volume of the aggregate grows according to the law of Q2=Q20g(t),in which g(t)is the incorporation function with the form of a linear relationship of g(t)=1+t/tmor an exponential model of g(t) = exp(t/tm). A simple dilution-reaction scheme was assumed as stated in the following[34]:

where Cjdenotes the concentration of reactant j,Cj10represents the concentration of surrounding liquid,Rjis the reaction term,and g denotes a function controlling the mass exchange rate between the liquid particle and the surrounding liquid.

2.4.Prediction of pressure drop

An empirical formula was employed for predicting the pressure drop within microchannel where the flow is incompressible and laminar,which is expressed as follows[37]:

where Dhis the hydraulic diameter,which is calculated by L;λ is the frictional factor that can be written as:

where f is Fanning frictional factor.

2.5.Experimental apparatus and procedures

As illustrated in Fig.1(a),a single countercurrent-flow microchannel reactor(S-CFMCR)was connected with two high precision constantflux pumps (Beijing Satellite Manufacturer, 2PB00C). The schematic illustration of S-CFMCR is shown in Fig. 1(b), in which a rectangular hole with a depth of half of d and a length of L was drilled in the middle of the steel micro-capillary by laser technology. The diameter d and the outlet length L of S-CFMCR can be adjusted between 0.2-1 mm and 0.2-2 mm, respectively. Streams A (mixture solution) and B (acid solution) were injected at equal volumetric flow rates into S-CFMCR simultaneously by the two high precision constant-flux pumps. Samples were collected at the outlet after the mixing and reaction between streams A and B. The absorbance of I3-was measured using spectrophotometry (Shimadzu UV-2550,Japan) at a wave length of 353 nm with a measurement error less than ±0.3%.

Fig.1.(a)Experimental flowchart for the iodide-iodate tests;(b)Schematic illustration of S-CFMCR.

3.CFD Model

3.1.Mathematical modeling

For simplification,incompressible liquid flow,steady state,negligible gravity,constant viscosity and isothermal conditions of the microchannel flow were applied in the simulation processes.The governing equations for continuity,momentum,and species in the computational domain were expressed as follows:

Continuity equation:

x-momentum equation:

y-momentum equation:

z-momentum equation:

Species transport equation:

In the above equations,ρ is the fluid density, v→is the velocity vector,υ is the kinematic viscosity with the unit of m2·s-1,p is pressure,T is temperature,k is the effective thermal conductivity;u,v and w denote the velocity component in the x,y and z directions,respectively;Fx,Fyand Fzare the corresponding body force in each direction; ciand Distand for the volume concentration and the diffusion coefficient of species i,respectively.Siis the amount of species i produced by reactions in unit time and physical volume,namely production rate.

The flow field in the reactor was calculated by solving the renormalization group(RNG)k-ε model which accounts for the turbulent effect in the present work.The RNG k-ε model is a modification of the standard k-ε model which gives improved description for viscous flow at low Reynolds numbers.Turbulent kinetic energy,k,and turbulence dissipation rate,ε,can be expressed according to Eqs.(15)and(16),respectively[38-40]:

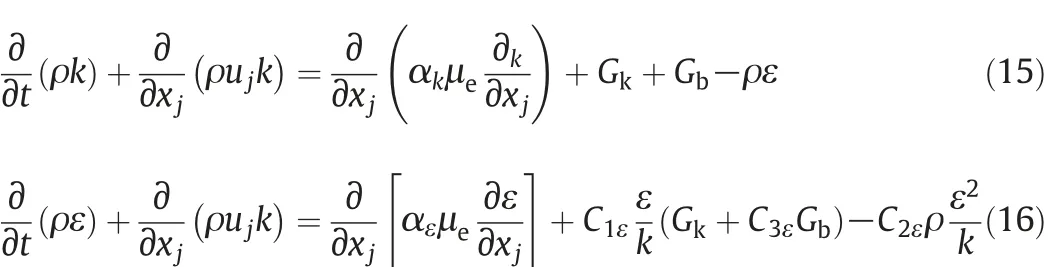
In these equations,Gkand Gbare the generation of turbulence kinetic energy due to the mean velocity gradients and buoyancy,respectively.The RNG theory gives the values of constants as C1e= 1.42, C2e=1.68. The quantities of αkand αεare the inverse effective Prandtl numbers for k and ε,respectively.

3.2.Physical model and boundary conditions

Fig.2.Physical model of S-CFMCR displayed in Fluent.

The 3D geometry of S-CFMCR used in our CFD simulations is shown in Fig.2.For the visualization of flow field and the molar concentration distributions of various species at the outlet of S-CFMCR,a virtual and sufficient cuboid space for the fluid flow was added at the outlet.The wall shear stress of the added block was 0 and the liquid would not be limited when flowing down.The components of streams A and B were defined as the same as those of experiments. It was specified that stream A entered the reactor from the left inlet while mixture B from the right one.Due to the low Reynolds number at low velocities,the flow in S-CFMCR is within the laminar flow regime.In the simulation process,most species defined exist in the aqueous solutions as ions,and liquid water in both mixtures A and B accounts for more than 99%of the volume in the solutions.Consequently,in order to simplify the calculation,both liquids were assumed to have identical physical properties(ρ=998.2 kg·m-3,and μ=1.0 mPa·s).

The microchannel structure was created in Gambit 2.4.6,which is a pre-processor and an integrated package for CFD analysis in Fluent.The computational domain was meshed by Gambit,which consisted of two inlets and one outlet.To make certain that the simulation results were independent of mesh size,various mesh schemes with different grid sizes were tested by both macroscopic (the “cold-flow”, or unreactive flow)and microscopic(Villermaux/Dushman scheme was employed based on“cold-flow”simulation)methods,to calculate the final values of different variables at the outlet of S-CFMCR.As illustrated in Fig. 3, it was found that there were no significant changes in the values of the investigated variables when the average size of cell reached 0.03 mm, corresponding to a total mesh number of about 2.7 million.A uniform velocity profile was assumed at the two inlets and the pressure outlet boundary condition was applied at the exit.In addition,no-slip boundary conditions were assigned for the solid walls.

3.3.Calculation procedure

The commercial solver ANSYS Fluent 14.0 was used for the CFD investigation,which solves Navier-Stokes equations with finite volume method.The flow was assumed to be steady and Newtonian.Diffusion coefficients (Di) for each of the species were in the order of 1 ×10-9m2·s-1with a viscosity at 1.0 mPa·s. The computations were conducted in two steps: 1) the continuity, momentum, energy and species equations were solved numerically with reactions disabled to obtain a stable flow field;2)the reactions were implemented and the calculation was continued based on the first step.In the second step,the Villermaux/Dushman reaction kinetics scheme was implemented by utilizing the species transport equation.Considering I3-could only be formed by the consumption of I2(Eq. (3)) and Y is expressed by the total concentration of I3-and I2,only Eqs.(1)and(2)were involved into the simulation process for the estimation of Y. Thus, the total concentration of I3-and I2in Eq.(5)was replaced by the concentration of I2in the simulations.

In the present work,simulations were performed in ANSYS-Fluent framework.PRESTO!scheme was implemented for pressure discretization and for the other dependent variables.Second-order upwind schemes were applied to calculate the velocity and pressure fields by the SIMPLE(Semi Implicit Pressure Linked Equation)algorithm.The solution was considered to have achieved convergence when the residuals of all equations were less than 10-6.

Fig.3.Independence check of mesh size:macroscopic test(left)and microscopic test(right).

4.Results and Discussion

4.1.Flow patterns and concentration distribution inside the S-CFMCR

Figs.4 and 5 represent the contours of liquid velocity profile and turbulent kinetic energy, respectively, at four different VA(volume flow rate of mixture A)from 10 to 70 ml·min-1,which correspond to Reynolds numbers(Re)ranged from 202 to 1414 when the inner inlet diameter(d)is 1.0 mm.Here,Re is expressed with the average liquid velocity in the inlet:

As shown in Fig.4,the flow was strictly laminar(stratified flow)at very low Reynolds numbers in the inlet zone with distinct turbulent vortexes appeared in the convection zone away from the exit. The velocity profile was nearly parabolic with a maximum velocity at the center of the inlet channels due to Newton's law of viscosity. With increasing inlet volumetric flow rate in S-CFMCR, convective mixing was much easier to be achieved while stronger sputtering of fluid was also observed at the exit.Within the computational zone of the model,the flow field was symmetrical on the convection surface.According to the state of the fluid movement at the mixing region,the fluid field can be divided into three regions: convection zone,vortex zone and exit zone.In the convection zone,the two fluid streams collided into each other and their velocities decreased continuously to the minimum value; in the vortex zone, due to the effect of inertia, vortexes were formed above the exit and other flow units were involved after convective colliding,causing part of the fluid flowing backward to the inlets in the near wall area and then being merged into the incoming streams repeatedly; in the exit zone, the fluid flowed down out of the outlet after mixing.

Fig.4.Contours of velocity magnitude(m·s-1)in midplane(z=0):(a)Re=202;(b)Re=606;(c)Re=1010;(d)Re=1414.

Fig.5.Contours of turbulent kinetic energy(m2·s-2)in midplane(z=0):(a)Re=202;(b)Re=606;(c)Re=1010;(d)Re=1414.

Fig.6.Contours of molar concentration(mol·m-3)of various species at Re=1010 in midplane(z=0):(a)H+;(b)H2BO3-;(c)H3BO3;(d)I2.

The distributions of turbulent kinetic energy are illustrated in Fig.5.They demonstrated that the two injected mixtures encountered in the center of the microchannel,forming a convection zone where turbulent kinetic energy was promptly generated and dissipated.The turbulent kinetic energy had a peak value at the interface of mixtures(0.11 m2·s-2at Re=202,0.99 m2·s-2at Re=606,2.32 m2·s-2at Re=1010,and 4.01 m2·s-2at Re=1414,respectively).In addition,the turbulent kinetic energy in the mixing region increased and got more concentrated with the increase of Re,indicating a better mixing performance.

Fig.6 displays the molar concentration contours of various species at Re=1010.Since reaction(1)is quasi-instantaneous and reaction(2)is fast but much slower than reaction(1),H+(Fig.6a)ions will be consumed by H2BO3-(Fig. 6b) instantly to form H3BO3(Fig. 6c). For a reacting system with perfect micromixing,H+ions fed at stoichiometric amount will be completely consumed by borate ions(H2BO3-)according to reaction(1),and no iodine(I2)will be formed(Fig.6d).In other cases,local excess of H+ions will be achieved after complete consumption of the local H2BO3-,and subsequently I2species will be formed by reaction(2).Thus,the concentration contours of various species of the competing chemical reaction system can reflect the mixing behaviors within S-CFMCR.As illustrated in Fig.6,H+was consumed completely and instantaneously.Meanwhile,the formation of I2could be hardly observed at the outlet and the concentration magnitude of I2was extraordinarily low, indicating a superior micromixing performance under such condition.

4.2.Effects of operating conditions on XS

4.2.1.Effect of inlet Reynolds number on XS

Fig.7 shows the effect of inlet Reynolds number on the micromixing of S-CFMCR.The small values of Xs within the whole Re range indicated that quick micromixing was achieved for all the investigated liquid velocities.Overall,the micromixing was intensified with rising Re,due to the increasing dissipation of turbulent kinetic energy when the two liquid streams collided into each other.However,no further intensification of micromixing could be observed after the increasing Re reached 1200. The simulations agreed well with the experimental results but with noticeable divergence at the low Re regime,probably due to finding that the turbulence was weakened significantly at low Re while the CFD simulations were still proceeded with turbulent models. In addition, compared with the previous micromixing results of MISR,which can only achieve quick liquid micromixing at high liquid velocities,same value of XSwould be obtained at much lower liquid velocities for S-CFMCR when the other conditions were the same.For example,XSreached 0.01(meaning a very quick micromixing performance)when the inlet liquid velocity was increased to 1.05 m·s-1and 2.46 m·s-1for S-CFMCR and MISR[24],respectively,indicating quicker micromixing in S-CFMCR than in MISR at low liquid velocities.

Fig.7.Effect of Re on XS.

4.2.2.Effect of volumetric folw ratio on XS

To investigate the effect of the volumetric flow ratio between the two injected fluid streams(R,defined as VA/VB)on XS,the volumetric flow rate of the acid solution(VB)was adjusted with a fixed flow rate of the base solution(VA).When R was increasing(meaning decrease in VB), the concentration of acid CBshould be increased to maintain the fixed stoichiometric mole ratio of borate ions in mixture A to acid ions in mixture B,i.e.,nA/nB=VACA0/VBCB0.Accordingly,R=1,2 and 3 corresponds to [H+]0in stream B as 0.05, 0.10 and 0.15 mol·L-1,respectively. Fig. 8 illustrates the relationship between XSand Re at the three different volumetric flow ratios obtained from both experiments and simulations.It revealed that XSincreased substantially with increasing R.This phenomenon may be ascribed to the bigger volume difference between the two mixtures at higher R, which results in a heterogeneous mixing between them.Moreover,a larger R corresponds to higher initial H+concentration in mixture B,which will easily cause local excess of acid to borate ions and the excessive acid will be consumed by reaction(2)to form more iodine,leading to the increase of XS.

Fig.8.Effect of volumetric flow ratio R on XS.

4.3.Effects of geometry parameters of S-CFMCR on XS

4.3.1.Effect of inlet diameter on XS

The inlet diameter d of S-CFMCR was chan ged to investigate its effect on the micromixing performance as shown in Fig.8,where the segregation index XSwas plotted against d at a fixed liquid velocity of 0.4 m·s-1.CFD simulations were carried out at six different d ranging from 0.5 to 2.0 mm and experiments were performed at four different d of 0.5,0.8, 1.0 and 1.3 mm, respectively. Other operating conditions were maintained the same. Fig. 9 demonstrates that XSdecreased greatly with increasing d,which is because that a larger d corresponds to larger Re at a constant liquid velocity,and thus,a quicker micromixing performance was achieved as described earlier. As a result, increasing d at microscale led to superior micromixing effciiency of S-CFMCR.

4.3.2.Effect of outlet length L on XSand pressure drop

Fig.9.Effect of inlet diameter on XS at constant liquid flow velocity(u=0.4 m·s-1).

In order to evaluate the effect of the outlet length L on the micromixing performance, the values of XSobtained from CFD and experiments, respectively, were compared at six different L varying from 0.5 to 2.0 mm.When all experimental and simulated conditions but L were the same, as shown in Fig. 10, XSincreased significantly with increasing L at a fixed liquid velocity,indicating that expanding the length of outlet would weaken the micromixing performance dramatically.The mixing within S-CFMCR occurred mainly in the converging region of the two liquid streams. When L was increasing, bigger parts of the two liquid streams would flow out of the tube from the big outlet before they collided into each other,resulting in larger XSand more segregation between the two liquid streams.Overall,the experimental and simulating results of XSagreed well with each other,and the slight difference between them might be attributed to the deviation introduced to both experimental and CFD processes.

Fig.10.Effect of outlet length L on XS at constant liquid flow velocity(u=0.4 m·s-1).

Although the micromixing performance of S-CFMCR can be enhanced by decreasing L,the pressure drop(meaning energy consumption)may rise dramatically as well and needs quantitative analyses. Therefore,the pressure drops in four microchannels at various L were studied by utilizing an empirical formula as demonstrated in Section 2.4.

As a comparison,CFD simulations were also conducted to calculate the pressure drop at different liquid velocities in the range of 0.2-1.0 m·s-1.Fig.11 shows that the predicted pressure drop against velocity in four different microchannels agreed very well with the simulated results,indicating the reliability of the simulations.Both simulation and prediction illustrated that the pressure drop increased with increasing liquid velocity at the inlet.Meanwhile,the pressure drop increased substantially with decreasing L at the same liquid velocity. Therefore,a balance between the micromixing efficiency and pressure drop within S-CFMCR should be taken into account when designing such microchannel reactors,which can be achieved by adjusting the reactor configurations according to various operating conditions.

Fig.11.Comparison between pressure drops predicted by formula and by CFD at different liquid flow velocities.

4.4.Micromixing time

The mass conservation and the reaction kinetics of the Villermaux-Dushman method were adapted into the incorporation model, as shown in Section 2.3,to obtain the relationship between micromixing time tmand segregation index XSat specified experimental conditions,as demonstrated in Fig.12.It can be seen that XSin S-CFMCR ranges from 0.0053 to 0.0007,corresponding to tmof 0.0018-0.0002 s,which suggests that S-CFMCR possesses much superior micromixing efficiency than conventional stirred tank (0.02-0.002 s) [34]. The exponent correlation of them was plotted by linear regression with the result as follows:

where the correlation coefficient is 0.99996 and the standard deviation is 0.01.

Fig.12.Relationship between XS and tm.

Therefore, the relationship between the micromixing time (estimated from the experimental XSas in Fig.7)and Re could be obtained as represented in Fig.13.It shows that tmdecreases with increasing Re,and tmis lower than 0.0006 s at a Reynolds number Re of about 800,demonstrating a very high micromixing efficiency.

Fig.13.Relationship between tm and Re.

5.Conclusions

In this work, a single countercurrent-flow microchannel reactor(S-CFMCR)with the diameter of ～1 mm was developed for achieving quick micromixing at low liquid flow velocities.Its micromixing performance with various operating conditions and structure parameters was evaluated by both experiments and CFD simulations based on the iodide-iodate test reaction. The contours of velocity magnitude,turbulent kinetic energy and molar concentrations of various species were obtained to demonstrate the micromixing efficiency.CFD results were in good agreement with experimental data and indicated that the micromixing efficiency could be intensified by increasing liquid flow velocity and/or decreasing outlet length. In addition, the best micromixing performance was achieved when the volumetric flow rates of the two liquid streams were identical.Although the micromixing efficiency can be enhanced by decreasing the outlet length,the pressure drop within the microchannel would be increased dramatically at the same time. Therefore, optimal outlet length should be applied at various operating conditions to achieve a balance between micromixing efficiency and energy saving. Based on the incorporation model, the micromixing time tmof S-CFMCR was estimated as 0.0002-0.0018 s within the Re range of 200-1400, which is much quicker than most conventional mixing devices.

Nomenclature

Didiffusion coefficient of species i

d inner inlet diameter of S-CFMCR,mm

Fxbody force in x direction

Fybody force in y direction

Fzbody force in z direction

k turbulent kinetic energy,m2·s-2

kjkinetic constant of reaction j

Δp pressure drop,Pa

R volumetric flow ratio

Re Reynolds number of inlet jet

Siamount of species i consumed or produced by reactions

T temperature,K

u fluid velocity,m·s-1

VAvolume flow rate of mixture A,ml·min-1

VBvolume flow rate of mixture B,ml·min-1

XSsegregation index

Y selectivity of iodide

YSTselectivity of iodide for total segregation

μ viscosity,mPa·s

μteddy viscosity,mPa·s

ρ fluid density,kg·m-3

υ kinematic viscosity,m2·s-1