Assessment of the TFM in predicting the onset of turbulent fluidization☆

Musango Lungu,Haotong Wang,Jingdai Wang,*,Ronald Ngulube,Yongrong Yang,Fengqiu Chen,John Siame

1 State Key Laboratory of Chemical Engineering,College of Chemical and Biological Engineering,Zhejiang University,Hangzhou 310027,China

2 Chemical Engineering Department,School of Mines and Mineral Sciences,Copperbelt University,10101 Kitwe,Zambia

Keywords:CFD Fluidization Regime identification Slugging Turbulent Wavelet analysis

ABSTRACT Accurate prediction of the onset of turbulent fluidization still remains elusive owing to the dependence of the transition velocity on several factors including measurement methods and interpretation of results. In this work,numerical simulations using the two fluid model(TFM)are performed in an attempt to predict the regime change reported by Gopalan et al.(2016)in a small scale pseudo-2D gas-solid fluidized bed containing Geldart D particles.Various time and frequency domain analyses were applied on predicted absolute and differential pressure time series data to reveal the bed dynamics.Numerical predictions of the transition velocity,Uc are in reasonably good agreement with experimental results from the small scale challenge problem. The literature correlations completely fail to predict the transition velocity for the system considered in this work.This work thus provides a different approach for validating the CFD model against experimental measurements.

1.Introduction

The onset of fluidization occurs when the weight of the particle bed is balanced by the drag force of the upward moving gas[1].The superficial gas velocity at which fluidization is first observed is known as the minimum fluidization velocity,Umf.Different flow regimes can be observed with increasing superficial gas velocity i.e.fixed bed(delayed bubbling),bubbling,slugging,turbulent,fast fluidization and pneumatic conveying[2,3].Slugging flow is normally encountered in columns with H/D ＞2 which is typical for Geldart D particles.

From the stand point of reactor design it is imperative to demarcate the boundaries for the different flow regimes because parameters like pressure drop,solid hold-up,interfacial area and transport coefficients to a larger extent depend on the flow regime[4].Of the different flow regimes,the turbulent regime is the choice of operation for most key commercial catalytic processes,non-catalytic reactions such as roasting of ores in the metallurgical industry and physical operations such as drying[5].According to Nedeltchev[6]there is currently no reliable method for identification of the boundaries of the main flow regimes in industrial multiphase reactors and therefore more research is warranted.Regime transition identification remains a topic of great interest in the fluidization community.For given physical and operating conditions,flow regime maps have been proposed throughout open literature [2,7,8] to demarcate the boundaries between the different flow regimes,however their usefulness is limited due to several reasons such as poorly demarcated boundaries and limited experimental data.

Other tools available for characterization and demarcation of fluidization regimes are based on the analysis of time series signals grouped into three categories i.e. time domain methods, frequency domain methods and state space methods.Excellent reviews by Johnsson et al.[9], van Ommen et al. [10] and Sasic et al. [11] provide a treatise on these methods as applied to gas-solid fluidization. Time domain methods includes statistical moments,probability distributions,cycle time, rescaled range analysis and the associated V-statistic and autoregressive models.Frequency domain methods involves the analysis of frequency distribution using the Fast Fourier Transform,FFT and identifying the so-called dominant or fundamental frequency which represents the gas voids or slug passage through the bed.Regime transition is identified by a change in the frequency distribution of the power spectra.Wavelet transform similar to short time or windowed Fourier transform is finding increased usage.State space analysis is concerned with the non-linear behavior of multiphase reactors.The gassolid flow in fluidized beds is typically chaotic and exhibits non-linear dynamics and therefore state space methods including attractor reconstruction,entropy,correlation dimension,Lyapunov exponents and attractor comparison are applied to obtain information such as the complexity of the signal,predictability,sensitivity to initial conditions and infinitesimal changes in the signals over time[10].

Pressure fluctuations are almost exclusively used for characterizing dynamics of multiphase reactors due to the ease of measurement even in the hostile industrial environment moreover measurements from pressure drop fluctuations are non-intrusive and reliable in comparison to measurements from intrusive probes such as fiber optic particularly outside the fully developed flow region as recently demonstrated by Cocco et al.[12].Fan et al.[13]were one of the earliest researchers to use pressure fluctuations to characterize fluidized bed dynamics.They applied statistical moments,correlation analyses,probability distributions and FFT to pressure fluctuations.The causes of the fluctuations were explored and so were the influences of gas velocity,bed height,particle size and distributor design on the major frequency and amplitude of fluctuation. Numerous other studies [14-19] have been conducted to identify and characterize fluidization regimes using analyses of pressure fluctuations,the references cited herein are just a handful of those reported in the open literature.

Other researchers have used alternative signals to pressure fluctuations;Zhu et al.[20]utilized solid holdup signals from fiber optical reflective probes to identify flow structures and regime transitions.Makkawi and Wright[21]classified fluidization regimes in a conventional fluidized bed using solid fraction fluctuation measured using electrical capacitance tomography(ECT).de Martin and co-workers[22]detected regime transition in a gas-solid fluidized bed using low frequency accelerometry signals and proposed this as an alternative to conventional pressure signals.Azizpour et al.[23]used vibration signature analysis for characterization of fluid bed dynamics.Wang et al.[24]and more recently Zhou et al.[25]have made use of acoustic emission signals for characterization of flow patterns in gas-solid fluidized beds.Nedeltchev[6]identified the boundaries between the main hydrodynamic boundaries in bubble columns and fluidized beds using photon count time series generated from radioactive technique.

From the foregoing,it is quite evident that identification and detection of flow regimes have been mostly studied using experimental setups.However some of these experimental procedures are quite expensive to set up and not all are suitable and reliable for practical industrial usage.The computational fluid dynamics(CFD)approach can be exploited as a complementary tool to experimentation[26]for the characterization and identification of flow regimes.This is due to the decreasing cost of computational hardware and improved models and computational algorithms.There are several advantages of using CFD including lower costs and the ability to extract a wealth of information from a single simulation.Moreover regime transitions are associated with flow instabilities[6]and CFD being a fundamental based approach can greatly help in understanding the mechanisms responsible for the instabilities that lead to the formation of different flow regimes.

Different CFD models are available for simulating gas-solid flow in fluid beds but the most widely used are the two-fluid Eulerian-Eulerian model(TFM)and the discrete particle model(DPM).The TFM is an extension of single flow models and it assumes both the dispersed and continuous phases as fluids which are fully continuous and interpenetrating.Kinetic theory of granular flow(KTGF)models are used to describe the dispersed phase rheology.The DPM on the other hand offers a higher resolution in comparison to the TFM since it requires fewer closure models but penalizing on computational demand.Instead fluidparticle and particle-particle interactions are tracked thus capturing details of the flow field more accurately.In recent times there has been a research drive in developing so-called coarse grained DPM models with the goal of cutting down the computational demand but in the foreseeable future TFM will most likely continue to be widely used.

Chalermsinsuwan et al.[27]observed both conventional and unconventional fluidization regimes in a high solid CFB(circulating fluidized bed)riser by the use of TFM simulations.They went on further to characterize and map the regimes using normal Reynolds stresses,granular temperatures and other system parameters.Qiu et al.[28]studied different flow regime characteristics in an annular combustion chamber using pressure fluctuations from experimental measurements and computational particle fluid dynamics (CPFD) models. The results from the measurements and simulations were in good agreement.Salikov et al.[29]combined experimental studies and CFD-DEM simulations in the study of a prismatic spouted bed.Different dense operational regimes were identified using frequency domain and state space analysis of pressure fluctuations. Ramirez et al. [30] used the MFIX code to study the transition from bubbling to slugging fluidization in a laboratory scale fluidized bed with Geldart B particles.

The present work is based on the fourth installment of a series of socalled challenge problems.These problems are designed with the view of assessing the predictive capabilities of CFD models by providing experimental test cases for different scenarios that best encompass the challenges in granular-fluid flows[31].Particulate Solids Research Inc.(PSRI)and the National Energy Technology Laboratory(NETL)have collaborated over the years to provide such cases to the modeling community.For the first challenge problem posed in 1995 at the Fluidization VIII conference, the TFM simulations of Sun and Gidaspow [32] predicted a maximum in the solids flux that occurred between a riser wall and its center which was unknown to the modelers at the time but at the same time many models failed to capture the axial pressure profile.Therefore the challenge problem highlighted the strengths and weaknesses of the CFD codes which is also true for the challenge problems that followed[33,34].This exercise is extremely useful for the development and fine tuning of CFD models in order to increase their reliability and usefulness for practical reactor design.For the current challenge problem, we have focused on assessing the ability of the TFM simulations in predicting regime change from slugging to turbulent fluidization observed in the small scale rectangular fluidized bed[35]using time series analysis unlike previous works that have mostly used mean axial and radial profiles of flow field quantities such as solids flux,particle velocity and pressure.Moreover gas-solid flows are highly non-linear and chaotic exhibiting flow structures of different length and time scales and thus we have included a multiscale approach in the detection of the regime change.The numerical predictions for different operating conditions are compared with those from experimental measurements thus providing a different approach for validating CFD codes.

2.Experimental

The experiments were carried out in a rectangular fluidized bed column made of acrylic with dimensions of 0.075 m depth,0.23 m width and 1.22 m length and is shown in Fig.1. These dimensions create a 2D flow because the thickness is much smaller than the height and width.

The bed material consisted of nylon beads with a minimum fluidization velocity,Umfof 1.05 m·s-1determined from the standard pressure drop versus flowrate method [1], Sauter mean diameter of 3256 μm(Geldart D particle type)and a size distribution shown in Fig.2.The remainder of the physical properties are presented in Table 1 and it is worth noting that these properties were calculated by the challenge problem investigators and provided to modelers.The bed was fluidized with air at a pressure of 101.325 kPa and temperature of 20°C at superficial gas velocities of 2.19 m·s-1,3.28 m·s-1and 4.38 m·s-1corresponding to approximately 2Umf, 3Umfand 4Umfrespectively. The terminal velocity of the beads is approximately 9.5Umf[36,37] and therefore elutriation of particles from the bed at the given operating conditions is nonexistent.Therefore no equipment for capturing elutriated particles was installed leaving the top of the column open to the atmosphere.Eulerian particle velocity measurements were taken at five lateral positions of 0.02356 m, 0.06928 m, 0.115 m, 0.16072 m and 0.20644 m at a height of 0.0762 m above the gas distributor using HsPIV [38] at sampling rates of 1,1.2 and 1.5 kHz for total sampling times of 21.096 s,17.88 s and 14.665 s respectively for the three cases.The granular temperature due to particle fluctuations was calculated from the Eulerian particle velocity measurements.

Fig.1.2D schematic of the rectangular bubbling fluidized bed.

Fig.2.Nylon beads cumulative particle size distribution.

Table 1 Particle properties

The low frequency differential measurements were done using a low pressure transducer(Rosemount 1151DP smart transmitter)and the signal was acquired at a frequency of 1 Hz.Meanwhile the high frequency fluctuations were measured with a Setra differential pressure transducer between the taps at heights of 0.0413 m and 0.3461 m above the distributor at a frequency of 1000 Hz and total sampling time of 300 s giving 300000 samples for each operating condition.Detailed description of the small scale challenge problem is available at https://mfix.netl.doe.gov/experimentation/.

3.Model Description and Simulation Set-up

The Euler-granular model available in the commercial code ANSYS Fluent 15 was used for the numerical simulations.The model equations are presented in Table 2.This model treats the continuous fluid and dispersed solids as continuous and fully interacting.The particle-particle interactions are accounted for using the kinetic theory of granular flow(KTGF)which is analogous to the kinetic theory of gases.This theory incorporates the concept of granular temperature which is a measure of the kinetic energy contained by the fluctuating solid particles.Applying appropriate initial and boundary conditions,the mass and momentum conservation equations were solved on a 2D computational mesh together with the partial differential equation(PDF)for granular temperature in the finite volume framework.

The 2nd order upwind scheme was used to discretize momentum and granular temperature equations and QUICK scheme for the spatial discretization of the volume fraction. The 1st order implicit scheme was used for the transient formulation and Phase Coupled SIMPLE for pressure-velocity coupling.

An initial mesh sensitivity study reported in our previous work[39]for the same set-up revealed that a uniform mesh size of approximately 1.5 particle diameters is sufficient to guarantee mesh independence.This mesh size is well below the recommended 10 particle diameters[40]required to capture the main gas-solid flow structures.The interaction between the gas and solid phases was modeled using the Syamlal-O'Brien parametric model[41].The model is calibrated using experimental minimum fluidization conditions so that it predicts a drag force equivalent to the experimental drag force. The default viscous model in ANSYS Fluent 15 was adopted since in dense beds particleparticle collisions dominate and the gas-phase turbulence is negligible.

The velocity inlet and pressure outlet boundary conditions were specified at the bed inlet and outlet respectively meanwhile the partial slip of the Johnson and Jackson boundary condition[42]was imposed for the solid phase at the walls using phi values in the range of 0.5 to 0.005 for the three different superficial gas velocities while the gas phase was modeled using the no-slip boundary condition.

The simulations were initialized using the minimum fluidization condition and run for a total of 40 s on our Chemical Reaction Engineering (CRE) group Sugon I620r-G server consisting of 5 nodes each employing a maximum of 16 cores. Data sampling for time statistics was activated after 15 s at which the flow field achieved pseudo steady state as monitored from the pressure drop fluctuations and flux report of the mass flow rate at the inlet and outlet.“Numerical probes”wereset up within the computational domain at locations corresponding to the experimental set-up measurement positions to obtain time series data for pressure and solid particle velocity fluctuations sampled at a frequency of 200 Hz.

Table 2 Euler-granular model equations

4.Signal Analysis

In our study we have restricted the analyses to the time(standard deviation and correlation analyses)and frequency(discrete wavelet transform,spectral analysis,coherence)domain only as shown in Fig.3.The concepts in these analyses are derived in a very rigorous way in addition to the ease of application and reduced sensitivity to experimental noise in the data unlike the more advanced and complicated chaos methods[4].The standard deviation is a widely used time domain method to demarcate boundaries of regimes based on the changes in the amplitude of the signal while correlation analyses are useful for determining the relevant time scales in signals and changes in the time scales pertain to changes in the flow structures.Spectral analysis aims at studying the distribution of frequencies in a signal and identifying the so-called dominant frequency using the Fast Fourier Transform or FFT in short.In multiphase reactors such as bubble columns or fluidized beds dominant frequencies in the power spectrum are the frequencies at which bubbles/slugs pass through the bed.A change in the frequency distribution of the power spectra signifies a change in the flow regime.Spectral analysis using FFT suffers a setback in that information about the time scale is lost.To overcome this challenge the wavelet transform is employed which retains both the time and frequency domain information.Furthermore wavelet transform has a key feature of multiscale resolution which is useful for studying flow structures in multiphase reactors.

The experimental pressure signals originally sampled at 1000 Hz as aforementioned in Section 2 were resampled at a frequency of 200 Hz to match the sampling rate from the numerical predictions.The resampling was done using a resample subroutine in Matlab which applies an antialiasing low pass filter and compensation for the delay introduced by the filter.The different signal processing schemes shown in Fig.3 were then applied to the predicted and measured signals to identify regime change.

4.1.Standard deviation

The standard deviation,σ of a time series x(n)is the difference between instantaneous and mean of the particular series,i.e.the standard deviation of the distribution is expressed as[9]:

and n=1,2,3,···,N i.e.the number of samples used in the computation.

4.2.Autocorrelation function(ACF)

The normalized auto-correlation function,ACF in discrete form is given as[10]:

where τ is the time delay between successive data points in the series.

4.3.Cross correlation function(CCF)

The normalized cross correlation function is useful in studying the space-time flow characteristics of multiphase flow[43].For a bivariate time series of vertical signals x and y it is given in discrete form as:

similarly τ is the time delay.

Fig.3.Scheme of signal processing.

4.4.Spectral analysis

The power spectrum and the magnitude squared coherence function are estimated using the Welch method[9]without overlap between data segments available as subroutines in the Matlab environment.In this method the variance of the power spectrum is significantly reduced by estimating the spectra as an average of several sub-spectra.Furthermore the choice of the number of sub-spectra is realized as a compromise between frequency resolution and variance. The time series signal is divided into several segments usually in powers of 2 that is 256, 512, 1024, and 4096 and so on from which an estimate of the power spectrum of each segment is obtained.The averaged power spectrum is now given as:

where N is the number of segments and Pxxi(f)is the power spectrum estimate of each segment.

The coherence function describes the coupling between two different time series as a function of frequency and assumes values between zero and unity.A coherence value of unity implies that the two time series are completely coupled at a given frequency, f and on the other hand a coherence value of zero indicates that the pair of time series are completely uncoupled.Values in between zero and unity indicate a significant degree of coupling.The magnitude squared coherence is given as:

where Pxxand Pyyare the auto power spectra of signals x and y respectively and Pxyis the cross power spectrum.

4.5.Discrete wavelet transform(DWT)

The DWT of a sampled signal, x(n), involves filtering the signal into a low frequency component know as an approximation coefficient abbreviated A1 and a high frequency component known as a detail coefficient abbreviated as D1 using a pair of digital filters.Application of the inverse discrete wavelet transform(IWT)to A1 and D1 yields the original signal or the so-called reconstructed signal.This is the first scale decomposition and by repeating this procedure recursively up to a desired level j,a multi-scale resolution of the signal is realized which is represented as:

At each level of decomposition,the frequency range or band is given by:

where fsis the sampling frequency.It is worth noting the scale is inversely proportional to the frequency of the Fourier analysis.

The energy of the approximation coefficient,A at scale J and the detail coefficient,D at different scales is given as:

Total energy is given by:

The normalized energy at each scale is expressed as EAJ/E and EDj/E respectively.

5.Results and Discussion

The results are presented in four mainsections.Firstly the general fluidization behavior in terms of circulation patterns for the different operating conditions are presented and discussed.In the second and third sections,the results based on time and frequency domain analyses respectively are discussed and analyzed.Lastly correlations from the literature for predicting the onset of turbulent fluidization are compared with the fnidings from the experimental measurements and numerical predictions and the differences explained.

5.1.Visual observation of flow field

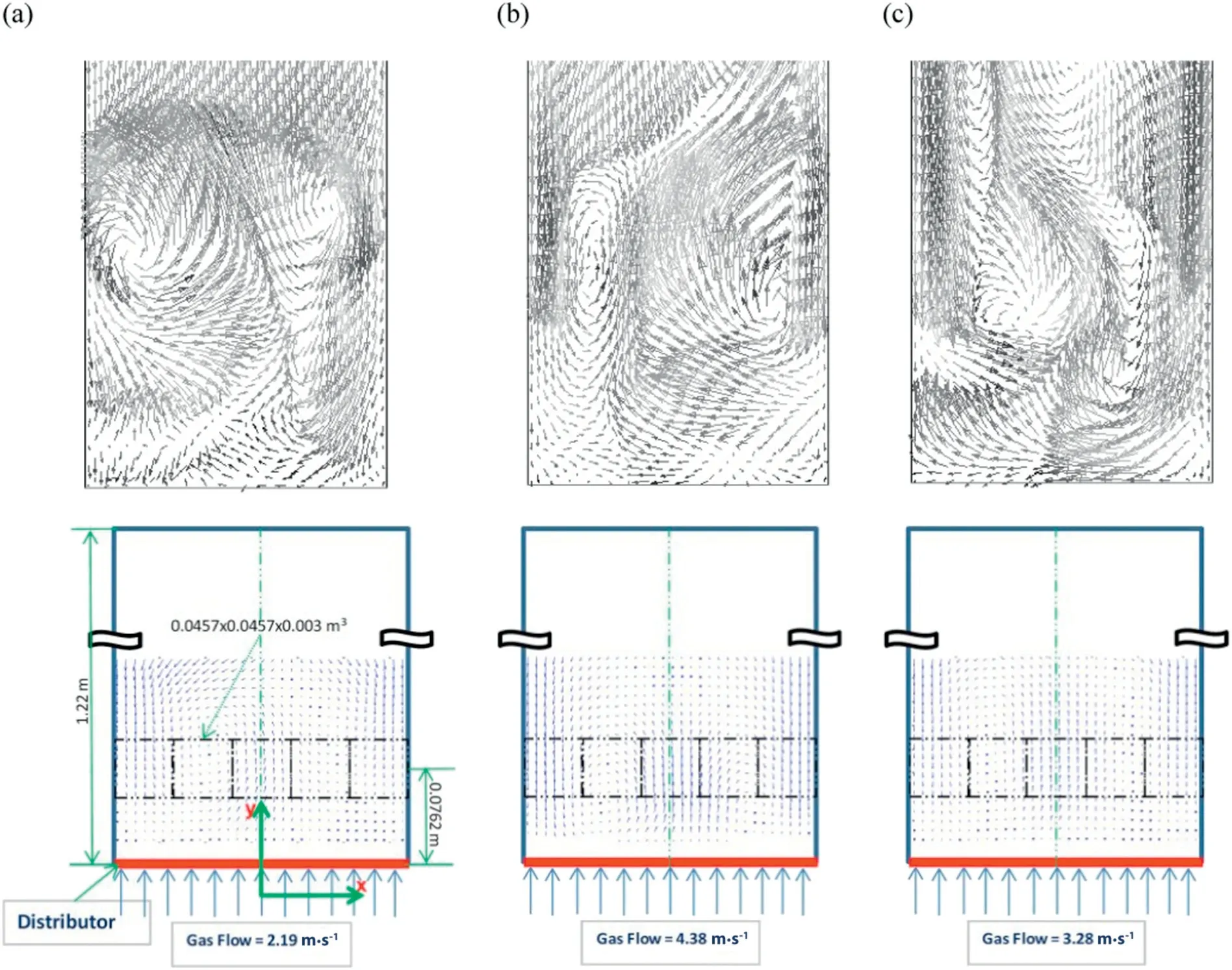
Fig.4.Comparison of predicted and experimental[35]solid mean velocity vectors at(a)Ug/Umf=2,(b)Ug/Umf=3 and(c)Ug/Umf=4.

The gross solid circulation patterns from TFM predictions and experimental measurements with HsPIV at different superficial gas velocities are compared in Fig.4.The experimental measurements using HsPIV make use of a high speed camera with a high resolution and frame rate.These gross circulation patterns are responsible for macro mixing in fluidized beds and have attracted a lot of attention from researchers over the years.Moreover the flow patterns are influenced by different operating conditions such as superficial gas velocity,bed aspect ratio,physical properties of the particles and type of gas distributor[44].A close inspection of the two sets of figures reveals a circulation pattern involving two main counter current rotating vertical structures which is typical for Geldart D particles [24] unlike other Geldart particle types which exhibit multi-circulation patterns.In this circulation pattern,the particles are carried up the center by rising slugs and voids to the surface of the bed and upon bursting of the slugs and voids,the particles fall down along the walls under the influence of gravity.From the numerical predictions it can also be observed that with increasing superficial gas velocity,an increased amount of particles is pushed near the walls and the gross structures increase in size thereby increasing the contact between phases and improving the mixing ability of the bed.Contour plots of mean solid concentration(not shown here but available on demand) show a somewhat increasingly core-annular structure with increasing superficial velocity.In summary we can safely say that the numerical predictions predict the correct solid circulation pattern observed from the experiments.

5.2.Methods based on time domain analysis

A comparison of predicted and measured differential pressure drop time series for different operating conditions is depicted in Fig. 5. A time series plot for a given quantity of interest gives a qualitative description of the time scales and complexity of the flow structures at a first glance[9].For gas-solid fluidization systems,dominant frequencies are in the range of 1-5 Hz and therefore 10 s is deemed sufficient for such plots.In comparison to the predicted signals,the measured fluctuations are noisy due to the high sampling rates. Moreover pressure fluctuations originate from different sources including bubble passage,bubble generation,bubble coalescence,bubble eruptions and gas flow fluctuations which might not all be well replicated by the model which might explain the slight differences between model predictions and experimental measurements. It is worth noting that in the CFD simulations the pressure fluctuations were monitored at the two heights(absolute pressure)and the differential pressure was obtained as the difference between the two whereas in the experimental measurements,the differential pressure between the two positions was obtained directly by the Setra differential pressure transducer as aforementioned.The time behavior of the two sets of signals has strong resemblance but further quantitative analysis is needed in order to extract meaningful information.The strong periodicity which is more pronounced for the experimental measurements is typical of slugging fluidization due to the passage of voids and slugs unlike bubbling fluidization which is characterized by multitudes of bubbles and therefore lacking a clearly visible periodicity.From visual inspection at Ug/Umf=4,the frequency of the fluctuations seemly reduces indicating a regime change.

Fig.6 displays the variation of the standard deviation with Ug/Umf.The higher amplitude of the predicted fluctuations is a reflection of the larger bubbles predicted by the CFD simulations.With an increase in the superficial gas velocity, that is Ug/Umf= 3, a corresponding increase in the amplitude of the predicted and measured fluctuations is observed however the magnitude of the measured fluctuations is larger this time around.This is expected since more gas flows through the bed in form of slugs and/or bubbles leading to larger amplitudes.At Ug/Umf=4,a decrease in the amplitude of the pressure fluctuations is observed.It can be observed however that the decrease in the measured fluctuations is more pronounced.The decrease in the amplitude signals the transition from a slugging regime to a turbulent regime.

Fig.5.Time series of predicted and measured pressure fluctuations for(a)Ug/Umf=2,(b)Ug/Umf=3 and(c)Ug/Umf=4.The fluctuations were obtained between 0.0413 and 0.3461 m above the distributor.

Fig.6.Standard deviation of predicted and measured differential pressure fluctuations as a function of the dime.

Although CFD predicts the regime transition qualitatively well,the quantitative agreement with the experiments is not as good.The difference is attributed to the inadequacy of the TFM in modeling the particle-particle, particle-wall and gas-solid interactions. In our recent work based on the same experimental setup[45],the pressure fluctuations showed significant sensitivity to the specularity coefficient used.The coefficient quantifies the friction between and the solid particles and the wall. An increase in the amplitude of the fluctuations was observed with decreasing particle-wall friction.The specularity coefficient value used in this work is the optimum value arrived at after testing several different values.

Fig. 7a and b displays the autocorrelation function,ACF for predicted and measured pressure drop fluctuations respectively at three different superficial gas velocities.Once again the qualitative agreement between the predictions and the experiments is satisfactory.Both plots show that the periodicity of the fluctuations passes through a maximum at Ug/Umf=3 which is consistent with the observations from Fig.6.An increase in Ug/Umfto 3 translates into increased bubble/slug motion. Different authors have used different criteria to estimate the characteristic time scale from the ACF plots,in this work we consider first peak after τ = 0 to characterize the fluctuation period (reciprocal of the time shift) following Clark et al.[46].From Table 3 it can be concluded that both numerical predictions and experimental measurements yield similar time scales and that at Ug/Umf= 3, a transition from slugging to turbulent flow takes place. Nonetheless there are clear observable differences between the numerical predictions and experimental measurements.The ACF of the measured pressure fluctuations decays slower in comparison to the ACF of the predicted fluctuations in other words it exhibits stronger correlation. As aforementioned particle-particle,particle-wall and gas-solid interactions in the TFM significantly affects predicted fluidized bed dynamics and this might explain the differences between the shapes of the predicted and simulated pressure drop ACF.

Fig.7.Autocorrelation function for(a)predicted and(b)measured pressure fluctuations at different fluidization numbers.

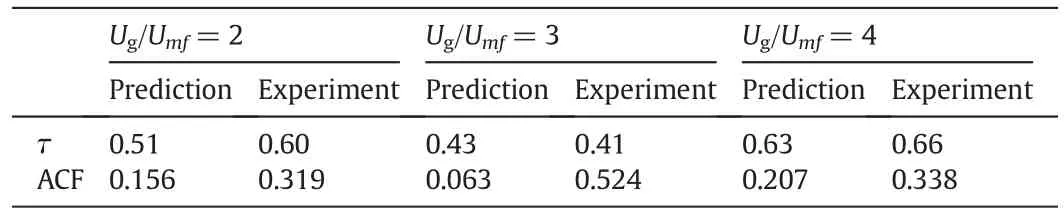
Table 3 Predicted and experimental time lags and autocorrelation coefficients for different operating conditions

The overprediction of the gas-solid interaction in the simulations is evident from the predicted suspension densities i.e.ρα]at different superficial gas velocities.Higher suspension densities translate to reduced particle-particle collisions which perhaps might explain why the ACF from the CFD predictions decays faster in comparison to the ACF from the experiments.The particle-particle coefficient of restitution which characterizes the particle-particle interactions was specified as part of the problem by NETL and therefore no parametric study for this quantity was done.Goldschmidt et al.[47]have previously shown that the intensity of the pressure fluctuations in a fluidized bed decreases with increasing coefficient of restitution.It means that as the collisions become increasingly elastic,the intensity of the fluctuations reduces.In another study,Godfroy and co-workers[48]observed that the ACF became stronger(slow decay)with reducing solid circulation in a gas-solid riser due to reduced particle-particle interactions.It is therefore likely that by adjusting the particle-particle coefficient of restitution in the simulations, the predicted ACF can be matched to the ACF from the experimental measurements.

Fig.8.Cross correlation function(xcf)from predicted pressure fluctuations at probes located at heights of 0.0413 m and 0.3461 m above the gas distributor for different fluidization numbers.

Fig.9.Comparison of PSD of(a)predicted and(b)measured differential pressure drop fluctuations for different operating conditions.

The cross correlation measures the similarity between the reference signal x and shifted copies of signal y as function of the time shift.The time shift at which the maximum correlation coefficient occurs is representative of the dominant slug rise velocity[46].Fig.8 shows the cross correlation coefficient computed from predicted absolute pressure signals at vertical distances of 0.0413 m and 0.3461 m above the gas distributor for different operating conditions.Comparisons with experimental results are not possible because the signals were acquired as differential pressure signals between the two ports in the experimental set-up whereas in the simulations we acquired both absolute and differential pressure signals.The peak cross correlation coefficients for Ug/Umf=2,3 and 4 are 0.241,0.467 and 0.456 respectively.It can be seen that the correlation coefficient peaks at Ug/Umf=3 reinforcing the conclusion that this condition signifies a regime change from slugging to turbulent. Fan et al. [49] computed the rise velocities of bubbles, slugs and pressure waveform using the cross correlation method.The average velocity of the bubble,slug or pressure wave was computed by dividing the known distance between two vertically placed pressure probes with the time delay i.e.maximum cross correlation coefficient.A decrease in the slug velocity was observed during the transition from slugging to turbulent flow.Furthermore Bi and Grace[3]observed that the plot of the maximum cross correlation coefficient versus superficial gas velocity peaked at a value quite close to the value from the standard deviation method.Our observations from the numerical simulations are therefore consistent with observations from previous experimental research work.

5.3.Methods based on frequency analysis

A comparison of the predicted and measured pressure fluctuation normalized PSD at different operating conditions is shown in Fig.9.A total of 4096 samples from the numerical simulations were used for the Welch estimation of the PSD.Meanwhile fluctuations from the experimental measurements were resampled at 200 Hz to match the sampling from the simulations and 32768 resampled data points were used for the estimation of the PSD.For each sub-spectrum(CFD and experimental measurements),512 samples were used giving an average of 8 spectra for CFD simulations and 64 spectra for experimental measurements.For this number of sub-spectra samples,a frequency resolution of 0.3906 Hz was realized.It is worth mentioning that the same number of sub-spectra samples was used for the computation of the magnitude squared coherence function.Comparing the two sets of spectra,it can be observed that at low frequencies characterizing the macro and meso flow structures,the agreement between the numerical predictions and the experimental measurements is excellent.The fundamental or dominant frequencies from the PSD plots which represent the passage of bubbles/slugs in the bed are reported in Table 4.The dominant frequencies from both the numerical simulations and experimental measurements go through a maximum with increasing superficial gas velocitysignifying a change in the flow regime from slugging to bubbling.During regime transition there is a significant change in the frequency distribution[9].In the power fall off regions of the spectra i.e.at frequencies greater than 5 Hz,the shapes of the two sets of spectra are different and this can be attributed to the different number of samples and spectra averaged[9].Another reason might be due to the complex individual particle behavior in the micro scale which is not accurately captured by the numerical simulations as aforementioned.Another noteworthy observation is that the shape of the respective sets of the PSD plots from the predictions and measurements is hardly affected by the change in the operating conditions which is consistent with the findings of van der Schaaf et al.[17].For the purpose of identifying regime change,the PSD tool is sufficient because the phenomenon of interest that is the bubble behavior is at the low frequencies.

Table 4 Comparison of dominant frequency from PSD plots in Hz

The magnitude squared coherence between measurement positions 0.0413-0.3461 m is displayed in Fig.10 for different superficial gas velocities.Coherent phenomena include bubble coalescence,gas flow fluctuations,bubble eruption and bed mass oscillation which generate a global pressure wave whereas the incoherent phenomena includes gas bubbles, clusters and turbulence which are localized [50]. It can be seen from the figure that the coherence peaks at low frequencies(0-2.5 Hz) for all the operating conditions and is relatively low for the most of the frequency range under consideration.At this measurement position, the slugs have changed in size, shape and velocity thus exhibiting low coherence at most frequencies with the exception of the global flow structures at low frequencies.In general the coherence increases with decreasing distance between the measurement positions and vice versa[50].The peak in the coherence function is also reflected in the PSD representing the dominant frequency.A closer inspection of the plot shows that the coherent power is different for different superficial gas velocities.Using the coherence function,Ellis[51]detected the flow regime transition from bubbling to turbulent fluidization.

Fig.10.Coherence for measurement position 0.0413-0.3461 m above the plate distributor and for different operating conditions.

Cai et al.[52]defined an average coherence functionγ2xy（f）df where f1and f2are 0 and 10 Hz respectively.This frequency range is typical of major frequency content in fluidization systems which is typically below 10 Hz[11]and closely linked to bubbling motion.Plotting the average coherence function as a function of superficial gas velocity,a peak is observed at the transition velocity from bubbling/slugging to turbulent fluidization[51-53].This observation can be explained by exploring further the concept of coherent and incoherent phenomena.The coherence between the plenum chamber or inlet position and measurement positions within the bed discriminates between fast moving waves(high coherence)and gas void motion(low coherence). At low superficial gas velocities, the propagation of pressure waves due to the local passage of gas voids is low of order of the bubble rise velocity in comparison to that of other sources which is of the order 10 m·s-1and the latter are therefore filtered out leaving the local gas void information. With the increase of the superficial gas velocity,there is now a corresponding increase in the pressure waves due to gas voids in addition to the fast traveling waves leading to an increase in the average coherence up to the transition point.Beyond the superficial velocity at the transition point(turbulent regime),the average coherence begins to reduce because the voids and slugs have reached their maximum diameter and are now splitting up contributing to the attenuation of the pressure waves ultimately leading to a reduction in the average coherence.In the present workfor Ug/Umf=2,3 and 4 was computed to be 0.1565,0.2332 and 0.1420 respectively.The result from the CFD simulations is consistent with the previous experimental findings[51-53]demonstrating that the average coherence is a reliable tool or method for detecting regime change in gas-solid fluidized beds by observing the changes in the characteristic length scales of the voids with changing operation or physical parameters.

The coherence function has been previously utilized to decouple pressure fluctuations in gas-solid fluidized beds[50,54]and slurry bubble columns[55,56]into coherent and incoherent components.Coherent phenomena include bubble coalescence, gas flow fluctuations,bubble eruption and bed mass oscillation which generate a global pressure wave whereas the incoherent phenomena include gas bubbles,clusters and turbulence which are localized. The coherent output power,COPxyand incoherent output power,IOPxyexpressed as a function of the magnitude squared coherence are given as[50]:xy

and

respectively.

In accordance with Parseval's theorem,the areas under the PSD versus frequency curves of COPxyand IOPxyare equivalent to their respective variances i.e.

Eqs. (14) and (15) were solved with numerical integration in Matlab®yielding the respective variances from which the standard deviations were computed. The PSDs of absolute pressure fluctuations(APF),differential pressure fluctuations(DPF),incoherent power output,IOPxyand coherent power output,COPxyof the predicted pressure fluctuations at different operating conditions are presented in Fig.11.The PSDs from the absolute and differential pressure fluctuations overlap for all the operating conditions as can be observed from the figure.Differential pressure fluctuations ideally filter out fluctuations from other locations thus giving local information and strongly depend on the probe spacing.In this study the differential pressure was measured across the entire bed i.e. 0.0413-0.3461 m which explains why they overlap with the absolute pressure fluctuations.Essentially the information recorded by DPF is the same as APF due to the large spacing of the probes and negligible filtering.It can also be interpreted from the figure that the power of the decoupled pressure fluctuations is lower in comparison to the power of the APF and the DPF for all operating conditions.Another noteworthy observation is the reduction in the difference between the APF/DPF with IOP power spectra with increasing superficial gas velocity.This is due to the increase in the power of the incoherent output power due to local phenomena i.e.bubble motion with increasing superficial gas velocity.This is also reflected by the increasing standard deviation with superficial gas velocity.

At low frequencies and for all operating conditions,a peak around 2 Hz can be observed from the PSD of the COP as opposed to the PSD of the IOP representing large scale oscillations or gravity waves. As aforementioned, the IOP represents localized events while the COP component represents global events. This dominant low frequency component can also be readily seen from the plot of the coherence function versus frequency in Fig.11 representing the gross circulation patterns.The peaks are not readily identified on the spectral plots of the IOP due to the wide distribution of power as a result of the bubble motion[11].

The amplitude of the different signals at different operating conditions expressed as the standard deviation is presented in Table 5.The magnitudes of the absolute and differential pressure fluctuations are in close proximity and therefore reinforce the observations from Fig. 11. Moreover a maximum is observed at Ug/Umf= 3 which is interpreted as regime change.As for the IOP and COP,their respective magnitudes increase with increasing superficial gas velocity and no maximum is observed as reported earlier by Zhang et al.[57]for a pseudo 2D bed with Geldart A particles.The operating conditions in their work covered the bubbling and turbulent regime and therefore the maxima in the standard deviation of the IOP could be taken as an indicator of regime change similar to the differential pressure fluctuations.From the table it can also be seen that the amplitude of the IOP fluctuations is larger than the amplitude of the COP for all operating conditions.This is expected due to the slugging nature of the flow.The IOP in this case is representative of the slugging motion.In addition attenuation of the pressure/sound waves which constitutes the COP is significant due to the large probe spacing across the bed.

Fig.11.Comparison of spectral densities of absolute pressure fluctuations,differential pressure fluctuations,incoherent output power and coherent power output for(a)Ug/Umf=2,(b)Ug/Umf=3 and(c)Ug/Umf=4.

Table 5 Standard deviation,σ(Pa)for APF,DPF,IOP and COP at different operating conditions

Fluidized beds like other multiphase reactors exhibit multi-scale structures which affects its overall performance.Three principal scales are identified in fluidized beds,that is the microscale associated with noise or individual particles,meso scale associated with clusters/bubbles/slugs and macro scale associated with the equipment[58,59].Unlike the previous methods used for studying regime change we now employ a multi-scale resolution approach using the discrete wavelet transform,DWT.In the present work a 12 scale discrete wavelet transform(DWT)was applied to the predicted and measured pressure fluctuation signals at different operating conditions.The frequency bands of the 12 scale decomposition are shown in Table 6.

The normalized wavelet energy has been previously shown to be sensitive to fluidized bed operating conditions[60,61]and is therefore adopted in this study for detecting regime change.Fig.12 shows the normalized wavelet energy plots of the predicted and measured pressure drop fluctuations at the three superficial velocities.The profile of the wavelet energy from the TFM and experimental measurements is remarkably similar demonstrating the capability of CFD to model the complex multiscale flow structures.The energy from the numerical predictions and experimental measurements is relatively low at scales D9-D12 and then sharply increases peaking at scale D6 and then starts decreasing again leveling off at scale D3. Therefore D8 delineates the boundary between the macro and meso scales whereas D3 forms the boundary between the meso and micro scales.The three principal scales are thus designated as D1-D3 for the microscale representing particle interaction,D4-D8 for the mesoscale representing the gas voids and slugs and D9-D12 for the macroscale representing the effect of the equipment. It can be observed from the figure that the majority of the energy content lies within the meso-scale which is consistent with the findings of Zhao and Yang[59].The peak in the energy profile at D6 is representative of the dominant frequencies of the system already seen from the PSD and magnitude squared coherence function plots.

Table 6 Frequency bands of the 12 scale wavelet decomposition of signal sampled at 200 Hz

Fig.12.Normalized wavelet energy plot for(a)predicted and(b)measured pressure fluctuations at different operating conditions.

Using these three scales as a basis,a comparison of the normalized energy is done and reported in Table 7.It can be seen that the bulk of the total energy, ＞90% is concentrated in the meso scales in bold while the remainder is distributed between the macro and micro scales.From the table it is observed that during the transition from slugging to turbulent flow at Ug/Umf=3,the energy is maximum while it is lower in the slugging and turbulent regimes.During the transition from slugging to turbulent flow the predominant mechanism changes from bubble/slug coalescence to bubble/slug splitting[52]and the competing effects of these two mechanisms leads to the increase of the energy of the meso-scale structures.

5.4.Comparison of literature correlation for the transition velocity

Several authors have proposed correlations for the prediction of the transition velocities in the open literature.Bi et al.[62]have given a summary of the equations some of which have been adopted in this study and shown in Table 8 together with predicted values of Uc.Most correlations have the general form of Rec=aArbwhere Rec=ρgUcds/μgand Ar=ρg(ρs-ρg)ds3g/μg2.For the physical and system properties in Table 1, the Ar is equal to 1172237. In comparison to the results from the experimental measurements and CFD predictions,the correlations from the literature overpredict Ucand show wide scatter with relative errors ranging from 37.44% to 96%. This is not surprising since these correlations are empirical and are therefore limited in their prediction capabilities. Moreover, the correlations from literature are based on systems with different physical properties, measurement techniques and experimental conditions,all of which contribute to the wide scatter and limited prediction.In the absence of a unifying theory for describing the transition from bubbling/slugging to turbulent,CFD seems to be a very attractive approach to tackling this challenge and this work is a first step in adopting computational methods for detailed studies of regime transition.

6.Conclusions

In this work the flow transition from slugging to turbulent was studied by means of numerical simulations using the TFM approach.Absolute and differential pressure fluctuations from the numerical simulations and experimental measurements were analyzed usingtime and frequency analysis methods in order to detect the transition velocity,Ucfrom slugging to turbulent flow and to characterize the regime change.The qualitative agreement between the results from numerical predictions and experimental measurements was quite good.Quantitative differences could however be noticed due to the inadequacy of the model to accurately capture the gas-solid,particle-particle and particle-wall interactions.For the system under consideration,correlations from the literature failed to predict the transition velocities with relative errors ranging from 37%to 96%.Moreover the values of Ucfrom the correlations show a wide scatter due to the large amount of empiricism in their derivation. Going forward, CFD shows great promise in characterization of fluidization regimes in comparison to experiments,a good number which are expensive to set up and have limited practical applications.

Table 7 Normalized energy distribution for multi-scale pressure fluctuation signals

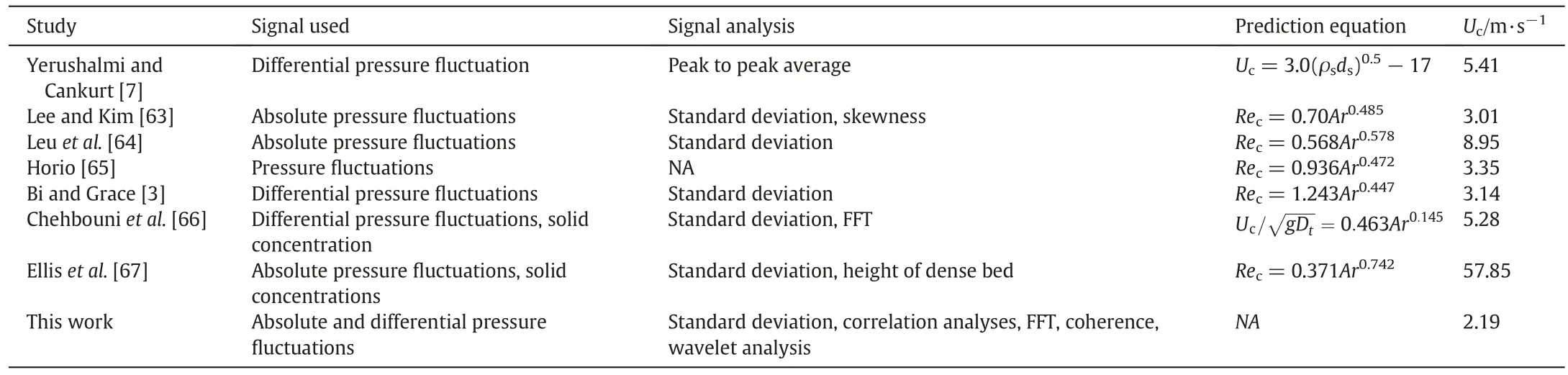
Table 8 Literature correlations for transition velocity,Uc

Nomenclature

Ar Archimedes number

E normalized wavelet energy

e particle-particle restitution coefficient

f frequency,Hz

g acceleration due to gravity,m·s-2

g0 radial distribution function

H bed height,m

P pressure,Pa

Res particle Reynolds number

Rec particle Reynolds number at regime transition

t time,s

U superficial gas velocity,m·s-1

x time series of parameter of interest

α volume fraction

αs,max packing limit

βgs gas/solid momentum exchange coefficient,kg·m-2·s-1

γs collisional energy dissipation,J·m-3·s-1

θ,Θ granular temperature,m2·s-2

λs bulk viscosity,Pa·s

μ viscosity,Pa·s

ρ density,kg·m-3

τk stress tensor of phase k,Pa

Subscripts

g gas

mf minimum fluidization

s solid

x lateral coordinate

y vertical coordinate

Acknowledgments

The authors would like to thank Dr.Balaji Gopalan of National Energy Technology Laboratory for providing the additional data and for attending to our queries.