水库入库流量锯齿状波动问题探讨

周 栋

（湖北省咸宁市水文水资源勘测局，湖北 咸宁 437100）

0 引言

水文预报中，在洪水来临时，需要监控水库各时段的实际入库过程，即从起涨～峰顶～落平任意时刻的入库流量。入库流量的特性注定了其不能直接实测得到，只能靠实测部分推算或则全部推算得到。综合国内外的推求方法，根据各水库水文资料的详实程度，目前入库洪水计算方法主要有流量叠加法、流量反演法、水量平衡法及相应关系法等。水量平衡法由于其概念清晰，计算简便，仅需记录各时刻的库水位，再根据水量平衡原理及水位库容曲线，反推得到入库流量，此种方法简便易操作，且具有较高的精度，满足水库日常运行的要求，为较多数的水库所采纳[1]。

1 入库流量计算原理

水量平衡原理的方程表示如下：

式中：Δt 表示时段长度，Qt为时段平均入库流量，qt为时段平均出库流量，Wt、Wt+1分别为时段始末的蓄水量，整个公式可理解为单位时间内，入库流量在数值上等于出库流量加上时段内蓄水量的变化量。出库流量一般包括有发电流量、下泄流量及蒸散发量，机组发电流量可查机组H-N-Q 曲线得到，泄水建筑物的下泄流量可查闸门的H-q 曲线得到，单位时段内水库蒸散发量及渗漏量由于数量值较小可忽略不计，由此可见时段内的出库流量可较准确的测量。水库蓄水量的变化ΔW=Wt+1-Wt是指时段末、初水库蓄水量相减，而时段初末水库蓄水量一般又是根据时段初、末坝前水位查水位库容关系曲线得到。最后确定计算时段，求出ΔW/Δt，与qt累加得到初步的入库流量过程[2]。

2 入库流量锯齿状波动原因分析

入库流量计算过程中产生误差的因素较多，虽然水量平衡法是由物理学上的质量守恒定律推导而来，各类水的总量保持不变。但是，在水量平衡原理各值的求解过程中，由水位推算库容，由水头推算发电流量等，多个涉及到计算的数据都是由观测值经过各类曲线线性内插得到，不是直接观测得到的，在推算过程中就无可避免的会产生各类不可预计的误差。

出库流量，水库单位时段内的出库流量一般包括时段的发电流量、泄水建筑物的时段下泄流量、水库渗漏量与蒸散发量，兼具通航用途的水库存在通航消耗的流量，兼具灌溉、生活供水功能的水库存在灌溉用水及生活引水量。上述这些流量除渗漏量和蒸发量外，其他流量都是可以准确测量的，而时段内的蒸发量和渗漏量在数值上较小，与其他流量不在一个数量级，完全可以忽略不计。因此，水电站的出库流量是可以精确得到的，这一过程不会产生过大的误差[3]。

蓄水量变化值，时段内蓄水量的变化值是由时段末蓄水量减去时段初蓄水量得到，而时段初、末的水库蓄水量一般又是根据时段初、末坝前水位查水位库容关系曲线线性内插得到。由水位推算库容这一过程极易出现误差，主要表现在两个方面：一是坝前水位的代表性不够，坝前水位不能代表库区的平均水位；二是水位读取的精度不足。现实中的水库在坝前水面线不是绝对水平的，一般会在坝前呈现跌水或壅水的现象。蓄水的时候坝前出现壅水现象，泄水的时候坝前出现跌水现象，因此，水库的坝前水位与库区的平均水位二者并不能等效替换，坝前水位并不能代表整个水库的平均水位。以水电站开闸泄水、闭闸蓄水两种情况为例，对这两种情形下的库区水面线情况进行分析，得到的分析结果如下。水库开闸泄水的水面线情况见图1，首先定义时段初和时段末两个时段，时段初坝前水位在D 点位置，此时库区实际水面线为ACD，时段末由于闸门泄水的缘故，库区在坝前上游位置上出现明显的水跌现象，水位跌到了F 点位置，此时库区实际水面线为ACF，这是实际上的情况。但是在计算的时候，目前计算时段水库蓄水量时，采取的方法都是直接将坝前水位视为水库的平均水位，时段末水位对应的库容为EFG 包围的区域，时段初水位对应的库容为BDG 包围的区域，二者相减得到时段蓄水量的变化即为BCFE 包围的库容。而实际上时段蓄水量的变化为CDF 包围的库容，实际蓄洪量小于计算所得的数值，由于EFG 对应的库容小于BDG 的对应库容，所以时段水库供蓄量ΔV 是个负值，故会使计算得到入库流量偏小。这种算法基于一个前提假设，即水库坝前的水面线是水平的，坝前水位就代表着整个库区的平均水位。而在实际的情形下，库区坝前一段的水面线并不是完全水平的，特别是在一些狭窄的河道水库，沿程水面线变化较大，坝前水位不能代表水库的平均水位。由于水位是下降的，时段初库容ΔV 在数值是负的，所以ΔV/Δt 数值也是负的，因此叠加出库流量后会使得计算的入库流量值偏小。当ΔV/Δt 的绝对值大于出库流量值时，入库流量的计算值就是个负值，这就是反推得到的入库流量会出现一些负值的原因所在。

闸门关闭的情况与闸门开启的情况相反，水库闭闸蓄水坝前的水面线情况见图2，时段初坝前水位在F 点，实际对应的水库水面线是曲线AEF，而不是虚线DF；时段末坝前水位在C 点，对应的实际库区水面线为曲线AEC，而不是虚线BC。因此，实际的时段供蓄量为CEF 包围的库容，而不是BCDF 包围的库容，由于两库容变化均为正值，会使得计算的供蓄量比实际的放大了很多倍，叠加出库流量后致使计算的入库流量值偏大。

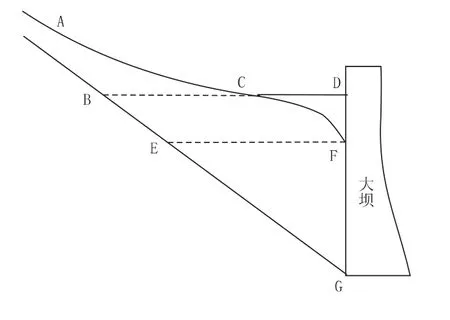
图1 开闸泄水坝址水面线图

图2 闭闸蓄水坝址水面线图

结合上述论证分析总结可得，入库流量呈现锯齿状波动的原因主要有：动库容原因、水位波动影响、水位库容关系曲线、机组H-N-Q 曲线等建立之初就存在的系统误差、时段长度的选取等。

动库容的影响：动库容是指水库库区回水水面与坝前水位水平面之间的楔形水库的容积，由上述开闸闭闸的情况分析可知，由于受到动库容的影响，水库的坝前水位并不能代表水库的平均水位，尤其是闸门启闭过程中，会使坝上游水面线急剧变化，开闸蓄水量减少，调节库容为负值，其数值偏大致使计算得到入库流量偏小；而闭闸时情况则相反，此时会在在库区坝前形成壅水的现象，使得计算得到入库流量偏大。对于动库容比较大的水电站，动库容是入库流量呈现锯齿状波动起伏的主要原因[4]。

水位波动的影响：由于受机组发电、闸门启闭、风向、航船等的外在干扰，坝前的水位值本身就存在着上下不规则的波动，进而直接影响到入库流量的推求。与此同时，坝上用于监测的水位传感器的精度及读取数据时产生的误差影响作用也较大，一些水位传感器的精度已经可精确读数至0.001 cm。但是据了解，目前大多水库、水电站在读取记录水位数据时，通常只记录到0.01 m 也就是整cm 的级别，而从反推入库流量的角度上来看，时段前后1 cm 的水位变化反推得到的库容变化是十分巨大的，以浙江衢州湖南镇水库为例，1 cm 水位对应的流量变化大约是90 m3/s，由此推算产生的流量误差高达几十立方米每秒。以湖南镇水库为例，情形一：某一天8 点整，传感器水位为216.2749 m，记录时直接取216.27 m，9 点传感器水位为216.2753 m，记录时取216.28 m，实际上8 点到9 点水位的变化只有0.0004 m，但是计算的时候时段水位变化取的是0.01 m。情形二：某一天8 点，传感器水位为216.2700 m，记录时直接取216.27 m，9 点传感器水位为216.2749 m，记录时取216.27 m，实际上8 点到9 点水位的变化足有0.0049 m，但是计算的时候水位按等值进行处理，由此反推得到的入库流量误差会更大。很多情况下，由于上述这两种情形由四舍五入而导致的误差影响极大，采集到的水位不能真实反映实际水位的变化趋势，由此递推得到的入库流量也就存在很大的偏差。

曲线误差：在反推入库流量的计算过程中，需要根据记录得到的水位通过水库的水位～库容关系曲线来计算得到相应库容。一旦水库初始建立的水位～库容关系曲线本身就存在误差，就会导致后续计算得到的库容变化不准确，使得反推得到的入库流量不准确，使得流量序列出现锯齿状波动起伏。同理，在出库流量的计算中，需要应用到电站闸门的H-q 曲线和各台机组的H-N-Q 曲线，这两种曲线同样在建立之初可能就存在系统误差，使得出库流量计算不准确，最终影响到入库流量的推求上来。

时段长度影响：由于出库流量与水位在不同时间段其变化是不一致的，故水量平衡公式中时段Δt 的长短对各变量的影响程度也是不同的。例如当负荷变化得较为频繁时，则计算时段应该短些，才能反映出机组负荷的实时变化情况，准确计算出发电流量；而当水位的跳变较频繁或剧烈波动时，则计算时段应稍微取长一点，避免受到水位急剧变化而导致水位的读数不具代表性。

3 结论及建议

本文针对水库入库流量锯齿状波动的问题，基于入库流量计算原理对数据波动的原因进行探讨，得出：流量锯齿状波动的主因是动库容的影响，其次是水位波动及读取数据的影响，闸门的H-q 曲线和各台机组的H-N-Q 曲线的影响。而由于动库容是计算原理上存在的系统误差，水位的波动不可避免，解决锯齿状波动的问题可以从数据的角度出发，运用线性平滑的方法对入库流量进行修正。查阅相关文献可用最小二乘法求解得到五点三次线性平滑方程[5]，再对入库流量进行线性平滑处理。图3、图4 为南方某水库入库流量运用五点三次算法进行平滑处理的结果，由图可知，平滑后的流量数据走势与原始数据基本相同，且洪水总量、洪峰流量与峰现时间洪水三要素与原始数据差异较小，能够较好的拟合原始流量数据，具有较高的实际应用价值。

图3 某单峰场次洪水五点三次线性平滑结果对比图

图4 某复式峰场次洪水五点三次线性平滑结果对比图