羽毛球拍网面振动的理论与仿真分析

林 青,严舒芯,程 磊

(1.南京林业大学 体育部，江苏南京 210037；2.南京林业大学 机械电子工程学院，江苏南京 210037)

随着国民经济的迅速增长，人民生活水平不断提高，体育活动越来越受到人们的青睐，尤其羽毛球运动普及较广，成为老少皆宜的运动形式。出于对羽毛球运动的喜爱，人们对羽毛球球拍的选择越来越重视，在球拍的研发过程中, 不仅需要综合考虑球拍的重量、平衡、硬度、弹性等重要因素,尤其需要研究球拍网面的性能[1]。本文运用膜振动理论和有限元分析方法对羽毛球拍网面的性能进行分析，以期为专业运动员了解拍面性能，发挥球拍的最佳效果以提高运动效率提供理论依据。

1. 羽毛球拍网面的理论分析

1.1 膜振动理论

膜结构是20世纪70年代发展起来的一种新型的张力结构形式，它具有刚度小、重量轻等特点，膜振动就如同鼓上的鼓皮在敲击下产生振动一样[2-4]。进行圆膜的振动理论分析时，首先，在直角坐标下，通过受力分析以及牛顿第二定律建立膜振动的平衡方程；其次，考虑到在直角坐标下的方程求解比较复杂，可将其化成在极坐标下的圆膜振动方程，利用分离变量法将方程转换成零阶贝塞尔方程标准式，通过求解得到圆膜的位移表达式；然后，通过施加圆膜的边界条件推导出圆膜简正频率方程，计算出各阶的频率。

设一张紧的膜处于xy平面上，在膜上取一个曲边四边形，膜四边所受的力称张力记为T，单位为N/m。

假设当膜受到与xoy面相垂直方向的外力作用后，在张力T的作用下，产生垂直方向的振动。面单元dxdy在横向振动时，膜边缘都受到张力的作用，张力与膜的切线方向一致，张力T与x轴的夹角为β，张力T与y轴的夹角为α。根据牛顿定律，作用在面单元dxdy的外力和膜振动时产生的惯性力的合力应等于零。面单元在直角坐标系的受力分析图如下(图1)。

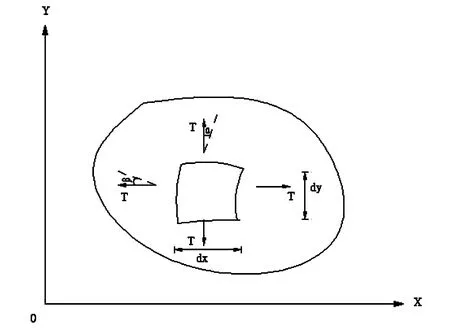
图1 直角坐标系面单元受力图

因此可解得作用于面单元四个边缘的净力合力为

(1-1)

设σ为面密度，则面单元的质量为

dm=σdxdy

(1-2)

面单元振动的加速度为

(1-3)

根据牛顿第二定律得

F合=dm·a

(1-4)

(1-5)

1.2 羽毛球拍面膜振动的方程

羽毛球拍面近似为椭圆形且为网状结构，本文将羽毛球拍面近似看成圆形膜且击球时视为膜振动。由于上式膜振动方程是在xoy坐标下的拉普拉斯方程，求解比较复杂，所以一般将其变换成在极坐标下进行求解[5-6]。

(1-6)

式1-6中θ—极角，r—极径。极坐标下膜振动的微分方程为

(1-7)

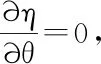
(1-8)

选用复数的形式[7]，即令T(t)=ejωt并利用欧拉公式带入1-8得

(1-9)

此方程式为零阶贝塞尔方程的标准式[8]。其有零阶贝塞尔函数和零阶诺依曼函数两个特解，所以该方程的一般解是两个函数的线性组合即

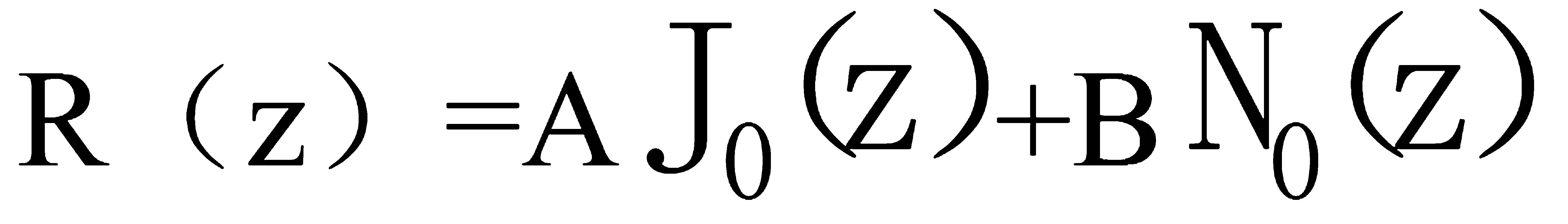
(1-10)

所以1-9变为

(1-11)

考虑到诺依曼函数具有一个在零点发散的特性，即当r=0时，N0(0)→∞。对于具有张力的圆形膜而言，在圆心r=0处的振动是有限的，则必须要求上式B=0，因此，1-10方程解为

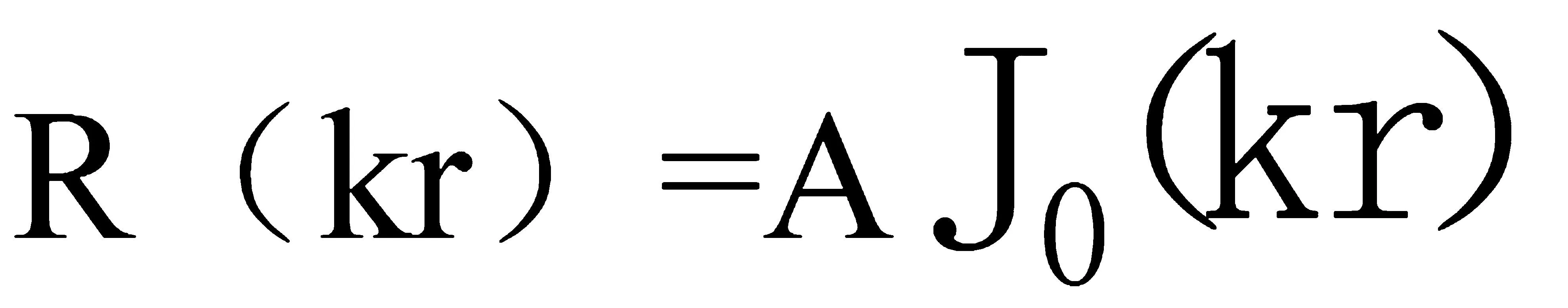
(1-12)

则膜的位移可表示为

(1-13)

将1-13方程变量换成x，得到贝塞尔方程为

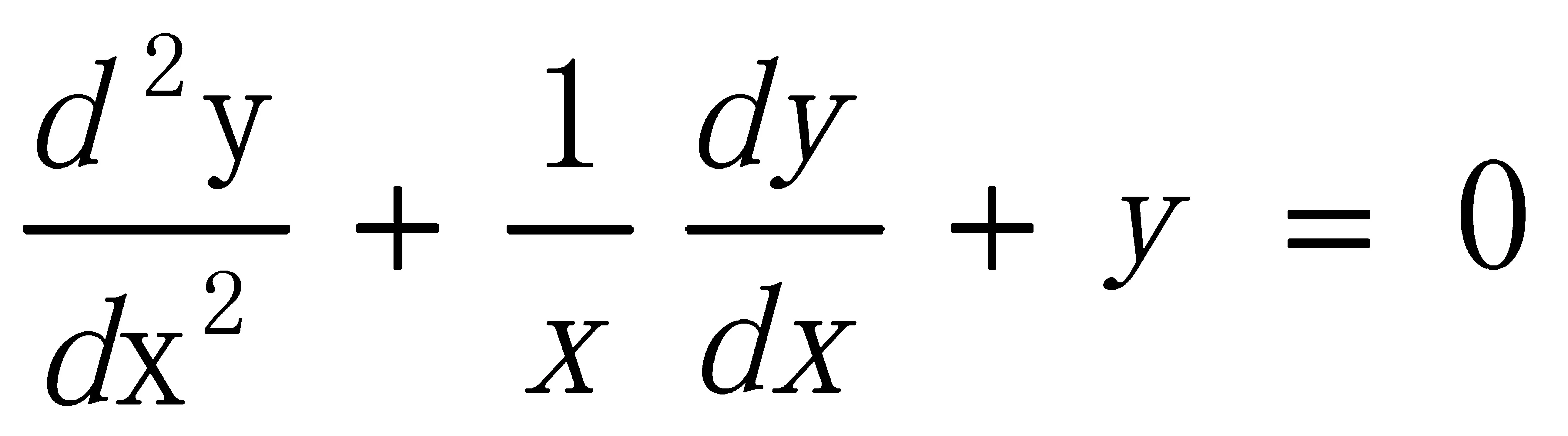
(1-14)

解得

(1-15)

令式中c=lnE，积分得

(1-16)

1.3 羽毛球拍面简正频率的理论解

(1-17)

根据膜振动理论可知，振型是根据不同的节圆数m和节径数n所决定的。拍面作自由振动时，必将存在无数的简正频率，其对应的简正振动方式为

(1-18)

其实部为

(1-19)

由上式可求得圆膜对称振动的节线位置，令

(1-20)

解得零阶贝塞尔函数的根值为

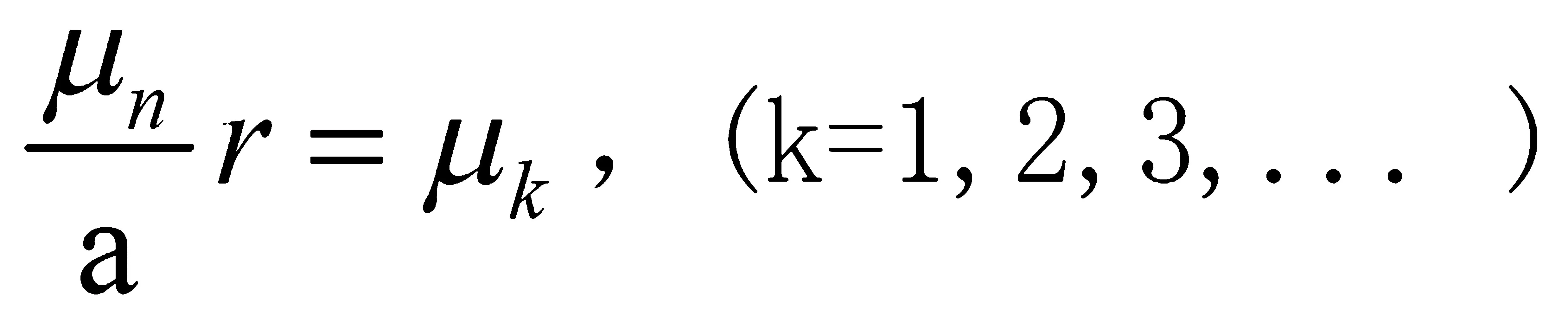
(1-21)

由此可得节线的位置为

(1-22)

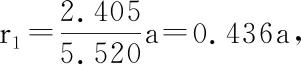
2. 有限元法及有限元分析软件

2.1 有限元法

有限元法是利用数学近似的方法对真实物理系统(几何和载荷工况)进行模拟，通过简单而又相互作用的元素(即单元)，就可以用有限数量的未知量去逼近无限未知量的真实系统。由于大多数实际问题难以得到准确解，而有限元法不仅计算精度高，而且能适应各种复杂形状，因而成为行之有效的工程分析手段。有限元法的求解过程如图2所示。

图2 有限元法求解过程

网面进行自由振动时，在理论上会发生无穷阶的阵型，但由于能量的衰减一般只考虑前几阶振型。网面在受力发生变形时，因为瞬时接触时间短，我们无法以肉眼看到网面自由振动的振型以及受力后网面变形量的大小。本文利用有限元法，通过有限元分析软件ANSYS中的WorkBench对网面进行模态和静力结构的仿真分析，将网面的振型和变形可视化。

2.2 有限元分析软件ANSYS简介

ANSYS软件是美国ANSYS公司研制的融结构、流体、电场、磁场、声场分析于一体的大型通用有限元分析(FEA)软件，其在机械、电机、土木、电子及航空等领域被广泛使用，是世界范围内增长最快的计算机辅助工程(CAE)软件。软件由前处理、分析计算和后处理三部分组成，具体流程如图3所示。通过使用该软件，不仅能够获得准确数据，而且还能缩短设计周期，降低预算成本[9]。

图3 ANSYS软件分析流程

ANSYS中的WorkBench是一种仿真平台模块，拥有各种与仿真分析相关的大型工程数据库、求解器、建模工具以及后处理器等组件程序，同时具备参数管理和设计优化功能，各项复杂的仿真任务都可以通过它实现。WorkBench中可以进行结构静态分析、模态分析、非线性分析、屈曲分析、谐响应分析、热分析、转子动力学分析等。本文主要对羽毛球拍网面进行模态分析和结构静态分析，并将计算结果与理论值进行对比。

2.3 羽毛球拍网面模态分析

模态分析是指用模态坐标去替换线性定常系统振动微分方程组中的物理坐标，经过方程组的解耦成为一组新的独立方程。也就是说，模态分析的本质是求矩阵的特征值，其“阶数”就是特征值的个数，将特征值从小到大排列就是阶次。实际的分析对象是无限维的，所以其模态具有无穷阶。但是对于运动起主导作用的只是前面的几阶模态，所以计算时只要根据需要计算前几阶即可。

模态分析是动力学分析最为基础的一种，模态分析用于确定机械零部件的振动特性及结构的自振频率特性，包括结构的固有频率和振型，它们是结构承受动态载荷设计中的重要参数。本文应用ANSYS的模态分析功能，对有预应力的网面振动进行模态分析。

任何结构系统都可以用下述动力平衡方程来描述

(2-1)

式2-1中[M]——质量矩阵

[C]——阻尼矩阵

[K]——刚度矩阵

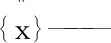
{x}——节点位移矢量

由于在对自由振动的系统求解固有频率和振型时，阻尼对整个系统的影响会比较迟缓即可以忽略不计，所以用ANSYS在进行计算分析时选择无阻尼模态分析。结构在没有阻尼作用下的动力平衡方程为

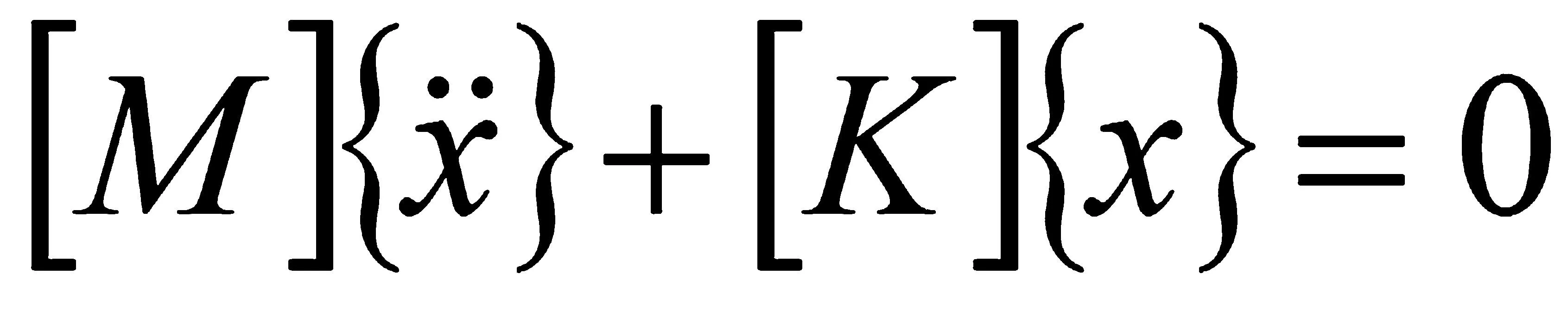
(2-2)

对于线性系统，上式解的形式为

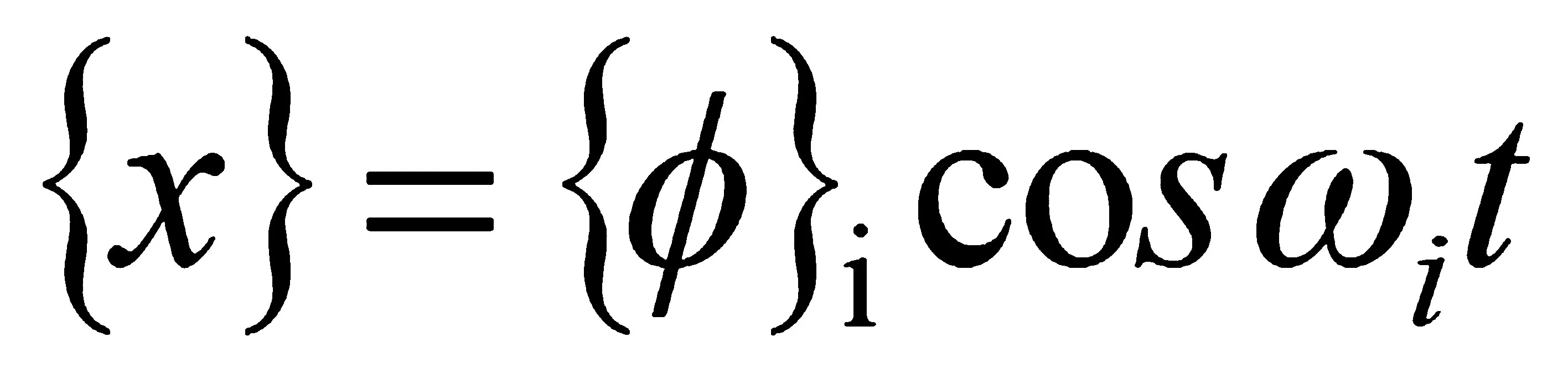
(2-3)

式中{Φ}i——第i阶模态对应的振型特征向量

ωi——第i阶模态的固有频率(单位为rad/s)

t——时间(单位为s)

将式2-3代入式2-2，得

(2-4)

由于当结构自由振动时，各节点振幅不可能都为零，因此就相当于求解系数行列式为零的解,即求其特征值。

2.3.1 前处理

2.3.1.1 创建分析项目

ANSYS WorkBench的工具箱中有多个分析项目，每个项目都分别显示着分析的流程，从中可以观察数据的流向以及分析的进度。多个项目的对象可以相互连接，并提供了一个可视化的表示。本文用了静力结构分析和模态分析两个项目，分别将两个项目的工程数据、几何模型、模型模块连接，以及将静力结构分析中的解决方案模块与模态分析中的设置模块相连接，项目概图如图4所示。

图4 创建分析项目

2.3.1.2 建立网面三维模型

由于在ANSYS WorkBench中可以直接导入SolidWorks的三维图，所以本文使用SolidWorks工程设计软件建模[10]。为了使ANSYS分析结果更加精确，确保模型的相似度是关键。根据国际羽联羽毛球比赛规则，要求羽毛球拍面长和宽分别不超过280mm和220mm。本文将拍面的外形近似为半个圆和半个椭圆组成。另外根据羽毛球拍网面穿线的特征，不难发现横纵两向中的所有相邻线的穿法是相反的，并且整个网面不在同一平面内，每一根线都是由多段直线和圆弧构成，因此网面的建模难度增加。本文通过手动测量得到每段直线距离和相邻两根线的距离，通过已知的线径、相邻两线距离和圆内弦的垂直平分线过圆心三个条件找到圆弧的圆心，从而得到圆弧半径，绘制圆弧草图如图5 所示，最后通过SolidWorks 三维建模中的扫描、阵列、拉伸、裁剪等特征功能完成网面的建模，三维图如图6所示。

图5 绘制圆弧草图

(a) 网面局部三维图

(b) 网面正视图

图6网面三维图

2.3.1.3 网面材料的设定

由于WorkBench 材料库中只有常规的材料，所以本文结合文献[11]中的数据，选用尤尼克斯BG65线加以计算，得到各参数值。通过手动方式添加羽毛球线的材料性能，即尤尼克斯BG65线的密度、杨氏模量和泊松比，具体参数见图7。

图7 尤尼克斯BG65线的性能参数

2.3.1.4 网面的网格划分

网格划分是整个模态分析过程中至关重要的一个环节，网格划分质量的好坏直接影响到后续计算分析结果的准确性。划分网格要进行总体模型规划，包括物理模型的构造、单元类型的选择、网格密度的确定等多方面内容(见图8)。本文中每根网线只受单一的拉伸力，精度要求不是很高，所以选择自动生成网格划分，全局网格控制如下图所示，网面网格划分示意图如图9所示。

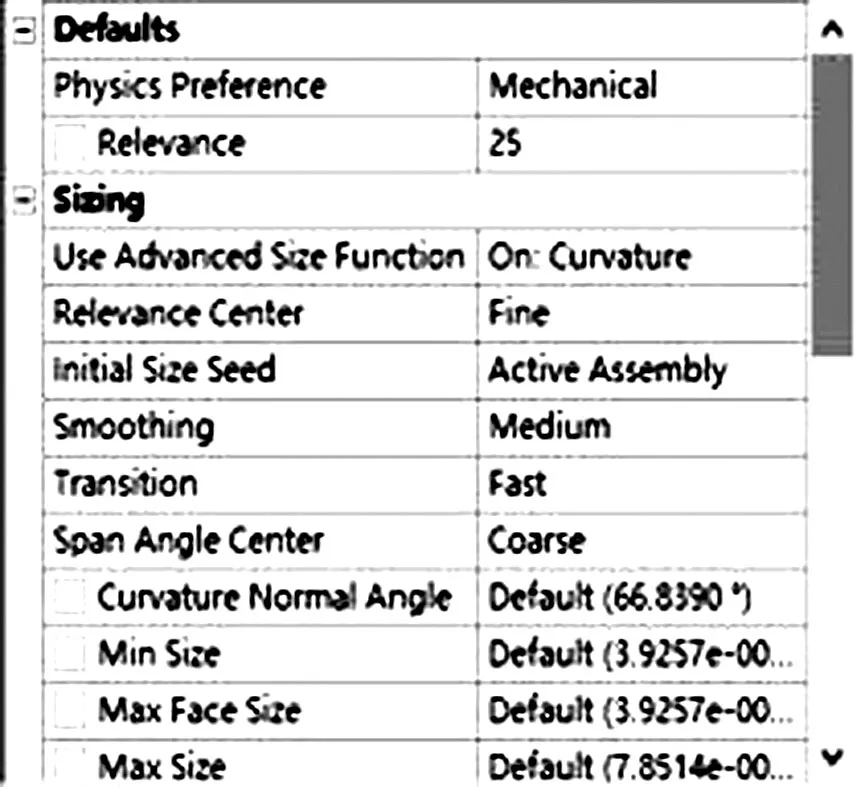
图9 网面网格划分

2.3.1.5 网面边界条件的设置

边界条件的加载也是至关重要的一个环节，其加载的正确与否直接影响到模拟结果。根据分析中边界条件是否随时间变化的情况，其加载的容易程度也就不同。一般而言，边界条件不随时间变化的加载相对容易，但要施加随时间变化的动态载荷就会比较困难。对于本文中的网面来说，网面周围一圈都要施加固定约束,并且每根线都受到向外的轴向预应力，这里按业余选手水平设定羽毛球拍穿线磅数为21磅即93.5牛顿。图10中，A代表固定、BCDE分别代表不同方向的预应力。

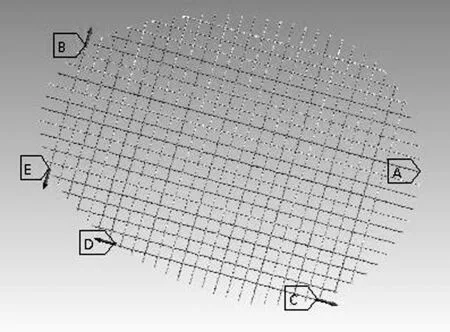
图10 施加边界条件

2.3.2 分析计算

在上述环境设定完成后，通过计算机直接求解可得网面各阶振型图，图11所示为部分阵型图。

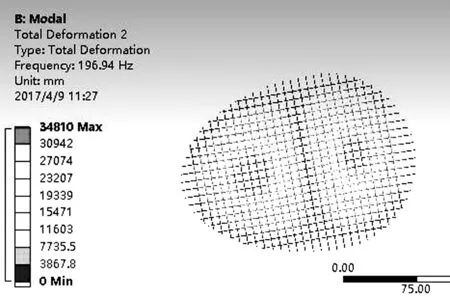
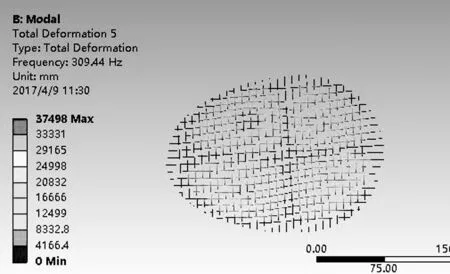
2.3.3 结果分析

为了验证将网面简化为圆膜假设的可行性，本文采用了理论和有限元计算两种方法，分别对周边固定、半径为95mm并承受21磅的圆膜和同样条件下的羽毛球拍网面，进行固有频率[12]与振型的求解。表1为其中两阶固有频率的理论解与仿真计算值两者对比。

表1 圆形薄膜与羽毛球拍网面固有频率及振型

由表1可以看出，拍面前二阶的理论解和仿真结果误差较小，两者得出的值虽然不完全相等，但都在同一个数量级。所以本文提出将羽毛球拍网面看作膜振动的设想是可行的，产生的误差有以下原因：

(1)理论计算是按照圆膜的外形计算的，与羽毛球拍网面的实际形状有差距；

(2)有限元计算时，网面建模不能和实际拍面完全一致。

2.4 网面结构静力分析

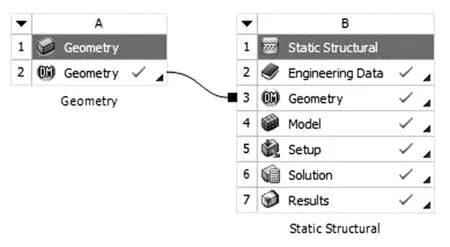
图12 创建项目分析

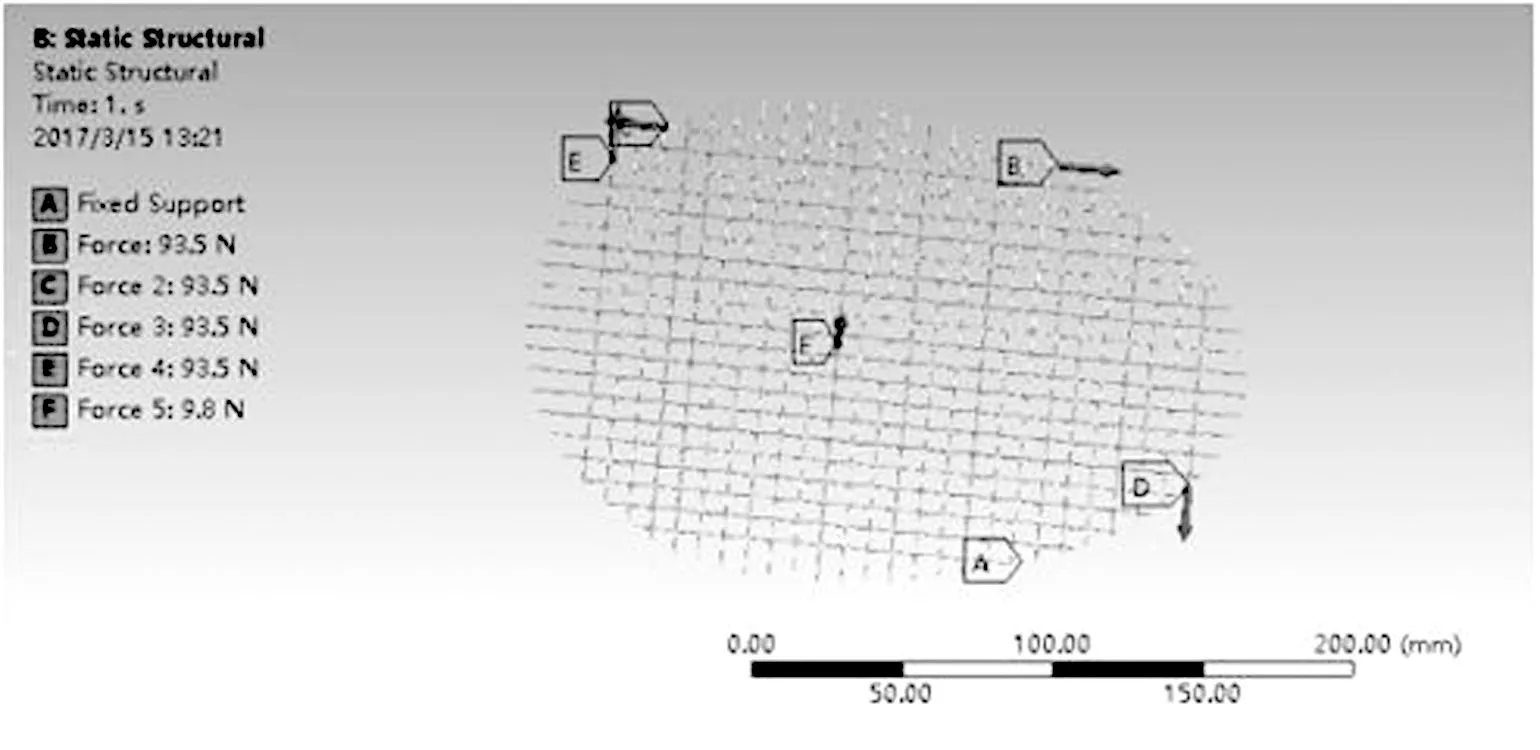
图13 边界条件施加

结构分析是有限元分析中最常用、最普遍的一个应用领域，它有七种结构分析类型。静力分析属于结构分析，它包括线性和非线性分析。与速度和加速度没有关系的对象主要用静力学分析来计算，它是研究静平衡关系的一种。

本文针对羽毛球拍网面进行线性结构静力分析(见图12)，其分析步骤同模态分析类似，区别在于要将模态分析项目去除；用羽毛球拍击球时，相当于网面在很短时间内受到一冲击载荷的作用，羽毛球重量约5克，击球时间按0.04秒计，击球速度取280公里/小时，经计算网面受力约为9.8牛顿，所以在约束边界条件时，在中点施加垂直于网面、大小为9.8N 的载荷，边界条件施加如图13所示；最后进行应力、应变和总变形求解，得到相应的云图(见图14)。

由分析结果可得，在中点施加P0=9.8N的力，其最大变形为ε=0.716mm。

3. 结语

本文运用膜振动理论和有限元分析软件，分别对羽毛球拍网面进行了理论计算和仿真分析，得到了部分固有频率和振型图。通过对比可知，将网面看成膜的设想是可行的，可以用膜振动理论对网面进行理论分析；本文还利用ANSYS软件对网面进行了静力结构分析，得到了应力云图、应变云图和总变形云图。以上工作为进一步对网拍类球拍网面的研究提供了理论依据和有效方法，并可为专业运动员和业余选手了解拍面性能，发挥球拍的最佳效果以提高运动效率提供理论依据。

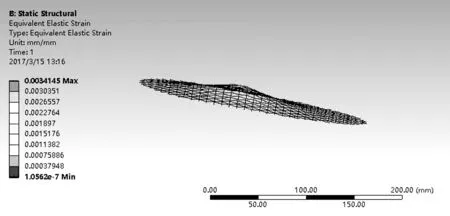
(a)应力云图

(b) 应变云图