Possible nodeless s±-wave superconductivity in twisted bilayer graphene∗
Zhe Liu(刘哲), Yu Li(李宇),2, and Yi-Feng Yang(杨义峰),2,3,4,†
1Beijing National Laboratory for Condensed Matter Physics and Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China
2University of Chinese Academy of Sciences,Beijing 100049,China
3Songshan Lake Materials Laboratory,Dongguan 523808,China
4Collaborative Innovation Center of Quantum Matter,Beijing 100190,China
Keywords: twisted bilayer graphene,superconductivity
The recent discovery of superconductivity in twisted bilayer graphene (TBLG) has attracted tremendous interest[1,2]in the condensed matter community. Depending on the twisted angle, TBLG can exhibit a large variety of exotic phenomena.[3-30]For a small twisted angle, as shown in Fig. 1(a), the lattice can form the so-called Moir´e superlattice[28-32]with strongly renormalized low-energy Dirac fermions.[20-28]At the so-called “magic angles”, their Fermi velocity can even be reduced to zero.[26-29]The superconducting phase in TBLG appears near the first magic angle (≈1.08°) on the hole-doping side (n <1), where the chemical potential is close to a van Hove singularity.The superconducting transition temperature is Tc≈1.7K with a renormalized electron bandwidth of about 10meV.[1]This was observed near a correlated insulating state at halffilling (n = 0.5). It is believed that the superconductivity might be mediated by the associated antiferromagnetic quantum critical fluctuations.[33-37]Many theoretical efforts[32-73]have been devoted to understanding the effective low-energy models,[37-48]the nature of the insulating state,[32,33,37-42,49-54]and the gap symmetry of the superconducting phases,[33,35-37,37,47,48,53-61]leading to the proposals of d+id-wave,[33-37,47,48,54-56]p+ip-wave,[47,52,57]nodal swave,[53,59]f-wave,[60]and even mixed gap symmetries.[58,61]The nature of the superconducting phases is a subject of heated debate.
The properties of the superconducting TBLG remind us of some of the features of heavy fermion superconductors like CeCu2Si2.[74,75]In CeCu2Si2, superconductivity is also mediated by magnetic quantum critical fluctuations, with Tc≈0.6 K and a heavy electron band of the width of a few meV,similar to those of TBLG. For decades, superconductivity in CeCu2Si2has been believed to be a d-wave,[75-77]but recent refined experiments have revealed two nodeless gaps.[78,79]It was pointed out that such a gap structure may be the result of the strong interband quantum critical pairing interaction between coexisting electron and hole Fermi surfaces in CeCu2Si2.[80]Since the low-energy effective model of TBLG may also have two bands,[37,38]we explore here the possibility of multiple superconducting gaps and study the detailed gap structures taking into account both intra-and interband pairing interactions. For this purpose, we adopt the strong-coupling Eliashberg approach and consider the magnetic quantum critical fluctuations as the candidate pairing glues.[80-89]In comparison with the experiment, we find the most plausible gap symmetry to be a nodeless s±-wave in the observed range of superconductivity. Moreover, when projected into the valley basis, we obtain f-wave pairing in the valley-singlet component and interesting topological features in the valley-triplet component. Our work highlights the multi-gap nature of the superconductivity in TBLG and the key importance of interband quantum critical pairing interaction. This suggests that TBLG might belong to the same class of unconventional superconductivity as iron-pnictide, electron-doped cuprate, and some heavy fermion superconductors.
Our low-energy effective model is constructed with one px-like and one py-like Wannier orbital on each site of the honeycomb Moir´e superlattice,[38,43]as schematically illustrated in Fig. 1(b). The resulting four-orbital model describes the four low-energy bands separated by two gaps of about 50meV from other bands.[16]At the first magic angle,the lattice constant is a ≈134 ˚A.The mini-Brillouin zone of the superlattice is greatly reduced,as shown in Fig.1(c). Following Refs.[38]and[43],we adopt the following effective model:

The first term gives the main feature of valley degenerate valence and conduction bands and can be expressed as

where i,j denote the sites, µ is the chemical potential which is responsible for doping away from the Fermi level, and ci=(cix,ciy)T. In this term, only the hoppings between the same pxor pyorbitals are considered and tijtakes the value of t1,t2,t3,t4depending on the distance between the i and j sites.We consider hoppings up to the fourth nearest neighbor. The second term lifts the degeneracy of the K and K′valleys and can be written as
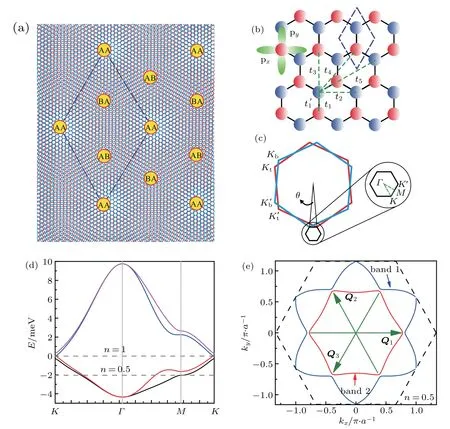
Fig.1. (a)Illustration of the Moir´e superlattice in TBLG with small twisted angle. (b)The honeycomb lattice for the tight-binding model used in this work. The px/y-like Wannier orbitals and the hopping parameters are labeled in the figure. In both(a)and(b),the regions enclosed by dashed lines represent a single super unit cell. (c)Illustration of the mini-Brillouin zone of TBLG.Kt and K′t (Kb and K′b)represent the two inequivalent valleys of the top(bottom)graphene layer. K and K′ represent the two inequivalent valleys of TBLG.Γ and M are the center and middle points of the K-K′line of the mini-Brillouin zone. (d)Effective low-energy band structures along the high symmetry lines in the mini-Brillouin zone. The dashed lines denote the Fermi energy for n=0.5(half-filling)and 1,where n is one fourth of the total occupation number. n <1 is at the hole-doping side. (e)Typical Fermi surfaces taken at n=0.5,where the two lower bands are half filled. Q1,Q2,and Q3 are the three nesting vectors used in our calculations.
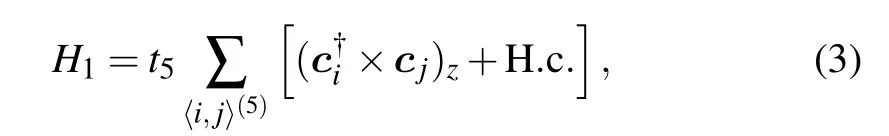
where the fifth neighbor hopping between the pxand pyorbitals is included. The last term including the nearest neighbor hopping t′1is
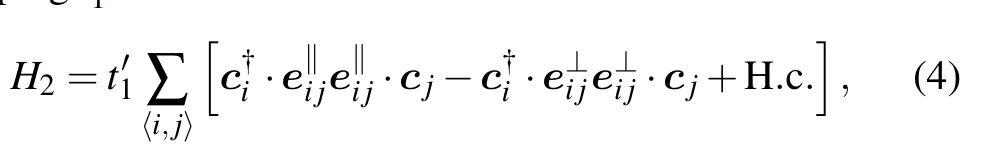
where e‖
ijand e⊥ijdenote the in-plane unit vectors in the directions parallel and perpendicular to the nearest-neighbor bond,respectively. This last term accounts for the hybridization between two valleys and generates a finite Dirac mass at K and K′points.[38]The parameters are chosen such that the bandwidth is of the order of 10meV and the doping level for halffilling of the two lower bands (n=0.5) is close to the van Hove singularity.Specifically,we adopt the values t1=2 meV,t2=0.3 meV,t3=0.05 meV,t4=0.15 meV,t5=0.12 meV,and t′1=0.1 meV. We have ignored the spin-orbit coupling(SOC) which is only ~1µeV in graphene and much smaller than the energy scale considered here.[90,91]Figure 1(d)plots the calculated band structures along high symmetry lines of the mini-Brillouin zone. The band structures at K suggest the coexistence of massless and massive Dirac fermions,consistent with both symmetry analysis[38]and quantum oscillation experiment.[1]The Fermi surfaces are nested near the van Hove singularity,as depicted in Fig.1(e)with the nesting wave vectors Q1=4π/3a(1,0), Q2=4π/3a(-1/2,3/2),and Q3= 4π/3a(-1/2,-3/2). A Lifshitz transition occurs when the chemical potential is tuned across the van Hove point.
To study the pairing symmetry of superconductivity, we apply the strong-coupling Eliashberg theory and consider two separated Fermi surfaces. The interband (finite momentum) pairing is ignored due to the absence of Fermi surface overlap.[80]Near Tc, the linearized Eliashberg equations can be written as
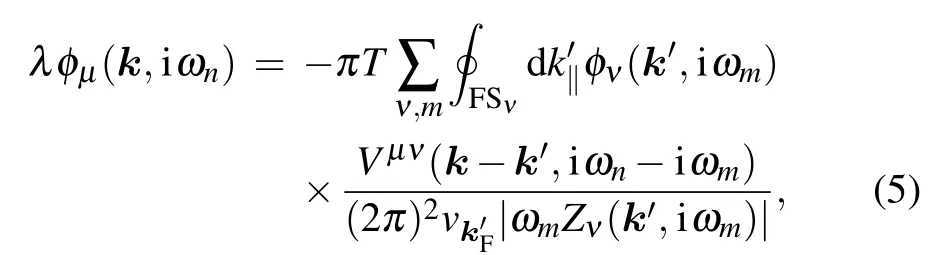
with
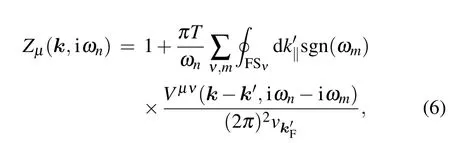
where µ and ν are the band indices, ωnis the fermionic Matsubara frequency,Zµ(k,iωn)is the renormalization function, and φµ(k,iωn) is related to the gap function through φµ(k,iωn)=Zµ(k,iωn)Δµ(k,iωn). Vµν(k-k′,iωn-iωm)represents the intra- or interband scattering of the Cooper pairs. This is an eigenvalue equation and each of its eigen solutions corresponds to a candidate pairing channel. The superconducting symmetry is determined by the leading channel with the largest eigenvalue λ at Tc. For quantum critical superconductivity,the pairing interactions take the phenomenological form[80,81]
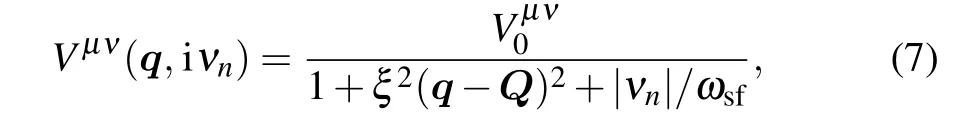
where ξ is the correlation length, Q is the antiferromagnetic wave vector, and ωsfis the characteristic energy of the quantum critical fluctuations. The values of ξ and ωsfare chosen such that the effective magnetic Fermi energy,Γsf= ωsf(ξ/a)2= 4.3meV, is approximately equal to the bandwidth of the two lower bands. Vµν0 are free parameters to be determined experimentally. The resulting gap structures only depend on the relative strengths r11=V110/V220and r12=V120/V220, while their absolute values play no essential role.
To solve the Eliashberg equations, we further approximate Δµ(k,iωn)=Δµ(k,iπTc)and Zµ(k,iωn)=Zµ(k,iπTc)and use 2048 Matsubara frequencies and 240×240 k-meshes in the mini-Brillouin zone. Typical solutions of the eigenvalue equations are plotted in Fig.2. The leading solution is a spinsinglet state with nodeless s±or doubly degenerate d-wave gap symmetry. This may be understood by recalling that the superlattice has a D3symmetry group with two one-dimensional and one two-dimensional irreducible representations. The s±-wave and degenerate d-wave solutions correspond to the A1:1,k2x+k2y,...and E:(kx, ky),(k2x-k2y, kxky)representations,respectively.A degenerate p-wave solution is also allowed in the E representation but never becomes dominant in the relevant parameter range. Figure 2(a)shows the four leading values of λ with varying r12at fixed r11=1.0. For small r12, the dwave solutions dominate,indicating that the intraband interaction favors d-wave superconductivity on both Fermi surfaces.Since dxyand dx2-y2are degenerate,the true gap function here is their linear combination,yielding a chiral d+id-wave pairing symmetry.[37,54]While for large r121.2,the leading solution is nodeless s±-wave, induced by a relatively strong interband interaction, as is in pnictide or some heavy fermion superconductors.[80,92,93]A nodal s-wave solution never wins out in the whole parameter range.Figure 2(b)plots the leading eigenvalues at fixed r12=1.1. With increasing r11, the dominant d and nodeless s±-wave solutions exhibit opposite tendencies,reflecting their different physical origins owing to the intra-and inter-band quantum critical pairing interactions,respectively. The momentum distributions of the two solutions are plotted in Figs. 2(c)-2(e). Although the dxyand dx2-y2components have nodes,the combined d+id solution is fully gapped. Therefore, both leading solutions are nodeless and may be hard to distinguish in the scanning tunneling experiment.

Fig.2. Evolution of the eigenvalues λ of four leading solutions with(a)r12 for fixed r11=1.0 and(b)r11 for fixed r12=1.1. (c)-(e)The gap distributions on the Fermi surfaces for a typical nodeless s±-wave solution and the degenerate dx2-y2 and dxy-wave solutions,respectively. We take as an example the results at n=0.5.
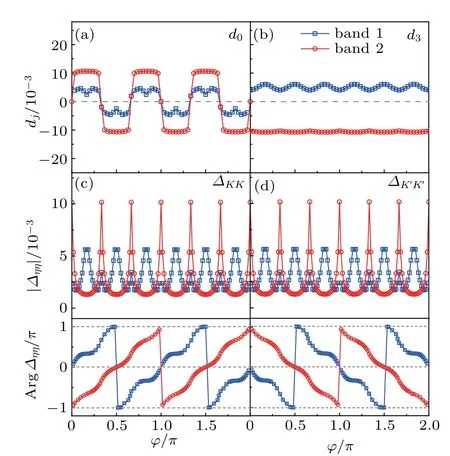
Fig. 3. Variation of the gap functions in the valley space with the azimuthal angle φ, showing (a) the valley-singlet component d0, (b) the valley-triplet component d3, (c) ΔKK = -d1+id2, and (d) ΔK′K′ =d1+id2 for a typical nodeless s±-wave solution of the band basis. The upper and lower panels of(c)and(d)plot the magnitude and argument of the two intravalley components,respectively.
While these solutions look simple, they contain certain topological features in the valley space. This may be analyzed considering Δηη′(k)=∑µaηµ(k)aη′µ(-k)Δµ(k),under a unitary transformation from band(µ)to valley(η)bases,cησ(k) = ∑µaηµ(k)cµσ(k), where aηµ(k) are coefficients of the transformation, cησ(k) and cµσ(k) are the electron annihilation operators in valley and band spaces. The resulting gap function can be quite generally decomposed into the valley-singlet and triplet components through Δηη′(k)=∑j[dj(k)τjiτ2]ηη′,where τjare the unit matrix for j=0 and the Pauli matrices for j=1,2,3. The magnitudes of d0and d=(d1,d2,d3)represent the relative importance of the valleysinglet and triplet contributions. Figure 3 plots the distribution of dj(k)on the Fermi surfaces for a typical solution of nodeless s±-wave as a function of the azimuthal angle φ. For spinsinglet pairing, the valley-singlet(triplet)requires odd(even)gap symmetry in the momentum space due to the Pauli principle. As shown in Fig. 3(a), d0indeed is an odd function in the momentum space. In particular,it has the same sign on both Fermi surfaces at the same azimuthal angle but the overall φ-dependence exhibits an f-wave manner. Thus the nodeless s±-wave solution in the band basis contains a valley-singlet fwave component. The angle dependence of the valley-triplet component is analyzed in Figs. 3(b)-3(d). Quite unexpectedly, while d3(k) is real and varies only slightly with momentum on both Fermi surfaces, d1(k) and d2(k) that correspond to intravalley pairing exhibit unusual topological characters. To see this, we introduce the gap functions on each valley individually, ΔKK=-d1+id2and ΔK′K′ =d1+id2,and plot the angle dependence of their amplitudes and phases in Figs. 3(c) and 3(d). A phase change of 4π or -4π is revealed as φ varies from 0 to 2π, which is a characteristic feature of topological superconductor with time reversal symmetry.[94]We thus conclude that the valley-triplet component has d±id-wave symmetry in the momentum space.We should note that the existence of ΔKKand ΔK′K′ is associated with the presumption of valley hybridization in our model Hamiltonian.[38]The relative importance of different valley components may be tuned by experimental manipulation of the valley degree of freedom.[95,96]Absent valley hybridization,the gap function becomes topologically trivial. A similar analysis may be applied to the d+id-wave solution in the band basis(not shown),where the d3and d1+id2components exhibit the phase change of-4π and-8π,respectively,implying its topological nature as chiral superconductivity.[94]
Our results are summarized in Fig.4(a)on a generic phase diagram with r11and r12as tuning parameters. There are two regions governed by the nodeless s±-wave for large r12and the d+id-wave for small r12. The overall phase boundary is only slightly shifted for different doping levels as shown in Fig. 4(b). Although an exact estimate of the relative importance of the intra- and inter-band quantum critical pairing interactions is not possible at this stage,some preliminary argument might still be made by considering∝(Q),where(Q)is the static spin susceptibility at the ordering wave vector Q and may be estimated under the first order approximation using the Lindhard function
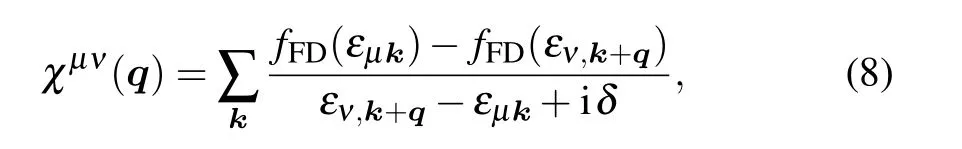
where fFDis the Fermi-Dirac distribution function and εµkis the dispersion of the µ-th band. Taking n = 0.5 once again as an example, we plot in Fig. 4(c) the real part of χ(q)=∑µνχµν(q)as a function of q. As expected,Reχ(q)reaches maximum when q approaches the nesting wave vectors (Q1, Q2, Q3) at the corners of the mini-Brillouin zone.The corresponding r11and r12can also be estimated and plotted in Fig. 4(d) for generic n. A direct comparison with the phase diagram in Fig. 4(b) gives the lower shaded area RC(0.4 n 0.6)in which the nodeless s±-wave solution dominates. Experimentally,superconductivity was observed in the upper shaded area labeled as RE. Their overlap implies that nodeless s±-wave is the most plausible gap symmetry for the superconducting TBLG near half-filling on the hole-doping side.
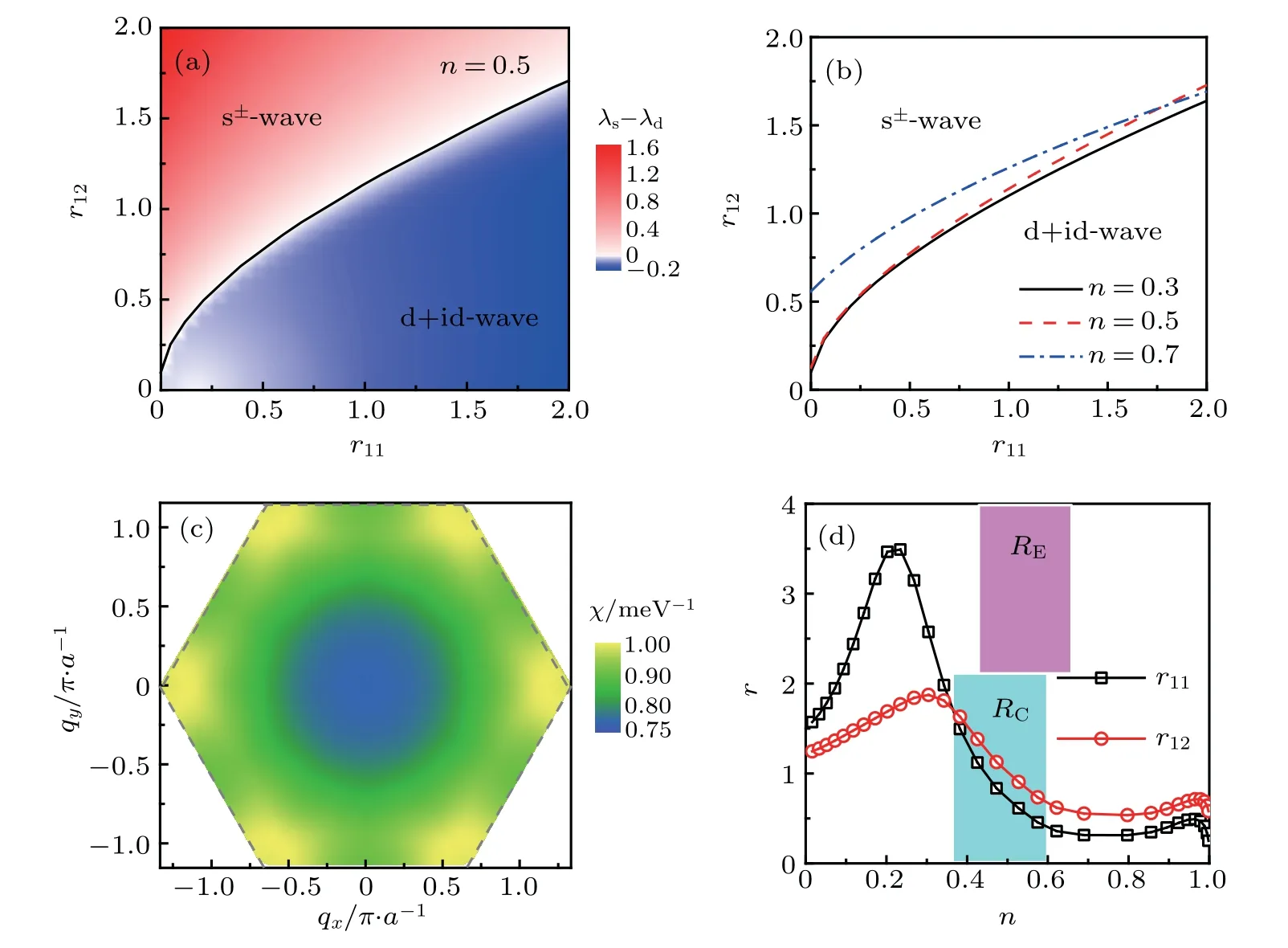
Fig. 4. (a) A typical theoretical phase diagram taken with n=0.5. The color is calibrated by the difference between the eigenvalues of the nodeless s± and d+id-wave solutions. The solid line marks the boundary of the two phases. (b)Variation of the phase boundary for different doping levels,showing only slight change with n. (c)The total spin susceptibility χ(q)evaluated from the Lindhard function,showing maxima at nesting wave vectors. (d) Variation of the estimated r11 and r12 as a function of the doping level. The shaded area RC denotes the range where the nodeless s±-wave becomes dominant,while the shaded area RE marks the region of superconductivity observed in experiment. The insulating phase(not indicated)is a very narrow region near half-filling within RE.
Our prediction of the nodeless s±-wave pairing symmetry is deduced from an effective low-energy four-band model with quantum critical pairing interactions and two coexisting Fermi surfaces due to valley hybridization. In previous studies,[33-37,47,48,54-56]a d+id-wave solution was often obtained without considering the presence of strong interband interaction. Absent valley hybridization,p+ip[47,52,57]or nodal s-wave solutions[53,59]have also been proposed depending on the topology of the Fermi surfaces. On the other hand, a more sophisticated analysis using the functional renormalization group (fRG) was shown to yield an f-wave solution.[60]Actually,this latter work might be consistent with the valleysinglet component in our nodeless s±-wave solution, as valley hybridization was neglected in the fRG calculations. Further experiments are needed to examine these various possibilities. However, we should note that both the nodeless s±and d+id-waves are nodeless in the momentum space. Therefore,it might be difficult to distinguish them with the usual scanning tunneling or photoemission spectroscopies. In this respect,phase sensitive measurements using Josephson devices for example[97]have recently been applied to the investigation of 2D topological superconductivity,[98]and Kerr rotation experiments may also be used to detect time reversal symmetry breaking in d+id or p+ip-pairings.[99]
To summarize,we explore possible gap symmetry of the superconductivity observed recently in TBLG based on a fourorbital model using the strong-coupling Eliashberg equations with a quantum critical form of the intra-and interband pairing interactions. We find a leading nodeless s±-wave solution for strong interband interaction and a dominant d+id-wave solution originating primarily from the intraband pairing interaction. Both exhibit interesting topological characters in the valley basis. A direct comparison between our theoretical and experimental parameter ranges suggests that the nodeless s±-wave is the most plausible candidate for the pairing symmetry in superconducting TBLG,different from previous theoretical proposals. The quantum critical nature of the pairing interaction has often been ignored in previous theories. Our work suggests a possible unified description for superconductivity in TBLG and some other correlated superconductors.
- Chinese Physics B的其它文章
- Coercivity mechanisms in nanostructured permanent magnets∗
- Progress in recycling of Nd-Fe-B sintered magnet wastes∗
- Grain boundary restructuring and La/Ce/Y application in Nd-Fe-B magnets∗
- Topology of triple-point metals∗
- Local evolutions of nodal points in two-dimensional systems with chiral symmetry∗
- Structural,elastic,and electronic properties of topological semimetal WC-type MX family by first-principles calculation∗

