Coercivity mechanisms in nanostructured permanent magnets∗
G P Zhao(赵国平), L Zhao(赵莉), L C Shen(沈来川), J Zou(邹静), and L Qiu(邱雷)
1College of Physics and Electronic Engineering&Institute of Solid State Physics,Sichuan Normal University,Chengdu 610066,China
2State Key Laboratory of Metastable Materials Science and Technology,Yanshan University,Qinhuangdao 066004,China
3Collaborative Innovation Center for Shanxi Advanced Permanent Materials and Technology,Linfen 041004,China
Keywords: coercivity mechanism,permanent nanomagnets,self-pinning
1. Introduction
Permanent magnets, which are available abundantly in modern life,[1-6]play an indispensable role as components of a wide variety of electromechanical and electronic devices.Roughly, an average home contains more than 100 permanent magnets and a car uses 12 on average. These magnets are being investigated,improved,and applied increasingly everyday, thus leading to a rapid change in our lives. In history, permanent magnetic materials marked the beginning of the magnetism.[3]The first use of the permanent magnets can be traced back to more than 2000 years ago in ancient China,where the prototype of the compass was invented and later used in navigation.
Permanent magnetic materials are characterized by their large coercivity and associated energy products, which could be millions times larger in comparison with soft magnetic materials. The application of the permanent magnets ranges from electric motors and generators,magnetic storage media,loudspeakers, door latches, and toys to ore separators, water filters,electric watches,and micro-tubes. These applications are related closely to the large coercivity, which can sustain for a long time. Therefore, coercivity mechanism is one of the key issues of permanent magnetic materials,and has not been completely understood yet. Generally, it is believed that the high coercivity is due to the high crystalline anisotropy K and hence the high anisotropy field Ha, as shown in Table 1. In comparison,the crystalline anisotropy of NiFe is of the order of 10 erg/cm3(1 erg=10-7J),representing one of the softest magnetic materials in nature.
In principle, the coercivity of the permanent magnet can be the same as its crystalline anisotropy field. However, the coercivity of most magnets is much smaller than the corresponding anisotropy field,leading to a paradox called as coercivity paradox.[17-19]Such a paradox was proposed by Brown in 1940s, which holds good for all kinds of permanent magnets, including the soft magnetic materials where the shape anisotropy field is dominant. The coercivity paradox is caused largely by the uncertainty of the coercivity mechanism in magnetic materials,especially in permanent magnets where the coercivity mechanism has been disputed for a long time.
Coherent rotation and curling are the main coercivity mechanisms of ideal materials,which are perfect in both phase composition and geometrical shape.[20-24]For these mechanisms to hold,the material must be an elliptical single-phased isolated grain without any defects, which can rarely be satisfied in real. Therefore, in general cases, nucleation and pinning are considered as the two dominant coercivity mechanisms, and the permanent magnets are classified accordingly into so-called nucleation-type and pinning-type materials.Nd-FeB is believed to be a nucleation-type material whereas SmCo a pinning-type material. However, some experimental results support the contrary conclusions.
Recently, it has been proposed that the real coercivity mechanism depends not only on the intrinsic magnetic properties of the material,but also on the microstructures such as defects and grain sizes.[10,25-27]Nucleation and pinning signify the beginning and end of the magnetic reversal respectively,and have to be analyzed as a whole. Therefore, the real coercivity mechanism could be a combined mechanism, which has the attributes of both traditional nucleation and pinning.Analyses show that interface pinning and grain boundary pinning are the dominant coercivity mechanisms of anisotropic and isotropic permanent nanomagnets, respectively. These two types of pinning are called as self-pinning, which occurs near the nucleation centers.
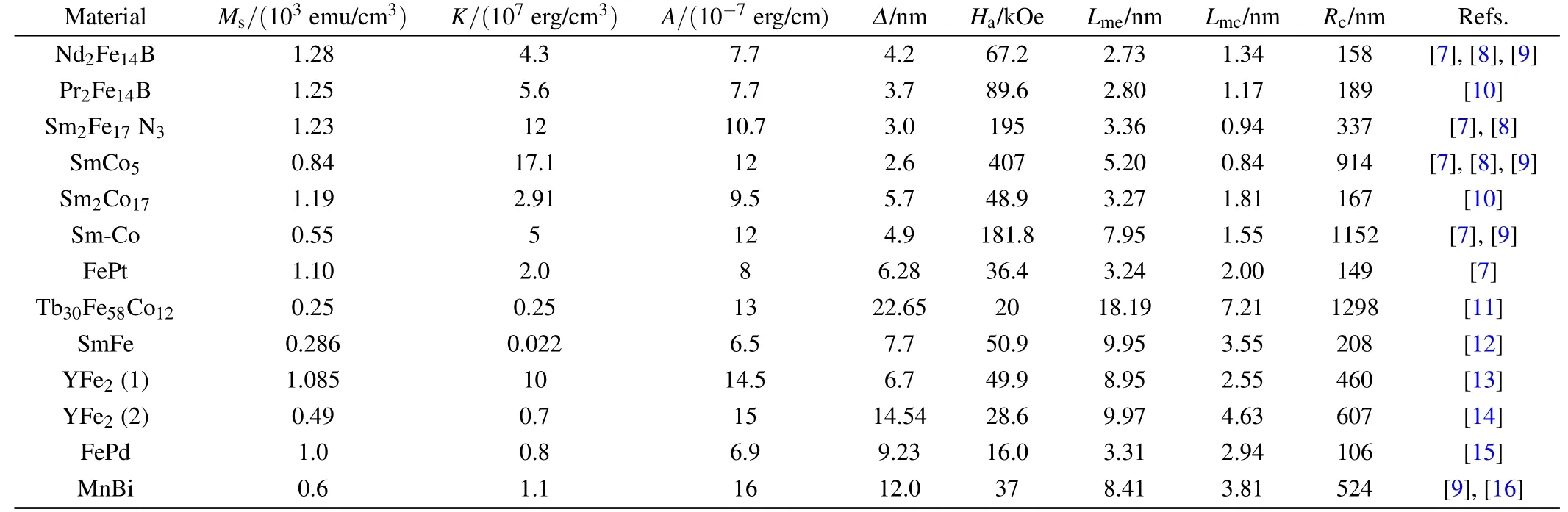
Table 1.Magnetic properties of various hard magnetic materials at room temperature,where Ms,K,and A denote spontaneous magnetization,anisotropy constant, and exchange constant, respectively Δ =π(A/K)1/2, Ha =2K/Ms, Lme =(A/2π)1/2/Ms, Lmc =(A/K)1/2, and Rc =9(AK)1/2/2M2s are Bloch wall width, anisotropy field, magnetostatic exchange length, magnetocrystalline exchange length, and estimated single-domain critical radius,respectively. The unit 1 Oe=79.5775 A·m-1.
The review is arranged as follows: In Section 2, various models of the coercivity mechanism are introduced and compared after a survey of the history of the permanent magnets and their main features. In Section 3, the recently proposed self-pinning mechanism for the nanostructured permanent magnetic materials are examined and compared with the other models. Such a pinning occurs at the interface between the main phase and the defects, which dominates the magnetic reversal process of well oriented permanent nanomagnets. Discussions are provided in Section 4 along with the main conclusions.
2. Hysteresis loops and a survey of various coercivity mechanisms
2.1. Hysteresis loops
Permanent magnets are characterized by a high resistance to demagnetization, i.e., a large coercivity. The coercivity of the permanent magnetic materials, typically the rare earth iron or rare earth cobalt magnetic materials, can be as high as 10 MA/m,[1-3,28]which is six orders of magnitude larger than that of the soft magnetic materials. In addition,a typical permanent magnetic material should have a large remanence to have a high maximum energy product(BH)max. This product describes the ability of a permanent magnet to withstand the influence of an external magnetic field. Moreover,the energy product is a measure of the useful magnetic flux that can be produced by the magnet in a given volume.[1-3]Figure 1 shows the magnetic flux density B plotted as a function of the magnetic field H,which is well known as hysteresis loop.The shaded area represents the (BH)maxproduct, the optimum working point that defines the largest area. The value of the(BH)maxis determined by the remanence Br,the coercivity

Fig.1. Hysteresis loop of a permanent magnet. The top shows the MH hysteresis loop and the bottom the B-H hysteresis loop. The shaded area represents the maximum energy product of the material.

Fig.2. History of the energy product achieved since 1880,the red dots denote the coercivity achievement.
In the history of the permanent magnetism, the relationship between the development of the magnetism and magnetic materials are reciprocal.[1-3,28]On the one hand, the advance in the magnetic materials progresses the theory of magnetism.On the other hand, the progress in magnetism accelerates the development of magnetic materials. As shown in Fig. 2, the(BH)maxvalues have increased by a factor of more than 100 in the past century.[1-3]Until the nineteenth century,magnets were weak,unstable,and made of carbon steel. Improvements were made with the development of cobalt magnet steels and alnico in Japan(Mishima)in 1917 and 1932,respectively.The coercivity of alnico was doubled when compared to other materials,owing to the shape anisotropy associated with a special metallurgical microstructure of an iron-rich Fe-Ni-Al-Co alloy. Further developments in the properties of magnets were achieved by the introduction of the rare-earth transition metal compounds in the 1960s,that are,SmCo5and Sm2Co17. Energy product with an excess of 200 kJ/m3was obtained,which is double of that of the best alnicos. However, these materials are expensive because of the Co component, which is expensive. In the 1980s, a novel type of permanent magnet material was obtained by combining Nd, Fe, and B, this defines the priority research area for high performance permanent magnets in recent years. Its importance lies not only onbHcand the squareness of the demagnetization curve in the second quadrant. HerebHcis used to represent the coercivity derived from the B-H loop to differentiate it from Hc,the intrinsic coercivity derived from the M-H loop. There are two kinds of hysteresis loops,one is the B-H loop and the other is the M-H loop. The two hysteresis loops are equivalent, with the magnetization M defined as M=B/µ0-H. While the B-H loop is used more often in the application area,the M-H loop is found to be used more conveniently in the research area. In the following,the hysteresis loops and their associated parameters such as remanence and coercivity refer to those of M-H loop.its substantially higher energy product, but also on its significantly lower raw material cost when compared to those of Sm-Co. Although remanence is important, the improvement in the(BH)maxis mainly due to the increase in coercivity.[1-3]The high coercivity of the permanent magnets is caused by their high anisotropy, either shape anisotropy or crystalline anisotropy. For the rare-earth permanent magnets, the crystalline anisotropy is responsible for the high coercivity.
2.2. Coherent rotation and domain wall motion
The mechanism of coercivity is an enduring topic of magnetism,[17,29-43]which is especially true because a permanent magnet characterized by a high coercivity is considered.The Stoner-Wohlfarth model(SW model)[44]is the most promising time-independent model to date. This model,based on the coherent rotation of the magnetic moments of singledomain grains with respect to their easy axes, gives the coercivity as Hc=Ha=2K/Msfor a bulk material with the easy axes parallel to the applied field direction. Here,K is the dominant crystal anisotropy constant,and Msis the saturation magnetization. The field Ha,thus defined,is called the crystalline anisotropy field,which is as high as 6.7 T for Nd2Fe14B.The corresponding remanence Mrgiven by the SW model is equal to Ms. For an isotropic material with random easy axes, the coercivity given by the SW model is 0.48Ha,roughly 3.3 T for Nd2Fe14B,and the remanence is 0.5Ms. However,it should be noted that in the later case, the magnetic reversal mechanism is not completely coherent. Rather, the moments in grains with different easy axes align in different directions, and the inter-grain exchange interaction is ignored completely. For a completely coherent rotation process,the coercivity is zero for a system with random easy axes as the average anisotropy is nullified. This explains why the coercivity values in noncrystallines are nearly zero,and can be extended to some nanocrystalline permanent magnets.
While the remanence determined by the SW model is in reasonable agreement with the experimental value, the coercivity of both experimental and technical magnets,however,is at most 20%-40%of that determined by the SW model. This discrepancy is generally attributed to the crystal defects and inter-grain interactions, which are ignored in the SW model.Despite these disadvantages,the SW model,proposed in 1948,is still widely used in magnetism. One reason is that it is a very simple analytical model,and can provide an appropriate coercivity mechanism. The other reason is that although the measured coercivity Hcis much smaller than that given by the SW model, the coercivity of all types of magnets are linked with the anisotropy field. In some models, this connection is expressed by introducing a term in the expression of the coercive field,which is proportional to Ha: Hc=αHa.[3,17,28-34]
In contrast to the rotation model, there is another group of models based on the motion of the domain wall,[3,17,28-31]proposed by Kersten and N´eel in 1940s. Here, the coercivity is owing to the hindering of the motion of the domain walls caused by the stress or impurities and is inversely proportional to cosβ, where β is the angle between the applied field and the easy axis. The coercivity determined by these models is generally much smaller than that determined by the coherent rotation of the magnetization. It has been agreed that the coercivity mechanism of multi-domain grains is mainly due to the wall motion while that of the single-domain grains is mainly due to the rotation. This, however, presents problems. For example,it has been argued[28,42-44]that although the domain walls exist in the magnets composed of multi-domain grains in the virgin state (thermally demagnetized state), when a large enough field is applied, no domain walls exist in the saturation state,which means that the grains are composed of single domains. Now if a demagnetizing field is applied,the domain wall has to be nucleated before it moves.Before the nucleation of the domain walls,it has to be ensured that the demagnetizing process of a material composed of multi-domain grains in the virgin state should be similar to that of the single-domain grains. Thus, the nucleation of the domain walls may be the dominant mechanism in some materials rather than the pinning mechanism. On the contrary, the domain wall motion and pinning are the main mechanisms of the initial magnetization curve, where the nucleation is not necessary. Therefore,the reversal mechanisms of the magnetization and demagnetization processes can be completely different. Nucleation was first considered by Brown and Frei et al. in 1940s and later by Aharoni et al.in 1960s,it occurs first at the crystal defects,surfaces,and then the corners of the material.
2.3. Various modes of nucleation and nucleation expansion
According to Brown,the field at which the original saturated state becomes unstable and some change in the magnetization configuration begins to occur is called as the nucleation field. Note that this definition differs from the implications of few later models, where the nucleation field means the field at which the dominant magnetic reversal occurs or at which a nucleus completes its expansion. This difference is one of the main reasons that are leading to the confusion of the coercivity mechanism in permanent magnets.
Based on the variational method, Brown arrived at a series of micromagnetic equations,and the nucleation field was determined by finding the eigenvalues of these equations. The coherent rotation, which was considered as a model for the hysteresis loops, turns out to be a nucleation mode with the nucleation field given by

where the first term originates from the crystalline anisotropy and the second term corresponds to the shape anisotropy.Ns=N⊥-N||, where N⊥and N‖are the demagnetizing factors perpendicular and parallel to the easy axis, respectively.For spherical grains, Ns=0 and equation (1) becomes equal to the crystalline anisotropy of the materials,which is the coercivity provided by the SW model for a bulk material with easy axes parallel to the applied field direction. In this sense,the SW model can be regarded as one mode of nucleation process,[28,38]namely,the uniform rotation.
“Curling”, “buckling”, or “twisting” are the other possible nucleation modes (non-uniform collective process).[17,28,29]Because of the non-uniform magnetization,these configurations will give rise to an addition of exchange energy. A barrier characteristic of each of these configurations should replace the barrier associated with the uniform rotation. The effective process will be the one where the absolute value of the nucleation field is the smallest. This depends on the diameter of the elongated grains concerned.In some cases,one of these non-uniform processes may be more economical than the uniform rotation, but the coercive force is less than that of the uniform rotation.
Frei et al.[45]and Aharoni et al.[46,47]compared the coherent rotation and non-uniform processes in the case of a prolate ellipsoid. For nonuniform processes,the critical field depends on the dimensions of the ellipsoid.[22]For example,the critical field of a sphere for the curling mode is as follows:[28]

where A is the exchange constant,R is the radius of the sphere,and q2=2.0816 is a dimensionless constant.
Comparing with Eq. (1), and taking into account that Ns=N⊥-N||=0 for a sphere, it is evident that if there is no other mode, the magnetization reversal in a sphere should start by the coherent rotation if R <Rc, and by the curling if R >Rc,where:

is the critical radius. This formula provides the small critical radius of the rare-earth permanent magnet, which is roughly 9 nm,for Nd2Fe14B sphere. When R is deviated from Rc,the difference between the nucleation fields of a soft grain for different modes could be quite larger. For an Fe grain with the minor radius of the order of Rc, Hcritis typically 0.1 times of the critical field obtained for uniform rotation. For permanent magnets, however, the first term in Eq. (2) is dominant.Therefore, the critical field difference is rather small. For an Nd2Fe14B grain with the minor radius of the order of 10Rc,the second term in Eq.(2)can be ignored,and Hcritis 0.76 times of the critical field obtained for uniform rotation.
For the other grain shapes, other processes may be involved in the magnetization reversal,[23,30]but in every case,the uniform rotation tends to occur for small grains,and nonuniform processes tend to occur for larger grains. However,the difference in the coercivity of different modes in hard magnets is rather small. Besides,the consideration of the nonuniform processes cannot solve the coercivity paradox in the hard magnets completely.
Besides the nucleation model, there is another type of model for the formation of the early domain walls in the demagnetizing process called as the nucleus expansion model,[29]proposed by Givord et al.in 1980s. Although both models,with the adequate selected parameters,have been applied successfully, their respective philosophies are different.The nucleation model,as a micromagnetic approach,can shed light on the reversal mechanisms, whereas the nucleus expansion model, as a global approach, cannot. By contrast,thermal activation effects are intrinsically considered in the“global”model,whereas they are neglected in the micromagnetic approach.[29]
In permanent magnets, the origin of the coercivity has been debated intensely for decades.[3,30-34,44-53]Both nucleation and pinning models have some experimental support,but they have failed to explain few experimental phenomena.Therefore,a conclusion has been made that there are two types of permanent magnets according to the different coercivity mechanisms, nucleation type and pinning type.[1-3,17,28-34]It is believed that the coercivity mechanism of Sm2Co17material is mainly pinning dominant, while that of sintered Nd-Fe-B material is nucleation dominant. Consequently,the differentiation of the coercivity mechanism of the permanent magnets in the 20th century is phenomenological.
2.4. Numerical approaches and more advanced models
The turn of the century offers the possibility of investigating the coercivity mechanism in the permanent magnets based on the full micromagnetics. On the one hand, with the increase in the calculation power of the computers, numerical approaches to the magnetization reversal are developing rapidly. On the other hand,recent experimental techniques aid the fabrication of the nanostructured permanent magnets with reliable measurement of microstructures and grain sizes. The theory and experiments can be compared to reveal the underlying coercivity mechanisms.
Micromagnetics, as a bridge between the quantum magnetism and macroscopic magnetic phenomena, can yield the demagnetization process of permanent magnetic materials directly,in addition to the domains and domain wall structures.These calculations are initiated from the total magnetic Gibbs free energy, ΦG.[47,54-58]The calculated magnetization is a continuous function of the magnetization, which has a constant magnitude, but a variable direction. However, full micromagnetics in the permanent magnets(including composite magnets) suffers from a large compute power needed due to their very thin domain wall,typically 3 nm-5 nm,and thus requires a mesh size less than 1 nm to mimic the domain wall correctly. The main task of the numerical approaches is to evaluate the dipolar fields,where various numerical techniques are used. The finite difference method provides an easier approach,but it is limited to the simple description of the physical system. The finite element techniques are difficult to handle,but they can describe complex shapes.
In addition,the other problem is the minimization of the energy ΦG. To overcome this problem,the conjugate gradient method is often used. However, it is not suitable to describe unsymmetrical processes,which occur in the symmetrical systems during magnetization reversal.Therefore,a damping factor from the Gilbert-Landau equation[28,29,59,60]is used.
Moreover, all the above models have common disadvantages when compared to the SW model,i.e.,the calculation of the hysteresis loop is complicated, and in most cases, the coercivity cannot be derived simply by the analytical methods.There is a large gap between the simple SW model and the detailed models.The SW model,although very simple,is widely used as a common reference. Considering this,it is necessary to make a compromise between the simplicity and accuracy.
Therefore,various micromagnetic theories have been proposed, with quite a few models based on the magnetization reversal process.[33,44]Nucleation and pinning are believed to be the two important coercivity mechanisms in both singlephased and exchange-coupled composite permanent magnets.A self-pinning coercivity mechanism has been proposed recently, incorporating elements of both initial local nucleation process and subsequent propagation of the domain wall to the main phase.[10,25-27,61-63]Such a mechanism was first proposed in hard-soft multilayers, which was then extended to composite and permanent nanomagnets.The defects in the socalled single-phased permanent magnets act as the nucleation and pinning centers, which play a role similar to that of the soft phase in hard-soft composite systems. Such an interface pinning dominates the magnetic reversal process of well oriented permanent magnets,as found in either one-dimensional(1D)[7,64-66]or three-dimensional (3D)[67-69]micromagnetic calculation.
Further, a new analytical model was recently proposed to investigate the important role played by the transition region in the reversal process of isotropic permanent magnetic materials,which is a special domain wall formed in the grain boundary.[18,19]The model provides a simple and easy way to calculate the hysteresis loop and gives simple formulae for the remanence and coercivity. It is worth noting that this simplicity is retained by ignoring the magnetostatic interactions,which play a relatively less important role in the demagnetization process of isotropic permanent magnets compared to the crystalline anisotropy and exchange interaction.
Nevertheless, such a model is much more accurate than the SW model because the exchange interaction is explicitly included in the model to investigate the underlying coercivity mechanism in the permanent magnets. The coercivity mechanism in this case turns out to be another special kind of pinning, which is pinning in the grain boundary with different easy axes.
3. Interface-pinning of well-oriented permanent magnetic systems
This section discusses the role of crystalline defects,which play a significant role in the demagnetization process and in reducing the coercivity considerably. Generally these defects possess two competing effects, nucleation of the reversed domains and pinning of the domain walls. In the nucleation models, as nucleation centers, they are responsible for the low measured coercivity. However, in the pinning models, they can retain the coercivity by supplying pinning centers. Both models have their experimental supports. However, it is exceptional that a sole experiment can support both mechanisms sometimes.[2,28]A self-pinning mechanism has been proposed recently, which can explain this contradiction.[10,25,61-63]The defects can lower the local anisotropy and are responsible for the reduction of the nucleation field,which is responsible for the formation of the local reverse domains. These domains are pinned at the nucleation centers because of the large difference between the magnetic parameters of the defect and the main phase until the applied field is larger than the pinning field.When H >HP,the reverse domain can move into the main phase and hence sweep the whole material,settling the magnetic reversal process. Hence,where there is a nucleation center, there exists an associated pinning field. The self-pinning coercivity mechanism is thus defined,and is found to be the dominant mechanism in permanent and composite nanomagnets.
Such a self-pinning coercivity mechanism is based mainly on the micromagnetic analyses.In this section,reliable nucleation and pinning fields,as well as the coercivity mechanisms,have been obtained for a planar soft defect with a thickness 2d sandwiched inside a hard bulk system with uniaxial easy axes. This calculation is similar to an exchange-coupled triple-layer magnetic system. The results are then extended to general nanocrystalline permanent/composite magnets and are compared with the experimental data. Finally,the influence of the microstructures on the coercivity and its mechanism is discussed.
3.1. Basic formulation
In this section, a step-like anisotropic defect is considered, forming a hard/soft/hard trilayer system. Here, both spontaneous magnetization and exchange constant change abruptly at the interface in addition to the crystalline anisotropy. The crystalline easy axes of the main phase are parallel and that of the defect are perpendicular to the direction of the applied field. Both of these are within the layer plane so that the magnetostatic interaction can be ignored.
Similar to a hard/soft multilayer,[26]the total magnetic energy per unit area for such a defect sandwiched in the permanent magnet can be expressed as follows:

where θ is the angle between the magnetization and the applied field H. Owing to the symmetry, only half of the trilayer system is considered. The superscripts p and d denote the main phase of the permanent magnet and the soft defect,respectively.
The variation in the total energy density leads to two independent equations. The variation of the volume part results in the Euler-Lagrange equation:

By solving Eqs.(5)and(6)with suitable boundary conditions,we obtain the angular distribution in the soft defect and the main phase as two elliptical integrals.
Further,the interface constraint[26,27]can be rewritten as follows:
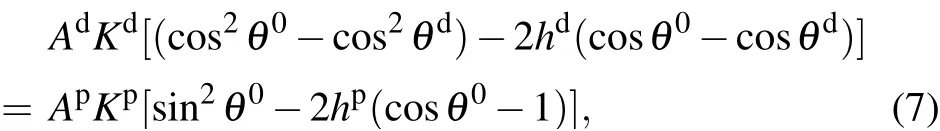
where θ0is the direction of the magnetization at the interface,z =0. The reduced applied field, h =H/Hais introduced,with Ha=2K/Msas the anisotropy field. Δ =π(A/K)1/2is the Bloch wall width. Equations(5)-(7)form the basis of the calculation.
3.2. Comparison of nucleation and self-pinning fields
At the nucleation state, the deviation of the magnetization from the applied field direction is small, and therefore the nucleation field can be derived analytically by series expansion.[22,31]A Taylor series expansion of Eqs.(5)and(7)at θ =0, without the high-order term and after a subsequent integration,yields the following:
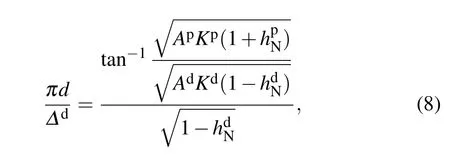
where hN=-HN/Hais the reduced nucleation field. A minus symbol is adopted here,as we are investigating the nucleation corresponding to the second quadrant hysteresis loop.
Equation (8) is a general formula that relates the nucleation field to the defect thickness 2d and material parameters.From this relationship,more formulae can be derived. For example,by substituting Kdwith-Kdin Eq.(8),we arrive at the nucleation field for a soft defect sandwiched in the permanent magnet with parallel easy axes,

Similar equation has been derived by Zhao et al.[27]for a hard/soft multilayer (Eq. (5) of Ref. [47]). If we ignore the effect of the anisotropy in the soft defect Kd,equations(8)and(9)become equivalent,and can be simplified as,

Similar simplification has been adopted by many literatures,[21,22,24]for the hard/soft multilayers. However, it is not always correct. Further simplification of Eq. (10) by considering=,=yields πd/=cos-, which is the formula of the nucleation field for a step-like anisotropy derived by Aharoni.[46]

Fig. 3. Calculated nucleation fields for a planar α-Fe-like soft defect sandwiched in Nd2Fe14B with perpendicular and parallel easy axes,which vary with the soft defect thickness d. In addition,the nucleation field for Kd =0 is shown for comparison, i.e., when the anisotropy in the soft defect is ignored completely.

Table 2. Magnetic properties of various soft defects at room temperature. NA means that the data are not available.
Figure 3 shows the 2d-dependent nucleation field calculated according to Eqs. (8)-(10) for Nd2Fe14B with α-Fe as the soft defect. The material parameters are listed in Table 2.All the three HNdecrease uniformly as d increases, and saturate at sufficiently large d. For small d, Kdhas negligible effect on the nucleation field, and therefore, the three curves converge into one single curve. However, for large d, there are clear gaps between the three curves and Kdcannot be ignored. The nucleation fields according to Eqs. (8)-(10) saturate at-540 Oe,540 Oe,and 0 respectively.
It is noted that the negative nucleation field has been obtained for the trilayer system with perpendicular easy axes.This finding is consistent with the experiment results,where it was found that the domain walls could be nucleated before the remanent state has reached.[2]However,the calculated nucleation field is much smaller than the experimental coercivity for larger 2d, suggesting that the nucleation is not the dominant coercivity mechanism in these materials. In fact, the nucleation is necessary, but not a sufficient condition for complete magnetic reversal. In addition,it sets a lower limit to the coercivity.
Figure 4 compares the calculated nucleation field with the coercivity with easy axes perpendicular and parallel to the defect plane, where a planar α-Fe like defect with thickness d is sandwiched in Nd2Fe14B.It is evident that the coercivity is identical to the corresponding nucleation field only for 2d less than a certain critical size,Lcrit1,where the dominant coercivity mechanism is nucleation. For Nd2Fe14B/α-Fe/Nd2Fe14B trilayer system,Lcrit1=4 nm. For large 2d,there is a gap between the two fields and the coercivity is identical to the pinning rather than the nucleation field. Therefore, in this case,pinning is the dominant coercivity mechanism. Experimental results[71]of hard/soft/hard multilayers show a similar trend in the change of the coercivity mechanism,as shown in Fig.5.For sufficiently large d, Hcsaturates at approximately 7 kOe,the smallest pinning field,which can be derived analytically:
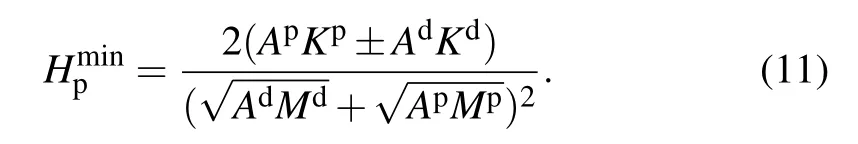
Here, a “+” is adopted for perpendicular easy axes, while a“-” is adopted for parallel easy axes. Generally, the pinning field decreases with the soft layer thickness.

Fig.4. Comparison of nucleation and pinning fields for a planar α-Fe like soft defect sandwiched in Nd2Fe14B with easy axes perpendicular and parallel to the defect plane.
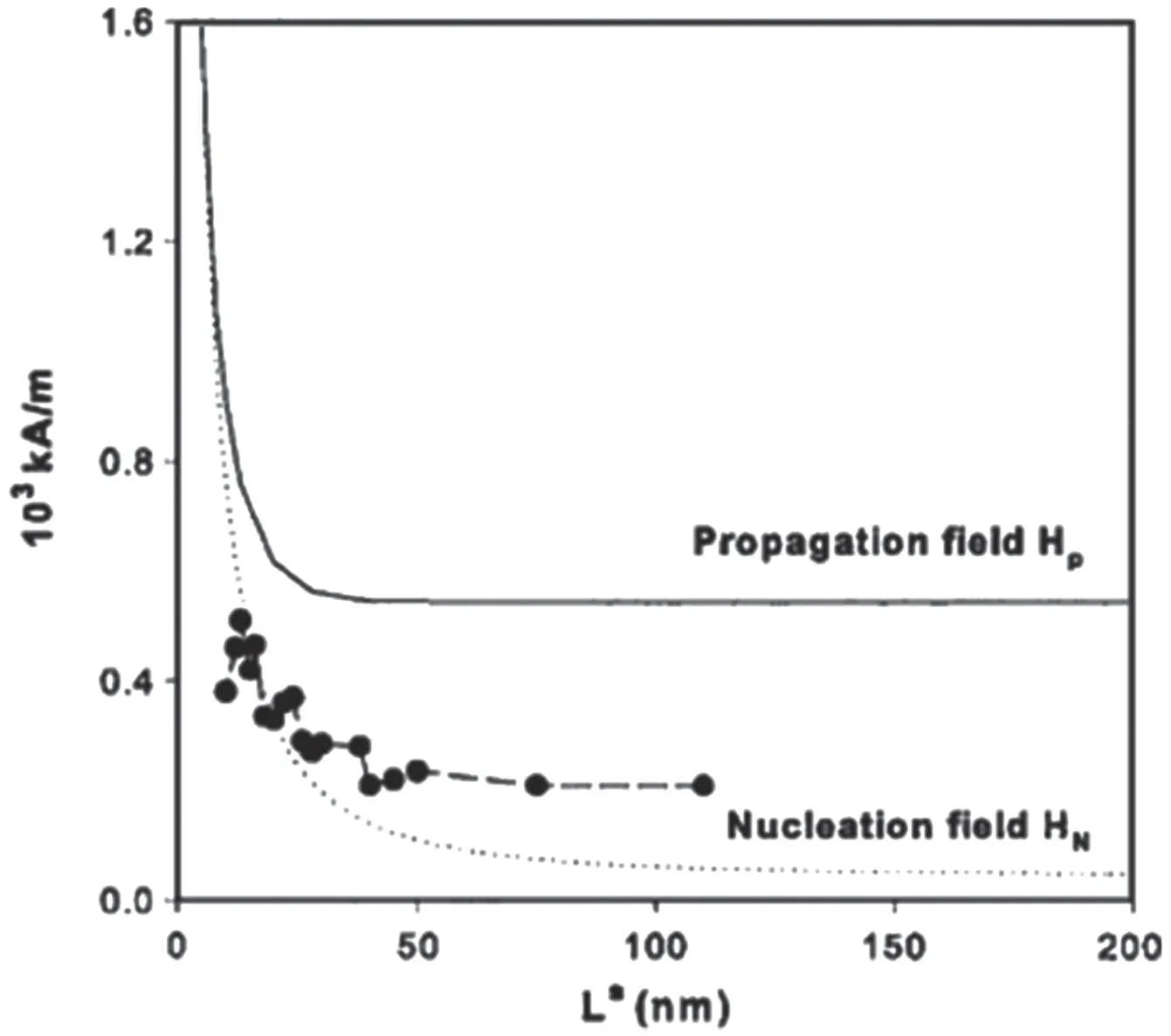
Fig.5. Comparison of the calculated nucleation(dashed)and propagation fields(solid)for NdFeB/Fe multilayers with the experimental data.The solid circles denote the experimental coercivity obtained for the NdFeB/Fe/NdFeB trilayer system.[26]
Such a pinning has the attributes of both traditional nucleation and pinning. On the one hand, by considering a“-”in Eq.(11),the numerator r of the right-hand side of Eq.(11)represents the domain wall energy difference of the hard and soft phases. Thus,the field given by Eq.(11)is because of the fact that the domain wall in the hard phase has much higher energy density than that in the soft phase. This implication is similar to that of a typical pinning field. In fact, similar equations to that of Eq.(11)have been obtained by other groups,[33]which is called as the pinning field.In addition,as illustrated by Zhao et al.,[26]from Eq.(11),other formulae for pinning fields can be derived.
On the other hand, the pinning field given by Eq.(11)is in fact a propagation field,at which a local domain wall could fully grow and break away from the local nucleation site,and then propagate into the main phase. From this point of view,the self-pinning field can be regarded as a kind of nucleation field. If we ignore the Kd,equation(11)can be rewritten as:

Kronm¨uller et al. obtained a similar formula as Eq.(12)for NdFeB and PrFeB materials,and they considered it as the nucleation field.[72-74]This pinning is inherently linked with the nucleation centers and is called as the self-pinning by Zhao et al.Once the domain walls enter the hard phases,they have to overcome the other pinning centers to spread throughout the whole material.The pinning field provided by these traditional pinning centers is generally smaller than the self-pinning field of the permanent and composite magnets.Thus,the traditional pinning can be ignored in the following discussions.

Fig.6. Comparison of the calculated nucleation fields for two different spherical soft defects in the NdFeB matrix.
The self-pinning field provided by Eq. (11) or Eq. (12)is completely determined by the interface constraint,which is independent of the interface shape. While the pinning field provided by Eq. (11) can be applied to other magnetic structures,the nucleation field cannot be applied,as it differs with the geometries. For a hard matrix with spherical soft inclusions,HNcan be derived as follows:

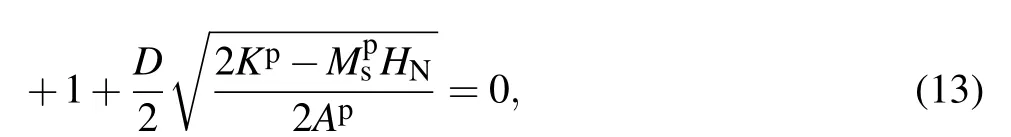
where D is the diameter of the soft inclusion. Similar to those shown in Fig.4 and discussed above,the nucleation field shown in Fig.6 is generally smaller than the self-pinning field given by Eq.(11),particularly for a large defect size/thickness.For an exchange-coupled material consisting of many nucleation centers,the coercivity is determined by the smallest selfpinning field,which corresponds to the largest defect size. In this region of the defect size,as shown in Fig.4,the coercivity mechanism is pinning rather than the nucleation. Therefore,the dominant coercivity mechanism in nanostructured permanent magnets is self-pinning,and the coercivity is determined by the smallest self-pinning field of the material, which in many cases,is approximately given by Eq.(12).
3.3. Experimental evidence and comparison with other theories
Kronm¨uller et al. have made an extensive effort in revealing the coercivity mechanisms in the permanent magnets,both theoretically and experimentally.[72-75]By careful fitting of temperature dependence of the coercivity over a wide temperature interval, they found that the experimental coercivity is a linear function of Ha, i.e., H =αHa+NeffMs, for various permanent and composite materials. Apart from a correction term due to the shape effect,this equation is the same as Eq.(12). For the exchanged-coupled permanent/composite magnetic systems discussed here, the correction term is very small and can be ignored. The fitted α for those materials are listed in Table 3.[72,75]

Table 3. Fitted α for various materials by Kronm¨uller et al.,where NA means that the data are not available.
It is of interest that they conclude that the dominant mechanism in NdFeB and PrFeB materials is nucleation while that in SmCo is pinning based on these results.[72-75]They argued that, in the case where the domain wall pinning would dominate the demagnetization process, an increase in the coercivity has to be expected. The large difference between the magnetocrystalline energy of Nd2Fe14B/Pr2Fe14B and α-Fe would result in strong pinning centers, as the domain wall energies for the two phases are quite different.[72,75]Therefore, the pinning mechanism cannot be considered as the dominating mechanism in Nd2Fe14B/α-Fe and Pr2Fe14B/α-Fe systems.[72,75]To clarify this,we may rewrite Eq.(11)as:

It is evident that the existence of α lowers the pinning field considerably and the self-pinning cannot be excluded from the coercivity mechanism in these systems. In fact, these data can be explained well by the self-pinning mechanism.From Table 3, it is evident that all the fitted values of α for Nd2Fe14B/α-Fe system are approximately 0.1, which is consistent with the calculation based on the self-pinning mechanism. As the volume occupied by the soft-phase increases,the largest soft grain size in the material increases, which leads to the decrease in the coercivity. The parameters (Ms, Ha) of Pr2Fe14B is similar to that of Nd2Fe14B,thus Pr2Fe14B/α-Fe has almost the same coercivity as that of Nd2Fe14B/α-Fe. As for the SmCo system,different annealing temperatures lead to different grain sizes,which in turn result in the different largest“soft”grain sizes. The most likely“soft”grains in the SmCo system is Co.The fitted values of α for this system are roughly 0.4, much larger than that derived from Eq. (14), which is approximately 0.2 for both the Sm2Co17/Co and SmCo5/Co systems. This suggests that the materials are probably nearly stoichiometric with very small inclusion of Co.
In short,the main coercivity mechanism in the exchangecoupled permanent magnets is interface-pinning, which has the attributes of both traditional nucleation and pinning. This nucleation-pinning duality helps in solving the long-lasting disputes on the coercivity mechanism in permanent/composite magnets, and it explains the available experimental data quite well. This coercivity mechanism, proposed in the hard/soft/hard trilayers,can be extended to almost all the composite and permanent nanomagnets as a dominant mechanism.Particularly, such a mechanism can be extended to sintered magnets where the grain size is much larger than 1 µm and the defect size is nearly 1µm or slightly smaller. One can see that,in this case,d can be considered large enough so that the pinning field is the lowest, which is approximately 0.1Hafor Nd2Fe14B with Fe as a soft defect.
4. Discussions and conclusions
4.1. Single-phase versus two-phases
The models discussed in this review suit both singlephased and two-phased permanent magnets. Particularly, the self-pinning coercivity mechanism was first proposed in twophased magnetic materials and then extended to single-phased permanent magnets. However, the comparison with the other experiments shows that the formula of the self-pinning agrees better with the single-phased materials. For example, the coercivity determined by the formula for Nd2Fe14B/Fe is 0.7 T,which is similar to the experimental data of many singlephased Nd2Fe14B without any particular coercivity enhancement. In addition, it has been discussed by Zhao et al.that,[10,25]Fe is very likely to occur in Nd2Fe14B such that many single-phased materials are in fact a two-phased one.Although these defects occupy very small volumes,they can deteriorate the coercivity significantly.It is evident from Fig.4,a 3-nm-thick planar soft defect can decrease the nucleation field and the coercivity by half.
To decrease the amount of soft Fe,the compositions used to manufacture the sintered magnets are generally Nd-rich and B-rich, rather than the stoichiometric composition R2Fe14B.Besides soft Fe, off-stoichiometric compositions were found to have smaller grains of the phase NdFe4B4irregularly distributed between the Nd2Fel4B grains.[1]Apart from NdFe4B4and the fcc Nd-phase forming part of the ternary eutectic,several investigations have reported the occurrence of the Laves phase NdFe2.[1]Recent investigations demonstrate that the thin grain boundary layer could be ferromagnetic,[49,76,77]supporting the theory of the self-pinning where the soft ferromagnetic phase is adopted in the model.
Experimental confirmation of this hypothesis in meltspun ribbons was also provided.[78-82]Particularly,it is found that the optimally quenched ribbons are two-phase materials.The grains of Nd2Fe14B(approximately 30 nm in size)are surrounded by a thin film of an amorphous phase, which is rich in Nd and deficient in B with an approximate Nd:Fe ratio of 7:3.
Therefore,many single-phased permanent magnets are at least a two-phased one from a micromagnetic point of view.By contrast, an artificially fabricated two-phased magnetic material is actually composed of multi-phases as each of the two phases are not really single-phase from a micromagnetic view. Consequently,the calculated coercivity based on a twophase model is usually larger than the experimental data.
Moreover, any poly crystals possess at least two-phases:one is the main phase and the other is the grain boundary. The grain boundary is usually a nucleation center as its local crystalline anisotropy is much lower than the main phase. Experimentally,an enhancement of the grain boundary may increase the coercivity of sintered Nd2Fe14B efficiently. This includes the addition of a heavy rare-earth element such as dysprosium and a non-magnetic element such as Cu.
Further, from a general point of view, a perfect single crystal without any structural defects may be a magnetically“two-phased”material unless it is a sphere or an ellipsoid. Reverse domains are usually nucleated at the corners and surfaces,forming a different magnetic phase in contrast to those in the center.
4.2. Pinning versus nucleation
The interface pinning model discussed in Section 3 indicates that the self-pinning is the dominant coercivity mechanism in the permanent nanomagnets. However,such a pinning does not exclude nucleation as aprerequisite for the formation of the reversed domains.
Most experiments infer that the dominant mechanism in the SmCo-type material is pinning,[73,83]while a few other experimental evidences indicate that the nucleation is also important in the magnetic reversal process. Therefore, self-pinning is considered as a governing reversal mechanism in SmCo material.
By contrast,most experimental observations made on the Nd-Fe-B-type materials indicate that the coercivity in the corresponding nanomagnets is nucleation-controlled[72,75]rather than pinning controlled, mainly because of the three reasons listed below.
(i) High low-field magnetic permeability values indicate that the domain walls can move easily,which is confirmed by the observations, suggesting there are a few pinning centers.This statement holds good for both sintered and melt-spun magnets. For sintered magnets,the grains are multi-domain at the thermally demagnetization state so that the domain walls can move freely within the grains. For melt-spun magnets, it is the easy motion of the multi-grain domain wall through the grain boundary that enhances the low-field susceptibility.
(ii) The coercivity of Nd-Fe-B and Pr-Fe-B magnetic materials is generally found to increase with the increasing magnetizing field.[84-88]As the applied field rises, the magnetic reversal becomes more difficult because of the constant removal of the residual reverse domains. These residual reverse domains behave as the nucleation centers, which facilitate the magnetization reversal and reduce the coercivity.
(iii)Most importantly,the measured coercivity is found to increase linearly with the anisotropy field Hain a quite large temperature region.
However, these three reasons also support the selfpinning mechanism.The high low-field magnetic permeability does not exclude the self-pinning mechanism from the demagnetization process,as the self-pinning is likely to occur at the grain boundaries and defects rather than the traditional pinning centers. Recently,Li et al.found that the mechanisms of the demagnetization and initial magnetization are different for nanocomposite permanent magnets,justifying the self-pinning mechanism.[89,90]In addition, a small amount of defects can provide efficient self-pinning according to the discussions in Section 3,where the theory is based on one single self-pinning center. Further,the increase in the coercivity with the applied field can be derived directly from the self-pinning mechanism as nucleation is the prerequisite for self-pinning. Most importantly,a linear relationship between the coercivity and the anisotropy field is reflected clearly in Eq.(12),the formula for the self-pinning field. Such a self-pinning mechanism is not only the dominant mechanism in the permanent nanomagnets such as melt-spun ribbons, but also determines the magnetic reversal in sintered magnets where the grain size is usually larger than 1 µm. An enhancement of the pinning centers at the grain boundaries can be made by the addition of nonmagnetic Cu,which can improve the coercivity clearly. Such an enhancement of the coercivity cannot be explained based on the nucleation mechanism, which, however, is in accordance with the self-pinning mechanism.
Furthermore, many experimental observations made by the means of electron microscopy confirm that the domainwall pinning at the grain boundaries is the reason for the high coercivity in the optimally quenched ribbons or in the over quenched and annealed ribbons. The same conclusion was drawn by Hilscher et al.[91]based on the minor loop behavior of these materials and by Pinkerton[1]based on the studies of the initial magnetization. In addition, the domain-wall pinning at the grain boundaries was reported for a variety of melt-spun materials of different anisotropy by Hadjipanayis et al.[92]using Lorentz microscopy. Recently, Zhang et al.found that the magnetic properties of the nanocomposites can be enhanced greatly by interface pinning and grain boundary pinning,suggesting a similar mechanism for the single-phased and composite permanent nanomagnets.[93-95]
4.3. Size effect and grain boundary enhancement
Another important issue in permanent magnets is the size effect and the related grain boundary enhancement of the coercivity. The grain diameter DGin melt-spun Nd-Fe-B is usually smaller than the single-domain particle diameter D0. However, DGexceeds D0in sintered Nd-Fe-B magnets.For this reason, many scientists concluded that the coercivity mechanism in melt-spun magnets is different from that in sintered magnets, along with the corresponding microstructures. However,it has been argued that every grain is a singledomain in the saturation state. Therefore, the difference in the coercivity mechanism of melt-spun and sintered magnets is not directly related to the single-domain size.
Several investigators found that the magnetic properties of melt-spun ribbons of a given composition depend on the quench rate,i.e.,on the wheel velocity V.[96-101]When plotted as a function of the wheel velocity V,the coercive force passes through a maximum at an optimum quenching rate(V0).
Thus, Croat et al. proposed that the peak coercivity corresponds to a grain size equal to the single-domain particle size. In under quenched ribbons(V <V0),the grains are larger than the optimum grain size, while in over quenched ribbons(V >V0),a large portion of the material is amorphous. Therefore,the coercive force is lower in over quenched than in under quenched ribbons,which is supported by the fact that the intrinsic coercivity of an NdFeB sintered magnet varies inversely with the grain size of the ultimate magnet. The grain size in sintered magnets is usually adjusted by the temperature and duration of the sintering cycle. Addition of dysprosium not only enhances the magnetocrystalline anisotropy,but also acts as an inhibitor for grain growth. Controversy still exists regarding the composition and structure of the intergranular layer. However,there is a general agreement that the nature of the intergranular layer is important in controlling the coercive force.
According to the self-pinning theory, the grain-sizedependent coercivity in sintered magnets is possibly due to the difference in the defect size.Larger the defect size,smaller the coercivity is.
The peak grain size is approximately 30 nm for melt-spun Nd2Fe14B,which is approximately one order smaller than that of the theoretical single domain grain size D0. The coercivity decreases for smaller grain size, which is well explained by the hybrid model proposed by Zhao et al.[18,19,102-104]The energy barrier for the motion of the transition region between the neighboring grains with different easy axes can be tunneled by the thermal activation within the hybrid model,when the grain size is smaller (approximately 10 nm for Nd-Fe-B). Therefore, the coercivity can be improved by the grain boundary pinning,which prevents the motion of the transition region.
There is a general agreement that the grain boundary pinning is important to obtain a high coercivity in both melt-spun and sintered Nd-Fe-B,which is consistent with the theory of self-pinning.
4.4. Conclusions
In summary,the study of the magnetic reversal,as well as the related coercivity mechanism has extensive technological applications in many nanostructured fields such as permanent magnetic materials,magnetic recording,and micromechanics.The micromagnetic models and the related coercivity mechanism such as self-pinning initially proposed for a hard/soft composite can be applied well to the so-called single-phased permanent magnets where defects are difficult to be excluded.
The underlying mechanism of the coercivity has been a topic of interest for many years in permanent magnets. It is motivated by the fact that the measured coercivity approaches only 20%-40% of the theoretical nucleation fields derived from the micromagnetic theory as developed by Brown and Stoner-Wohlfarth. Crystal defects are probably responsible for the lower measured coercivity. Therefore, two main approaches have been proposed to resolve this discrepancy. One is a micromagnetic approach while the other is a phenomenological“global”approach. Both methods can resolve the discrepancy by choosing the adequate parameters.However,their underlying philosophies are different. The micromagnetic approach can differentiate the reversal mechanisms,whereas the global approach cannot. Thermal activation effects are intrinsically considered in the“global”model,whereas they are neglected in the micromagnetic approach.
The simple SW model can give an explicit formula and a clear underlying coercivity mechanism based on the coherent rotation of the isolated grains. Such a model is exceedingly simple sometimes. However, it is widely used among experimentalists. By contrast, the key issue of the numerical investigations is to determine an accurate mimic of the domain wall, which can solve the problems with inherent geometric and physical complexity in principle. This approach,however,is sometimes exceedingly complicated, as it requires a large amount of meshes because of the thin domain wall of the permanent magnets.
In this review, the recently proposed self-pinning mechanism has been reviewed in detail, which can be applied to well-oriented permanent nanomagnets and sintered magnets.The self-pinning coercivity mechanism has the attributes of both nucleation and pinning,where a simple formula similar to the nucleation model can be derived. The pinning field arises from the magnetic property difference between the nucleation center and the main phase. Such a pinning is inherently linked to a nucleation center,which can explain the experiments supporting either the nucleation or traditional pinning.
- Chinese Physics B的其它文章
- Topological magnon insulator with Dzyaloshinskii-Moriya interaction under the irradiation of light∗
- Wavelength dependence of intrinsic detection efficiency of NbN superconducting nanowire single-photon detector∗
- Artificial solid electrolyte interphase based on polyacrylonitrile for homogenous and dendrite-free deposition of lithium metal∗
- Effects of CeO2 and nano-ZrO2 agents on the crystallization behavior and mechanism of CaO-Al2O3-MgO-SiO2-based glass ceramics∗
- Modulation of magnetic and electrical properties of bilayer graphene quantum dots using rotational stacking faults∗
- Thermal conductivity characterization of ultra-thin silicon film using the ultra-fast transient hot strip method∗

