考虑冲击力的球轴承外圈剥落缺陷双冲击现象动力学建模

罗茂林， 郭 瑜， 伍 星

(昆明理工大学 机电工程学院 云南省高校振动与噪声重点实验室，昆明 650500)

当滚动轴承内圈或外圈滚道表面出现局部剥落缺陷时，滚动体通过剥落区时会产生双冲击现象，针对该现象的研究对发展滚动轴承故障诊断理论及寿命预测方法有重要意义[1-3]。

Epps在研究中首先报道了轴承局部剥落缺陷对应的振动响应具有双冲击特征，即滚动体进入剥落区引起的振动响应呈现出阶跃响应特征，退出剥落区过程中与其后边沿撞击所激起的振动响应具有脉冲响应特征。并指出，若双冲击现象在时间序列上可观测，则可用其估计剥落区域大小。Sawalhi 等对滚动轴承外圈滚道剥落所引起的双冲击现象进行了较为深入的研究，并指出，通过准确检测进入与退出点所对应的时刻，可利用时差及转速等信息估计出局部剥落缺陷的尺寸。

但上述关于双冲击现象的研究都缺乏相关理论支撑。刘静等[4]考虑非线性Hertz接触特性和时变位移激励，建立了圆柱滚子轴承局部缺陷动力学模型。徐东等[5]对滚动轴承运转过程中承压滚子数变化规律的分析，采用分段函数和缺陷冲击函数描述滚动轴承运转过程中不同位置的缺陷是否处于承载区和缺陷产生冲击力的强弱，提出了单表面故障的滚动轴承非线性动力学方程。刘倩楠等以混合陶瓷球轴承外圈剥落故障为研究对象，通过构建剥落激起的时变位移函数与时变接触力增量函数，建立了滚动轴承外圈剥落故障动力学模型。但目前针对双冲击现象的动力学机理模型研究还较为鲜见，亟待发展较为精确的双冲击现象动力学机理模型。

本课题组在前期研究中取得部分进展，文献[6]基于剥落区附加位移分析，初步建立了滚动轴承外圈单一故障的双冲击现象动力学模型。本文对滚动体和剥落区接触的全过程进行分析，在前期研究基础上，提出了一种考虑冲击力的球轴承外圈剥落故障双冲击现象动力学模型。该动力学模型对合理阐释双冲击现象与剥落区长度的联系有重要意义，同时，基于双冲击现象的剥落区长度测量为运行工况下滚动轴承剥落损伤程度评价提供了崭新的途径。

1 双冲击现象产生原理

双冲击现象产生过程可用图1解释：径向载荷Q通过转子垂直作用在球轴承上(见图1(a))，设内圈以恒定角速度ωr回转。在球轴承承载区内，滚动体与内、外圈之间的接触区域可视为一椭圆面[7]；当滚动体进入剥落区时，其先与剥落区前边沿发生接触(见图1(b))；随着滚动体进入剥落区，轴承内部间隙变大，曲率半径变大，曲率和变小；由Hertz接触变形理论可知，接触力变小，导致去应力过程发生。该阶段，滚动体以与前边沿的接触点为回转中心做回转运动，其有一下落过程，同时受力逐渐减小，产生一阶跃响应，如图1(e)所示。在保持架带动下，滚动体到达剥落区中央，并与剥落区后边沿发生撞击(见图1(c))，产生一脉冲响应(见图1(e))；此后，滚动体以与后边沿的接触点为中心旋转至离开剥落区到达图1(d)位置时重新受力，应力恢复，如此往复。

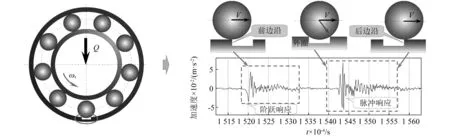
图1 双冲击现象原理图Fig.1 Schematic diagram of dual-impulse behavior

2 考虑冲击力的双冲击现象动力学模型

如图2所示，无故障球轴承在径向载荷Q作用下。在载荷区内，第k个滚动体与内、外圈之间相互接触挤压所产生的总接触形变dk分别为滚动体与内、外圈在接触点处作用所产生接触形变的代数和，即

dk=δin+δou

(1)

图2 球轴承接触形变示意图Fig.2 Sketch of the contact deflection of the defect-free ball bearing with a radial load

式中：δin与δou分别为滚动体与内、外圈间的接触形变。由图2所示几何关系可知，dk可近一步表示为

dk=xcosθk+ysinθk-0.5Cd

(2)

式中：x与y分别为内圈在x和y方向的初始位移偏量；Cd为球轴承内部直径间隙；θk为第k个滚动体相对于x轴的角度位置，可由式(3)定义

θk=2π(k-1)/Nb+θ0+ωct

(3)

式中:θ0为设定的第一个滚动体相对于x轴的初始角度位置(见图2);Nb为滚动体数目;ωc为保持架角速度，由式(4)计算

(4)

式中:ωr为转子角速度;Db为滚动体直径;D为节圆直径;α为球轴承接触角。

2.1 局部剥落引起的位移激励

为简化研究，本文以外圈滚道单一剥落为例，并将该剥落简化为一矩形凹槽，且仅考虑剥落区宽度小于滚动体直径的情况。

如图3所示，在载荷区内，当滚动体靠近剥落区时，由于受到外载作用而发生微小弹性变形，其球心位置相较于非载荷区有所降低；当滚动体进入剥落区时，其球心位置相比于正常滚道而言因滚动体滚入剥落区而降低，产生附加位移Δd。虽然在此过程中，滚动体与滚道之间的弹性变形得到一定程度的恢复，但远小于Δd；当滚动体退出剥落区并进入正常滚道时，其恢复到与进入剥落区前的状态。在整个过程中，滚动体质心历经C1-C2-C3的位置变化，基于以上事实，采用半正弦函数建立时变位移激励模型。

图3 滚动体产生附加位移示意图Fig.3 Schematic view of the producing processof the additional displacement

(5)

式中:mod(·)为求余函数；Ls为剥落区沿滚道方向长度；θs为外圈剥落区中心相对于x轴的角度位置；φs为剥落区对应于外圈中心弧度大小的一半，可定义为

(6)

式中:Dou为球轴承外圈直径，基于以上分析，结合式(2)和式(5)，即可将球轴承外圈缺陷引起的时变位移激励引入到动力学模型中。则在载荷区内，第k个滚动体的时变位移激励为

δk=dk-λkΔd

(7)

式中:λk为判断第k个滚动体在载荷区内与剥落区接触的参数，可表示为

(8)

2.2 载荷区静力计算

研究中以球轴承为对象，其主要承受径向载荷，且载荷通过滚动体在内、外圈滚道之间进行传递，滚动体与滚道间的接触满足Hertz弹性接触理论。研究中，假定外圈固定不动，内圈随着转轴旋转，经转子施加一垂直向下的径向力，滚动轴承在径向载荷作用下的整体受力如图4。

根据球轴承几何结构，可知载荷区内(-Φ<φ<Φ)任意角度位置φ处滚动体受力为

(9)

式中：Qmax为在φ=0处载荷区内的最大载荷；ε为载荷分布因子；n为载荷-形变指数，对于球轴承n=3/2，对于滚子轴承n= 10/9。参数Φ，ε，Qmax的计算见文献[8]。

图4 载荷分布示意图Fig.4 Sketch of distributions of internalloading in statically loaded bearings

参照图4，由静态平衡条件可知，作用于轴承上的外载荷Q等于轴承所承受载荷Qφ的垂直分量，考虑到球轴承受力的对称性，即有如下关系

(10)

2.3 冲击力计算

如上所述，从滚动体进入剥落区到其与剥落区后边沿撞击的过程中，滚动体的速度会有一个急剧变化的过程，伴随加速度产生，从而激发冲击力，引起轴承振动。因此，动力学机理模型中应引入冲击力。本文在建立了球轴承外圈剥落缺陷双冲击现象动力学模型的基础上，将相关的冲击力引入到模型中，通过分析滚动体与剥落区内在的撞击过程，给出了冲击力的近似计算方法。

对轴承系统而言，冲击运动是其内部动能传递的过程，其持续时间相对较短。假设整个球轴承系统能量守恒，则在冲击前后系统的机械能恒定。以图5(a)中滚动体所在水平面为参考面，由机械能守恒有

(11)

式中:mb为滚动体质量;Ib为滚动体的质量惯性矩，可由式(12)求得

(12)

式中：V与ω分别为滚动体的线速度与角速度，由圆周运动理论可知

V=0.5Dbω

(13)

将式(12)和式(13)代入式(11)，整理可得

(14)

式中:ϑ为冲击角，定义为在x-y平面内滚动体中心与剥落区后边沿接触点间的连线与竖直方向的夹角，在ϑ很小时

sin ϑ≈ϑ

(15)

依据图5 (c)中的角度关系可知ϑ=ϑ1，即

(16)

因此，由三角函数倍角关系可知

1-cos ϑ=2sin2(ϑ/2)

(17)

图5 滚动体与剥落区撞击过程示意图Fig.5 Sketch of the striking process between the ball and the spall

参照关系式(16)，将式(16)代入式 (17)，即得

(18)

将式(18)代入式(14)，进一步可得

(19)

参照文献[9]，近似可得动态(冲击)力的计算式为

F=Cimpact(ΔV)2

(20)

式中:Cimpact为一常量，与冲击材质和冲击体的质量大小有关。

滚动体在保持架带动下，以速度ωr做圆周运动，当滚动体滚过剥落区的过程中，其与剥落区后边沿撞击所产生冲击力的强度与其自身运动速度以及所承受外部径向载荷(Qφ)大小密切相关。因此，由滚动体与剥落区后边沿撞击所产生的冲击力应该由两部分组成，一部分是由外部径向载荷作用而产生的静态分量Fs(Fs=Qφ)，另外一部分是由滚动体撞击剥落区后边沿所产生的动态分量(Fd)。故由式(20)可得

Fd=CimFs·(ΔV)2

(21)

式中：Cim为一常量，仅与冲击材质有关。

Fim=Fs+CimFs(ΔV)2=Fs[1+Cim(ΔV)2]

(22)

将式(19)代入式(22)，整理可得

(23)

式中:C为一常量，与冲击材料和滚动体直径有关。

3 考虑冲击力的动力学模型

3.1 模型简化

为便于分析球轴承故障机理，建立描述双冲击现象的动力学机理模型，将滚动体与内、外圈间的接触视为一弹簧-质量系统[10-11]，如图6所示。为此作如下假设[12-13]。

(1)滚动体由保持架固定并绕转子均布，转子视为刚性。

(2)轴承内圈与外圈分别刚性固定在转子与轴承座上，内圈与转子间为过盈配合。

(3)滚动体在无故障区时，其与内外圈接触过程作纯滚动，并忽略滚动体在运动过程中其惯性对转子-轴承系统的影响。

(4)接触力只作用在径向(沿x轴和y轴方向)，转轴的质量包括内圈的质量。

企业把客户聚集到公众平台，不定期向客户推送信息，让客户对企业的品牌认知度越来越深。把所有客户加到公众平台，建立联系，持续下来，发挥更好的效果，节省投放广告的预算。微信作为腾讯公司的两大社交软件之一，有着强大的社交性、便利的互动性，即使是在微信公众平台，用户也可以向企业反馈问题，并得到及时回复，而企业则能够通过微信公众平台向它的粉丝实时推送信息[3]。

(5)在滚动体运动过程中，其与内、外圈弹性接触过程所产生的形变与接触力间的关系满足Hertz弹性接触理论。

图6 简化的弹簧-质量模型原理图Fig.6 Schematic diagram of simplified spring-mass model

3.2 动力学模型

基于Hertz弹性接触理论，时变接触力可由式(24)计算。

F=Ktδn

(24)

式中:Kt为滚动体与内、外圈间总接触刚度系数，计算见Harris等的研究。

(25)

式中:Kin，Kou分别为滚动体与内、外圈间的接触刚度，计算见Harris等的研究。

(26)

(27)

式中:Σρ为曲率和；下标b-in和b-ou分别为滚动体与内圈、外圈之间的接触曲率和；Eeq为等效弹性模量；e为椭圆度参数；ξ1和ξ2分别为第一和第二类椭圆积分。参数Σρ，Eeq，e，ξ1和ξ2的计算式见Harris等的研究。

基于以上分析，参照Sunnersjö[14]模型，可得描述双冲击特征的时变位移与冲击力相耦合的滚动轴承动力学微分方程为

(28)

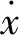
4 仿真及实验结果

4.1 仿真结果

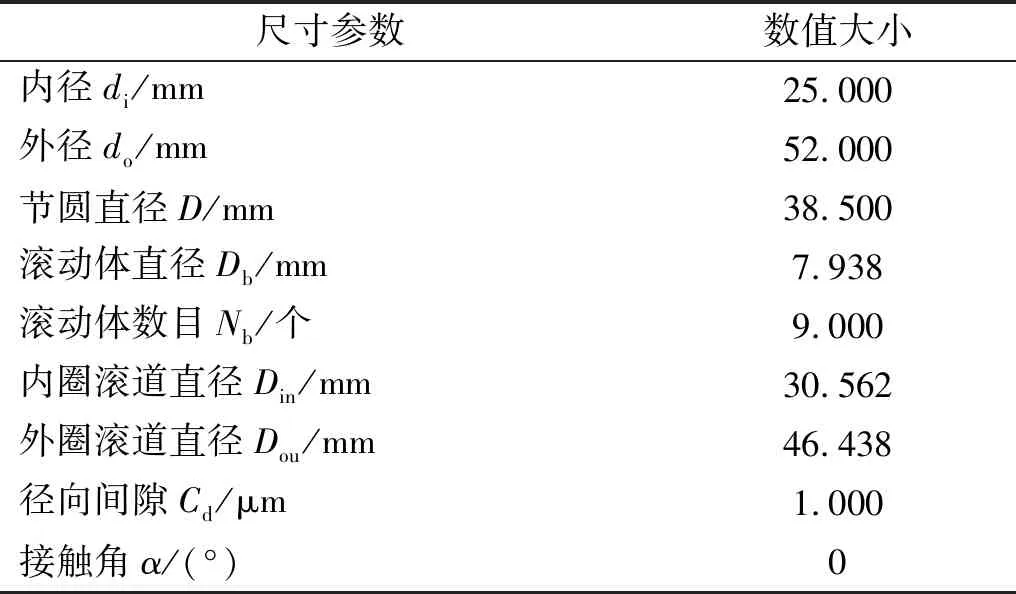
表1 混合陶瓷球轴承LYC 6205E几何尺寸参数

基于MATLAB软件进行编程仿真，运用定步长四阶Runge-Kutta数值积分法求解动力学微分方程，解得外圈故障仿真时域信号，如图7(a)所示。图7(b)对应双冲击局部细节展示，从中可看出仿真信号具有明显的双冲击响应特征。

图7 外圈剥落球轴承仿真信号Fig.7 Simulated signal of the ball bearing with a spall on the outer race

4.2 实验结果

为进一步验证文中所提出的球轴承动力学模型的合理性，以混合陶瓷球轴承(LYC 6205E)为实验对象，利用电火花方法在球轴承外圈滚道上加工出一个宽Ld=2 mm的损伤区域来模拟剥落故障，如图8(a)所示，并在QPZZ-Ⅱ旋转机械故障模拟实验台(见图8(b))上进行实验。试验中选用3个压电式加速度传感器进行振动信号的采集，其安装位置如图8(c)所示。

图8 实验装置Fig.8 Experimental set-up

研究中应用Autoregressive(AR)方法对实测信号进行预白化处理，以增强剥落球轴承的双冲击现象。图9为转速在442.58 r/min(fr=7.38 Hz)条件下采集到的外圈剥落所对应的振动信号双冲击现象。

如图5(b)，由圆周运动理论可知，滚动体从剥落区边沿1运动至边沿2的时间间隔，亦即振动响应中两冲击脉冲间的时间间隔Δt可定义为

(29)

联立式(4)、式(6)和式(29)可解得剥落大小为2 mm时对应的理论双冲击时间间隔。仿真、实测以及理论双冲击时间间隔对比如表2所示。

从表2中可知：在误差允许范围内，测量值与理论值基本一致。

图9 外圈剥落球轴承实测信号Fig.9 Measured signal of the ball bearing with a spall on the outer race

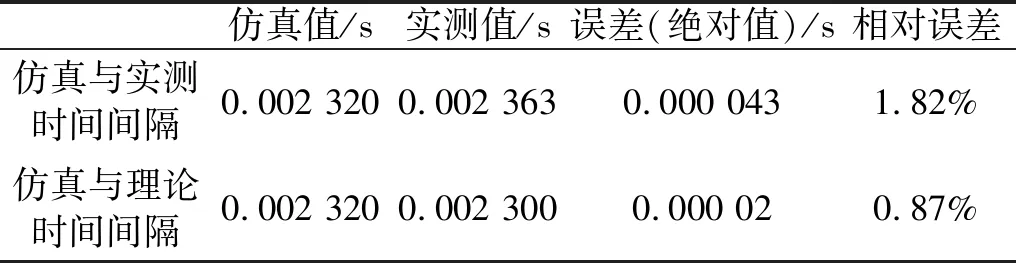
表2 仿真双冲击时间间隔与实测、理论值对比

为进一步验证本文所提出的考虑冲击力的球轴承外圈剥落缺陷双冲击现象动力学模型的有效性，对故障球轴承仿真信号与实测信号进行包络分析。图10(a)为未考虑冲击力的仿真信号包络谱，图10(b)为考虑冲击力的仿真信号包络谱。可发现在频率26.7 Hz处，图10(a)和图10(b)包络谱皆有明显峰值，通过对比可看出本文提出的考虑冲击力的动力学模型的优越性。与表3中外圈通过频率26.35 Hz以及图10(b)实测振动加速度信号中的26.35 Hz基本吻合，且存在明显的倍频成分(2倍频52.45 Hz和3倍频79.15 Hz成分等)。

表3 转速为442.58 r/min条件下 混合陶瓷球球轴承特征故障频率

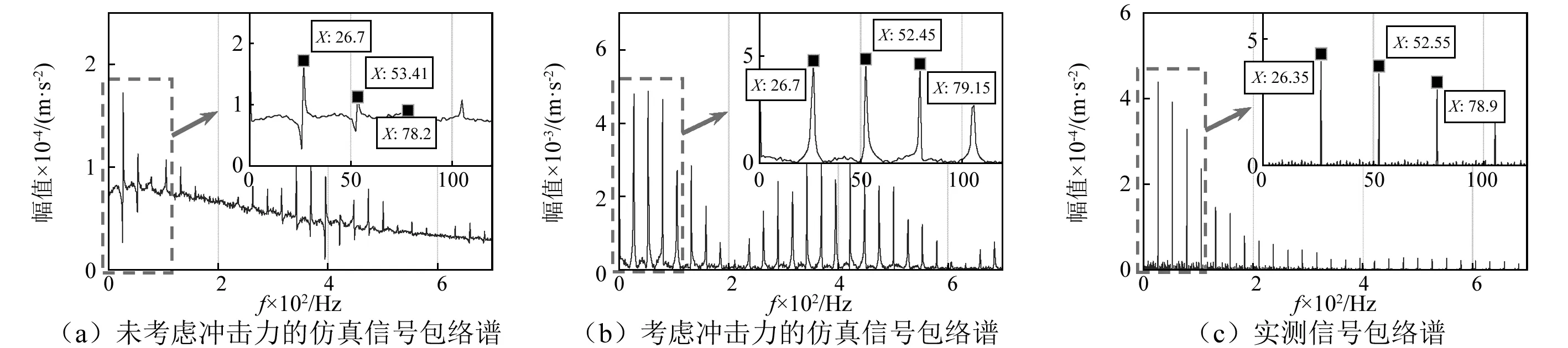
图10 仿真与实测信号的包络谱比对Fig.10 Comparison of envelope spectra between the simulated and experimental signals

5 结 论

本文基于Hertz弹性接触理论，通过分析滚动体位于载荷区内不同角位置与内、外圈滚道间的弹性变形量以及滚动体通过外圈滚道剥落区时所激起的时变位移激励并建立了相应的时变位移激励模型，结合球轴承结构参数与剥落区尺寸，将冲击力纳入考虑，建立了一种考虑冲击力针对双冲击现象的滚动轴承外圈剥落故障动力学机理模型。仿真、实测及理论双冲击时间间隔对比分析研究，并对仿真与实测信号进行包络分析。研究结果表明本文所建立的描述双冲击现象动力学机理模型的有效性。