层状盐穴难溶夹层爆破效应数值模拟研究

潘 越， 李二兵， 尤业超， 濮仕坤， 段建立，谭跃虎

(1.中国人民解放军陆军工程大学 国防工程学院，南京 210007；2.苏交科集团股份有限公司，南京 210017)

由于盐岩具有良好的低渗透性、蠕变性、损伤自愈性、易溶性等特性，深部盐矿水溶开采所形成的盐穴是国际上公认的石油、天然气等能源地下储备首选方式，已在美国、德国、法国、加拿大等国家广泛应用[1]，我国目前也在江苏金坛、江苏淮安、湖北应城、湖北潜江、河南平顶山等地规划了大量盐穴油气地下储库。我国盐岩矿床大多属于湖相沉积所形成的层状结构，硬石膏、泥岩和钙芒硝等难溶夹层较多[2]。在深部盐矿水溶建腔过程中，难溶夹层的存在不仅影响溶腔速度，导致腔体形状不规则，甚至突然垮塌给水溶建腔造成严重的安全隐患。研究表明，盐井聚能爆破技术不失为促使难溶夹层可控垮塌和消除建腔安全隐患的有效办法[3]。但由于盐穴地下储库需要满足稳定性和密闭性要求，盐井爆破一方面要促使难溶夹层可控垮塌，另一方面不能因爆破效应过大而影响整个储库密闭性，因此在开展现场先导性试验之前，进行爆破效应数值模拟分析显得十分必要和重要，更具有直接的工程指导意义。

目前，国内外针对岩体爆破数值模拟开展了广泛研究，肖正学等[4]根据室内试验和国内外矿山爆破的案例研究了不同初始应力对爆破作用的影响；谢源[5]研究了高地应力场对爆破裂纹的影响；袁青[6]基于不确定理论研究了花岗岩地下储气库洞室围岩爆破特征参量，获取了最佳特征参量预测模型；Chen等[7]研究了深埋隧道爆破开挖围岩损伤区与地应力关系；夏祥等[8]通过数值模拟研究了岩体爆破裂纹的产生和扩展机制，得到了粉碎区和裂隙区范围；孙金山等[9]在Flac3D中模拟了爆破应力波对邻近隧洞的动力扰动；郭文章等[10]基于DYNA-2D模拟节理岩体爆破过程，量化了节理岩体在爆炸荷载作用下的应力场；高科[11]进行了岩石SHPB试验模拟研究，证明了半正弦波加载方式是用于岩石类脆性材料大直径SHPB测试的理想形式；Zhu等[12]利用数值分析方法研究了动静组合加载SHPB试验过程中岩体的破坏和损伤特性，得到复合静力作用下岩石动强度增加机理；Zhu等[13]基于模拟分析手段探讨了轴压、围压等因素对岩石动态特性的影响；詹金武等[14]通过LS-DYNA模拟了破碎泥岩注浆结石体SHPB试验，验证了与试验结果吻合较好的HJC模型及其参数；李莹[15]借助LS-DYNA分析不同初始地应力场条件对爆破的影响，结果表明初始地应力对爆破作用影响在近爆区域较小而在远爆区域较大；张凤鹏等[16]借助有限元软件研究节理条件下岩体爆破机理，发现节理面产生的反射拉伸应力波加强了破岩效果。陈江海等[17]对洋山港水下爆破震动进行测试分析；陈春歌等[18]对水下爆破进行数值模拟，并提出了人工干预措施；王宏[19]模拟分析了水下钻孔爆破得到了水击波的传播规律。

上述分析可知，爆破效应数值模拟研究主要集中在隧道与地下工程、矿山边坡等领域。关于动载作用下盐穴稳定性研究分析很少[20]，且由于层状盐穴地质构造特殊性，盐穴内部注满卤水，使得上述研究不能直接运用。为此，本文首先进行三轴压缩状态下泥岩的SHPB室内试验，获得难溶夹层塑性随动硬化材料模型参数，利用LS-DYNA建立盐穴实例模型模拟分析泥岩夹层和盐穴腔体爆破振动等效应，以期为层状盐穴难溶夹层爆破方案设计和稳定性控制提供依据。

1 数值模拟模型建立

1.1 盐穴实例模拟背景

数值模拟实例为湖北应城某埋深1 000 m的层状盐穴，其存在厚度8 m的难溶夹层(主要成分是泥岩)，夹层上部盐岩层厚度约为90 m，夹层下部盐岩层厚度约为20 m。建腔过程中不断提升导管，使得溶腔由下而上逐层溶蚀，并在完成夹层下部盐腔溶蚀后即装药进行爆破(见图1(a)) 促使难溶夹层可控垮塌。保证形成的夹层通道畅通，加快建腔速度，并最终建成如图1(b)所示的盐穴储库。为简化溶腔建模，近似看作以距泥岩夹层底部上方21 m的点为圆心作半径29 m的球体并由泥岩夹层底面剪裁得到的下半部分。

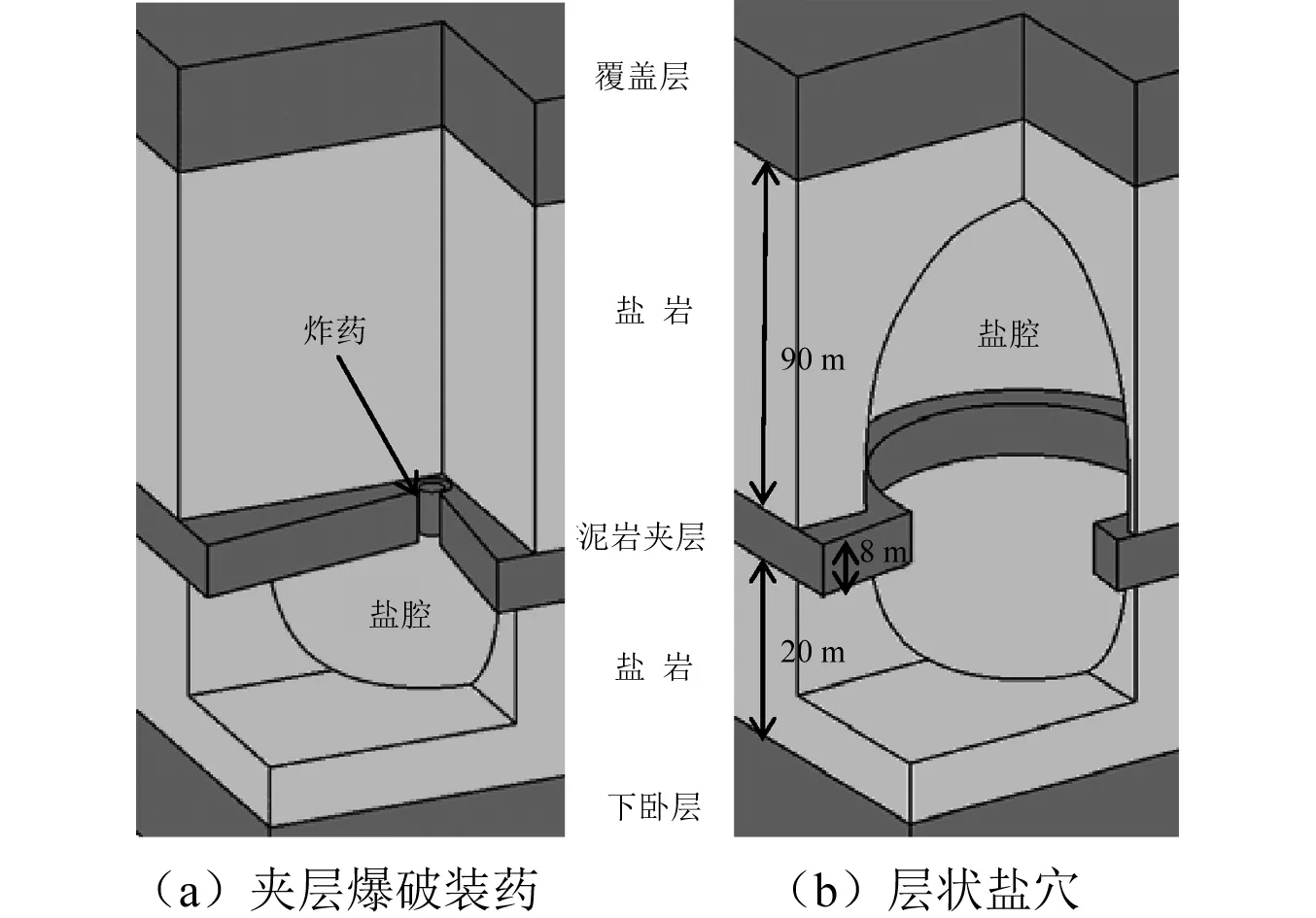
图1 层状盐穴爆破建腔示意图Fig.1 Schematic diagram of blastingconstruction of bedded salt cavern

1.2 动态力学试验装置

考虑到层状盐穴难溶夹层埋深约1 000 m，所处地应力约25 MPa。方秦等[21]通过三向压力下SHPB试验得出了盐岩的DIF随应变率变化曲线，得到了25 MPa下盐岩动态力学特性参数。因此，本文主要针对夹层泥岩进行围压25 MPa下的SHPB试验。

本次试验采用Φ75 mm带主动围压的SHPB试验装置(见图2)。装置主要由动力系统(提供初速度的氮气瓶和弹膛)、弹性杆件(子弹、入射杆和透射杆)、传感器(应变片、动态测速仪等)，入射杆和透射杆组成的压杆系统，长度分别为300 mm，3 500 mm和2 000 mm，材质均为高强度不锈钢，密度为7 850 kg/m3，弹性模量210 GPa。

1-入射杆端部液压油缸；2-试件环向围压装置；3-透射杆端部液压油缸；4-单作用液压油缸图2 带主动围压SHPB试验装置Fig.2 SHPB experimental device with confininge pressure system

1.3 试样制作及试验过程

本试验试件均采自湖北应城盐矿泥岩夹层，其主要成分为灰质泥岩平均含量为40%～50%，次要成分为CaSO4、Na2SO4和NaCl。

为了降低摩擦效应(试件与压杆之间的界面摩擦力)、惯性效应，使试验过程中试件能较好的满足均匀性假定，试件的长径比宜选为0.5。本试验选用Φ75 mm的压杆系统。为了使试件截面完全受压，在加工试件时，直径略小于压杆的直径(直径差不超过3 mm，否则导致数据失真)，因此，试验前将试件加工成标准尺寸Φ74 mm×37 mm，打磨过程实时进行平整度检查(见图3)，完成后，刷一层油漆，以防空气中的水分影响试件力学性能。选取5枚理想试样如图4所示，试样各物理特性及岩性特征见表1。

试验步骤：架设SHPB压杆系统，在压杆两侧架设提供反力的拉杆，冲击杆对中→架设围压系统→粘贴应变片、连接线路→在接触断面涂抹凡士林进行空打试验→加轴压空打试验→试样准备→三向压力下冲击试验，冲击气压分别设定为0.7 MPa，0.9 MPa，1.1 MPa→波形信号分析→数据分析处理。

(a)泥岩岩芯

(b)取芯及岩样打磨图3 泥岩试样制作Fig.3 Mudstone specimen making

图4 试样成品Fig.4 Specimens of the pre-test

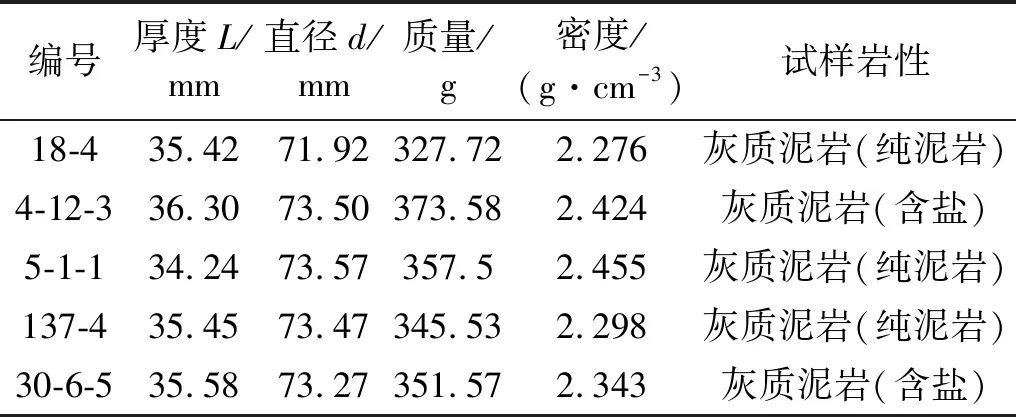
编号厚度L/mm直径d/mm质量/g密度/(g·cm-3)试样岩性18-435.4271.92327.722.276灰质泥岩(纯泥岩)4-12-336.3073.50373.582.424灰质泥岩(含盐)5-1-134.2473.57357.52.455灰质泥岩(纯泥岩)137-435.4573.47345.532.298灰质泥岩(纯泥岩)30-6-535.5873.27351.572.343灰质泥岩(含盐)

1.4 试验结果分析

将试验获得的电信号波形图数据导入SHPB数据处理软件，在平衡图中比较波与透射波近似重叠，说明试验过程满足SHPB试验应力均匀性假设，结果具有准确性。利用三波法处理数据并导出动态应力应变曲线，如图5所示，试验处理结果见表2。从图5和表2可知，试样具有明显的应变率效应，随着应变率的增加，峰值应力也普遍增加。

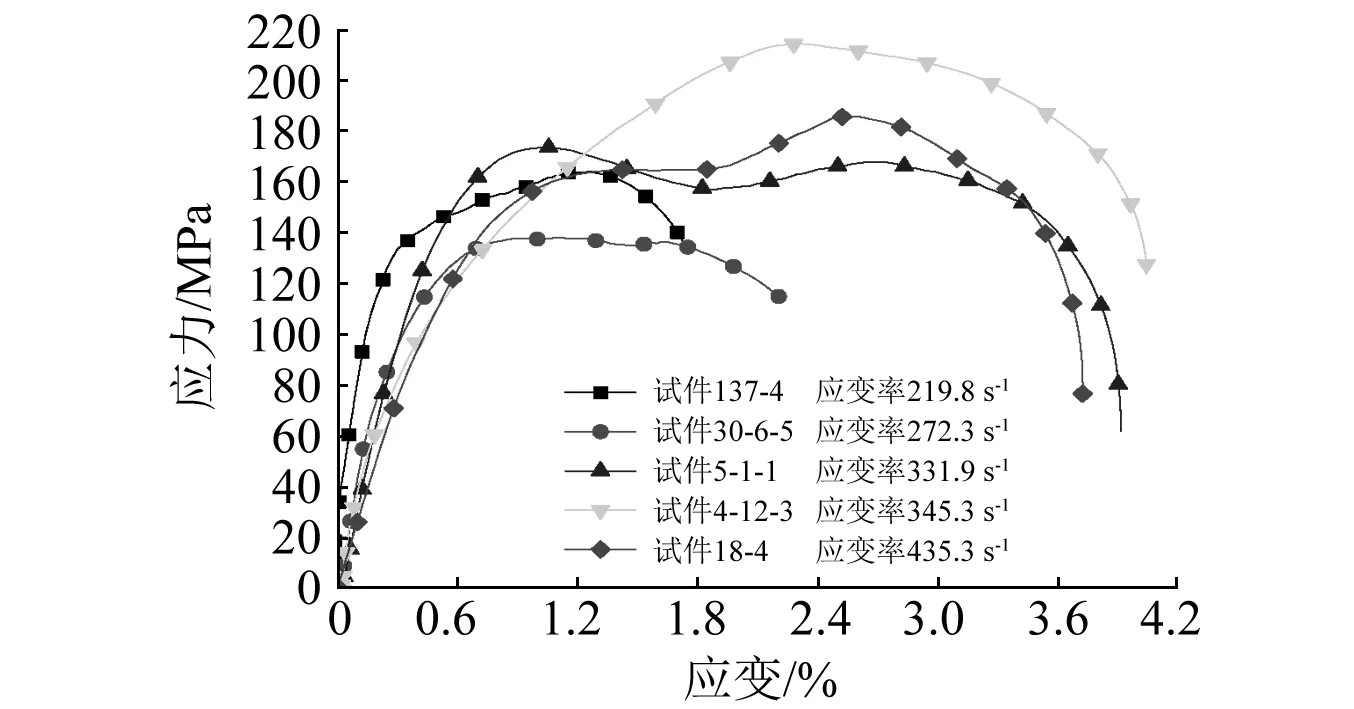
图5 泥岩夹层动态应力应变曲线Fig.5 Dynamic stress-strain curve of mudstone interlayer

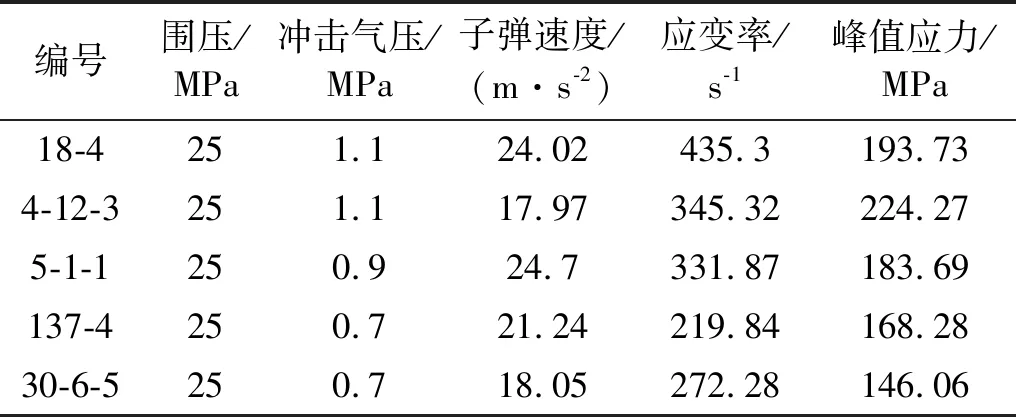
编号围压/MPa冲击气压/MPa子弹速度/(m·s-2)应变率/s-1峰值应力/MPa18-4251.124.02435.3193.734-12-3251.117.97345.32224.275-1-1250.924.7331.87183.69137-4250.721.24219.84168.2830-6-5250.718.05272.28146.06

1.5 模型参数验证

王健等[22]通过对不同围压下泥岩静态强度的拟合，获得25 MPa围压下泥岩夹层峰值应力为116.12 MPa。结合表2各应变率下峰值强度计算得到25 MPa围压下动力放大系数DIF(见表3)。

表3 25 MPa围压下泥岩夹层DIF

在LS-DYNA中采用非线性塑形材料模型(PLSTIC-KINEMATIC)可以反应应变率效应，并且模型简单，材料模型参数较易获取。岩石类材料的塑形屈服点与破坏点近似，故不考虑硬化，模型简化为Cowper-Symonds关系式

(1)

式中：σy为动态条件下的屈服应力(取峰值应力)；σ0为静态下的初始屈服应力；C和p为应变率效应提高系数。用Cowper-Symonds关系式对DIF进行拟合得到C和p参数值分别为254.4和1.7。根据应城泥岩夹层静态三轴试验结果[23]拟合得到25 MPa围压下静态力学参数，综合得到25 MPa围压下泥岩材料参数如表4所示。

表4 25 MPa围压下泥岩材料参数

在LS-DYNA中建立与SHPB实体试验相同尺寸的压杆模型(入射杆、透射杆长度分别为3 500 mm,2 000 mm；直径均为75 mm)，试件采用量取的尺寸。所有模型均采用Solid164单元。采用映射网格划分方法将入射杆沿长度方向划分350段，透射杆沿长度方向划分200段，沿杆半径方向划分32段。试件轴向分成48段，径向分成48段。整个系统为对称结构，为减少计算时间，建立1/4的模型进行计算(见图6)。为在接触面单元发生材料失效时剩余单元保持接触状态，压杆与试件之间采用面面侵蚀接触。另外，考虑到透射杆比较短，而波相对较长，在透射杆的端部加入非反射边界条件。对称面采用对称边界条件，入射杆自由端端部为应力边界(加载面)。

图6 SHPB模型及网格划分示意图Fig.6 SHPB model and grid partition schematic diagram

将试验测得的入射波作为冲击荷载施加在入射杆的端部可以避免入射波波形对计算结果产生影响。完成荷载施加后，设置接触、分析时间和能量控制等，通过调节材料模型参数获得模拟工况下的波形图，三波法处理得到模拟条件下的应力应变曲线。将数值模拟结果与SHPB实体试验结果比对(见图7)，大部分曲线与试验所获曲线较为接近，说明塑形随动强化模型可以较好地拟合泥岩动力特性，材料参数合理并可为后续爆破模拟提供参考。

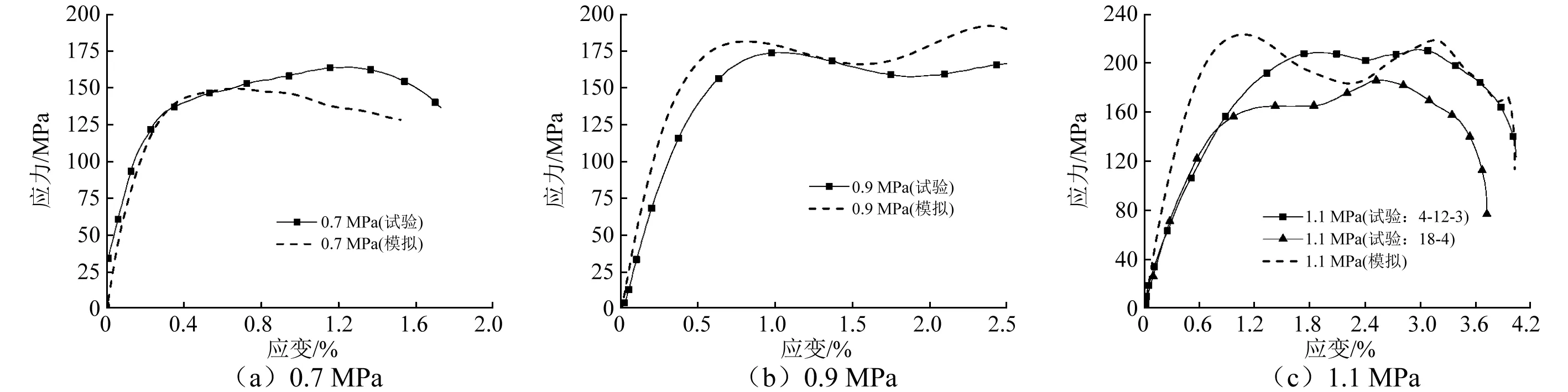
图7 围压25 MPa下模拟应力应变曲线与试验应力应变曲线Fig.7 Simulated stress-strain curves and experimental stress-strain curves under confining pressure of 25 MPa

1.6 材料参数确定

岩体材料模型均采用PLASTIC-KINEMATIC模型。上文对泥岩动力特性进行了研究和验证，用25 MPa围压下泥岩的塑性随动硬化模型参数填充泥岩夹层和下卧层材料；通过方秦等的研究，将25 MPa围压下盐岩的塑形随动硬化模型参数填充盐岩材料，如表5所示。

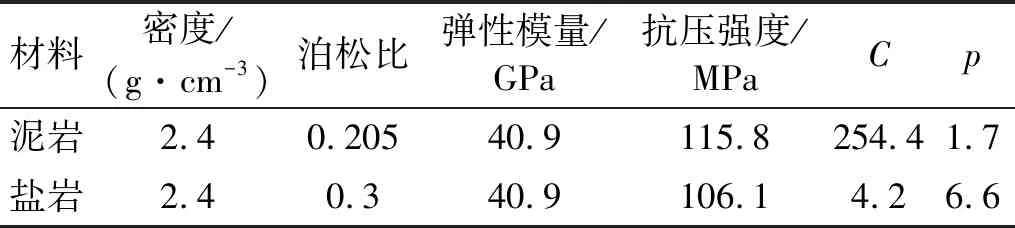
表5 岩体材料参数

炸药采用MATHIGH_EXPLOSIVE_BURN和EOS_JWL来描述高性能炸药的材料模型和状态方程。根据文献[24]，获得某高性能TNT炸药材料参数和状态方程参数，如表6所示。

卤水通常以低浓度注入，为了简化计算，卤水状态方程采用纯水的参数，而密度略大于水的密度，取值1.025 g/cm3。

表6 炸药材料参数

1.7 计算模型建立

在LS-DYNA中选用半径的3.5倍作为模拟的计算模型范围(模型半径90 m，高度100 m，见图8)，由于模型较大，内部结构并非线性尺寸，为了保证网格长短边尺寸之比满足计算要求同时达到计算精度要求，划分80万个单元，其中最小单元尺寸为0.5 m(指Lagrangian算法网格，ALE网格最小单元尺寸为0.2 m)。模型边界条件设为25 MPa应力边界，对称面设为对称边界条件。采用多物质流固耦合法(流体和固体不共节点)进行爆炸数值模拟，避免了Lagrange方法中因水和炸药产生大变形而导致的计算终止。

图8 数值模拟模型Fig.8 Numerical simulation model

2 数值模拟结果分析

2.1 夹层爆破试算分析

为了确定爆破的效果以及为后期装药量研究设置合理的计算梯度，先进行爆破试算。采用柱状装药，假设炸药半径为7.5 cm，高度6 m，重量为43.2 kg(为四分之一药柱的重量)，考虑到药柱下部为盐腔，为了降低端部爆破效应，同时充分利用炸药，炸药端部离夹层底部约1 m的位置。由于模型中液体压缩产生的冲击波会对爆破作用分析产生干扰，待计算到0.115 s后所有波形均耗散，整个模型应力趋于平稳。故在LS-DYNA中利用重启动将炸药起爆时间更改为0.15 s，研究0.15～0.2 s过程中的爆破波形图。依据文献[25]将振动峰值速度和等效应力作为两项重要的判据。

2.1.1 爆破作用下腔体围岩分析

考虑到盐腔围岩损伤过大会影响储库的密闭性，在盐腔围岩内壁上均匀选取平均弧长5.23 m的5个点A～E(见图9)。图10为各个点的有效应力和合速度的时程曲线。从图中可以看出，盐腔围岩各点有效应力变化较小、受冲击波影响小，故盐腔围岩的安全主要受振动速度控制。对比两图，可以明显看出E点距离药柱间距最大，但是最先受到爆破冲击的影响产生应力的变化和振动，而A点距离药柱端部仅9 m，却是最后受到爆破冲击的影响。分析可知，冲击波传递到盐腔围岩主要通过两种路径，一是通过钻井中卤水传递，而作用于盐腔围岩，另一种则是通过夹层岩体传递。应力波在岩体冲传播的速度明显大于在水中传播的速度。故出现了A点在爆破作用下的响应滞后于E点。从振动的绝对值来看，在该当量下，A点的振动峰值最大，为15.31 cm/s，其次是E点，为13.61 cm/s。其余各点受爆破作用影响较小，振动速度均不超过 5 cm/s。

2.1.2 爆破作用下夹层动力分析

为了对爆破作用下夹层动力响应有全面认知，在夹层下部和距离夹层底部高度4.5 m处分别布置观察单元F～I和J～M，上下对应的各点距药柱间距分别

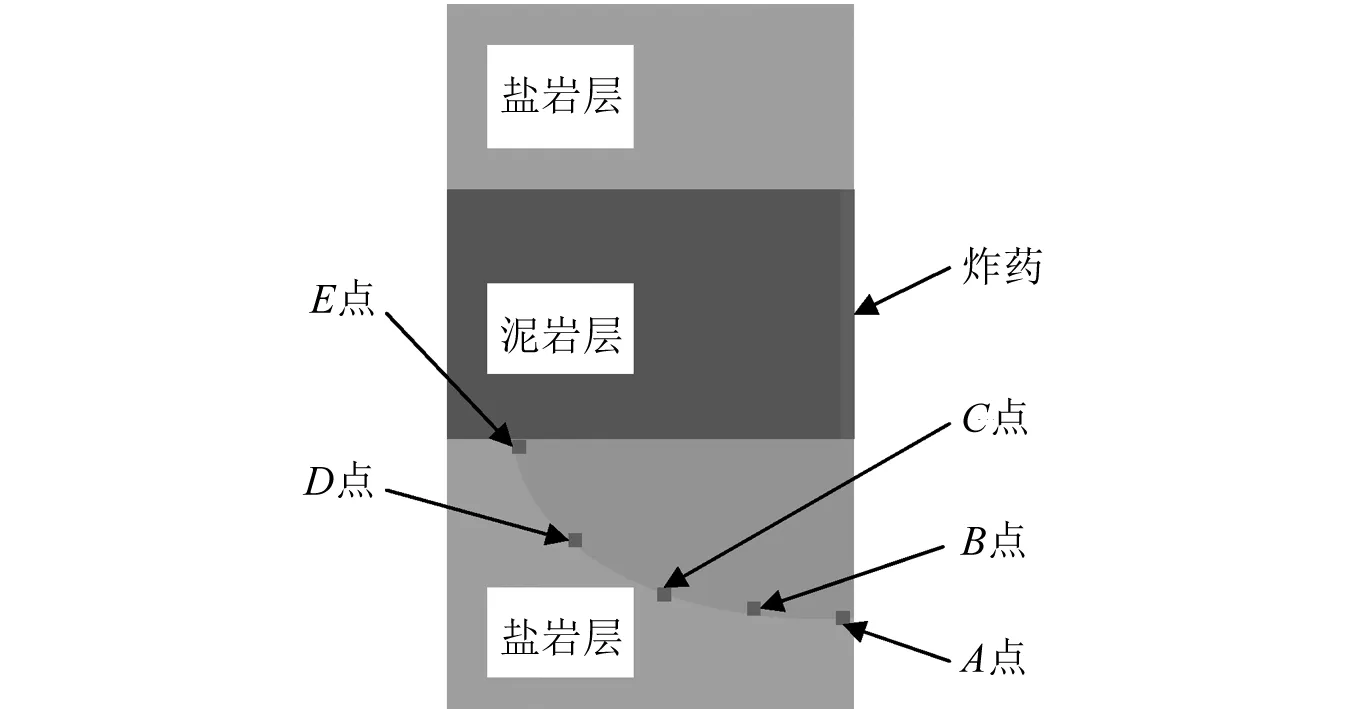
图9 盐腔围岩观察单元位置示意图Fig.9 Schematic diagram of the location of the observation unit of the surrounding rock of a salt cavity

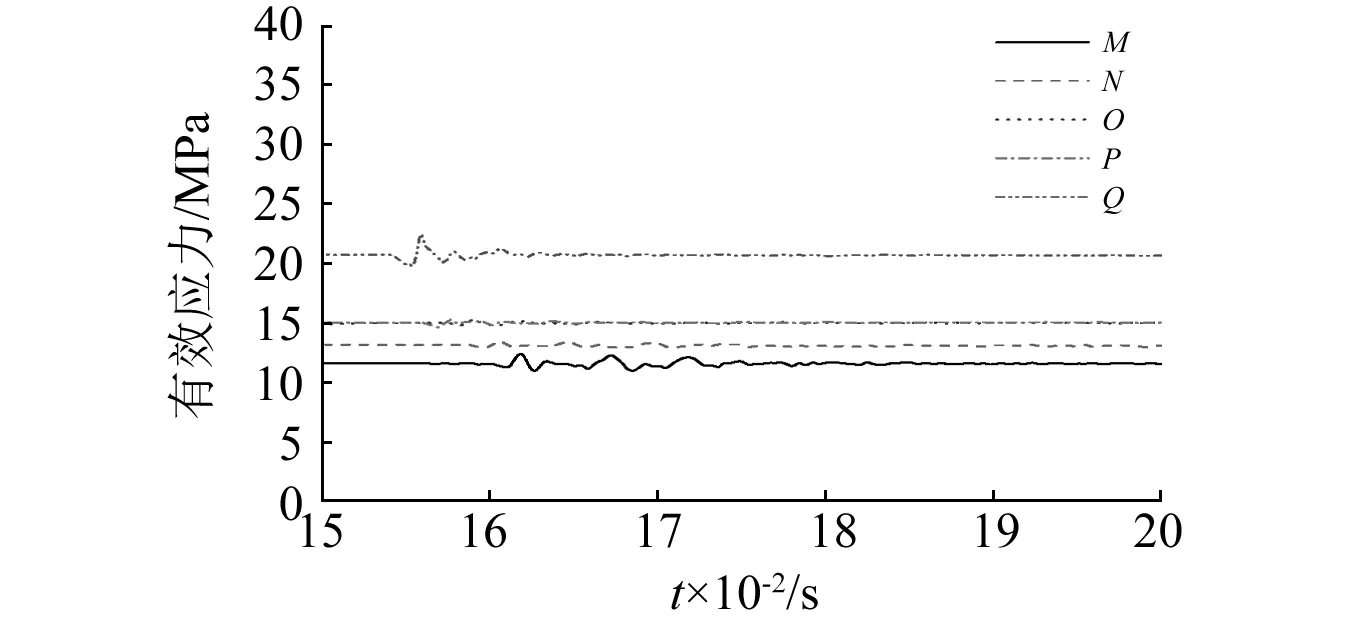
(a) 有效应力时程曲线

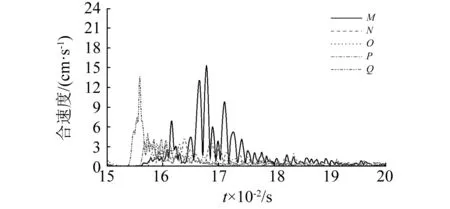
(b) 合速度时程曲线图10 盐腔围岩观察单元时程曲线Fig.10 The time history curve of the observation unit of the surrounding rock of the salt cavity

约为4.6 m，9.4 m，14.1 m和18.9 m。图11为夹层观察单元位置示意图。图12为各观察单元的有效应力和合速度的时程曲线。从图中看出随着与药柱间距的增大，应力波峰值和振动合速度峰值迅速降低。

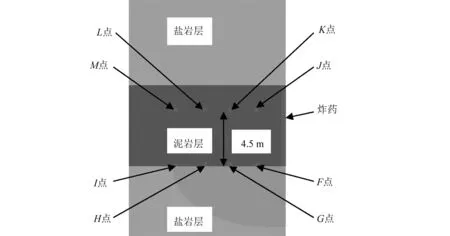
图11 夹层中部观察单元位置示意图Fig.11 Schematic diagram of the position of the observation unit in the middle of the interlayer

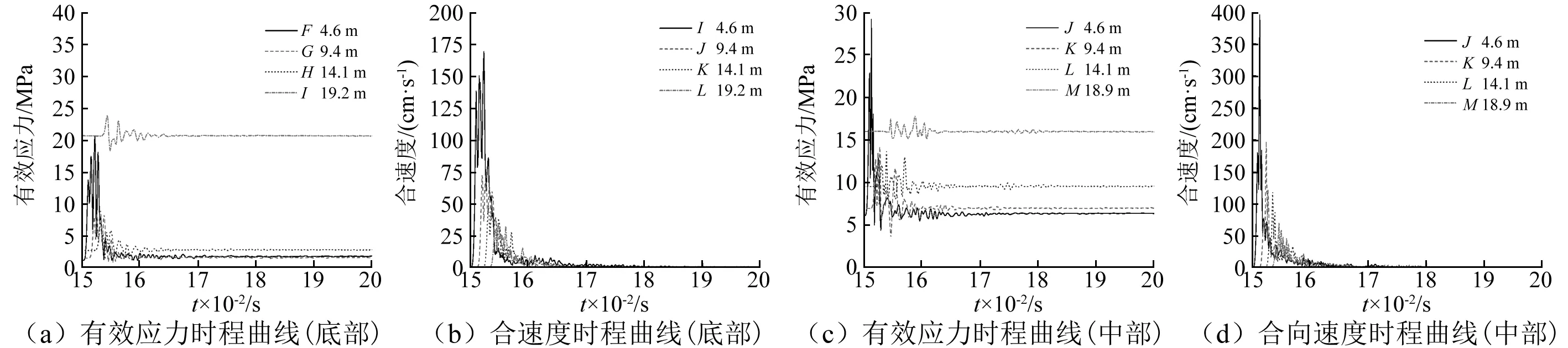
图12 夹层观察单元时程曲线Fig.12 Time history curve of interlayer observation unit

2.2 炸药当量对爆破作用的影响

为了探究炸药当量对夹层爆破产生的影响，依次选用4.8 kg，19.2 kg，49.2 kg和79.2 kg 4个当量(为四分之一药柱的重量)的炸药模拟对破坏效果的影响。根据3.1节所选的观察单元，提取爆破作用下各点的峰值有效应力和峰值振动合速度，并分析其与炸药当量的关系。图13为各观察单元峰值应力与炸药当量的关系。

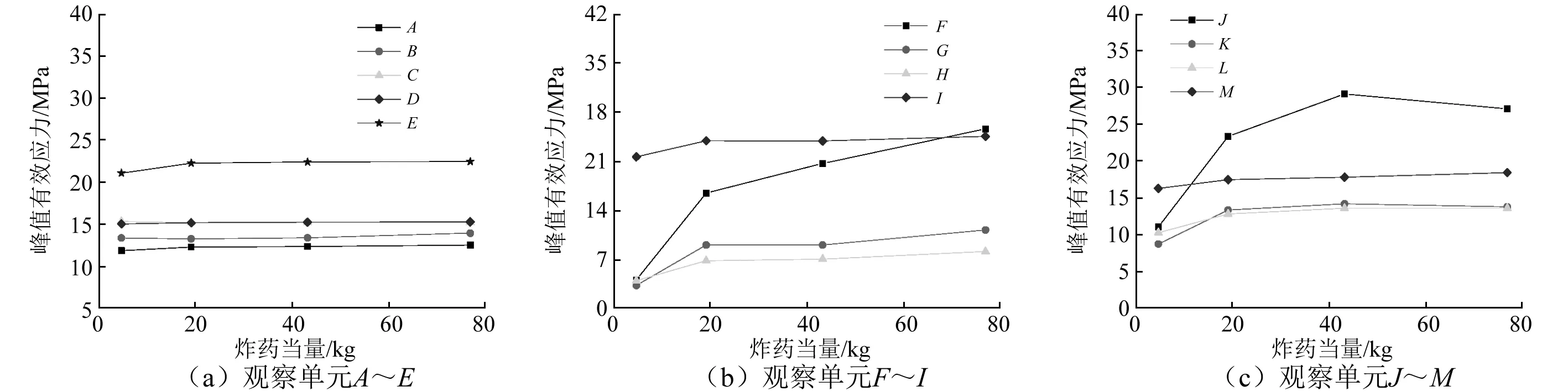
图13 观察单元峰值应力与炸药当量的关系Fig.13 The relationship between the peak stress of the observation unit and the equivalent of the explosive

从图中可以看出，随着炸药当量的增加，各观察单元的有效应力峰值一般都增加，但由于各测点的位置不同，其变化的规律也不尽相同。如图13中的A～E点，随着炸药当量变化，其有效应力变化很小，故而说明，爆破作用下炸药对盐腔的直接力学破坏作用小，可以忽略。另外，从图中可以看出，在离炸药较近的观察单元(如F点、J点)，其峰值有效应力受到爆破的作用影响较大，受到炸药当量的影响比较明显，而距离药柱越远，其峰值应力受到爆破炸药作用越小。

图14是观察单元振动合速度与炸药当量的关系，从图中可以看出，随着炸药当量的增加，同一个点的振动和速度也增加，距离药柱较近的位置速度增加的幅度大，较明显，而距离药柱远的位置，振动速度增加的幅度较小。图14(a)可以看出，盐腔围岩B，C和D振动速度受炸药当量影响较小，而A点和E点受炸药当量影响较大。图14(b)和图14(c)中反应距离效应比较明显，距离近的观察点随药柱当量的曲线在距离远的曲线之上，而在图14(c)中，A点和E点没有这个规律，其原因在于，岩石传播的波速及阻抗与水中传播的波速及阻抗不同。

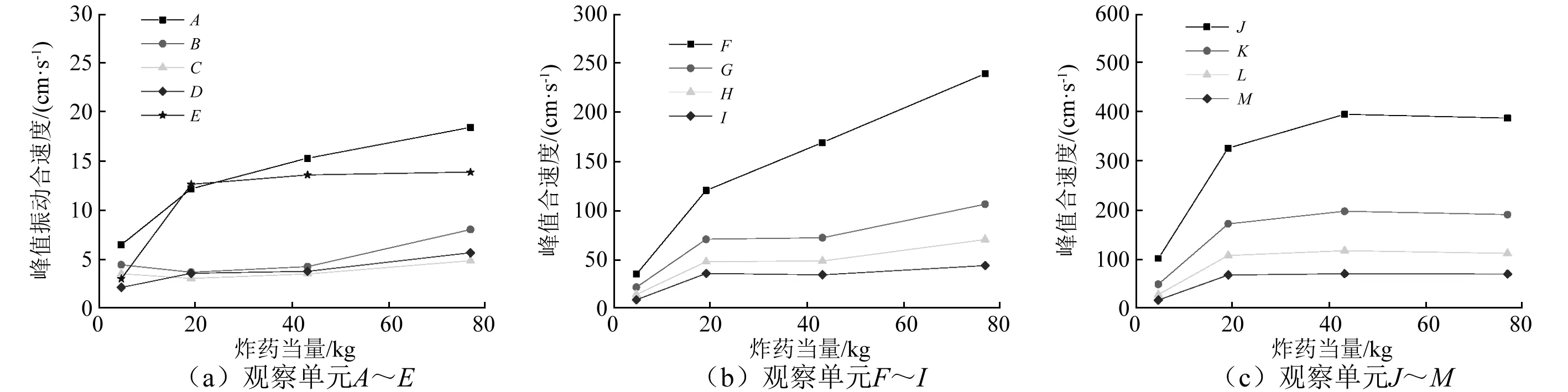
图14 观察单元振动合速度与炸药当量的关系Fig.14 Observe the relationship between unit vibration speed and explosive equivalence

2.3 炸药位置对爆破作用的影响

基于上部分计算结果，振动速度是爆破损伤范围的主要控制指标。选用半径7.5 cm，高度为6 m的炸药，药柱底端到夹层底部的距离直接关系到盐腔围岩的振动速度。为此，根据药柱下端面与夹层板底部的距离(分别为0 m，0.5 m，1.0 m和1.5 m)设置为4个工况。分别讨论药柱端部对盐腔围岩及夹层振动的影响。

图15为A～I观察单元围岩振动情况，从图中可以看出，药柱下端部与夹层的间距对围岩振动影响较大。随着药柱下端部与夹层的间距逐渐增大，A～D点的峰值振动合速度逐渐降低，主要是由于，药柱距离下端部的距离越小，药柱端部距离盐腔越近，冲击扰动就越大。另外，E点位于盐腔边缘部位，其峰值应力主要受到岩石中应力波传播的影响，而卤水传递的冲击波对其影响较小，故而随着间距的变化，其值变化相对较小。图15(b)中，随着距离增大，峰值合速度先增大后减小。主要是当间距为0 m时，夹层底部岩体主要受到冲击压作用，所以其振动速度较大。随着距离的增大，夹层底部在冲击波的作用下，会发生反射，从而提高了振动速度。当距离较大后，夹层底部受到冲击波和反射波都较小，故而其振动速度又发生降低。从H点和I点可以看出，观察单元距离药柱的绝对距离较大，其受到的冲击波和反射波均较小，药柱下端部与夹层的间距对其影响就相对较小，反映出来的速度变化就较小。

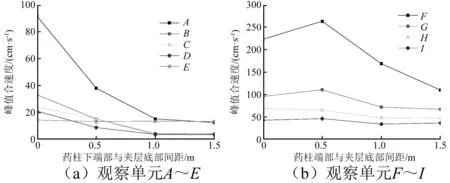
图15 药柱下端部与夹层底部间距对爆破振动的影响Fig.15 The influence of the distance between the bottom of the grain and the bottom of the interlayer on blasting vibration

2.4 爆破效应综合分析

爆破主要受两个因素控制，一方面，需要防止盐腔围岩损伤过大，影响盐腔的密闭性；另一方面，需要实现预期的爆破效果，获得理想的泥岩夹层破坏半径。由于岩石类材料抗拉强度远低于抗压强度，以抗拉强度为准则，根据简单的平面波估算盐腔围岩的振动速度承受范围，依此设定装药量和装药位置，验算夹层破坏是否符合预期效果。

(2)

式(2)可改写为

(3)

式中：V为岩石的振动速度；[V]为临界振动速度；c为应力波在岩石长传播的速度；[σt]为极限抗拉强度；E为弹性模量。

超声波在岩石中传播波速与围压的关系。考虑到应力波在岩石中传播波速与声波相近，此处引用超声波波速代替应力波波速，近似取4 350 m/s。

2.4.1 盐腔破坏控制

根据李二兵的研究，盐岩的抗拉强度为1.04 MPa。由于岩石的动态抗拉强度的应变率效应小，近似取动态抗拉强度等于准静态抗拉强度。根据获得的盐岩抗拉强度(直接拉伸强度)和盐岩的弹性模量，近似获取临界振动速度为16 cm/s。选取图9中各单元为盐腔破坏控制点。从图15(a)可以看出，A点受到药柱端部影响最大，且当药柱底部距离夹层底部距离大于1.0 m时，距离的影响变小。因此，药柱端部距离夹层底部1.0 m处为合理的安放位置。分析图14(a)可知，在药柱下端部距离夹层下部1 m时，装药量应控制不超过49.2 kg(为四分之一药柱的重量)。

2.4.2 夹层破坏控制

依据夹层破坏效应，为了充分反映夹层的破坏范围(包含爆破产生的直接效应和间接效应)，以使夹层产生裂缝为破坏标准，即夹层拉应力达到泥岩的抗拉强度。李二兵的研究给出泥岩抗拉强度2.19 MPa。为了更好的对计算结果定量分析，在模型图中选择高度4.5 m处水平面为观察面，如图16所示。在LS-DYNA中，以受压为负，受拉为正，故选择单元的最大主应力为观察项目，最大主应力达到极限抗拉强度，即认为夹层受拉开裂。

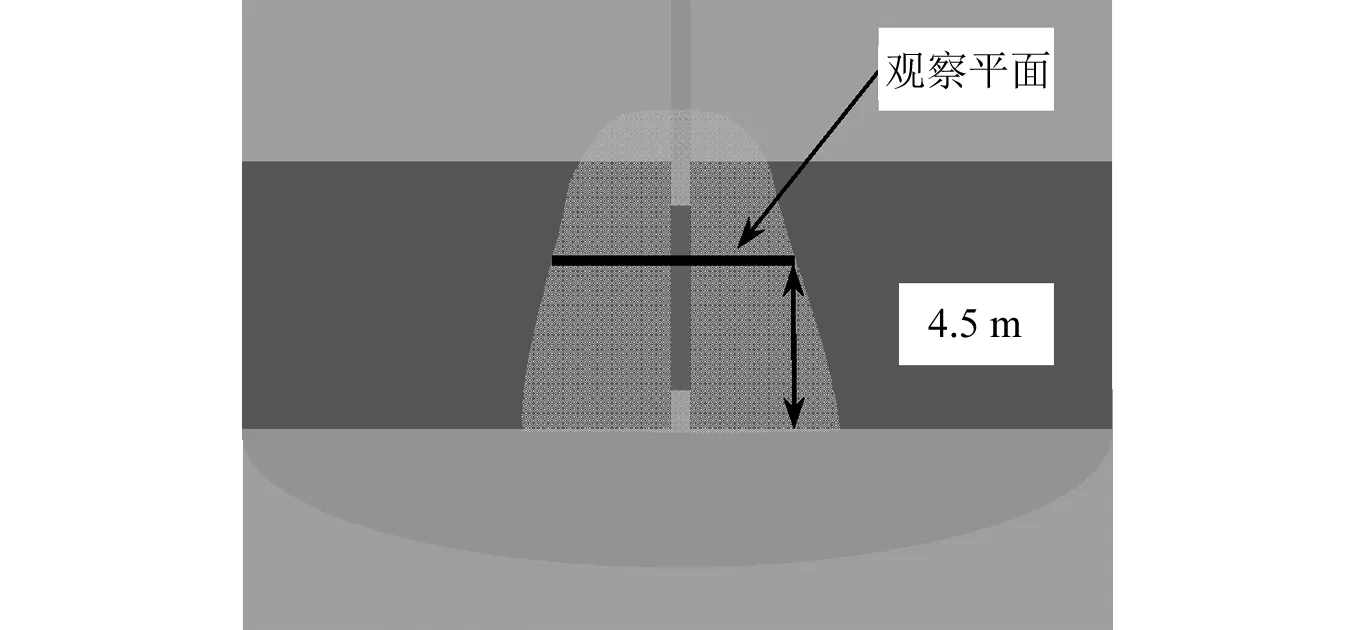
图16 破坏范围观察示意图Fig.16 Observation map of damage range

图17为破坏效果与装药量的关系。从图中可以看出，破坏效果与装药量有直接的关系，随着装药量的增加，破坏范围增大，但随着装药量增加，破坏半径增大幅度减小。按照四分之一装药量考虑，19.2 kg时破坏半径为8.66 m，49.2 kg时破坏半径为11.3 m，可见装量从19.2 kg增加1.56倍到49.2 kg，破坏半径仅从8.66 m扩大了0.3倍到11.3 m。难溶夹层厚度8 m，一般8 m左右的破坏半径足以满足难溶夹层可控垮塌要求。因此，难溶夹层爆破四分之一装药当量可选在19.2 kg左右，整体装药量约76.8 kg。

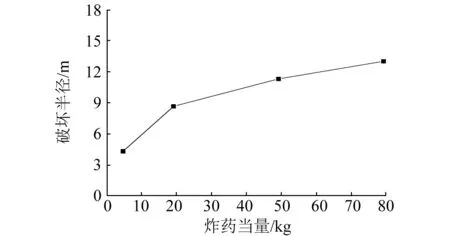
图17 破坏范围与装药量的关系Fig.17 The relationship between the range of damage and the amount of charge

3 结 论

本文通过SHPB试验获取难溶夹层材料参数。使用塑性随动硬化材料模型拟合，并使用LS-DYNA验证材料模型的正确性和模型参数的准确性。对盐穴实例建立数值模型进行研究分析，具体结论如下：

(1)在LS-DYNA中采用塑形随动强化模型可以较好地拟合泥岩动力特性，与25 MPa围压下SHPB试验结果具有较好的一致性。

(2)作用于盐腔围岩应力波通过卤水和夹层岩体两种介质传递，应力波在岩体冲传播的速度明显大于在水中传播的速度。

(3)通过对本盐穴实例进行数值模拟分析，为满足盐腔稳定性和密闭性的要求，若选取药柱半径7.5 cm，高度6 m，爆破炸药当量宜选在76.8 kg左右，并布置在药柱下端面与夹层板底部距离1 m的位置可以达到促使夹层垮塌的目的，同时保证盐岩溶腔围岩的气密性。