载流导线间轴向运动导电梁的参数-主共振

胡宇达， 张明冉

(1.燕山大学 建筑工程与力学学院，河北 秦皇岛 066004；2.燕山大学 河北省重型装备与大型结构力学可靠性重点实验室，河北 秦皇岛 066004)

随着科学技术的发展，复杂运动结构在航空事业、机械器件、电子设备等一些工程技术应用越来越广泛，例如，输送机的传送带、电磁发射、电磁驱动等设备中都含有轴向运动结构，这些轴向运动系统经常在电磁场环境中工作，受到机械场和电磁场的共同作用，所以电磁固体结构在多物理场耦合作用下的力学行为也引起了国内外学者的广泛关注。胡宇达等[1-2]针对磁场中轴向运动导电导磁梁及薄板的非线性磁弹性耦合振动的理论建模进行分析，从而推导出载流梁和薄板的磁弹性耦合振动微分方程；Ghayesh等[3]对具有纵向-横向耦合位移的轴向运动梁的强迫非线性动力学进行了数值研究，并推得了纵向-横向耦合运动的非线性偏微分方程；丁虎等[4]对轴向运动梁横向非线性振动的两组数学模型进行了研究。此外，针对梁和薄圆板的非线性振动稳定性及参数振动研究方面，Yang等[5]对由内部共振引起的稳态响应的非线性动力学现象进行了研究；Yurdda等[6]考虑非理想支撑情况，对轴向移动支撑弦的非线性振动问题进行了研究；Wu[7]对横向磁场和热负荷作用下梁的大幅度振动及动态稳定性进行了分析；Ding等[8]分析了轴向速度、边界条件等参数对结构振动频率及动力稳定性的影响；胡宇达等[9-10]研究了磁场环境中轴向变速运动导电矩形薄板和载流梁的磁弹性参数振动问题；Pratiher[11]对磁场中周期载荷作用下悬臂梁的主参数振动及稳定性等问题进行了研究；Ghayesh等[12]研究了轴向运动Timoshenko梁的双模态非线性参数共振；Tang等[13-14]针对Timoshenko梁模型，分析了随时间变化的轴向运动梁的参数共振现象及轴向加速黏弹性梁参数共振的动力学稳定性；Hu等[15-16]对磁场中轴向运动矩形薄板的非线性参数振动及稳定性进行研究，分析了磁场中轴向移动薄板的强非线性谐波共振和混沌运动现象。

本文针对两平行交变载流导线间轴向运动导电梁的参数-主共振问题进行研究，推导出轴向运动梁的非线性参数-主共振联合振动微分方程，分析平行导线载流强度和距离等参量对系统参数-主共振特性的影响。

1 载流导线间轴向运动梁的磁弹性方程

研究图1所示处在两平行交变载流导线间的载流导电梁，该梁沿形心轴x方向以速度c做轴向运动，并受轴向拉力F0x作用。梁的基本参数：长为l，宽为b，高为h，弹性模量E,质量密度ρ。导电梁通入的电流密度为J0x=J0，导线通入交变电流分别为I1(t)=i1cosωt和I2(t)=i2cosωt，导线与梁的距离为d1和d2，w(x,t)为梁的横向位移，t为时间变量，i1和i2为交变电流的幅值，ω为电流频率。

图1 载流导线间的导电梁Fig.1Conductive beam between current-carrying wires

利用毕奥-萨伐尔电磁定律[17]，可以得到两平行无限长载流导线在导电梁所在位置产生的叠加磁场之和为

(1)

式中：μ0为真空磁导率，当通入的电流i1cosωt与i2cosωt同向时取“-”,反向时取“+”。

由图1可知，当无外加载荷时，导电梁的磁弹性振动一般方程为

(2)

将式(1)代入电磁力Fz中，可得电磁力的展开表达式为

(3)

将式(3)用泰勒级数展开，忽略三次方及以上的高阶项，当载流导线通同向的交流电，可以得到导电梁的横向非线性振动微分方程

(4)

2 参数共振与主共振问题的解析求解

2.1 微分方程的伽辽金截断

当轴向运动梁受两端铰支约束时，考虑一阶模态情形，设满足两端铰支梁边界条件的位移解为

(5)

将式(5)代入式(4)中，进行伽辽金积分并无量纲化，可推得含变系数参数项和强迫项的非线性振动微分方程

(6)

2.2 多尺度法求解

研究系统参数-主共振问题，当应用多尺度法求解弱非线性方程式(6)时，需在方程等号右端引入小参数ε，即

(7)

为求解式(7)的近似解析解，选用两个时间尺度T1=τ，T2=ετ讨论系统参数共振和主共振方程的一次近似解，令其一次近似解为

x(τ,ε)=x0(T0,T1)+εx1(T0,T1)

(8)

将式(8)代入式(7)中展开，令ε的同幂次系数相等，得到各阶近似的非线性偏微分方程组

(9a)

(9b)

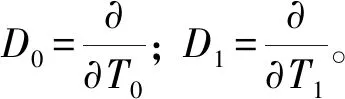
将零次近似方程式(9a)的解写成复数形式

(10)

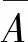
再将式(10)代入一次近似方程式(9b)的右边，得到

(11)

式中:cc为等号右端项的共轭复数部分。

分析式(11)可知，当激励频率与固有频率间满足一定关系时，系统可能出现不同形式的参数共振或主共振现象，下面分别进行讨论。

(1)Ω≈ω0情况

当激励频率与系统固有频率近似相等时，设Ω=ω0+εσ，其中σ为引入的频率调谐参数。由式(11)可知，为避免久期项出现，要求A满足

(12)

将复函数A写成如下指数形式

(13)

式中:a(T1),β(T1)均为T1的实函数。

将式(13)代入式(12)中，实部与虚部相分离，并令γ=σT1-β，得到关于a和γ的微分方程组

(14)

对于稳态运动的情况，令式(14)中a′,γ′都为零并且联立，可得关于系统参数-主共振的状态方程

(15)

由式(15)可知，对于系统的稳态运动解，即含有g7项的主共振激发项，也含有g1,g4,g6项的变系数参数共振激发项，因此，此时系统可能呈现主共振和参数共振同时存在的联合共振现象。

(2)Ω≈2ω0情况

当激励频率近似等于系统固有频率的2倍时，设Ω=2ω0+εσ，其中σ为引入的频率调谐参数。同理由式(11)可知，为避免久期项，必须令A满足

(16)

将式(13)代入式(16)中，实部与虚部相分离，并令γ=σT1-2β，得到关于a和γ的微分方程组

(17)

同理，对于稳态运动的情况，令式(17)中a′,γ′都为零可得幅频响应方程

(18)

当a=0时，式(18)成立，令式(17)中a′,γ′都为零，当a≠0时，将a消去并整理可得

(19)

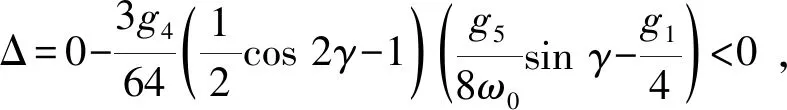
(20)

同理实部与虚部相分离，并令γ=2σT1-β，得到关于a和γ的微分方程组

(21)

对于稳态运动的情况，令式(21)中a′,γ′都为零可得幅频响应方程

(22)

当a=0时，式(22)成立，当a≠0时，将a消去并整理方程可得

(23)

通过对式(23)的解a2=x进行判断发现，根的判别式Δ<0，所以方程无非零实数解，故此时系统不存在非平凡稳态解。

3 算例分析

下面以轴向运动铜制材料导电梁进行算例分析。主要参数取值为：弹性模量E=108 GPa，质量密度ρ=8 920 kg/m3，导电率σ0=5.714 3×107(Ω·m)-1，真空磁导率μ0=4π×10-7H/m；梁长l=0.3 m，宽b=0.02 m，轴向拉力F0x=2 000 N，电流密度J0=2 A/mm2，导线与梁的距离为d1=0.04 m,d2=0.05 m。

图2 不同电流频率下的幅值变化图Fig.2 The curve of amplitude changes in different current frequency

图3～图5为利用龙格-库塔法求解式(14)，根据变化不同的初始值找到系统不同类型的奇点，再将不同调谐参数对应的奇点拟合成幅频响应曲线。

图3为i2=9 000 A，c=55 m/s，h=0.01 m时不同导线电流下的系统参数-主共振幅频响应图；图4为i1=10 000 A，i2=9 000 A，c=55 m/s时不同梁高下的系统参数-主共振幅频响应图；图5为i1=i2=9 000 A，h=0.01 m时不同轴向运动速度c下的系统参数-主共振幅频响应图。图3～图5中曲线中实心点代表稳定解，空心点代表不稳定解，从图中可知，随着εσ的增大，系统由单值逐渐变为多值解情况，且多值区包含稳定解和不稳定解；在给定εσ范围内，共振幅频响应曲线向右偏移，随着εσ的改变，曲线呈现硬弹簧特性，系统出现多值性和跳跃现象。

由图3可知，随着导线电流i1的增大，曲线的多值区右移，共振主架曲线呈明显的外扩趋势；由图4可知，随着高度h的增大，曲线多值区左移，共振主架曲线呈明显的内缩趋势；由图5可知，随着轴向速度c的增大，曲线多值区右移，共振主架曲线由狭窄的内缩逐渐变为外扩趋势。

图3 电流i1影响下的幅频响应图Fig.3 The curve of amplitude frequency in different current i1

图4 高度h影响下的幅频响应图Fig.4 The curve of amplitude frequency in different high h

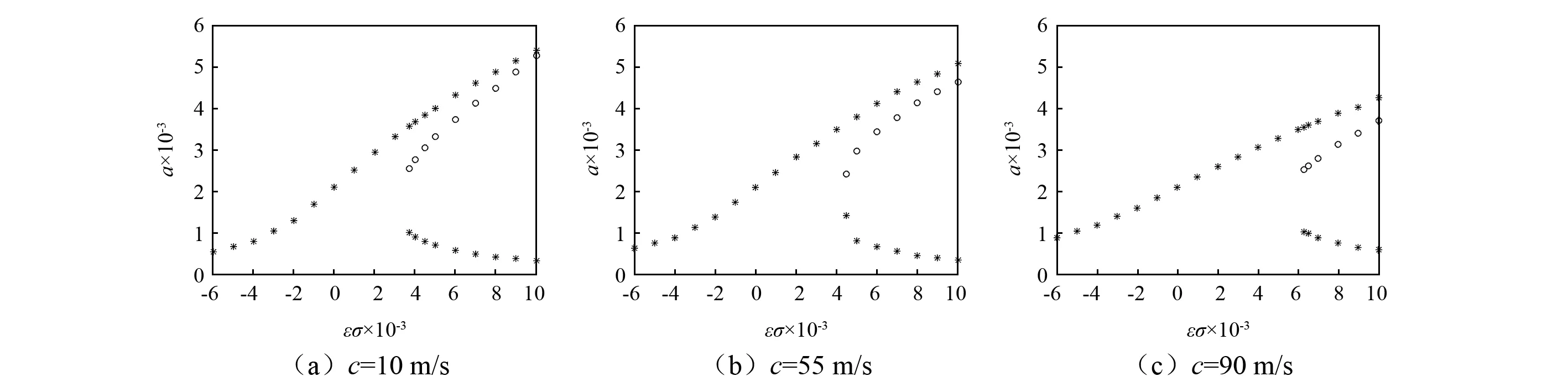
图5 轴向速度c影响下的幅频响应图Fig.5 The curve of amplitude frequency in different velocity c

图6～图14为运用龙格-库塔法求解式(14)，根据选取不同的初值，找到不同类型的奇点，绘制了变化导线电流、梁的高度以及轴向速度的动相平面轨迹图。

图6～图8为与图3对应得到的不同导线电流i1下的动相平面轨迹图。由曲线可知，随着调谐参数εσ的增大，由单值逐渐变为多值解，其中多值解中有一个不稳定解鞍点S2和两个稳定解焦点S1,S3，鞍点S2逐渐靠近焦点S3，逐渐远离焦点S1，与图3中的随电流变化的幅频响应结果吻合；随着电流的增大曲线逐渐由紧密变得疏松清晰，单值部分曲线形状发生变化，由圈绕比较圆润到圈绕形成类似椭圆形状。

图6 当i1=9 000 A时不同εσ对应的动相图Fig.6 The curve of dynamic phase trajectory in different frequency with i1=9 000 A

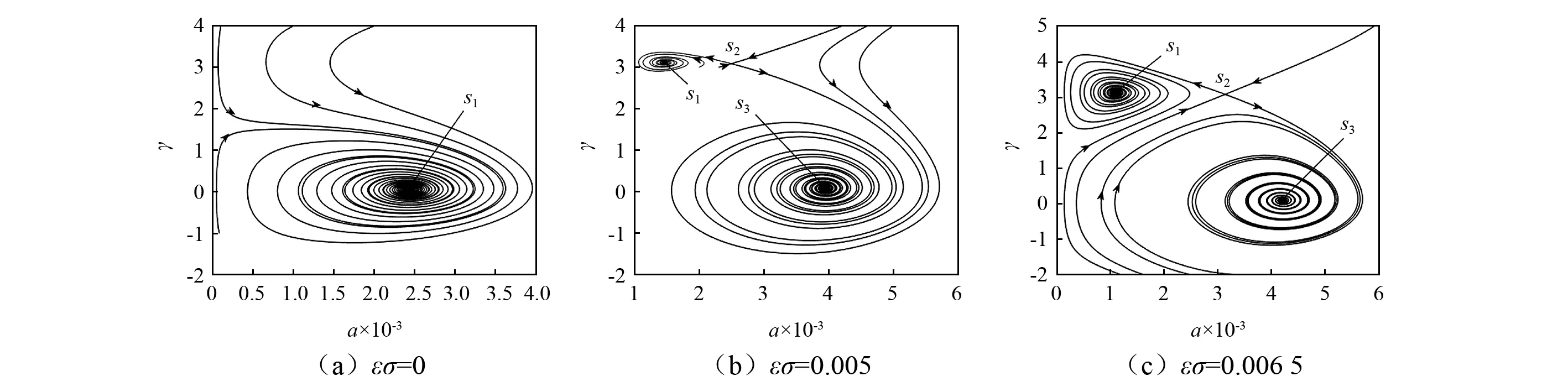
图7 当i1=10 000 A时不同εσ对应的动相图Fig.7 The curve of dynamic phase trajectory in different frequency with i1=10 000 A

图8 当i1=11 000 A时不同εσ对应的动相图Fig.8 The curve of dynamic phase trajectory in different frequency with i1=11 000 A

表1列出了与图6～图8对应的稳态解的具体数值，从表中可以看出，当εσ=0时，随着导线电流的增大，共振幅值也有增大趋势，但变化幅度很小；从数值上看单值解和多值解也与幅频响应图3中的对应值相同。

表1 不同导线电流i1下的幅值稳态解(×10-3)

图9～图11为与图4对应得到的不同高度h下的动相平面轨迹图。由曲线可知，随着调谐参数εσ的增大，由单值逐渐变为多值解，其中多值解中有一个不稳定解鞍点S2和两个稳定解焦点S1,S3，鞍点S2逐渐靠近焦点S3，逐渐远离焦点S1，与图4中的随高度变化的幅频响应结果相吻合；随着高度的增大，曲线逐渐由紧密变得疏松清晰，但单值部分的曲线圈绕形状基本没变。

图9 当h=0.01 m时不同εσ对应的动相图Fig.9 The curve of dynamic phase trajectory in different frequency with h=0.01 m

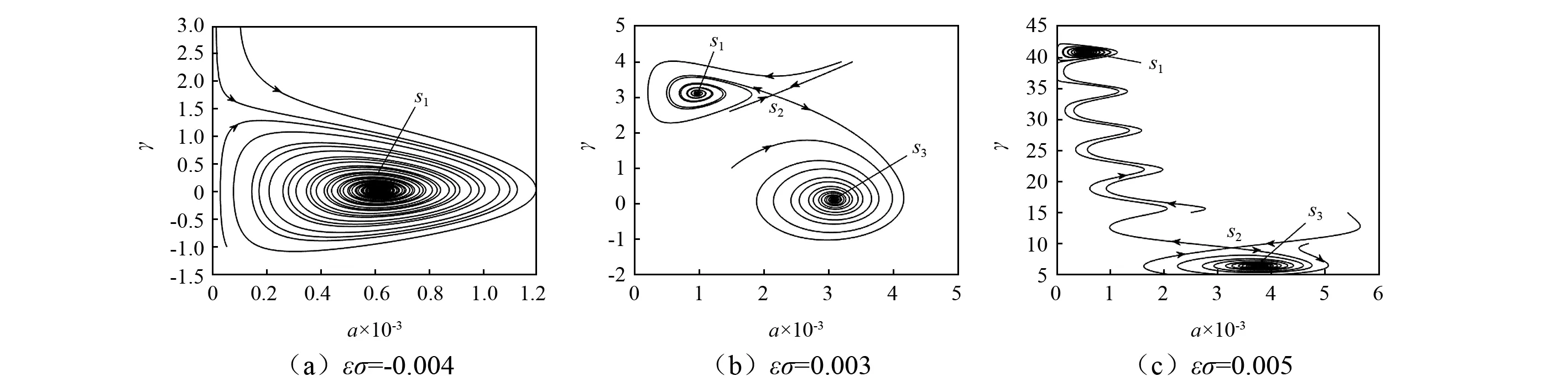
图10 当h=0.015 m时不同εσ对应的动相图Fig.10 The curve of dynamic phase trajectory in different frequency with h=0.015 m

图11 当h=0.02 m时不同εσ对应的动相图Fig.11 The curve of dynamic phase trajectory in different frequency with h=0.02 m

表2列出了与图9～图11对应的稳态解的具体数值，从表中可以看出，当εσ=-0.004时，随着高度逐渐增大，共振幅值逐渐减小；从数值上看单值解和多值解也与幅频响应图4中的对应值相同。

表2 不同梁的高度h下的幅值稳态解(×10-3)

图12～图14为与图5对应得到的不同轴向运动速度c下的动相平面轨迹图。由曲线可知，随着调谐参数εσ的增大，由单值解逐渐变为多值解，其中多值解中有一个不稳定解鞍点S2和两个稳定解焦点S1，S3，与图5中的随轴向运动速度变化的幅频响应结果相吻合；随着轴向运动速度的增大，曲线圈绕的紧密度及形状没有发生变化。

表3列出了与图12～图14对应的稳态解的具体数值，从表中可以看出，当εσ=0.002时，随着轴向速度逐渐增大，共振幅值逐渐减小；但变动幅度很小，从数值上看单值解和多值解也与幅频响应图5中的对应值相同。

图12 当c=10 m/s时不同εσ对应的动相图Fig.12 The curve of dynamic phase trajectory in different frequency with c=10 m/s

图13 当c=55 m/s时不同εσ对应的动相图Fig.13 The curve of dynamic phase trajectory in different frequency with c=55 m/s

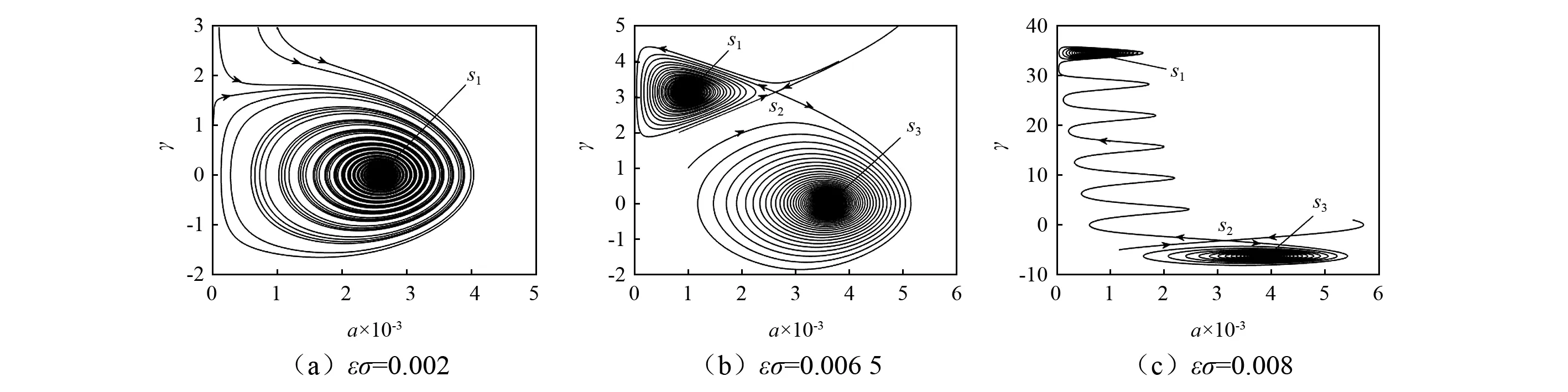
图14 当c=90 m/s时不同εσ对应的动相图Fig.14 The curve of dynamic phase trajectory in different frequency with c=90 m/s

轴向速度(c)调谐参数εσ0.0020.003 7S1S2S30.005S1S2S30.006 5S1S2S30.008S1S2S3c=10 m/s2.941.012.563.570.713.334.06c=55 m/s2.830.822.983.810.603.544.27c=90 m/s2.600.992.623.600.763.153.89

图15～图17为利用龙格-库塔法直接求解式(6)，初值选取为x=0.004，x′=0.000 6，绘制了与图3对应的不同导线电流i1条件下的时程图、相图。其中图(a)和图(b)为单值解情况，即一个稳态解，而图(c)和图(d)为多值解情况，即一个调谐参数εσ的值对应多个幅值，但是只有两个稳定解；且图中得到的数值结果与图3中的解析结果相吻合。

由图15和图3(a)可以发现εσ≈0.004 3为分界点；当εσ<0.004 3时，为一个稳定解，随着εσ的增大，幅值逐渐增大；当εσ>0.004 3时，逐渐出现两个稳定解，其中幅值较大的随着εσ增大而增大，幅值较小的随着εσ增大而减小；通过比较数值解与解析解发现，当εσ=0.004,εσ=0,εσ=-0.004时，图15(a)中所对应的幅值大小与图3(a)中幅值相吻合，当εσ=0.004 5时，图15(c)中的两个解的大小与图3(a)中的上下两个稳定解相吻合。

由图16和图3(b)可以发现εσ≈0.004 75为分界点，当εσ<0.004 75时，为一个稳定解，随着εσ的增大，幅值逐渐增大；当εσ>004 75时，逐渐出现两个稳定解，其中幅值较大的随着εσ增大而增大，幅值较小的随着εσ增大而减小；数值解与解析解比较发现，当εσ=0.004,εσ=0,εσ=-0.006时，图16(a)中所对应的幅值大小与图3(b)中幅值相吻合，当εσ=0.006时，图16(c)中的两个解的大小与图3(b)中的上下两个稳定解相吻合。

由图17和图3(c)可以发现εσ≈0.006 35为分界点，当εσ<0.006 35时，为一个稳定解，随着εσ的增大，幅值逐渐增大；当εσ>0.006 35时，逐渐出现两个稳定解，其中幅值较大的随着εσ增大而增大，幅值较小的随着εσ增大而减小；比较发现，当εσ=0.006,εσ=0,εσ=-0.004时，图17(a)中所对应的幅值大小与图3(c)中幅值相吻合，当εσ=0.007时，图17(c)中的两个解的大小与图3(c)中的上下两个稳定解相吻合。

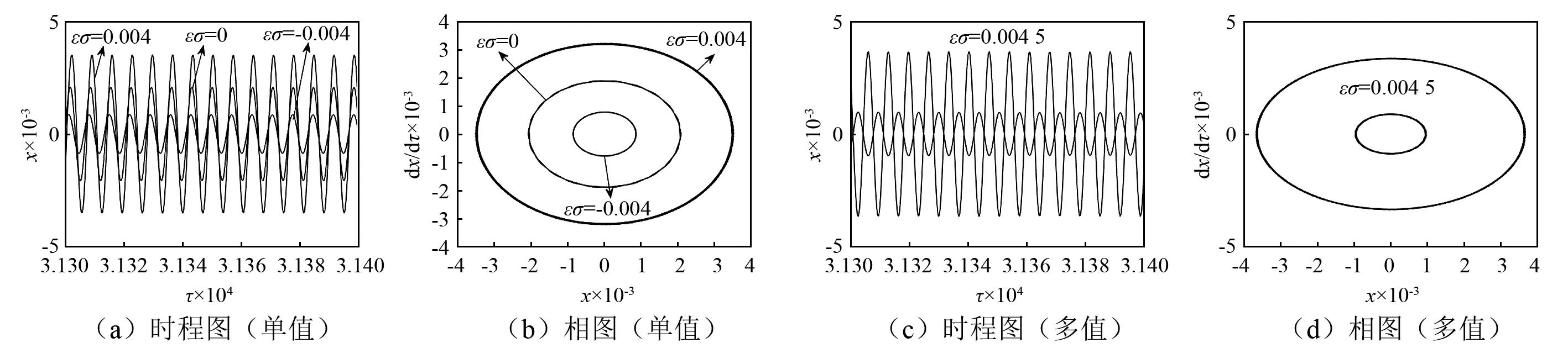
图15 当i1=9 000 A时不同εσ对应的时程图和相图Fig.15 The time history response diagrams and phase plot in different frequency with i1=9 000 A

图16 当i1=10 000 A时不同对应的时程图和相图Fig.16 The time history response diagrams and phase plot in different frequency with i1=10 000 A

图17 当i1=11 000 A时不同εσ对应的时程图和相图Fig.17 The time history response diagrams and phase plot in different frequency with i1=11 000 A

4 结 论

本文针对载流导线间轴向运动导电梁的参数-主共振问题，推导出不同激励电流频率下磁弹性参数-主共振状态方程，并判断了非零稳态解的存在情况。算例计算结果表明：

(1)轴向运动梁的幅频响应曲线具有多值性和跳跃性现象，呈现硬弹簧特性，具有复杂的非线性动力学行为。

(2)从动向平面轨迹图中可以看出，随着调谐参数εσ的增大，出现两个稳定焦点一个鞍点，且鞍点S2逐渐靠近焦点S3，逐渐远离焦点S1，其值与幅频响应曲线中对应的计算结果相吻合。

(3)从时程图、相图中可以看出，通过改变不同的调谐参数，幅值大小变化规律与动相图和幅频图保持一致，验证了解析结果的正确性。