基于VERICUT的变螺距螺杆多轴数控加工仿真研究*
董朋莎,孙会来
(天津工业大学 机械工程学院,天津 300380)
0 引言
随着零件结构和加工工艺的日益复杂,现代数控技术朝着高精度高效率的方向高速发展。复杂曲面类零件在多轴数控机床上加工时,有时会出现干涉和碰撞等现象,造成工件、刀具甚至是机床的损坏[1]。所以,在加工这些复杂零件之前,一般都要对其进行试切加工,对加工程序进行反复调试,寻求最优化方法,这样就大大降低了零件的加工效率,提高了加工成本。
变螺距螺杆由于曲面复杂,导致其加工工艺繁琐,加工难度较大,且目前多采用螺杆专用机床进行加工,在普通机床上实现变螺距螺杆的加工,是异型螺杆加工领域的一个重要方向[2]。
为了解决上述问题,本文根据空间无瞬心包络铣削原理,通过对变螺距螺杆螺旋曲面插补算法的研究和刀具刀位点的求解[3-5],编程得到了螺杆的5轴数控加工程序,并以DMG DMU80T型5轴机床为原型,采用虚拟制造及数控加工仿真软件VERICUT进行加工仿真,该仿真可以在保证刀具轨迹的正确性的前提下,避免干涉和碰撞现象的发生,可以代替螺杆在实际加工中的试切过程,提高加工的效率和安全性,为螺杆的实际加工生产提供指导。
1 数控加工仿真模型的建立
本文是对多头变螺距螺杆精加工过程的仿真研究,故使用Solidworks软件建立的螺杆精准模型作为“设计”件,刀具对螺杆的切削过程本质上是VERICUT软件内部进行的布尔减运算,所以暂不考虑刀具磨损以及机床加工热误差等因素;同时精加工是基于成型盘铣刀的空间无瞬心包络铣削加工,不涉及换刀的过程,故不存在刀具位置补偿和长度补偿 。
1.1 五轴机床模型
变螺距螺杆的加工需要螺杆绕自身轴线转动,同时为了适应螺杆不断变化的螺旋角,刀具安装角也随之变化,故需要在四轴联动或者更高的机床上实现。
本文选择的是摆头转台型5轴机床DMG DMU80T,由于VERICUT软件三维建模功能的局限性,故根据机床的实际尺寸和组件之间的位置关系用Solidworks软件创建机床模型组件,根据机床的实际运动结构,导入VERICUT软件中正确设置项目树中各组件的坐标系位置和运动方向[6],添加控制系统为Heidenhain iTNC 530,得到的五轴机床模型如图1所示。
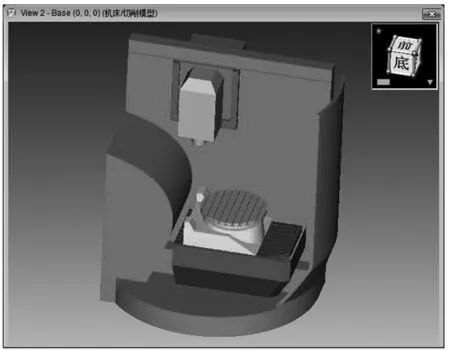
图1 DMU80T 5轴机床模型
1.2 刀具刀柄模型
空间无瞬心包络铣削法由于其高效率、高精度等优点被广泛应用于异型螺杆的加工。在切削加工过程中,成型盘铣刀刀盘的高速旋转为主切削运动,切削刃的回转表面为双锥面过渡的圆环面,将刀具模型简化,如图2所示。
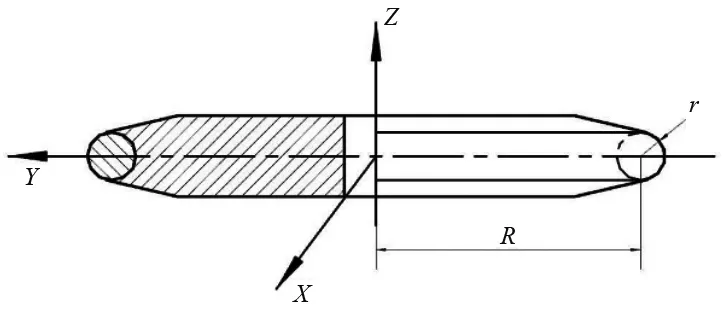
图2 盘铣刀简化模型
则切削刃圆环面在刀具坐标系下的方程为:
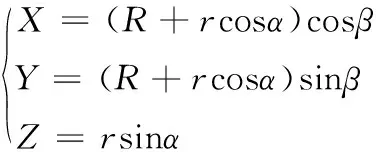
(1)
其中,r为刀尖圆弧半径;R为旋转轨迹圆半径;α为切削接触点所在圆母线与XOZ平面的夹角;β为切削接触点所在圆母线与X轴的夹角。
在VERICUT刀具管理器中增加铣刀模型,使用“旋转面轮廓”命令创建刀盘和刀柄模型,并根据实际尺寸设置装夹方向、装夹点和对刀点,如图3所示。

图3 刀具刀柄模型
1.3 附属模型
以新不对称型线中的日立型线为例[7],其阴转子端面型线如图4所示。
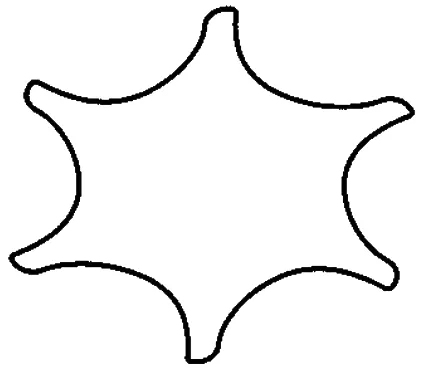
图4 阴转子端面型线
设阴转子端面型线的参数方程为:

(2)
转子的端面型线绕中心轴作螺旋运动,当端面型线相对于其原始位置转过τ角时,轴线前进距离为z。则阴转子左旋螺旋面的参数方程为:

(3)
其中,P(τ)表示阴转子变螺距圆柱螺旋线的轴向参数方程。
式(3)亦可以用矢量式表示:
s=s(θ,τ)=[x0(θ)cosτ+y0(θ)sinτ]i+
[-x0(θ)sinτ+y0(θ)cosτ]j+[P(τ)]k
(4)
设θ为常数而改变τ时,得到的τ参数方程就表示以初始端面型线上不同点为起点的一条条螺旋线;设τ为常数而改变θ时,得到的θ参数方程就表示在不同位置的端面型线。
设其变螺距圆柱螺旋线的方程为:
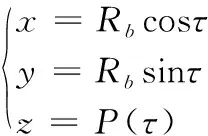
(5)
其中,Rb为以端面型线上不同位置点为起点的螺旋线的基圆半径。
根据端面型线和变螺距圆柱螺旋线的参数方程使用Solidworks软件中“方程式驱动的曲线”命令绘制出型线和螺旋线,再使用“扫描”命令可以得到变螺距螺杆的三维模型。
在5轴联动数控加工螺杆时,为了保证加工精度,必须保证螺杆毛坯在机床工作台上正确定位。螺杆的中心轴是其设计基准,为了避免基准不重合产生的定位误差,故选用中心轴线为定位基准。
在项目树C轴“Attach(附属)”下添加“Fixture(夹具)”和“Stock(毛坯)”,如图5所示。
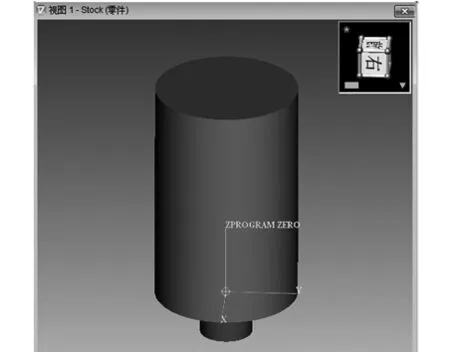
(a) 毛坯及夹具
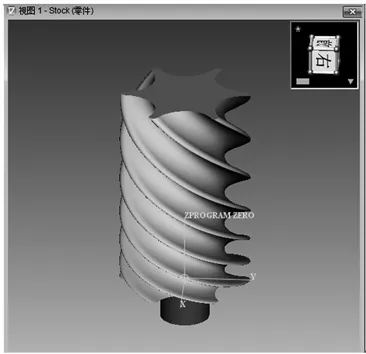
(b) 螺杆精确模型及夹具 图5 附属模型
2 数控加工程序的编制
2.1 螺旋曲面的插补算法
螺旋曲面是有规律的规则曲面,采用参数线法将曲面划分为θ和τ两个方向的加工,并使用时间分割法求解接触线上各插补点的坐标位置。
为了使数控加工朝着高速、高精度的方向发展,保证加工过程的安全,刀具在进行变螺距螺杆螺旋曲面的加工时,其空间加工轨迹必须满足以下几个控制条件:
(1)进给步长必须在给定的最大进给步长的范围内;
(2)插补轨迹的轮廓弓高误差必须在给定范围内;
(3)加工的法向加速度必须在给定范围内。
使用时间分割法被微小直线段分割的变螺距螺旋线可近似为圆弧,根据微分几何关系,插补的弓高误差δh与插补步长L1以及轮廓曲线的曲率半径ρ之间存在如下关系:
(6)
给定允许的最大轮廓误差δhmax并代入式(6)中可以计算出对应的插补步长:
(7)
由于曲率半径ρ的计算较为复杂,联立式(6)和式(7)便可在避免求ρ的情况下得到最大轮廓误差下的插补步长:
(8)
当加工到某一插补点,进给速度不变时,进给的最大法向加速度amax以及轮廓曲线上该点的曲率ρ之间存在如下关系:
(9)
同样,为了避免计算曲率半径ρ,联立式(7)和式(9)可以得到在给定的最大法向加速度amax下的插补步长:
(10)
根据以上3个控制条件计算出来的3个进给步长分别为L1、L2、L3,取
L=min{L1,L2,L3}
(11)
其中,L1=FT为只考虑进给速度的无约束进给步长。求得的L即为同时满足无约束进给步长,弓高误差以及进给加速度约束条件的期望进给步长。
设螺旋线的参数方程为l(τ)=(x(τ),y(τ),z(τ)),进给速度为v(t),插补周期为T,由微分几何关系可得:
(12)
其中,
(13)
联立式(12)和式(13)有:
(14)
则旋转角τ的增量:
(15)
第i+1个插补点的旋转角为:
τi+1=τi+△τ
(16)
取τ0=0,根据△τ可以求解出该螺旋线上所有插补点的位置。同样,使用参数线法规划走刀路径,可以求解出一个螺旋曲面上所有插补点的位置。
2.2 刀位点的求解
根据插补算法求得的插补点就是加工时刀具和螺旋曲面的接触点,如图6所示是加工时刀具与工件啮合的示意图。xoy为工件坐标系,XOY为刀具坐标系。工件坐标系下,设某一加工时刻的接触点为M(x,y,z),刀尖圆弧中心点为N(xN,yN,zN),刀具中心点为O(xT,yT,zT),求得刀具中心点O就获得了设计数控程序所需要的全部信息。
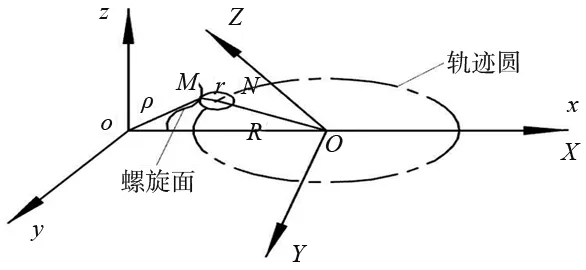
图6 刀具与螺旋面啮合示意图
设螺旋曲面上任一点的法矢量为n,则有:
(17)
式中,
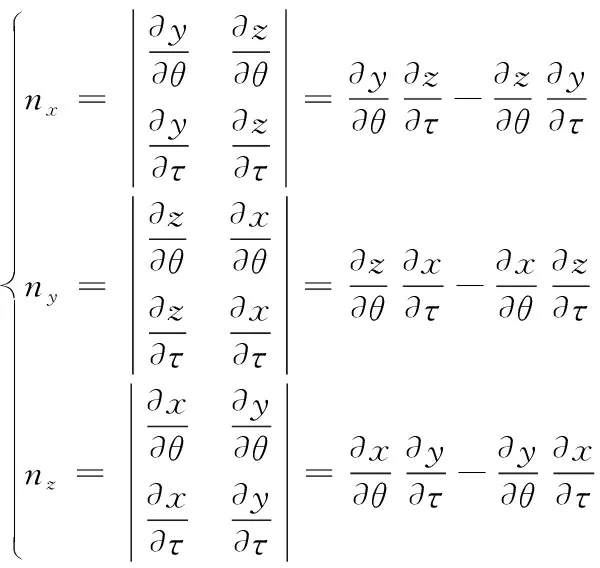
(18)
由空间啮合原理可知,在任一加工时刻,螺旋曲面上接触点M处的法矢量经过刀尖圆弧中心点N,故有:
oN=oM+MN
(19)
其中,
oM=xi+yj+zk=ρ
(20)
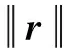
MN=r=re=rxi+ryj+rzk
(21)
其中,
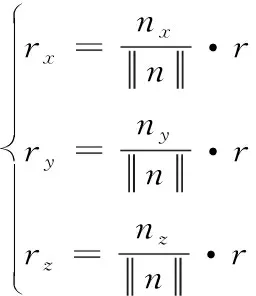
(22)
(23)
故有:
oN=xNi+yNj+zNk=ρ+re
(24)
求得刀尖圆弧中心点N的坐标为:

(25)
为了降低变螺距螺杆加工对机床的要求,利用螺杆加工时绕自身轴线的旋转运动,取插补点运动到xoz平面时为实际加工接触点,则刀具中心点O的坐标为:

(26)
3 数控加工仿真的实现
3.1 碰撞检查和行程极限配置
碰撞检查功能主要是为了检查主轴、刀具、刀柄和毛坯在加工过程是否发生碰撞,提高加工过程的安全性,忽略切刀和毛坯的碰撞。
行程极限设置是根据机床实际的行程范围,对其线性轴和旋转轴的运动进行限制,可以判断机床在加工过程中是否超程,同时也验证了工件装夹定位的合理性[8]。其中,C轴为螺杆旋转的中心轴,其行程范围为0°~360°,可忽略C轴的超程检查。
3.2 坐标系统配置
在项目中添加新的坐标系,并附上坐标系到“Stock(毛坯)”,将该坐标系重命名为“PROGRAM ZERO(程序零点坐标系)”,该坐标系原点必须与实际编程时的程序零点重合。
3.3 G代码偏置
本文的五轴加工程序只涉及一个编程坐标系,故偏置名选择“程序零点”,“寄存器”中输入1;主轴上有旋转轴,故在“从”/“到”定位选择从“组件”“Spindle(主轴)”到“坐标原点”“PROGRAM ZERO(程序零点坐标系)”定位[9]。
在项目树选项卡窗口的相关相关参数设置完成之后[10],将机床“Base(床身)”隐藏,某一时刻的仿真双视图如图7所示。

图7 加工仿真窗口
4 结束语
研究了空间螺旋线的直接插补算法和刀具刀位点的求解过程,编程得到了变螺距螺杆的5轴数控加工程序;通过DMU80T的5轴机床模型、附属模型和刀具刀柄模型的建立,定制变螺距螺杆在VERICUT的加工仿真环境,实现了变螺距螺杆的多轴数控加工仿真。
该仿真可以代替零件在实际加工中的试切过程,提高螺杆加工的效率和安全性,为变螺距螺杆的多轴数控加工提供了参考。

