覆冰四分裂导线的气动特性和舞动特性分析

向 玲,张 悦,唐 亮

(华北电力大学 机械工程系,河北 保定 071003)

导线覆冰后截面形状改变,在风载荷的作用下会诱发一种低频率(约为0.1～3 Hz)、大振幅(约为导线直径的5～300倍)的自激振动,即舞动,造成线路金具损坏、断线、杆塔损坏等事故[1].风吹过覆冰导线产生的升力、阻力及扭矩为诱发舞动的重要因素.因此,覆冰导线气动力参数的获取和舞动特性分析对线路防舞研究具有重要意义.

通常是通过风洞试验获得覆冰导线的气动力参数.Oka等[2]进行了新月形覆冰气动力特性试验,研究了覆冰截面的气动力特性.顾明等[3]计算了典型覆冰单导线的气动力参数.李万平等[4-5]进行了覆冰三分裂导线的静态和动态气动力特性测试并对比分析.张宏雁等[6]通过风洞试验获得覆冰四分裂导线的气动力参数.风洞试验虽然能够准确地测得导线的气动力参数,但是存在成本高、周期长等缺点.随着计算流体动力学 (Computational Fluid Dynamics,CFD)技术的快速发展,研究发现利用数值模拟获得的气动力参数可以准确地反映覆冰导线的气动力系数随攻角的变化规律.姚育成等[7]建立了单导线扰流的数值模型,对扰流场的流动结构及气动力特性进行了研究.陈元坤等[8-9]模拟了分裂导线的扰流问题,分析了各子导线相对位置对气动力参数的影响.

在舞动数值模拟研究方面,Desai等[10]较早采用有限元法模拟了覆冰单导线的舞动.李黎等[11]将分裂导线等效为单导线进行舞动的模拟,研究了风速和初始攻角对舞动的影响.刘海英等[12]建立了覆冰四分裂模型中覆冰导线的面内和扭转两个方向的非线性动力学方程,讨论了初始风攻角和面内结构阻尼对系统稳定性及舞动幅值的影响.刘小会等[13]建立了覆冰四分裂非线性有限元方程并编写了计算程序,模拟了不同档距四分裂线路的舞动.

典型的覆冰导线截面形状有扇形、D形和新月形.本文首先用Gambit软件建立了新月形覆冰四分裂导线的数值模型;然后运用Fluent软件模拟了其在风载荷作用下导线的扰流流场,计算得到各子导线的气动力系数随风攻角的变化规律;最后建立单档四分裂线路的有限元模型,将整体气动力系数加载到有限元模型进行线路整体舞动的模拟,通过舞动位移响应、舞动轨迹及位移频谱对不同初始风攻角的舞动特性进行分析.本文所得结论对覆冰四分裂导线防舞技术的研究有重要意义.

1 覆冰导线数值模型的建立

以新月形覆冰四分裂导线为研究对象,导线覆冰初凝角为0°,导线直径D为26.82 mm,覆冰厚度为12 mm,子导线间距s为450 mm,建立新月形覆冰四分裂导线模型及各子导线编号如图1所示.架空输电导线属于典型的细长结构,其气动力特性主要由截面形状决定.因此,可以将覆冰导线简化为二维结构来研究其在风场中的扰流问题[14].

为保证不同攻角下的模型充分流动,建立大小为2 m×2 m的流场区域,导线处于流场区域中心.网格划分质量的好坏直接影响计算结果的准确性.

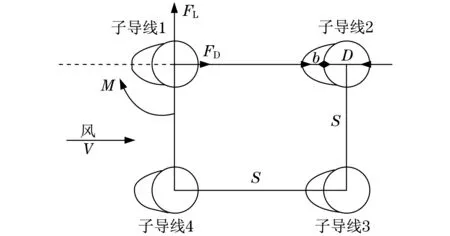
图1 导线模型Fig.1 Model of bundle conductor

结构化网格和非结构化网格各有优缺点.非结构化网格有较好的自适应性,综合考虑,运用Gambit软件对流场区域进行非结构化网格划分,并在导线附近进行网格加密.划分之后网格总数为19.5万,划分结果及导线周围的网格局部放大如图2(b)所示.

图2 网格划分Fig.2 Mesh of the numerical model

利用Fluent模拟导线的扰流流场时采用SIMPLE算法,湍流模型为Spalart-Allmaras模型,采用三阶迎风格式进行网格离散,时间步长为0.001 s,时间步数为200,计算时选择分析类型为瞬态分析[14].风攻角α的变化范围为0°～180°,每隔10°进行一次导线扰流场的模拟.模拟不同迎风攻角下导线扰流场,保持导线模型及网格不变,只改变来流方向和边界条件,来流方向按逆时针方向变化.具体边界条件设置如下:当攻角为0°时,左边界为速度入口,右边界为自由流动出口,该边界条件适用于出口的速度和压力为未知的情况,上下边界和导线设置为壁面;当攻角为10°～80°时,左边界和下边界为速度入口,右边界和上边界为自由流动出口,导线设置为壁面;其余攻角下的边界条件设置同理.

2 覆冰导线气动力特性数值模拟

2.1 导线尾流效应分析

风吹过覆冰导线时,导线附近会周期性地脱落旋转方向相反的漩涡.图3为风速12 m/s、冰厚12 mm时的4个典型风攻角下导线扰流场的速度云图.从图3中可以看出:当风攻角α=0°时,子导线2,3处于子导线1,4的尾流中,受到子导线1,4尾流的影响,使得子导线2,3周围的风速不同于子导线1,4周围的风速;当风攻角α=45°时,子导线2受子导线4尾流的影响;当风攻角α=90°时,子导线1,2分别受到子导线3,4尾流的影响,此时导线迎风面积达到最大,导线的尾流效应也达到最大;当风攻角α=135°时,子导线1受到子导线3尾流的影响.从图3可以得出,迎风侧子导线对背风侧的导线起到了遮挡作用,导致背风侧子导线气动力系数有一定的变化.

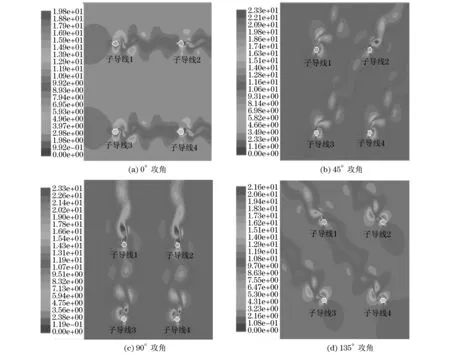
图3 典型攻角下的速度云图Fig.3 Velocity contours of iced bundle conductor at typical attack angles

2.2 气动力系数随攻角的变化规律

导线在风载荷的作用下产生升力FL、阻力FD及扭矩FM,对应的无量纲系数计算公式为

(1)

式中:CL,CD,CM分别为升力系数、阻力系数和扭矩系数;ρ为流体密度,此处取1.225 kg/m3;D为导线直径26.82 mm;V为风速,m/s.

新月形覆冰四分裂导线在风速为12 m/s、覆冰厚度为12 mm时的气动力系数随攻角的变化规律如图4所示.

经与文献[9]中风洞试验结果对比,模拟所到的气动力系数随攻角的变化规律与文献中的相同.

当迎风攻角α=0°时,导线迎风面积最小,阻力系数最小,此时子导线2,3分别受子导线1,4尾流的影响,阻力系数小于子导线1,4;当α=45°时,子导线2处于子导线4的尾流区,受到子导线4尾流的影响,阻力系数降低;当α=90°时,覆冰导线迎风面积达到最大,同时尾流效应也达到最大,处于尾流区的子导线1,2阻力系数大幅下降;同理,当α=135°和α=180°时,处于尾流区的子导线阻力系数有所下降.

各子导线的升力系数随攻角改变的变化曲线整体呈波状.当α=0°,α=90°,α=180°时,各子导线升力系数为0.当α=45°时,子导线2受子导线4尾流的影响,升力系数有所增加;在其余攻角处,升力系数不受尾流效应的影响,各子导线的升力系数相同.各子导线扭矩系数在攻角α为0°,140°及180°时等于0,扭矩系数基本不受尾流的影响,各子导线的扭矩系数随攻角的变化规律相同.

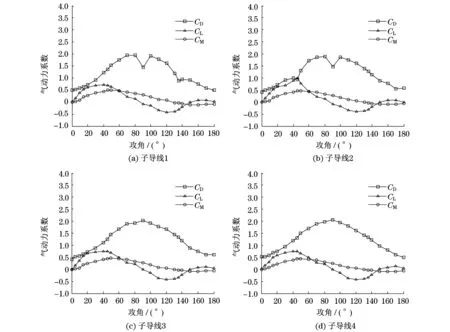
图4 新月形覆冰四分裂导线的气动力系数Fig.4 Aerodynamic coefficient of crescent iced quad bundle conductor

3 覆冰四分裂导线舞动特性分析

3.1 覆冰四分裂导线有限元模型的建立

使用ANSYS有限元软件建立超高压输电四分裂线路的有限元模型,导线采用索单元模拟,梁单元模拟子间隔棒,档距为240 m,四分裂导线直径、子导线间距与上文数值模型一致,其他物理参数参考文献[15],建立如图5所示的导线有限元模型.

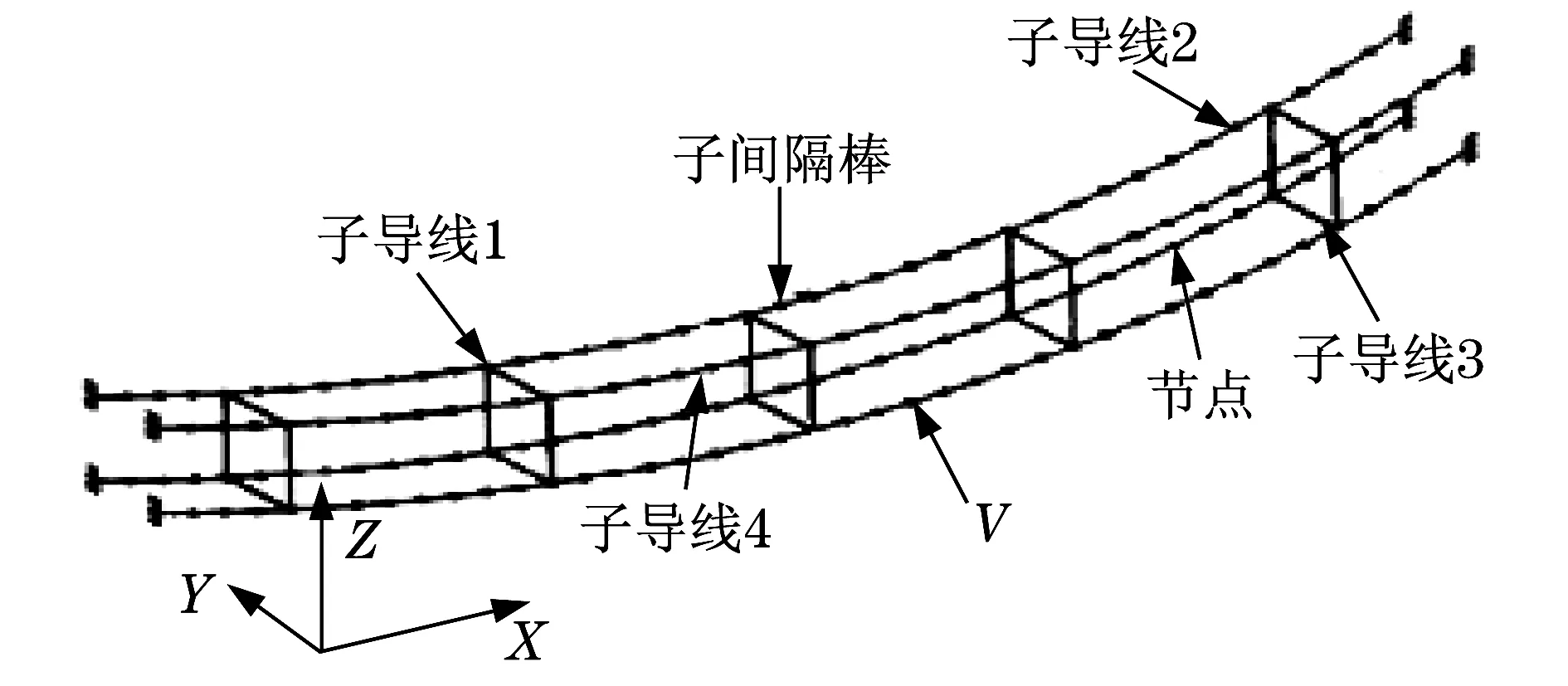
图5 四分裂导线有限元模型Fig.5 Finite element model of bundle conductor

为分析四分裂导线的舞动特性,首先进行其动力特性的分析,计算得到四分裂导线的前三阶振型及固有频率,如表1所示.

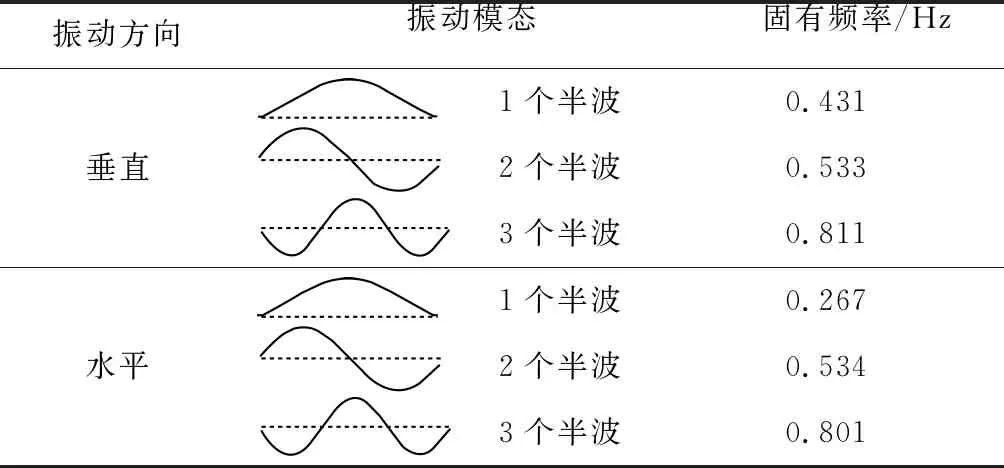
表1 覆冰四分裂导线的模态特征Tab.1 The iced quad bundle conductor’s modal characteristics

3.2 覆冰导线的气动激励

在模拟舞动的过程中,覆冰导线所受到的载荷包括静载荷和动载荷两部分,重力载荷为静载荷,动载荷主要是气动力载荷,如图6所示.

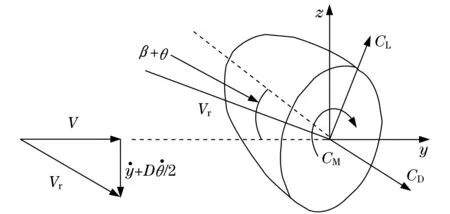
图6 覆冰导线截面的气动力及风攻角示意图Fig.6 Attack angle and aerodynamic forces of conductor section

作用在覆冰导线截面上的气动力载荷表示为[15]

(2)

式中:Fy,Fz分别为y向和z向的节点气动力载荷.

t时刻α的计算公式为

(5)

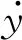
从式(5)可以看出,t时刻的风攻角不仅与初始风攻角有关,而且还会受到垂直方向和扭转运动的影响.

受子间隔棒约束作用的影响,分裂导线舞动时表现为显著的整体运动[15],因此,为探究子间隔棒的具体约束作用进行了四分裂线路整体舞动的模拟.通常是用单导线的气动力系数代替分裂导线的整体气动力系数,从上文得知,由于尾流效应的影响,单导线气动力系数随风攻角的变化规律并不能准确反映分裂导线整体气动力系数随风攻角的变化规律.分裂导线的整体升力系数和整体阻力系数的定义如下[16]:

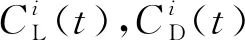
分裂导线的整体扭矩系数定义为

(8)

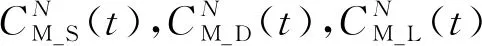
对于四分裂导线,可以表示为

(9)

模拟所得各子导线的气动力系数,覆冰四分裂导线的整体气动力系数随攻角的变化规律如图7所示.将整体气动力系数加载到四分裂线路有限元模型,进行线路整体舞动的模拟,风速为12 m/s.

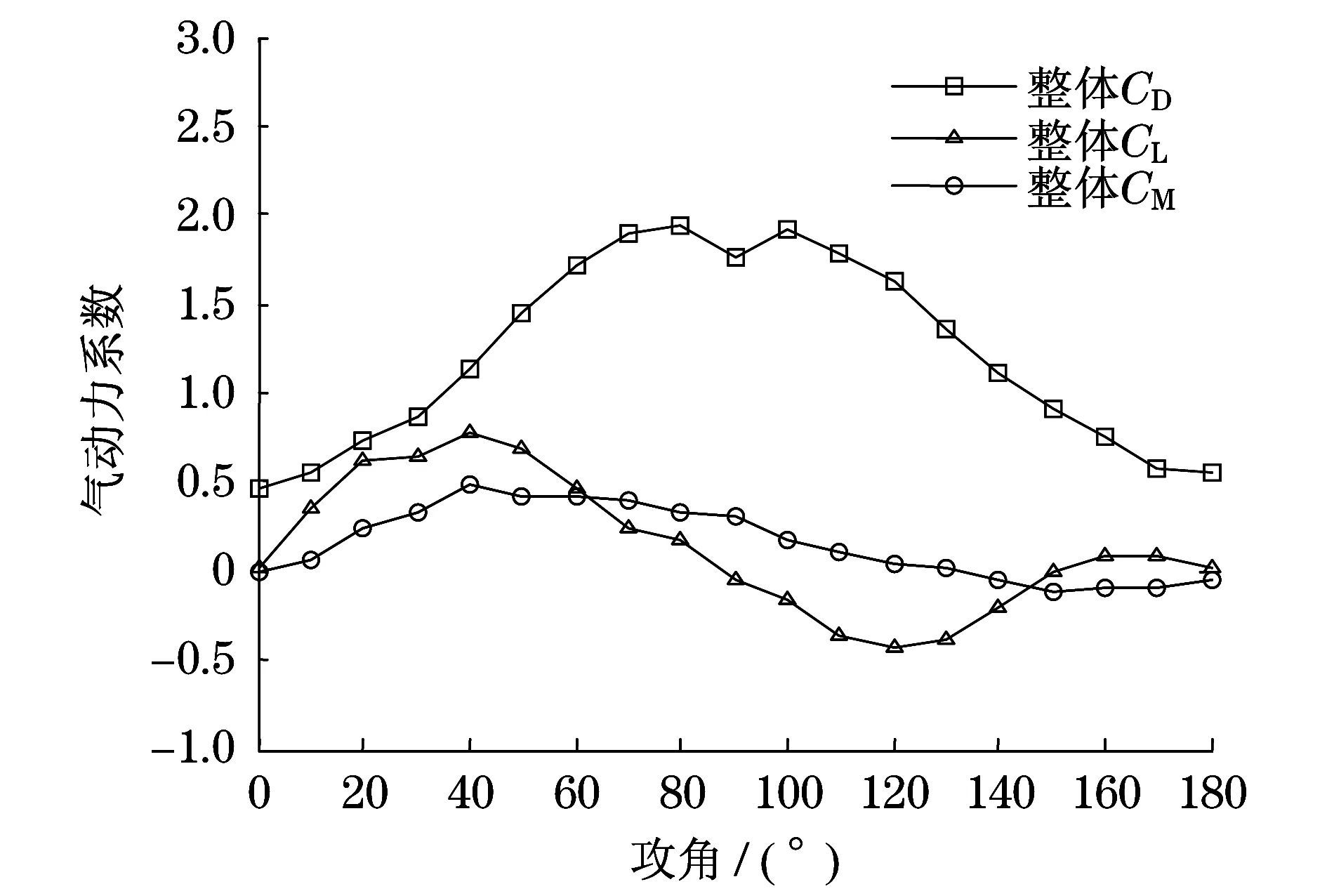
图7 新月形覆冰四分裂导线整体气动力系数Fig.7 The overall aerodynamic coefficient of crescent iced quad bundle conductor

此次舞动模拟是基于Den Hartog垂直舞动机理,当升力系数斜率为负时,覆冰导线可能发生垂直舞动.从图7中可得：覆冰四分裂线路在初始风攻角为40°～110°及170°～180°时可能发生舞动.

3.3 初始攻角不同时的舞动特性分析

经选取不同初始风攻角模拟验证,四分裂线路在初始风攻角为70°和100°时发生大幅舞动,其余初始风攻角未见舞动发生.图8和图9分别为不同初始风攻角70°和100°下线路档距中点的舞动位移时程图、舞动轨迹.

从图8(c)和图9(c)可以看出：舞动以垂直方向为主,轨迹近似呈椭圆形.这与目前舞动研究领域普遍认同的舞动机理所描述的舞动形态是吻合的,即舞动是一个逐渐形成的过程,初期导线在平衡位置附近呈小振幅的摆动,由于风能的积累和空气负阻尼的作用,水平振幅逐渐减小,同时垂直振幅增大,形成不断变大的椭圆形舞动轨迹,最终受系统阻尼影响而逐渐趋于稳定.这也从侧面证明了模拟的正确性.

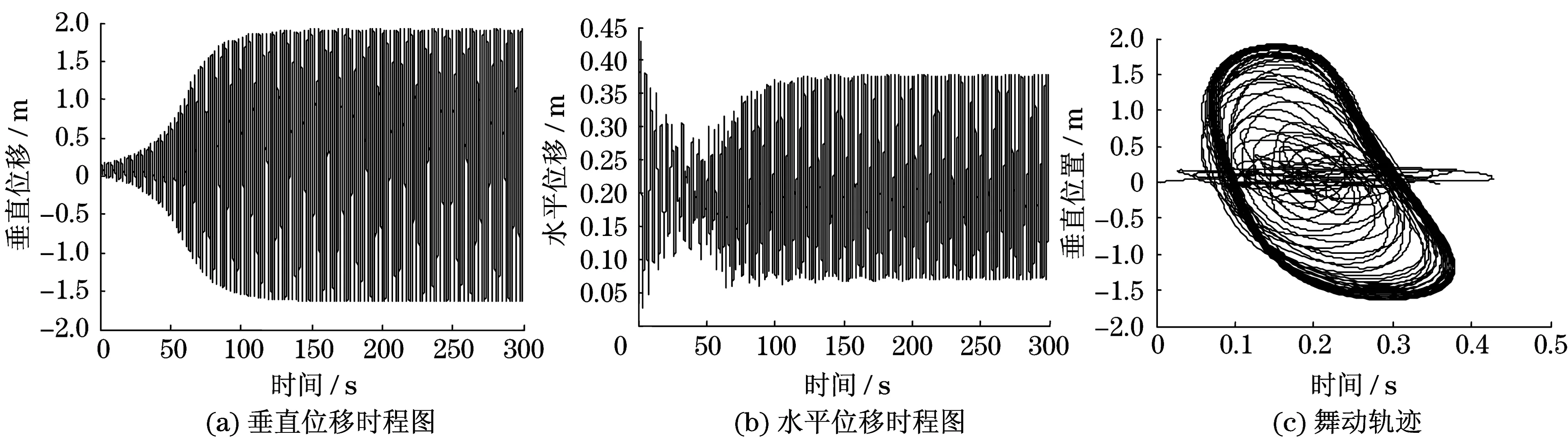
图8 初始风攻角70°下的舞动位移时程Fig.8 Time histories of displacements of initial wind attack angle of 70°

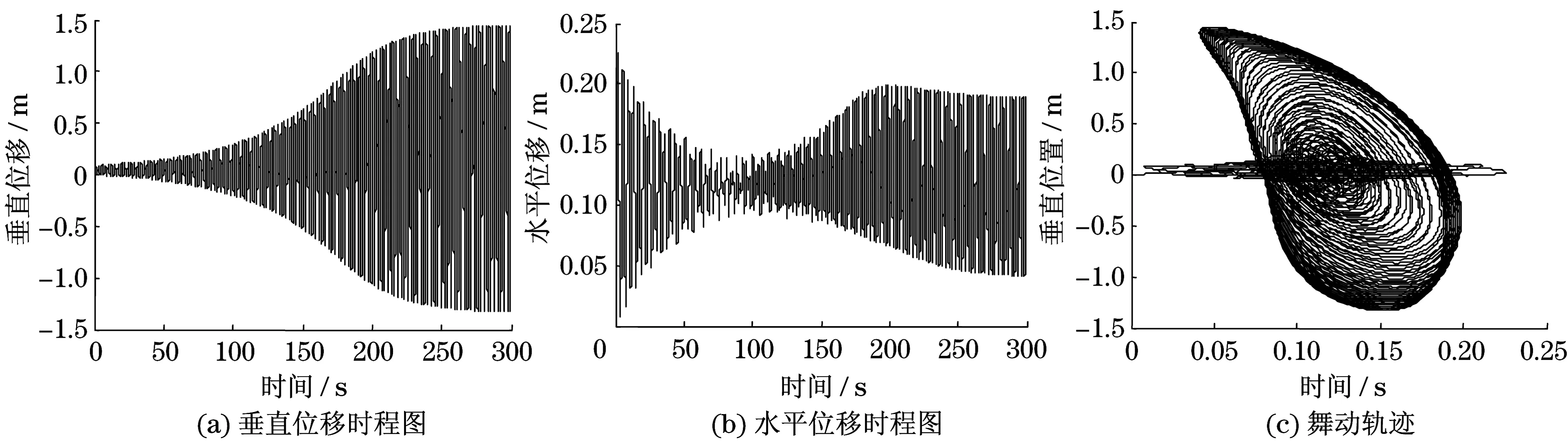
图9 初始风攻角100°下的舞动位移时程Fig.9 Time histories of displacements of initial wind attack angle of 100°

进一步通过位移频谱分析四分裂线路的舞动特征.图10和图11为不同初始风攻角下舞动的位移频谱图.在垂直和水平位移频谱中,接近垂直方向的1个半波固有频率0.431 Hz处有明显的峰值,表明不同初始风攻角下的舞动模式均为垂直方向1个半波舞动.

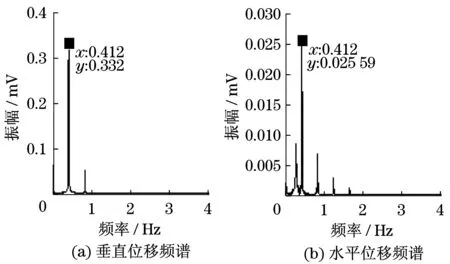
图10 初始风攻角70°位移频谱Fig.10 The displacement spectrum of initial wind attack angle 70°

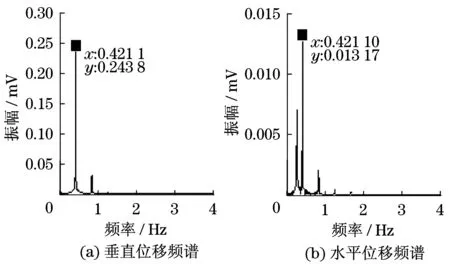
图11 初始风攻角100°位移频谱Fig.11 The displacement spectrum of initial wind attack angle 100°

4 结论

利用Fluent软件模拟得到新月形覆冰四分裂导线的各子导线气动力系数随风攻角的变化规律,建立覆冰四分裂线路的有限元模型,将整体气动力系数加载到有限元模型上进行舞动的模拟.结果表明:尾流效应使得各子导线的气动力系数随风攻角的变化规律不同;覆冰四分裂线路在初始风攻角为70°和100°时发生大幅舞动;在垂直和水平位移频谱中,接近垂直方向的1个半波固有频率处均有明显峰值,初始风攻角不同舞动的幅值及轨迹不同,但舞动模式均为垂直方向的1个半波舞动.