液压球阀磨损可靠性分析

王海芳,褚天争,邱 豪,张伯禄,刘广阔

(1.东北大学秦皇岛分校 控制工程学院,河北 秦皇岛 066004; 2.河北省自动化研究所 先进制造技术研究室,河北 石家庄 050081)

液压阀作为液压系统的控制元件,起到连接能源元件(液压泵)与执行元件(液压缸、马达)的作用.在实际工作中,液压阀阀芯与阀座间的长期往复运动,造成了不可避免的材料磨损.磨损会导致阀芯与阀座表面损坏、液压油外泄流,使液压阀失效,这对其使用寿命会造成严重影响[1].液压阀作为液压系统中的核心元件,为保证液压系统的正常运行,针对其基于磨损的可靠性分析十分必要.

很多学者对机械、液压系统及元件的可靠性做了相关研究.在可靠性计算方面:张义民等[2]采用摄动方法研究了车辆后桥的可靠性灵敏度设计问题;胡登高等[3]应用有限元法对液压支架进行了强度可靠性及敏感性计算;黄伯超等[4]基于性能可靠性约束对智能液压泵进行了节能优化;张天霄[5]基于一次二阶矩的中心点方法对液压锥阀进行了可靠性分析.在可靠性故障分析方面:陈东宁等[6]基于T-S模糊故障树和贝叶斯网络对多态液压系统进行了可靠性分析;徐格宁等[7]基于贝叶斯网络对汽车起重机液压系统进行了可靠性评估;丁飞等[8]对液压支架结构进行了疲劳动态可靠性评估.在可靠性试验方面:郭锐等[9]应用非线性最小二乘法和最优化理论进行液压泵性能参数退化轨迹研究,提出了液压泵可靠性短时试验方法;陈东宁等[10]进行了液压软管总成可靠性试验及评估;张根保等[11]针对液压缸进行了漏油可靠性强化试验加速应力分析.

目前,针对机械零件的可靠性分析往往以零件材料的强度为判断依据,但是在液压元件的实际工作中,此依据并不完全适用.液压元件常常以泄露为主要失效形式,此时材料未发生屈服而只是因为磨损而导致零件机理失效[11-12].根据实际工作经验,液压阀的可靠性与其结构尺寸、工作环境参数有较大的关系,本文基于磨损机理进行磨损深度计算,定义磨损极限多参数状态函数,应用一次二阶矩设计验算点法,基于Matlab求得球阀磨损可靠度,并分析相关参数对磨损可靠度的影响.本工作为液压元件的设计提供理论基础,有利于在设计阶段对其结构尺寸做出一定的优化,也有利于后期元件工作参数的设定优化.

1 球阀的受力分析和磨损深度计算

磨损是机械设备和元件的一种基本失效形式.在磨损情况下,零件尺寸和摩擦表面状态会逐渐改变.Archard提出了简单黏着磨损计算公式并得到广泛应用[13-14].

磨损体积

(1)

式中:VQ为零件磨损体积,m3;K为磨损系数，无量纲参数;N为接触表面的正压力,N;L为材料相对滑移距离,m;σs为材料的压缩屈服强度,MPa.

按照材料定义,软性金属材料的硬度约等于3倍的材料压缩屈服强度,即3σs≈H,则式(1)可改为

(2)

在液压系统工作中,球阀阀芯与阀座间的往复运动造成材料磨损，导致阀芯与阀座表面损坏,液压阀失效.图1为球阀阀芯的受力分析示意图.

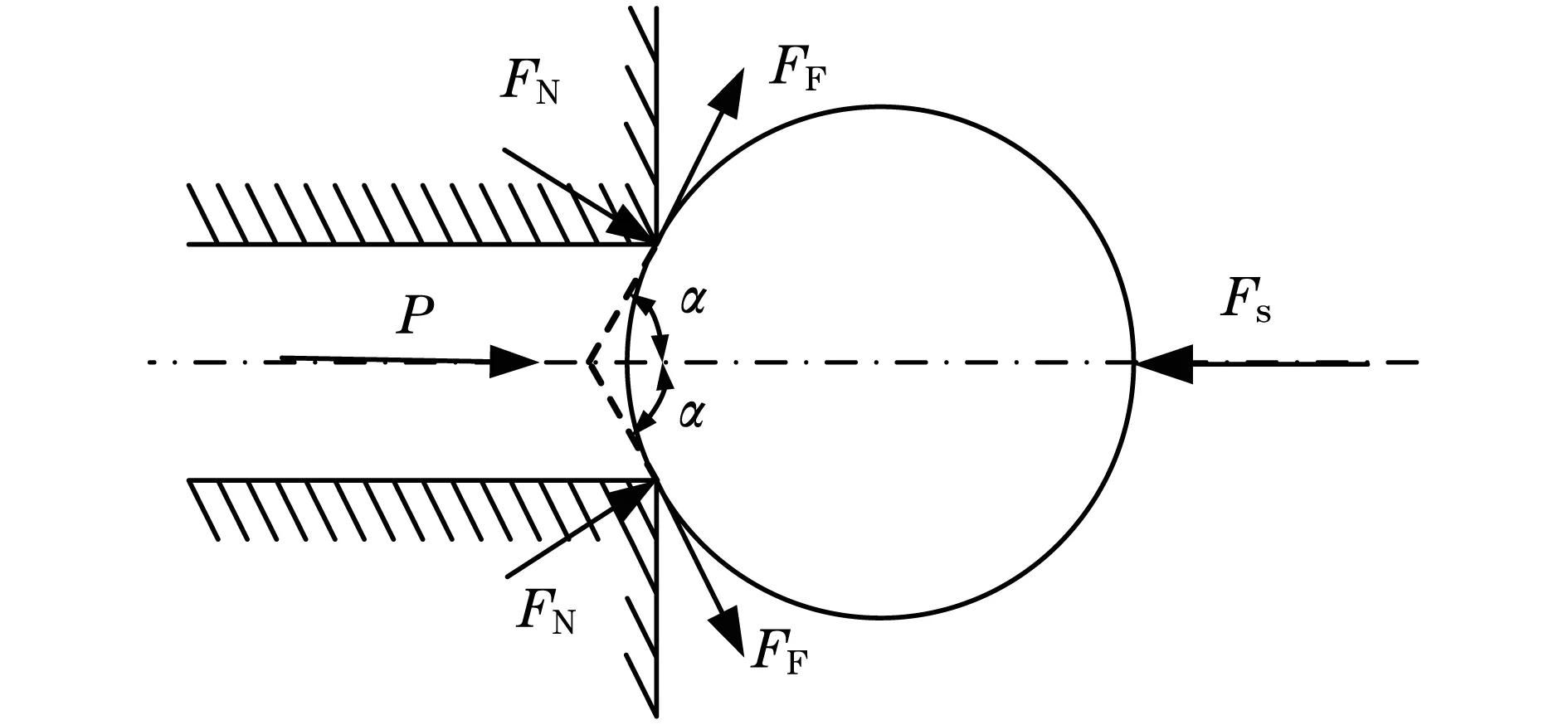
图1 液压球阀阀芯的受力示意图Fig.1 Stress of the hydraulic ball valve spool

阀芯与阀座在平均直径为d的圆周上接触,接触周长S=πd,接触面积A=πd2/4,阀座对阀芯会产生垂直于接触表面并指向阀芯的正压力FN,还会产生沿着阀芯表面的摩擦力FF,以Fs表示弹簧预紧力,PA表示液压产生的管内正压力,若管内压力小于弹簧预紧力,即PA≤Fs,阀关闭,阀芯与阀座接触.阀芯的受力满足平衡方程,可以表示为[5,15]

(3)

则垂直于球阀阀芯接触表面并指向阀芯正压力的合力N可以表示为

(4)

图2为球阀阀芯与阀座接触之后发生磨损的示意图.

图2 液压球阀阀芯磨损示意图Fig.2 Abrasion of the hydraulic ball valve spool

由图2知,α=arccos(d/2R),h=h1cosα,经推导磨损环状球台体的体积VQ可表示为

(5)

由图2的几何关系得

(6)

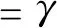
(7)

液压阀在使用中反复开闭,磨损是一个非线性的过程,但为了计算方便,本文仅以线性方程代替,设闭合n次,则球阀的磨损深度为

(8)

2 一次二阶矩设计验算点法

一次二阶矩中心点法将非线性极限状态方程在中心点处泰勒展开,当方程的非线性程度较高时,将其线性泰勒展开会带来较大误差[16].设计验算点法将功能函数的线性化Taylor展开点选在失效面上,从而解决了中心点法存在的问题,又称为改进一次二阶矩法.

设零件的极限状态方程为

(9)

(10)

在点x*处按Taylor级数展开并取至一次项,有

(11)

(12)

零件结构的可靠性指标为

(15)

将式(11)对应的极限状态方程ZL=0做变换Xi=σXiYi+μXi,Yi是标准正态随机变量,应用式(14)和式(15),切超平面方程ZL/σZL=0可写成

(16)

定义Xi的灵敏度系数为

(17)

灵敏度系数反映了线性函数ZL与变量Xi之间的线性相关性,则式(17)可表示为

(18)

式(18)表示在标准正态随机变量Y空间的法线式超平面方程,法线就是极限状态平面上的点p*(在X空间中的坐标为x*)到标准化空间中原点O(在X空间中的坐标为μX)的连线,其方向余弦为αYi=cosθYi,长度为β.这样,可靠性指标β就是标准化正态空间中坐标原点到极限状态面的最短距离,与此相对应的极限状态面上的点p*就称为设计验算点,常简称为验算点或设计点.图3为二维情况下的可靠性指标和设计点的几何意义.

设计验算点p*在标准化正态变量Y空间中的坐标为

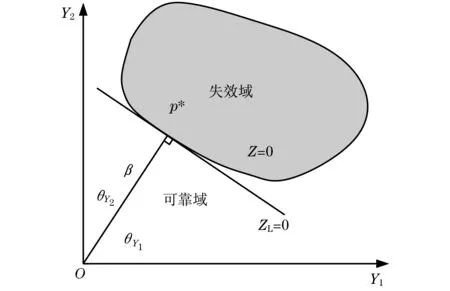
图3 标准正态随机平面上的可靠性指标和设计验算点

(19)

在原始X空间中的坐标为

(20)

利用上述可靠性指标的几何意义,可靠性指标的求解归结为约束优化问题，即

(21)

基于设计点法的迭代具体步骤为:取初始值x*=μX,依据式(17)求解αXi,依据式(15)计算β,应用式(20)计算新的x*,以此迭代满足精度要求,即求得最终的β和x*.

3 液压球阀的可靠度计算和分析

基于上述液压球阀的受力分析和磨损深度计算公式,建立球阀磨损极限状态函数,结合一次二阶矩设计验算点法,利用Matlab软件求得液压球阀的磨损可靠度和设计验算点;然后分析球阀结构尺寸和工作环境参数对可靠度的影响,又与蒙特卡洛仿真值比较验证计算值,为球阀设计和使用提供理论基础.

3.1 球阀可靠性分析

基于式(8)和式(9)建立球阀的磨损极限状态函数为

(22)

式中:hmax为球阀磨损深度的允许最大值.

选取基本随机参数向量X=[dPFsfHK]T,均服从正态分布,摩擦系数f和磨损系数K为相关随机参数变量,其相关系数为ρfK,则定义其均值向量μX为

(23)

协方差矩阵CX为

(24)

根据式(12),gX(x*)的梯度为

(25)

确定初始设计点x*,应用式(10)、式(15)、式(17)和式(20),迭代运算,计算出基于设计验算点法的球阀磨损可靠度指标和设计验算点,下面通过具体的算例进行仿真验证.

3.2 球阀数值算例

以球阀为例,各参数变量服从正态分布,选取球阀磨损深度阈值hmax=0.06 mm,阀座的管道内径d=(6.3,0.397) mm,压力P=(7.5,0.563) MPa,弹簧的预紧力Fs=(200,16) N,摩擦系数f=(0.25,0.015),材料硬度为H=(800,64) N/mm2,磨损系数K=(1.15×10-4,4.285×10-6),磨损系数K和摩擦系数f是相关随机变量,取相关系数为ρfK=0.6,球阀闭合次数取为n=100 000次,球阀半径R=7.0 mm.

确定初始设计点为x*=[6.3 7.5 1750.25 800 1.15×10-4],应用式(10)、式(15)、式(17)和式(20),迭代运算,求得球阀的磨损可靠度指标和设计点为

查表可靠度为

由计算结果可见,各参数变量服从正态分布时,球阀的可靠度很高,能够满足阀使用的标准要求[18].

上述算例计算得灵敏度系数为

选取阀座管道内径d、压力P、弹簧的预紧力Fs、材料硬度H这4个参数说明对可靠度的影响,因摩擦系数f和磨损系数K不易测量标定不作分析.

选取管道直径d=5～7 mm,变异系数Vd=0.1,其余参数同设计验算点法,并且为了验证本文方法的准确性,同时利用蒙特卡洛法进行可靠度仿真[16,19],得到管道内径d与可靠度R的关系曲线(见图4).图4中数据表明:设计验算点法计算值与蒙特卡洛法仿真值接近,设计点法计算值可信,管道直径和可靠度不是单调线性关系,管道直径在d=5.4～6.4 mm范围内,可靠度较高,余下数据可靠度有一定下降.

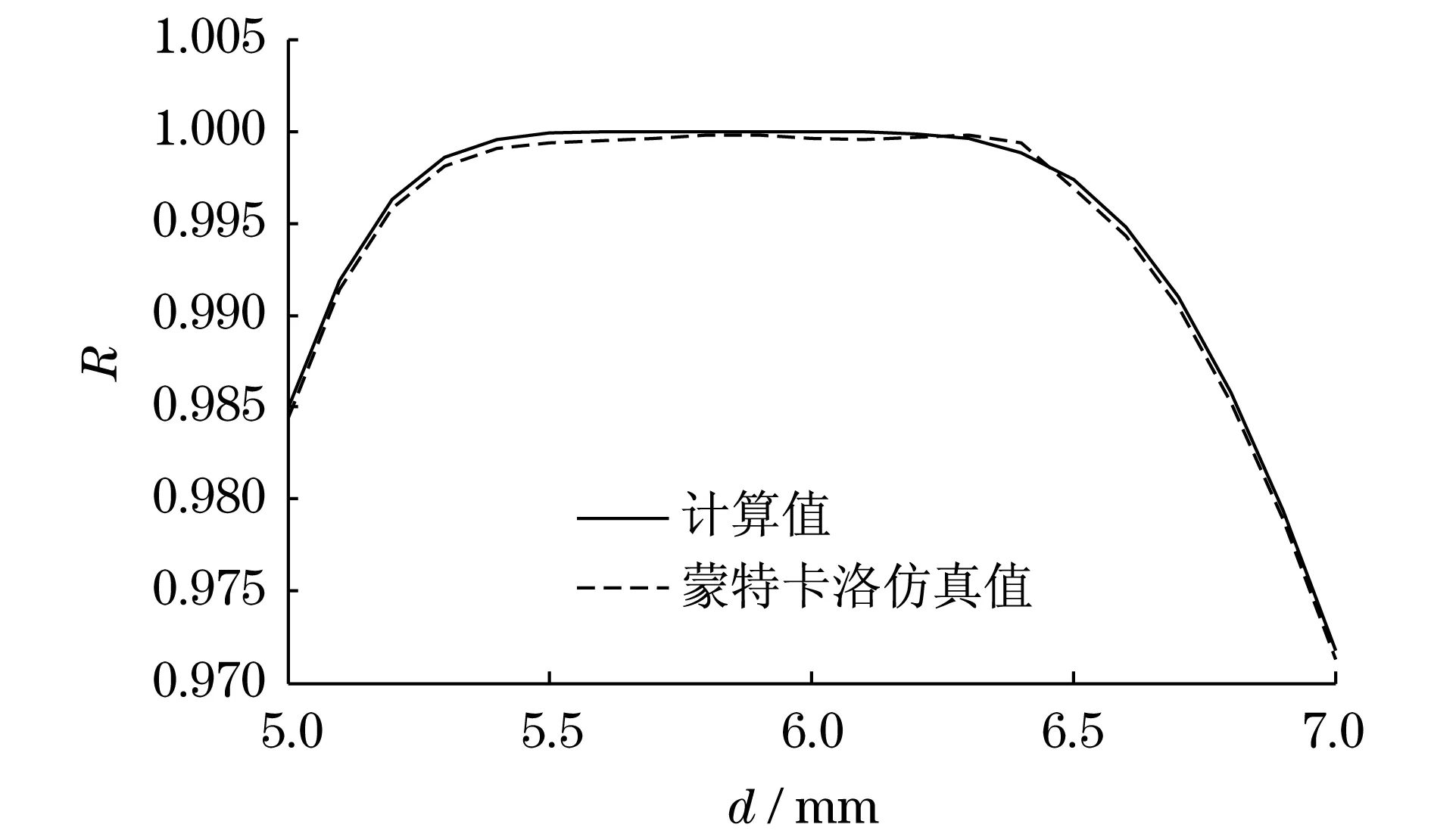
图4 管道直径与可靠度关系曲线Fig.4 Relation curve of pipe diameter and reliability

选取球阀的弹簧预紧力Fs=100～250 N,变异系数VFs=0.02,其余参数同设计验算点法可靠度计算,也进行了蒙特卡洛可靠度仿真,得到弹簧预紧力Fs与可靠度R的关系曲线(见图5).图5中数据表明:设计验算点法计算值与蒙特卡洛法仿真值接近,设计验算点法计算值可信,弹簧预紧力F和可靠度R为单调上升关系,弹簧预紧力F≥180 N,可靠度较高.

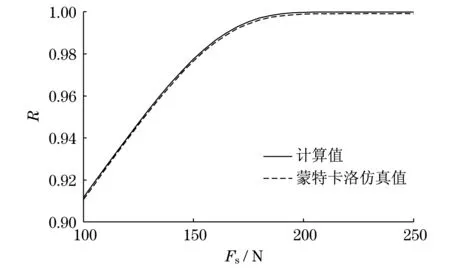
图5 弹簧预紧力与可靠度关系曲线Fig.5 Relation curve of spring preload and reliability

选取压力P=3～10 MPa,变异系数VFs=0.05,其余参数同设计验算点法可靠度计算,也进行了蒙特卡洛可靠度仿真,得到压力P与可靠度R的关系曲线(见图6).图6中数据表明:设计验算点法计算值与蒙特卡洛法仿真值接近,设计点法计算值可信,压力P和可靠度R不是单调线性关系,压力P=5.3～7.7 MPa范围内,可靠度较高.

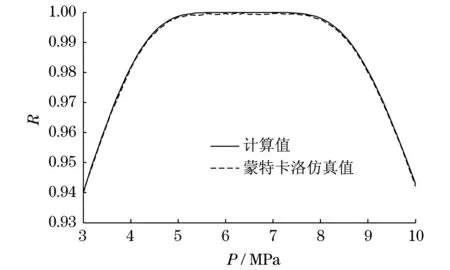
图6 压力与可靠度关系曲线Fig.6 Relation curve of pressure and reliability

选取材料硬度H=700～1 000 MPa,变异系数VFs=0.001,其余参数同设计验算点法可靠度计算,也进行了蒙特卡洛可靠度仿真,得到材料硬度H与可靠度R的关系曲线(见图7).图7中数据表明:设计验算点法计算值与蒙特卡洛法仿真值接近,设计点法计算值可信,材料硬度H和可靠度R为单调上升关系,硬度越大,可靠度值越大.

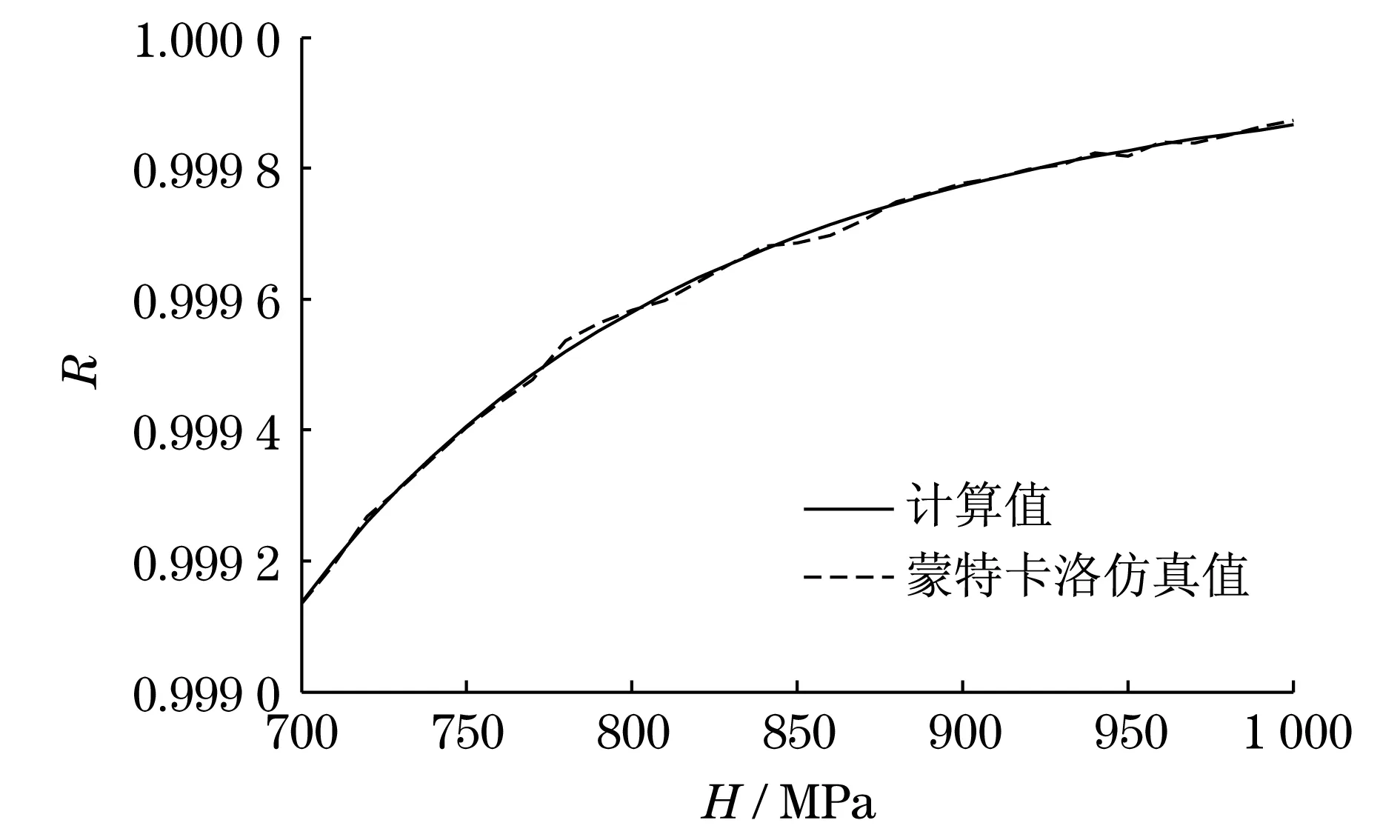
图7 材料硬度与可靠度关系曲线Fig.7 Relation curve of material hardness and reliability

4 结论

对球阀进行了受力分析,用Archard磨损公式建立了球阀磨损线性函数,进而建立球阀磨损极限函数,基于一次二阶矩设计验算点法,求得球阀的磨损可靠度指标和设计验算点,并分析了球阀结构和工作参数对可靠度影响,与蒙特卡洛仿真进行了比较,得出以下结论:

(1) 由一次二阶矩验算点法计算值和蒙特卡洛仿真值比较可知,由Archard磨损公式建立了球阀磨损线性函数能反映球阀磨损的情况,计算值和仿真值趋势一致,结果相近;

(2) 球阀结构和工作参数对磨损可靠度不是简单的单调线性关系,各参数在一定区间范围内球阀可靠度较高,球阀可按照一定规律进行前期优化设计和后期合理使用.